基本不等式與其他知識的交匯融合

丁建兵

?江蘇省西亭高級中學

本文中歸納總結了基本不等式與其他知識交匯融合的6種常見題型，并結合具體實例進行分析求解，以引導學生通過總結歸納強化和提升對相關知識、方法的綜合運用能力.

1 常見題型一：基本不等式與函數的交匯

求解有關代數式的范圍或最值時，往往需要適當構造函數，在數形結合的基礎上，利用基本不等式或者基本不等式的變形結論加以靈活求解.

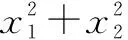
C.(2,+∞) D.(0,1)

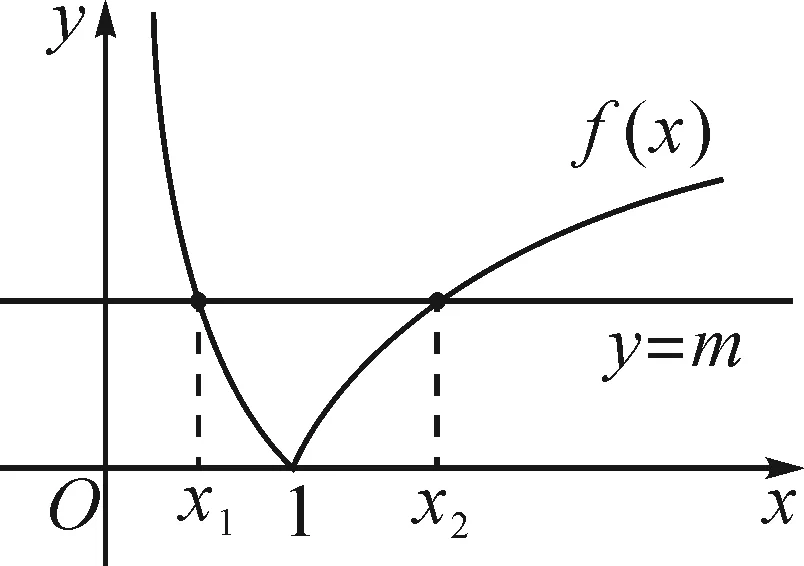
圖1

解析：如圖1，在同一坐標系中分別畫出函數f(x)=|lnx|的圖象與直線y=m.根據題意可知函數y=|lnx|的圖象與直線y=m有兩個不同的交點，且交點的橫坐標分別為x1和x2，不妨設x11.

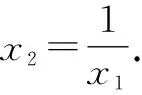
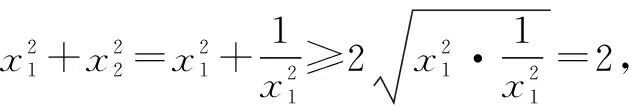
故選：C.

評注：本題求解的關鍵有三點.一是活用數形結合思想轉化題設已知條件；二是根據方程的根，獲得x1x2=1；三是借助基本不等式，準確求解目標式的取值范圍.

2 常見題型二：基本不等式與數列的交匯

以數列知識為背景而設置的求解最值問題，需要先根據等差數列、等比數列知識進行具體分析，以便適當轉化目標式(寫成一元代數式)，再靈活運用基本不等式即可順利獲解.

例2已知遞增等差數列{an}中，a1a2=-2，則a3的( ).

A.最大值為-4 B.最小值為4

C.最小值為-4 D.最大值為4或-4

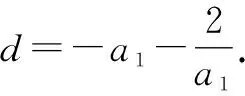
故選：B.

評注：本題看似簡單，但實則考查了等差數列的通項公式、單調性與基本不等式在求解最值問題中的綜合運用，且求最值時極易出錯(沒有關注基本不等式成立的前提條件).

3 常見題型三：基本不等式與向量的交匯

處理平面向量中的有關最值問題時，往往需要在數形結合的基礎上，先根據平面向量知識分析獲得一個具體的結論，再利用該結論以及基本不等式靈活求解目標式的最值問題.

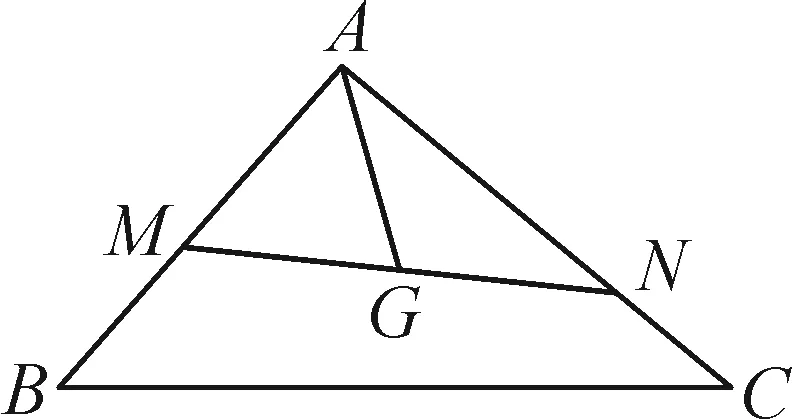
圖2

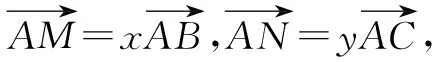
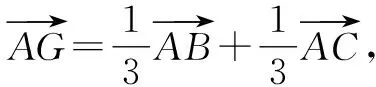
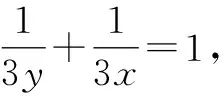
評注：本題主要考查了基底向量與向量的共線定理、性質在解題中的綜合運用，同時也考查了利用基本不等式巧求目標代數式的最小值(需要借助“1”的特性靈活變形).

4 常見題型四：基本不等式與直線和圓的交匯

處理直線和圓中的有關取值范圍問題時，需要先根據直線與圓的位置關系進行分析獲得一個具體的結論，再借助基本不等式或者基本不等式的推廣性結論加以靈活求解.

例4設m,n∈R，若直線(m+1)x+(n+1)y-2=0與圓(x-1)2+(y-1)2=1相切，則m+n的取值范圍是( ).

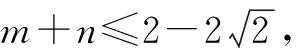
故選：D.

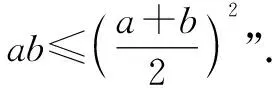
5 常見題型五：基本不等式與立體幾何的交匯

以立體幾何為背景而設置的最值求解問題，需要先根據空間圖形以及立體幾何相關知識進行具體分析，進而靈活運用基本不等式即可順利獲解.

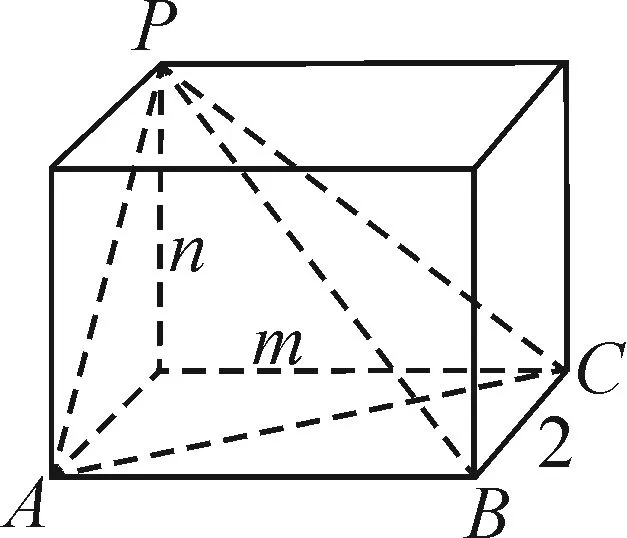
圖3

例5如圖3，三棱錐P-ABC的四個頂點恰是長、寬、高分別是m,2,n的長方體的頂點，若此三棱錐的體積為2，則該三棱錐外接球體積的最小值為.

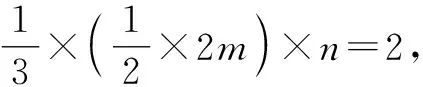
評注：本題主要考查了三棱錐的體積公式、球的體積公式以及基本不等式在解題中的綜合運用，有利于較好地培養學生的空間想象能力以及數形結合能力.

6 常見題型六：基本不等式與解三角形的交匯

處理解三角形中的有關最值問題時，往往需要先根據正弦定理、余弦定理、面積公式以及相關三角函數知識進行綜合分析，再靈活運用基本不等式即可順利獲解.

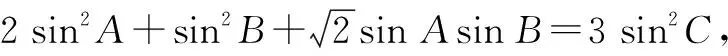
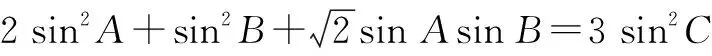
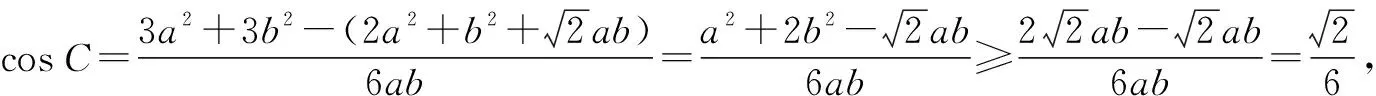
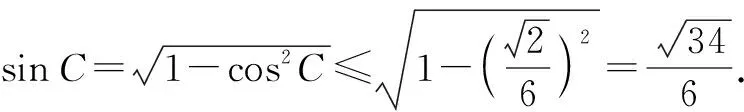
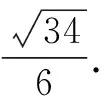
評注：本題主要考查了正弦定理、余弦定理以及基本不等式在解題中的綜合運用，有利于較好地培養學生數學運算、邏輯推理等核心素養.

總之，在處理有關范圍或最值問題時，應適時創造有利條件，以便靈活運用基本不等式獲得巧思妙解，進而提高解題的技能技巧，且學且悟且提升！