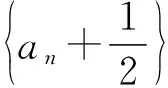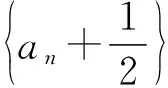例談高中數學化歸與轉化思想的常見處理策略

劉光明

(廣東省華南師范大學附屬中學汕尾學校)

數學家喬治·波利亞說:“掌握數學就是意味著善于解題”.這就是說善于解題,不僅善于解一些標準的題,而且善于解一些要求獨立思考、思路合理、見解獨到和有發現創造的題.新高考新教材背景下的數學更加強調“減少機械刷題”,注重通性通法,這意味著數學問題解決的方向是“化歸”,將復雜的問題簡單化、抽象的問題具體化、未知的問題已知化.

轉化思想在狹義上稱為化歸思想,通常有數形轉化、構造轉化、聯想轉化及類比轉化等不同形式.轉化的過程需要遵循簡單化、熟悉化、直觀化、和諧化、正難則反等原則.下面通過近幾年高考真題或者新教材習題等實例闡述常見的化歸策略.

策略一 建系,將幾何轉化為代數

建立平面直角坐標系或者空間直角坐標系能夠將幾何元素轉化為坐標表示,通過代數運算和邏輯推理處理問題.尤其是解三角形、向量、立體幾何、解析幾何等相關問題,建系常常能起到事半功倍的效果.

【解析】如圖,建立平面直角坐標系xOy,

設BD=t(t>0),則CD=2t.

又∠ADB=120°,AD=2,

【評注】建立平面直角坐標系,將三角形中的線段長轉化為兩點間的距離問題,經過代數變形聯想到利用基本不等式求最值,有效避免了解三角形的復雜三角函數運算,體現了數學的簡潔美.建系處理三角形問題是解三角形中比較常見的思維路徑,解三角難題需常聯想到它.

【解析】解法一:以點B為坐標原點,BC所在直線為x軸建立如圖所示的平面直角坐標系xBy.

∵BC=6,

∴C(6,0).

又∵AB=3,∠ABC=60°,

設M(x,0),則N(x+1,0)(其中0≤x≤5),

解法二:如圖,取MN的中點F,連接DF,

因此當DF⊥MN時,DF取最小值,

【評注】解法一,建立平面直角坐標系,將內積問題轉化為坐標運算,是解決向量問題的常見思路.解法二,在△DMN中,取MN的中點F,聯想極化恒等式模型,將內積轉化為線段的長度,借助平行線間垂線段最短這一幾何結論巧妙化解難點.

【例題3】(2021·全國甲卷理·19)如圖,已知直三棱柱ABC-A1B1C1中,側面AA1B1B為正方形,AB=BC=2,E,F分別為AC和CC1的中點,D為棱A1B1上的點,BF⊥A1B1.

(Ⅰ)證明:BF⊥DE;

(Ⅱ)當B1D為何值時,面BB1C1C與面DFE所成的二面角的正弦值最小?

【解析】(Ⅰ)證明:∵三棱柱ABC-A1B1C1是直三棱柱,

∴BB1⊥底面ABC.

又∵AB,BC?平面ABC,

∴BB1⊥AB,BB1⊥BC.

∵A1B1∥AB,BF⊥A1B1,

∴BF⊥AB.

又BB1∩BF=B,BB1,BF?平面BCC1B1,

∴AB⊥平面BCC1B1,

故AB⊥BC,AB⊥BB1.

以B為坐標原點,BA,BC,BB1所在直線分別為x,y,z軸建立如圖所示的空間直角坐標系,

則B(0,0,0),A(2,0,0),B1(0,0,2),E(1,1,0),F(0,2,1).

設D(a,0,2)(0≤a≤2).

∴BF⊥DE.

(Ⅱ)設平面DFE的法向量為m=(x,y,z),

令z=2-a,

則m=(3,1+a,2-a).

設平面BB1C1C與平面DFE的二面角的平面角為θ,

【評注】立體幾何中平行、垂直、夾角及距離等幾何問題,采取綜合幾何法解決時對邏輯推理的要求較高,而借助空間直角坐標系轉化為相應的代數運算,將最值問題轉化為函數問題,以運算推導分化定理的邏輯推理難度.空間向量的引入是解決立體幾何問題的一種革命.

策略二 構圖,將抽象轉化為直觀

處理數學問題,通常可從代數、幾何等不同的角度去剖析問題,以形助數、以數解形,通過改變問題的內部或外部結構特征,實施有效的化歸與轉化,將抽象問題直觀化,基于顯性特征,運用邏輯推理解決問題.

【解析】當x∈(0,2]時,

即(x-1)2+y2=1,y≥0.

又f(x)為奇函數,周期為4,

如圖,畫出函數f(x)與g(x)的大致圖象,

要使f(x)=g(x)在(0,9]上有8個實根,

只需兩個函數圖象有8個交點即可.

函數f(x)與g(x)的圖象有2個交點;

當g(x)=k(x+2)時,

g(x)為恒過點(-2,0)的直線,

只需函數f(x)與g(x)=k(x+2)的圖象有6個交點.

當f(x)與g(x)圖象相切時,

點(1,0)到直線kx-y+2k=0的距離為1,

此時函數f(x)與g(x)的圖象恰有3個交點;

當g(x)=k(x+2)過點(1,1)時,

函數f(x)與g(x)的圖象有6個交點,

【評注】根據函數的周期性作圖,將方程的根的個數轉化為兩個函數圖象的交點個數問題,通過數形結合,從而確定參數的取值范圍.函數零點問題,通過數形結合能夠將問題轉化為直觀的圖形分析,化繁為簡,簡潔明了.

( )

作出函數g(t)=sint的大致圖象如圖所示.

又f(x)在(0,π)上有三個極值點、兩個零點,

故選C.

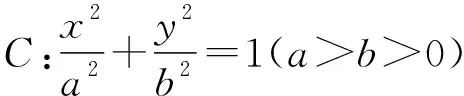
【解析】如圖,過點P作PM⊥AF2的延長線,

垂足為M,

因為△PF1F2為等腰三角形,

F1F2=2c,∠F1F2P=120°,

所以PF2=2c,∠PF2M=60°,

所以在Rt△PAM中,

【評注】解析幾何如果僅僅是純粹的代數計算那便失去了幾何的味道,故解析幾何問題首先要仔細分析幾何關系,構造幾何圖形,將問題轉化為幾何關系.理清幾何關系,明確運算方向,優化運算,實現少算多想.

策略三 換元,將復雜轉化為簡單

【解析】如圖,以A為坐標原點,

AD所在直線為x軸,AB所在直線為y軸建立平面直角坐標系,

則點C坐標為(2,1).

因為|AB|=1,|AD|=2,

又BD是⊙C的切線,切點為E,

所以CE⊥BD,

因為P在⊙C上,

則λ+μ的最大值為3.

令2ax2-x+1=0,

方程2ax2-x+1=0有兩個不相等的正根x1,x2,

不妨設x1

當x∈(0,x1)∪(x2,+∞)時,f′(x)<0,

當x∈(x1,x2)時,f′(x)>0,

故函數f(x)在(0,x1),(x2,+∞)上單調遞減,在(x1,x2)上單調遞增,

即f(x)有極小值點x1和極大值點x2,

故f(x1)+f(x2)>5-2ln2.

(Ⅰ)討論f(x)的單調性;

當a≤2時,f(x)在(0,+∞)上單調遞減;

(Ⅱ)證明:由(Ⅰ)知,當且僅當a>2時,f(x)存在兩個極值點.

由于f(x)的兩個極值點x1,x2滿足x2-ax+1=0,

所以x1x2=1,

不妨設x11.

由(Ⅰ)知,g(x)在(0,+∞)上單調遞減,

又g(1)=0,從而當x∈(1,+∞)時,g(x)<0,

【評注】多變量問題常規做法都是通過換元或者消元將多變量問題轉化為單變量問題進行處理.例題8充分借助韋達定理,將和與乘積進行整體換元,例題9充分利用兩個變量的等量關系x1x2=1實現用一個變量表示另一個變量,將二元問題轉化為單變量問題,并轉化為單變量函數問題,然后構造函數解決問題.

【例題10】(2015·全國Ⅰ卷文·21)設函數f(x)=e2x-alnx.

(Ⅰ)討論f(x)的導函數f′(x)的零點的個數;

【解析】(Ⅰ)f(x)的定義域為(0,+∞),

當a≤0時,f′(x)>0,f′(x)沒有零點;

當a>0時,f′(x)在(0,+∞)上單調遞增.

f′(b)<0,

故當a>0時,f′(x)存在唯一零點.

(Ⅱ)證明:由(Ⅰ)可設f′(x)在(0,+∞)上的唯一零點為x0,

當x∈(0,x0)時,f′(x)<0;

當x∈(x0,+∞)時,f′(x)>0,

故f(x)在(0,x0)上單調遞減,

在(x0,+∞)上單調遞增,

所以當x=x0時,

f(x)取得最小值,

最小值為f(x0)=e2x0-alnx0.

故當a>0時,

【評注】例題10第(Ⅱ)題極小值存在但不可直接求出,故假設極小值點x0,將最小值轉化為x0的代數式,再將指數式和對數式用多項式進行換元,轉化為基本不等式模型求解取值范圍.與“隱零點”問題類似,通常都要涉及設元,將超越式或者復雜式子通過換元轉化為多項式函數問題進行處理.

策略四 構造,將陌生轉化為熟悉

【例題11】已知數列{an}滿足a1=1,an+1=3an+1.

【證明】(Ⅰ)由an+1=3an+1得

因為當n≥1時,3n-1≥2·3n-1,

( )

A.a

C.c

【解析】設f(x)=ln(1+x)-x,x>-1,

當x∈(-1,0)時,f′(x)>0,

當x∈(0,+∞)時,f′(x)<0,

所以函數f(x)在(0,+∞)上單調遞減,

在(-1,0)上單調遞增,

故a

設g(x)=xex+ln(1-x),0

令h(x)=ex(x2-1)+1,0

則h′(x)=ex(x2+2x-1),

則函數h(x)=ex(x2-1)+1單調遞減;

則函數h(x)=ex(x2-1)+1單調遞增.

又h(0)=0,

即g′(x)>0,

所以函數g(x)單調遞增,

所以g(0.1)>g(0)=0,

即0.1e0.1>-ln0.9,

所以a>c,故c

【評注】比較大小問題是近幾年全國卷的熱點問題,本題難度較大,需要構造函數借助函數的單調性將實數大小轉化為函數值的大小.根據代數結構特征構造函數需要平時積累一定的基本活動經驗,敢于嘗試,大膽創新.

策略五 分類討論,將未知轉化為已知

當a≤0時,ax-1<0,

當x∈(0,1)時,f′(x)>0,f(x)單調遞增;

當x∈(1,+∞)時,f′(x)<0,f(x)單調遞減,

故f(x)max=f(1)=a-1<0,

此時函數無零點,不符合題意;

又f(1)=a-1<0,

所以f(x)單調遞增.

又f(1)=a-1=0,

所以f(x)有唯一零點,符合題意;

此時f(1)=a-1>0.

使得f(n)<0,

所以f(x)有唯一零點,符合題意.

綜上所述,a的取值范圍為(0,+∞).

【評注】解決本題的關鍵是利用導數研究函數的單調性與極值,通過對參數取值范圍的分類討論,把函數零點問題轉化為函數的單調性與極值的問題.參數的取值范圍確定了,就相當于多了一個已知條件,原來模糊的取值就變得明晰了.

【教學建議】