靈活應用平行四邊形的性質與判定
劉丹丹
沈陽市博才初級中學邵愛平老師的直播課《平行四邊形性質與判定綜合應用》選自遼寧教育學院“學到匯”公眾服務平臺“遼寧省初中數學學科周末名師公益課堂”,旨在貫徹落實國家“雙減”政策,幫助廣大師生自主學習和個性化提升。
邵愛平老師的直播課,從知識梳理、典型例題、變式訓練、中考鏈接四個方面展開,幫助同學們結合圖形理解、總結平行四邊形的性質及判定方法,引導同學們多角度思考,發現最優方法. 平行四邊形是初中數學“圖形與幾何”領域的重要圖形之一. 它既是平行線、全等三角形等知識的后續應用,又是進一步理解特殊平行四邊形(矩形、菱形、正方形)的必要基礎,為研究兩條直線平行、線段相等及角相等提供了新的方法和依據.
典例探究
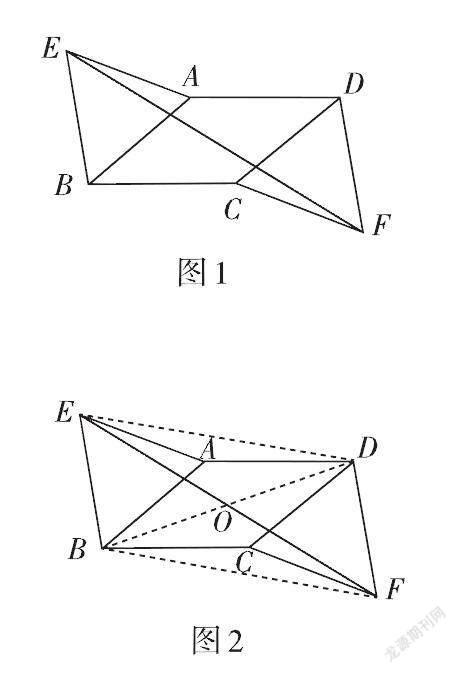
例 如圖1,在?ABCD中,以AB,CD為邊在?ABCD外側作等邊三角形AEB和等邊三角形CFD.求證:四邊形EBFD是平行四邊形.
學法指導1:從邊的角度證明平行四邊形,兼顧邊的數量和位置關系,根據“一組對邊平行且相等的四邊形是平行四邊形”求證結論.
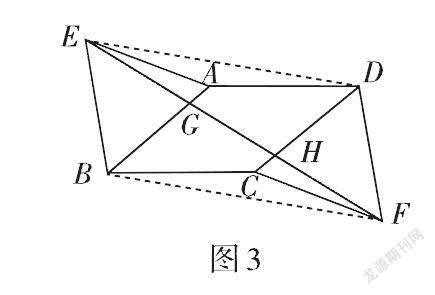
證法1:如圖2,連接ED,BF,BD,BD與EF交于點O,
∵四邊形ABCD為平行四邊形,
∴AB = CD,AB[?]CD,∴∠ABD = ∠CDB.
∵△AEB,△CFD均為等邊三角形,
∴BE = AB = CD = DF,∠EBA = ∠CDF = 60°,
∴∠ABD + ∠EBA = ∠CDB + ∠CDF,即∠EBO = ∠FDO,
∴BE[?]DF.
∵BE[?]DF,BE = DF,∴四邊形EBFD是平行四邊形.
學法指導2:從邊的角度證明平行四邊形,如果只考慮邊的數量關系,需要根據“兩組對邊分別相等”求證結論.
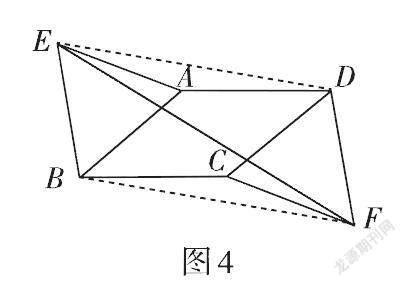
證法2:如圖3,設AB,CD與EF分別交于點G,H,連接ED,BF,
∵四邊形ABCD為平行四邊形,
∴AB[?]CD,AB = CD,∴∠AGH = ∠CHG.
∵∠BGE = ∠AGH,∠DHF = ∠CHG,
∴∠BGE = ∠DHF.
∵△AEB,△CFD均為等邊三角形,
∴BE = AB = CD = DF,∠EBA = ∠CDF = 60°.
∵∠BEG = 180° - ∠EBA - ∠BGE,∠DFH = 180° - ∠CDF - ∠DHF,
∴∠BEG = ∠DFH,∴BE[?]DF.
∵BE = DF,∴四邊形EBFD是平行四邊形.
學法指導3:從邊的角度證明平行四邊形,如果只考慮邊的位置關系,需要根據“兩組對邊分別平行”來證明.
證法3:連接DE,BF,
∵四邊形ABCD為平行四邊形,
∴AD = BC,AD[?]BC,∠BAD = ∠BCD.
∵△AEB,△CFD均為等邊三角形,
∴BE = AE = AB = CD = CF = DF,∠EAB = ∠DCF = 60°.
∵∠EAD = 360° - ∠EAB - ∠BAD,∠FCB = 360° - ∠DCF - ∠BCD,
∴∠EAD = ∠FCB.
∵AE = CF,AD = BC,∴△ADE ≌ △CBF,∴DE = BF.
∵BE = DF,DE = BF,∴四邊形EBFD是平行四邊形.
學法指導4:從特殊線的角度證明平行四邊形,需要根據“對角線互相平分的四邊形是平行四邊形”來證明.
思考:你能類比上面的推理思路和過程,得到其他證法嗎?你認為哪種證明思路更簡捷?
分層作業
難度系數:★★★ 解題時間:4分鐘
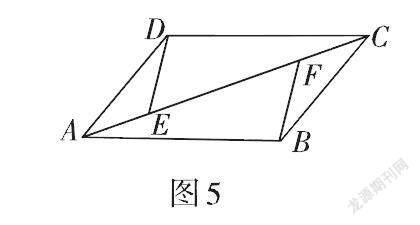
四邊形ABCD為平行四邊形,連接AC,點E,F在AC上,且AE = CF,求證:四邊形DEBF為平行四邊形.(請同學們從多角度思考,答案略)
〔作者單位:遼寧省實驗中學(初中部)〕

