基于“三線”的高考試題賞析與改編
成樹明
(山東省濱州市第一中學)
高考評價體系是物理高考命題的根本指南,也是一線高中教師指導學生備考的綱領性文件。高考評價體系在高考命題實踐中最為明顯的特征是三線貫通:“核心價值金線”是一份試卷的靈魂,“能力素養銀線”是一份試卷的骨骼,“情境載體串聯線”是一份試卷的形體。“無價值,不入題” “無思維,不命題” “無情境,不成題”已成為高考命題的主要特征。
近幾年的高考物理試題是在高考評價體系理論指導下,由命題專家集體打磨出的智慧結晶,既考查了高中物理的必備知識和關鍵能力,也注重了物理思想和方法的考查,是高三物理教學和備考的好素材。對高考物理試題進行變式訓練,做到一題多變,多題歸一,是培養學生模型建構、邏輯推理與批判性思維等高階思維的有效途徑。一線教師在對高考試題進行改編和模擬題的命制過程中,也要以高考評價體系為依據,努力落實好“三線貫通”。
1 基于生活實踐情境的高考試題賞析與改編
1.1 原題呈現
【例1】(2021·廣東卷·13)算盤是我國古老的計算工具,中心帶孔的相同算珠可在算盤的固定導桿上滑動,使用前算珠需要歸零,如圖1所示,水平放置的算盤中有甲、乙兩顆算珠未在歸零位置,甲靠邊框b,甲、乙相隔s1=3.5×10-2m,乙與邊框a相隔s2=2.0×10-2m,算珠與導桿間的動摩擦因數μ=0.1。現用手指將甲以0.4 m/s的初速度撥出,甲、乙碰撞后甲的速度大小為0.1 m/s,方向不變,碰撞時間極短且不計,重力加速度g取10 m/s2。

圖1
(1)通過計算,判斷乙算珠能否滑動到邊框a;
(2)求甲算珠從撥出到停下所需的時間。
【解析】(1)設甲、乙算珠的質量為m,滑動時由牛頓第二定律,得
μmg=ma
設甲珠與乙珠碰前速度為v1,從甲珠以v0=0.4 m/s的初速度撥出到與乙珠碰撞前,由運動學公式,得
由題意知碰撞后甲珠的速度為
v2=0.1 m/s
設碰撞后乙珠的速度為v3,甲、乙碰撞時由動量守恒定律得
mv1=mv2+mv3
碰撞后乙珠做勻減速直線運動,設乙珠速度減為零時的位移為x,由運動學公式,得
聯立解得x=0.02 m
因x=s2,故乙珠恰好運動到邊框a
(2)設甲珠與乙珠碰前運動時間為t1,由運動學公式,得
v1=v0-at1
設碰撞后甲珠運動時間為t2,由運動學公式,得
0=v2-at2
則甲運動的總時間為
t=t1+t2
聯立解得t=0.2 s
1.2 試題賞析
題目以中華傳統文化中的算盤為生活實踐情境進行命制,考查多物體、多過程問題。本題在落實“三線”的基礎上,重點突出了“核心價值金線”的考查。“核心價值金線”主要是圍繞立德樹人來考查學生的政治立場和思維觀念、世界觀和方法論以及道德品質。愛國主義情懷、世界觀和方法論、科學精神這三個方面構建起物理學科具體的“核心價值金線”。近幾年高考物理試題,常以我國的重大科技成果、航天巨大成就等為情境,展示我國科技日新月異的進步,激發學生的進取意識、實現中國夢的使命感和責任感。也常以中國古代科技和物理學史為情境,感受我國古代發達的科學技術、弘揚中華優秀傳統文化,激發民族自豪感,厚植愛國主義情感。通過分析解答近幾年的高考物理試題,有助于學生形成科學的世界觀和正確的方法論,有助于培養學生實事求是、求真務實、開拓創新的科學精神。
1.3 試題改編
【改編1】某冰壺隊為了迎接北京冬奧會,積極開展訓練。某次訓練中使用的紅色冰壺A和藍色冰壺B質量均為20 kg,開始兩壺之間的距離為s=7.5 m,運動員以v0=2 m/s初速度將紅色冰壺A擲出,與靜止的藍色冰壺B碰撞后紅色冰壺A的速度大小為vA=0.2 m/s,方向不變,碰撞時間極短且不計。已知兩冰壺與冰面間的動摩擦因數均為μ=0.02,重力加速度g取10 m/s2。求:
(1)紅色冰壺A從開始運動到停下所需的時間;
(2)兩冰壺碰撞過程中損失的機械能。
【解析】(1)兩冰壺在冰面上滑動時,由牛頓第二定律,得
μmg=ma
設紅色冰壺A與藍色冰壺B碰前的速度v,由運動學公式,得
v=v0-at1
0=vA-at2
紅色冰壺A運動的總時間為
t=t1+t2
聯立解得t=6 s
(2)碰撞過程,由動量守恒定律和能量守恒定律,得
mv=mvA+mvB
聯立解得ΔE=3.2 J
【改編2】(多選)2022年2月4日北京冬奧會開幕,冰壺是冬奧會的傳統比賽項目。如圖2所示,某次比賽中運動員將紅色冰壺A擲出,與靜止的藍色冰壺B碰撞,碰撞后兩冰壺的v-t圖像如圖3所示。已知重力加速度g為10 m/s2,下列說法正確的是

圖2
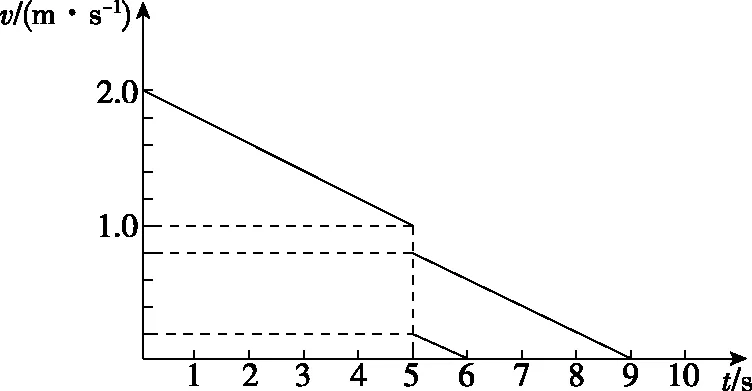
圖3
( )
A.紅色冰壺A與冰面的動摩擦因數為0.2
B.藍色冰壺B與冰面的動摩擦因數為0.02
C.開始紅藍兩冰壺之間的距離為7.5 m
D.碰后紅色冰壺A運動的距離為1.6 m
【答案】BC

1.4 改編小結
以北京冬奧會這一重大歷史事件和冰壺體育運動為情境進行改編和命制,仍突出了“核心價值金線”的考查,通過北京冬奧會的舉辦,使學生進一步感受到了體育精神和奧林匹克精神,進一步增強了民族自豪感和對國家未來的信心。改編1是通過情境設置與設問角度的改變進行的創作,這是試題改編常用的兩種技術。由算盤改為北京冬奧會,由兩個算珠改為兩個冰壺,都是一個運動的物體去碰一個靜止的物體,碰后都做勻減速直線運動,兩題的本質是一樣的。學生通過對兩題的解答,可以透過現象看本質,提升模型建構能力,有利于高階思維的養成;改編2是由改編1將文本信息改編為圖像信息,并由計算題改編成選擇題進行的創作,從而將試題難度也進行了降低。文本信息與圖表信息的相互轉換,計算題與選擇題兩種題型的相互轉換,都是試題改編的常用技術。
2 基于學習探索情境的高考試題賞析與改編
2.1 原題呈現
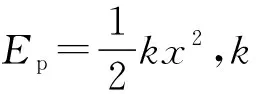
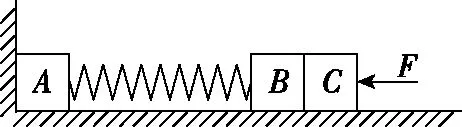
圖4
(1)求B、C向左移動的最大距離x0和B、C分離時B的動能Ek;
(2)為保證A能離開墻壁,求恒力的最小值Fmin;
(3)若三物塊都停止時B、C間的距離為xBC,從B、C分離到B停止運動的整個過程,B克服彈簧彈力做的功為W,通過推導比較W與fxBC的大小;
(4)若F=5f,請在圖5所給坐標系中,畫出C向右運動過程中加速度a隨位移x變化的圖像,并在坐標軸上標出開始運動和停止運動時的a、x值(用f、k、m表示),不要求推導過程。以撤去F時C的位置為坐標原點,水平向右為正方向。

圖5
【解析】(1)從開始到B、C向左移動到最大距離的過程中,以B、C和彈簧為研究對象,由功能關系得
彈簧恢復原長時B、C分離,從彈簧最短到B、C分離,以B、C和彈簧為研究對象,由能量守恒定律得
聯立方程解得
(2)當A剛要離開墻時,設彈簧的伸長量為x,以A為研究對象,由平衡條件得
kx=f
若A剛要離開墻壁時B的速度恰好等于零,這種情況下恒力為最小值Fmin,從彈簧恢復原長到A剛要離開墻的過程中,以B和彈簧為研究對象,由能量守恒定律得
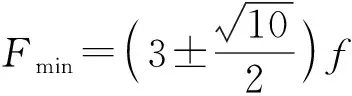
(3)從B、C分離到B停止運動,設B的路程為xB,C的位移為xC,以B為研究對象,由動能定理得
-W-fxB=0-Ek
以C為研究對象,由動能定理得
-fxC=0-Ek
由B、C的運動關系得
xB>xC-xBC
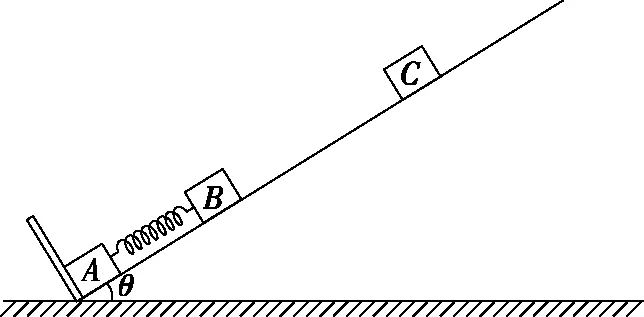
聯立解得W (4)小物塊B、C向左運動過程中,由動能定理得 解得撤去恒力瞬間彈簧彈力為 kx1=6f 則坐標原點的加速度為 之后C開始向右運動過程(B、C系統未脫離彈簧)加速度為 可知加速度隨位移x為線性關系,隨著彈簧逐漸恢復原長,x減小,a減小,彈簧恢復原長時,B和C分離,之后C只受地面的滑動摩擦力,加速度為 負號表示C的加速度方向水平向左;從撤去恒力之后到彈簧恢復原長,以B、C為研究對象,由動能定理得 脫離彈簧瞬間后C速度為v,之后C受到滑動摩擦力減速至0,由能量守恒定律得 解得脫離彈簧后,C運動的距離為 則C最后停止的位移為 所以C向右運動的a-x圖像如圖6所示 圖6 題目以常見的物塊和彈簧為學習探索情境進行命制,考查了多物體、多過程問題。本題在落實“三線”的基礎上,重點突出了“能力素養銀線”的考查。物理觀念、科學思維、科學探究、科學態度與責任為物理學科的學科素養。本題考查了物理觀念中的物質觀念、運動與相互作用觀念、能量觀念等;解答本題需要運用抽象與聯想、模型與建模、推演與計算等思維方法。本題還考查了考生的理解能力、模型建構能力、邏輯推理能力、分析綜合能力、信息加工能力等,這些都是物理學科的關鍵能力。 圖7 (1)求小物塊A、B碰后瞬時速度的大小; (2)求小物塊B向下運動的最大位移; (3)小物塊B向下運動至最低點時,求小物塊C對水平面壓力的大小; (4)若小物塊B向上運動到最高點時,小物塊C恰好離開地面,求小物塊A開始下落時距小物塊B的高度。 【解析】(1)小物塊A下落過程,由動能定理得 小物塊A、B碰撞過程,由動量守恒定律得 mv1=2mv2 解得小物塊A、B碰后瞬時速度的大小為 (2)設彈簧開始時的壓縮量為x0,則 mg=kx0 設小物塊A、B一起運動到最低點的過程中發生的位移大小為x,由能量守恒定律得 (3)小物塊B向下運動至最低點時,以小物塊C為研究對象,由受力平衡得 FN=mg+k(x0+x) 由牛頓第三定律知小物塊C對水平面壓力的大小為 (4)小物塊C為研究對象,有 mg=kx1 設此時小物塊A開始下落時距小物塊B的高度為H,下落過程與碰撞過程有 mv3=2mv4 小物塊A、B在彈簧原長處分離,設分離時的速度大小為v5,由能量守恒定律得 小物塊A、B分離后,小物塊B向上運動到最高點的過程中,由能量守恒定律得 圖8 (1)求小物塊B碰后瞬時速度的大小; (2)求小物塊B向下運動的最大位移; (3)小物塊B向下運動至最低點時,求小物塊A對擋板的壓力大小; (4)若小物塊B沿斜面向上運動到最高點時,小物塊A恰好離開擋板,求小物塊C開始下落時距小物塊B的距離。 【解析】(1)小物塊C下落過程,由動能定理得 小物塊B、C碰撞過程,由動量守恒定律得 mv1=2mv2 解得小物塊B碰后瞬時速度的大小為 (2)設彈簧開始時的壓縮量為x0,則 mgsinθ=kx0 設小物塊B、C一起運動到最低點的過程中發生的位移大小為x,由能量守恒定律得 (3)小物塊B向下運動至最低點時,以小物塊A為研究對象,由受力平衡得 FN=mgsinθ+k(x0+x) 聯立解得 由牛頓第三定律知小物塊A對擋板的壓力大小為 (4)以小物塊A為研究對象,有 mgsinθ=kx1 解得x1=x0=2Lsinθ 設小物塊C開始運動時距小物塊B的距離為L0,下落過程與碰撞過程有 mv3=2mv4 小物塊B、C在彈簧原長處分離,設分離時的速度大小為v5,由能量守恒定律得 小物塊B、C分離后,小物塊B向上運動到最高點的過程中,由能量守恒定律得 聯立解得L0=18Lsinθ 改編題情境與原題相同,改編方法是進行的空間轉換,原題三個小物塊及彈簧水平放置,改編1題將三個小物塊及彈簧豎直放置,改編2題是將三個小物塊及彈簧沿斜面放置。相同點都是兩小物塊與彈簧相連,另一小物塊在恒力作用下運動,不同點改編題開始運動的小物塊的重力不能撤去。改編題與原題的設問角度也不相同,但都突出了“能力素養銀線”的考查。 高考試題是理解和把握高考評價體系的重要載體,也是進行高中物理教學的好素材。教師對高考試題的研究和解讀,要依據高考評價體系,善于從三線的角度去分析和研究,從而選擇恰當的高考試題用于教學的不同階段,在高三教學和備考中更要精選高考試題。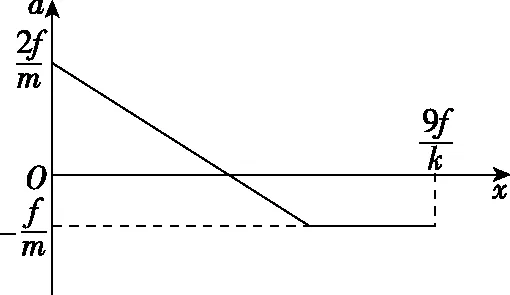
2.2 試題賞析
2.3 試題改編


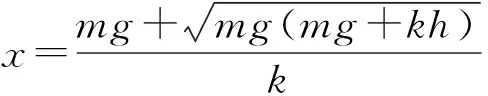
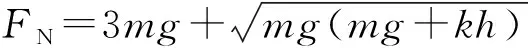


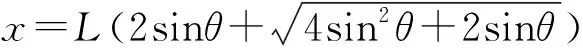
2.4 改編小結
3 教學啟示
3.1 加強高考試題研究
3.2 提升教師命題能力


