基于開源數字仿真軟件Digital的“數字邏輯”及“計算機組成原理”課程實驗設計

邢建國

摘要：本文介紹了一款開源數字電路仿真軟件Digital在數字邏輯和計算機組成等課程實驗中的應用，并呈現出四個不同復雜度的組合和時序電路的設計與實現。實踐表明，該軟件適合于計算機類專業學生學習和掌握諸如處理器一類復雜數字系統設計。

關鍵詞：數字邏輯；計算機組成；Digital; 實驗設計

中圖分類號：G434? 文獻標識碼：A? 論文編號：1674-2117（2023）08-0095-06

前言

開源軟件Logisim數字仿真軟件是由Carl Burch開發的一款開源、免費的數字系統仿真軟件。筆者所在學校用該軟件重構了已有的大部分實驗，很多學生利用該軟件設計的系統也達到了實驗要求。但在教學過程中筆者發現，Logisim無法直接使用Verilog模塊，這對一些復雜模塊如狀態機、浮點運算器來說實現起來不方便，也難以調試。由Helmut Neemann開發的開源軟件Digital則針對Logisim存在的一些問題重新進行了設計，并在底層架構上做了重大調整，增加了很多新的特色功能，比Logisim更適合于復雜數字系統的仿真實現，其主要特點包括：①支持與、或、非等基本邏輯模塊，以及一些輸入輸出設備、計算、存儲等復雜模塊。②支持真值表、卡諾圖、邏輯表達式以及狀態機的電路綜合。③支持波形顯示，提供了測試用例（實際上提供了一種編寫測試用例的小語言）。④支持Telent協議，外部應用可以與設計的電路系統進行通信，這為調試圖像處理器的復雜系統提供了較大的便利。⑤可以將Verilog和VHDL編寫的模塊集成到設計的電路中（這些模塊的仿真是通過Icarus Verilog和ghdl外部模擬器來實現的），也可以把設計的系統導出為Verilog和VHDL文件。

下面，筆者將通過具體的教學案例來說明該軟件在數字邏輯、計算機組成等課程中的實際應用。案例包括超前進位加法器（組合邏輯）、最大公因子GCD電路（有限狀態自動機）、階乘Factorial電路（下推自動機）以及一個8指令處理器BrainFxxK（圖靈機）的實現。

設計案例

1.組合電路設計：超前進位加法器

加法是算術邏輯單元中的重要組件。最簡單的加法器是由多個1位全加器串聯起來的串行進位加法器。由于進位延遲大，該加法器速度與位數成反比。因此，實踐中一般采用超前進位加法器，其基本思路是用專門的電路來并行計算出進位。對于一個n位加法：

{cout， sum} = a + b + cin

其第i+1位的進位邏輯表達式為：

c[i+1] = a[i] b[i] + （a[i] + b[i]） c[i]

其中a[i] b[i]為生成項，記為g[i]，a[i] + b[i]為傳播項，記為p[i]。則c[i+1]可以表示為：

c[i+1] = g[i] + p[i] c[i]

= g[i] + p[i] g[i-1] + p[i] p[i-1] g[i-2] + ... + p[i] p[i-1]...p[1] p[0]cin

可以使用樹形結構分層產生進位。為此筆者設計了gp模塊，其功能是根據輸入的兩個加法器的g0、p0和g1、p1以及低位進位cin生成g、p和cout，其邏輯表達式為：

g = g1 | （p1 & g0）

p = p1 & p0

cout = g0 | （p0 & cin）

1位加法器模塊為：

sum = a ^ b ^ cin

g = a & b

p = a | b

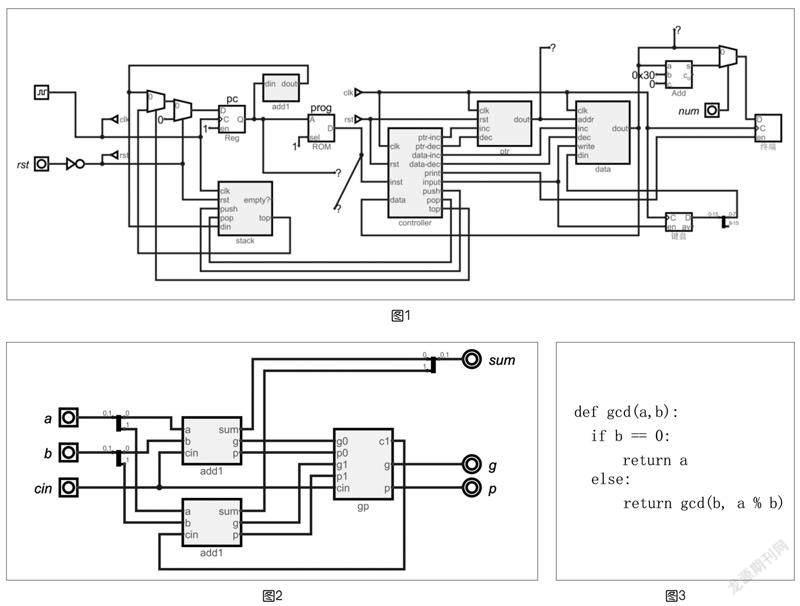
其在Ditigal中分別實現如圖1所示。

可以使用2個1位加法器和1個gp構造一個2位加法器，如圖2所示。

同樣，可以使用2個2位加法器和1個gp構造1個4位加法器以及更多位數的加法器。

通過這個例子，可以發現Ditigal對一些簡單的組合邏輯可以很方便進行抽象、重用，由此可以構造更復雜的系統。

2.有限狀態自動機設計：最大公因子（gcd）

本案例是展示如何使用Digital的Verilog模塊來簡化狀態機的實現。該例子用歐幾里算法來計算兩個正整數的最大公因子。該算法的Python實現如上頁圖3所示。

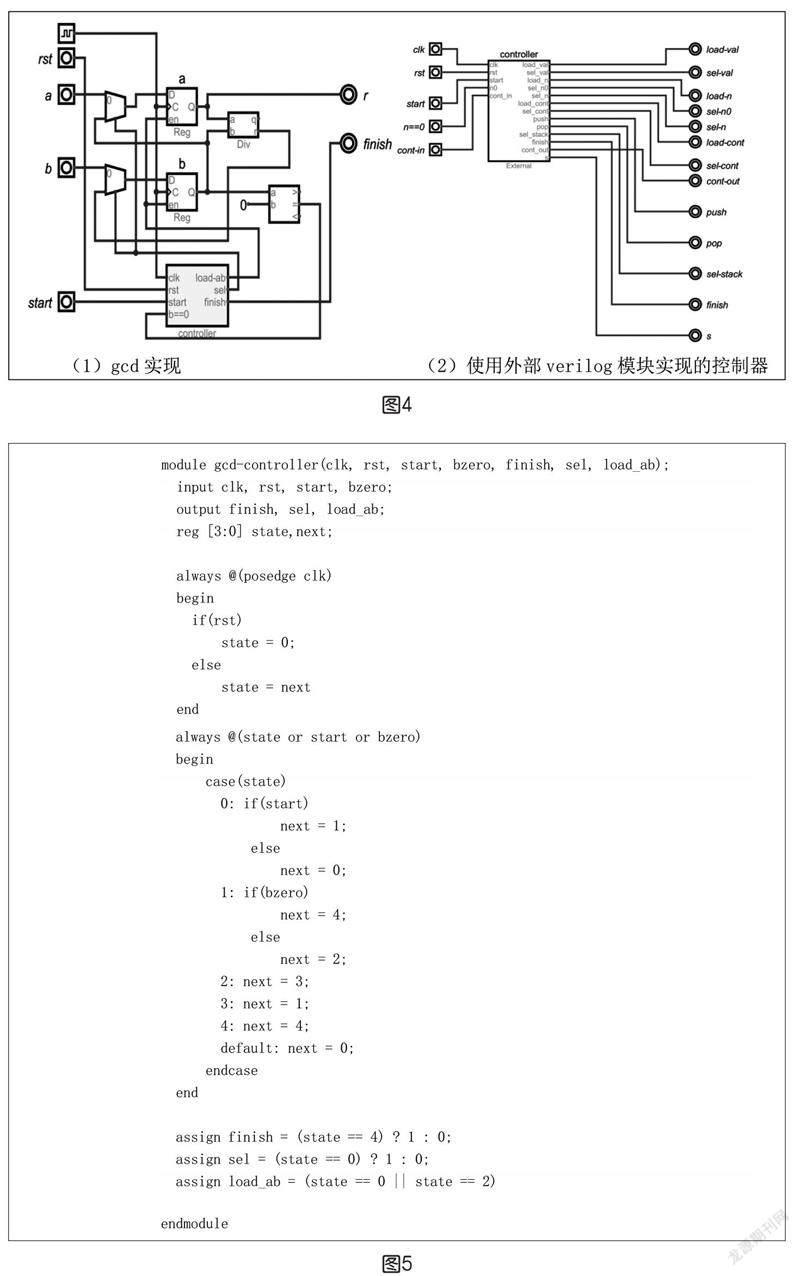
系統使用a和b兩個寄存器、一個取模運算部件、一個比較器，其數據通路如圖4所示。

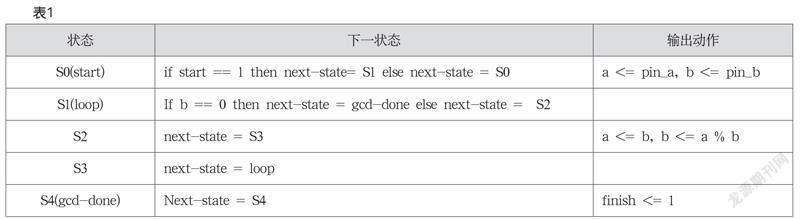
另外，對應的狀態機（增加了讀取輸入）的下一狀態及對應輸出如表1所示。

上述狀態機對應的控制器，可以使用Digital的外部模塊Verilog來實現下一狀態、輸出邏輯，其VerilogHDL代碼如圖5所示。可以看到，采用Verilog描述的狀態機更易于理解和調試。

3.下推自動機設計：階乘（fact）

本案例展示了Digital能夠實現下推自動機這樣的復雜系統。階乘遞歸實現的Python代碼如圖6所示。

與案例二相比，除了最后一條語句，兩者在結構上非常類似。在gcd中，最后一條語句是尾遞歸（Tail-recursion），即gcd（b，a%b）后面沒有其他的計算了。而在fact中則不是，為了計算fact（n），要先計算fact（n-1），然后再計算n*fact（n-1）。而計算fact（n-1），又需要先計算fact（n-2）…，直到fact（0）計算完成，然后再計算fact（1）…fact（n-1）、fact（n）。我們稱n*fact（n-1）是 fact（n-1）的延續（continuation），在軟件中是函數調用后的返回地址，在硬件中則視為一個計算狀態，可將其存儲在堆棧中，當fact（n-1）計算完成后，再從堆棧中恢復continuation，完成fact（n）的計算。

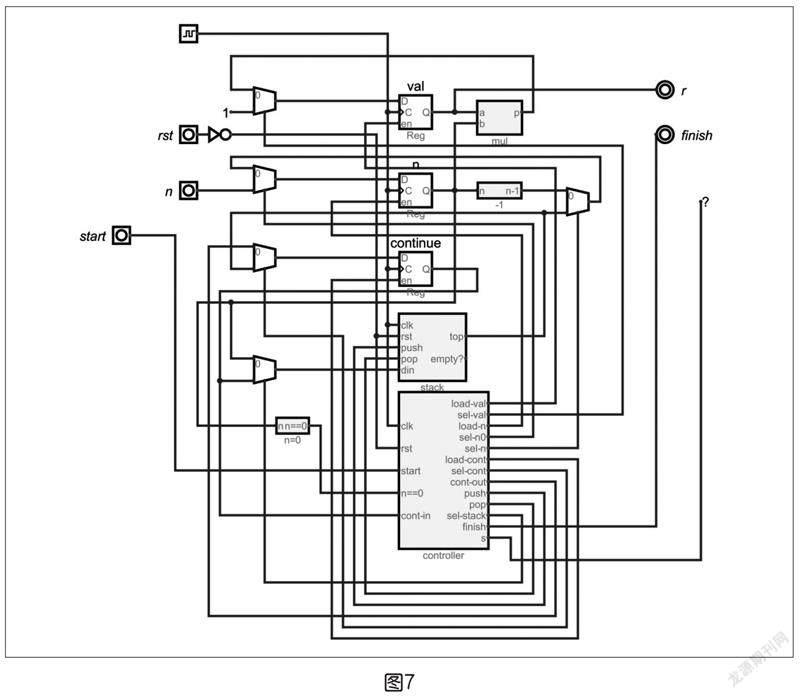
筆者設計了一個包括n、val（保存計算結果）和continue（用于存儲返回狀態/地址）三個寄存器和一個堆棧（用于保存和恢復寄存器n、continue）、乘法器等部件的系統來實現階乘，其數據通路如上頁圖7所示。

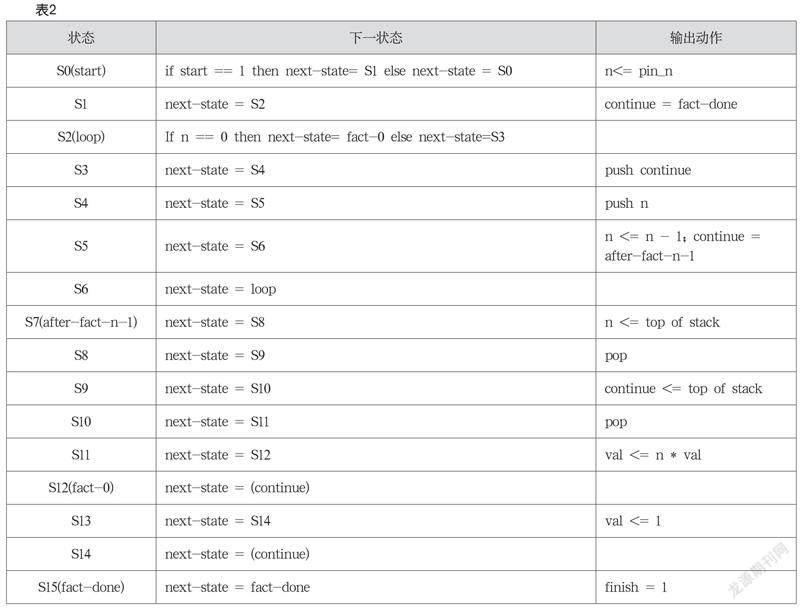
該系統要比gcd系統復雜得多，其對應的控制器狀態轉換如上頁表2所示。

可以看到，為了實現fact的遞歸計算，筆者使用了16個狀態和一個堆棧，這一設計要比案例二復雜很多。同樣，使用Digital的外部Verilog模塊可以大大簡化這個狀態機邏輯的實現，調試也更方便。

4.圖靈機設計：Brainfxxk語言處理器

本案例是一個8指令處理器的Digital實現。Brainfxxk是由Urban Müller在1993年發明的一種只有8條指令的編程語言，該極小化的語言是圖靈完備的，這意味著它可以實現其他任何一種圖靈完備語言（如C語言或Python）完成的計算，甚至可以用它來寫一個Brainfxxk自身的解釋器。

該機器包括一個數組data、一個指向該數組某個單元的指針ptr、程序代碼code、程序計數器pc，以及輸入和輸出裝置。數組data里元素都初始化為零，數據指針初始時指向數組的第一個字節，pc指向第一條指令。其8條指令及其語義分別為：

'>'：將數據指針加一。

'<'：將數據指針減一。

'+'：將數據指針所指的單元加一。

'-'：將數據指針所指的單元減一。

'，'：從輸入流中讀取一個字節，存入數據指針所指單元。

'.'：輸出數據指針所指單元的字節。

'['：如果當前單元是 0，那么跳轉到對應的 ']' 的下一條指令，否則繼續執行。

']'：如果當前單元不是 0，那么跳轉到對應的 '[' 的下一條指令，否則繼續執行。

其對應的C代碼如表3所示。

下面這段代碼：

+++>++<[->+<]>.

等價的C代碼如圖8所示。

該段代碼首先將data第一個單元賦值為3（+++），第二個單元賦值為2（++），然后進入循環（[->+<]），如果第一個單元不為0，則將其減一，把第二個單元加一。在循環結束后，打印第二個單元的值（>.），結果為5。該代碼的作用是將第一個單元值加到第二個單元，并打印。

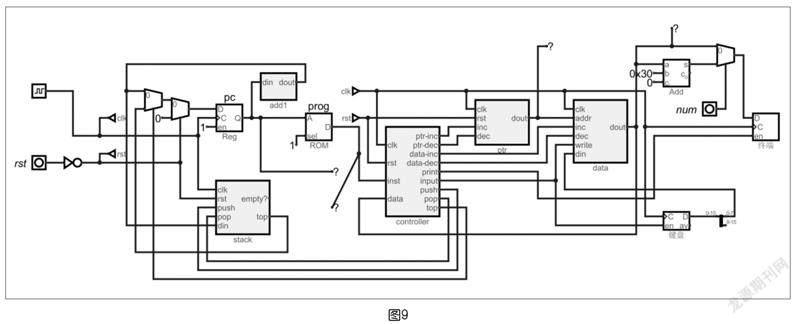
該處理器除了兩條循環指令實現比較復雜之外，其余6條指令的實現是比較簡單的。上頁圖9為該處理器的一個參考實現。

圖9中從左到右，依次為PC及計算下一PC值模塊、程序ROM、控制器controller、數據指針ptr、數據data以及打印、輸入模塊。在圖的左下方為一個堆棧stack，用于記錄循環語句中的起始地址。

控制器的Verilog實現代碼如圖10所示。可以看到，Digital中對Verilog的支持大大簡化了有關模塊的設計，使設計更清晰、更易于理解和排錯。

總結

對于初步具備數字電路基本知識以及C語言程序設計能力的計算類專業學生而言，使用Digital軟件可以很容易了解復雜數字系統的設計和仿真，為進一步完成如流水線、指令動態調度以及轉移指令預測等復雜模塊提供基礎。

參考文獻：

[1]李亞民.計算機原理與設計——Verilog HDL版[M].清華大學出版社，2011.

[2]David Patterson & John Hennessy.計算機組成與設計——軟硬件接口（RISC-V版）[M].北京：機械工業出版社，2020.