多平臺協同偵察定位技術研究

程 翔

(海軍裝備部駐揚州地區軍代室,江蘇 揚州 225101)

0 引 言

無源偵察定位系統是在自身不發射電磁波的情況下,利用輻射源目標發出的輻射信號進行測量,來獲取輻射源的位置,具有電磁靜默、戰場生存能力強、復雜電磁環境適應能力強等特點。在現代戰場環境中,無源偵察定位技術的使用不僅增強了我方的作戰能力,同時也提高了我方平臺的生存能力。現代戰爭的戰法正在由單一平臺和單一傳感器向多平臺及多傳感器的方向發展,無源偵察定位技術在電子戰中有著廣泛的應用并發揮了重要作用,備受各國的重視并在現代戰爭中占據著重要的地位。各國都在不斷提高偵察定位系統在復雜環境下的適應能力,目前使用較多的多平臺定位方法為交叉定位法和時差定位法。

測向交叉法又稱三角定位法,通過高精度的測向設備在2個或2個以上的觀測站對輻射源進行測向,然后根據各觀測站測得的數據以及觀測站之間的距離,經過幾何的三角運算便可確定出輻射源的位置。測向交叉定位系統至少由2個觀測站組成,每個站都配有精密的測向系統,每個站測到的輻射源方位角構成了平面上連接輻射源與觀測站的直線,2條直線的交點就是輻射源所在位置,定位精度主要取決于測角誤差、站址誤差、平臺位置關系等。

時間差測量定位系統則是利用多個位置的接收機接收某個未知位置的輻射源信號來確定該輻射源的位置。多平臺時間差測量定位技術的基本問題是:給定一組平臺及其時間差測量值,如何快速、有效和準確地確定目標的位置[1]。

1 協同定位原理及誤差分析

1.1 測向交叉定位原理及誤差分析

1.1.1 測向交叉定位原理

測向交叉技術又稱三角定位法,在各種平臺上均有實現應用,是一種經典而成熟的無源定位技術。相對而言,在當前愈加密集復雜的電磁環境下測向交叉法也是一種比較穩定可靠的定位技術,因為在復雜電磁信號環境中目標輻射源的方向角是一個緩慢變化的參數。在測向交叉中,對目標到達角的測量是實現目標定位的先決條件,輻射源位置以及測向觀測站的位置如圖1所示。

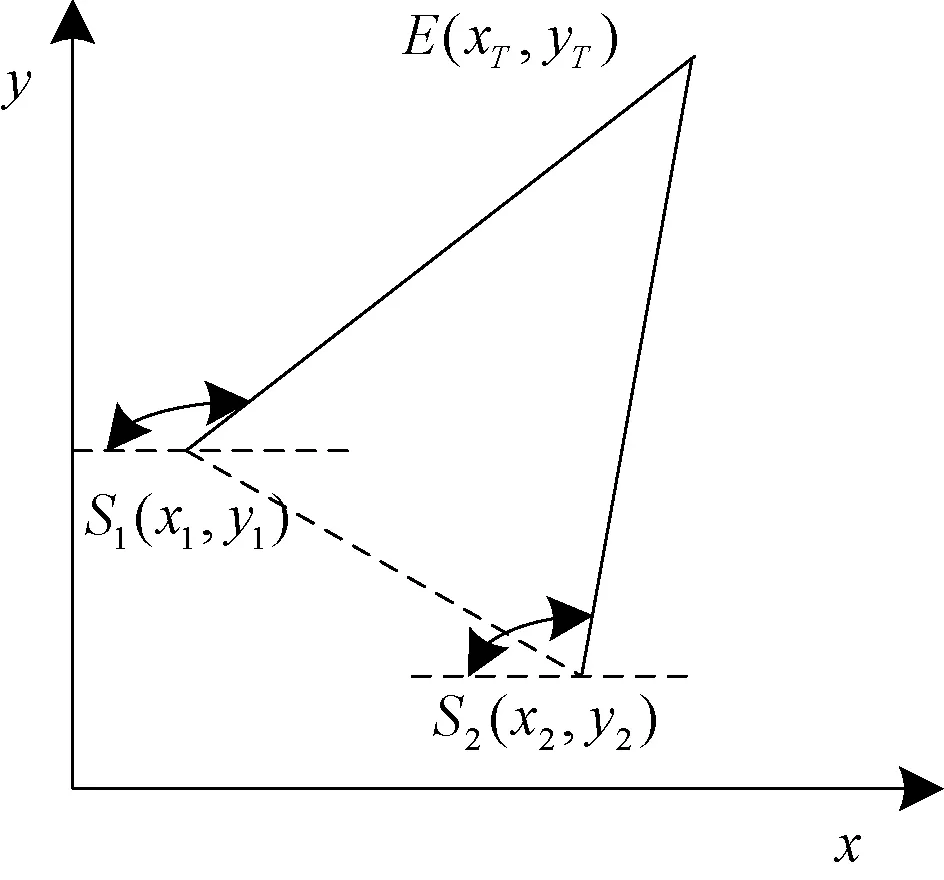
圖1 輻射源與測向觀測站的位置分布

若以X軸的負向為測向基準,由圖1可得到幾何關系為:

(1)

式中:θ1是目標E相對于S1的方位;θ2是目標E相對于S2的方位。

求解方程組可以得到:

(2)

1.1.2 協同定位誤差描述方法

協同定位誤差的大小分布與具體的定位場景、可觀測性、定位方法、參數測量誤差等密切相關,是協同偵察定位系統的重要指標之一。由于目標輻射源的位置不同,即使相同的測角誤差在不同位置所交的區域也不相同。如果測向觀測站的站址固定,定位誤差還是目標位置的函數,為了更好地描述這種關系,工程上定義為定位誤差的幾何稀釋度,或者稱為定位誤差的集合分布[2],如公式(3)和(4)所示,分別表示二維和三維情況:

(3)

(4)

幾何精度因子(GDOP)描述的是定位誤差的分布,它既可以用均方根誤差來表示,也可以用圓概率誤差來表示。為了更直觀地表示目標定位誤差的分布,通常將一個區域的定位誤差分布GDOP描繪成等高線圖的形式,并在其上面標示等高線數值。

由于引起定位誤差的因素是多方面的,根據中心極限定理,定位誤差一般服從正態分布,它們的統計性質往往可以利用分布函數的一、二階矩陣來表示。所以可以利用聯合高斯分布來近似描述定位誤差的分布,對于二維定位的情況,假定定位誤差服從二維正態分布,其概率密度函數為:

(5)

每次使用復雜的概率密度函數來描述定位誤差過于繁瑣,為了進一步簡化定位誤差的描述,可以用一個與概率p相聯系的置信橢圓(稱為概率誤差橢圓)來描述定位誤差。該橢圓的大小和形狀說明了定位誤差的情況,橢圓越大定位誤差越差。在實際應用過程中,描述一個橢圓需要長軸、短軸和方向等參數,使用不便,所以在無源定位的誤差分析中,還是用定位誤差圓來描述定位誤差,如圖2所示,概率誤差橢圓的來源如圖3所示。

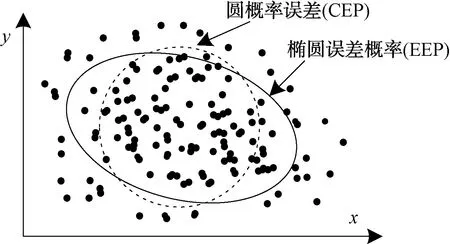
圖2 橢圓概率誤差與圓概率誤差分布圖

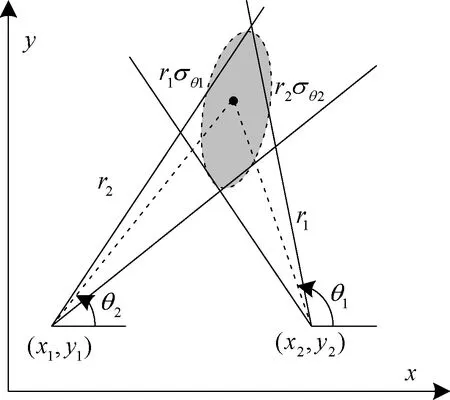
圖3 概率誤差橢圓

圓概率誤差是指以定位估計點的均值為圓心,且定位估計點落入其中的概率為0.5的圓的半徑[3],定義為:

(6)

在誤差不大于10%的情況下,CEP可近似表示為:

(7)

利用定位誤差圓的半徑可說明定位誤差的大小,但不能說明定位誤差的分布情況,而GDOP則可以說明定位誤差的分布情況。

1.1.3 測向交叉定位誤差分析

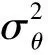
(8)

利用各個單項誤差的標準差合成計算總的標準差具有簡單的優點,同時還不用考慮各個誤差的概率分布,由誤差合成理論可得到:

(9)

取50%圓概率誤差,則CEP可表示為:

(10)

若以兩基站連線所在直線為水平參考軸,則上述公式可以簡化為:

(11)

交叉定位精度與多種因素有關,除了與測向精度有直接關系外,還與目標和2個觀測站構成的三角形形狀有很大關系。

1.2 時差定位原理及誤差分析

1.2.1 時差定位原理

時差定位是根據同一輻射源信號脈沖到達各個觀測站的時間差來對該輻射源進行定位的,由于觀測站無法直接接收到輻射源信號脈沖的發射時間,因此只能通過測得輻射源信號相同脈沖到達不同觀測站的時間差來進行定位。通常需要3個或3個以上的觀測站得出2個或多個時差,來構成多個雙曲面。當只有3個觀測站時,需要加入地球球面方程這個約束條件來構成定位方程組進行求解定位。而對于四站時差定位系統,3個時差方程構成了3個雙曲面,這3個雙曲面相交于一點,該點即為所求輻射源位置[5]。三站時差定位的原理框圖如圖4和圖5所示。輻射源信號到達主站C、輔站B與到達輔站A的時間差為:

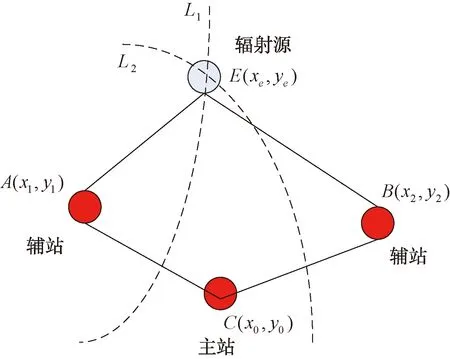
圖4 時差定位觀測站布置框圖

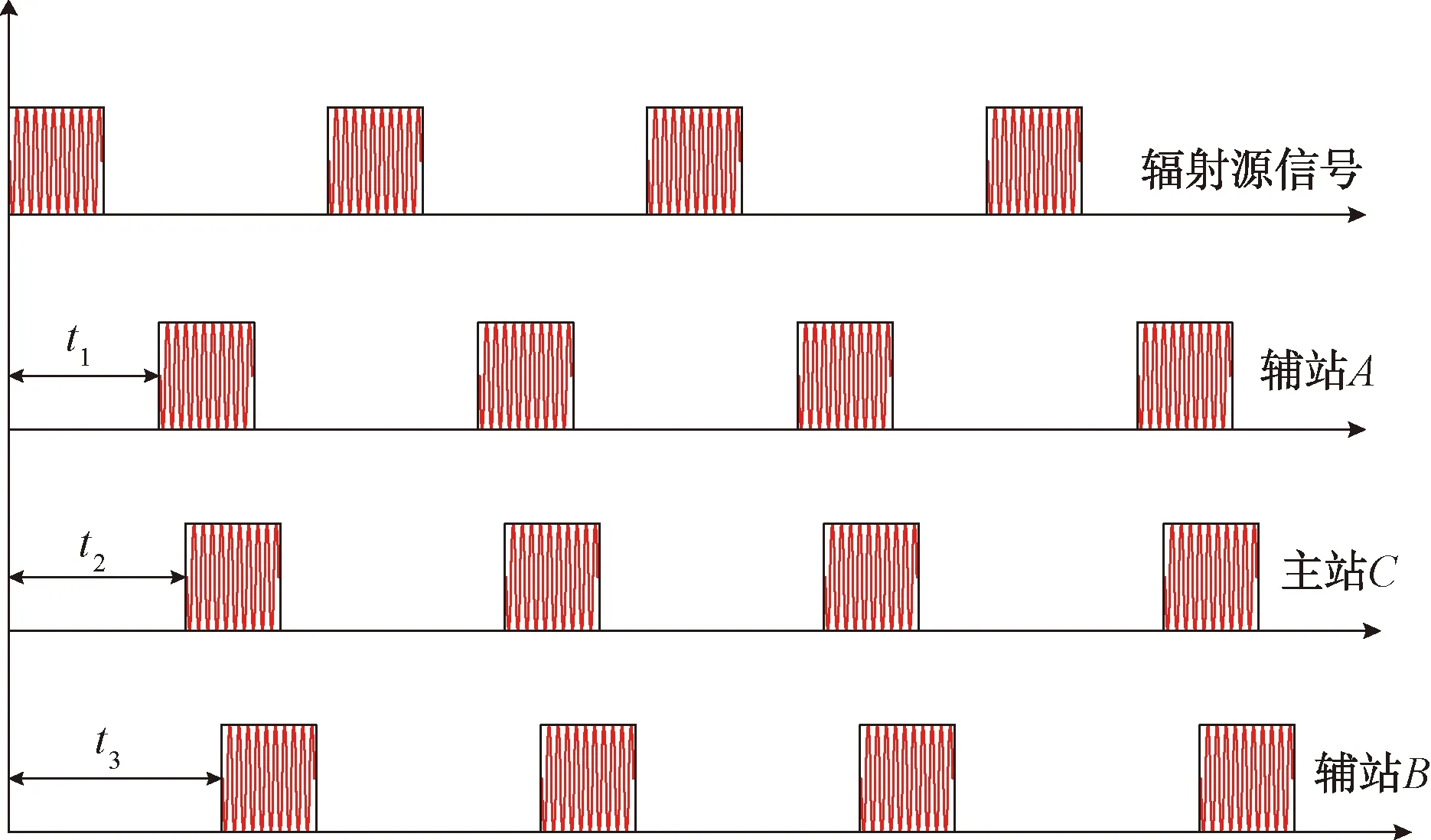
圖5 輻射源信號到達各個觀測站的時序框圖

(12)

平面上的2個觀測站收到同一雷達發射脈沖的時差可以確定1條雙曲線,平面上的3個觀測站時差定位可以產生2條雙曲線,雙曲線的交點即為目標的位置。時差定位的定位精度遠高于測向交叉定位,但是時差定位的定位精度受時差測量精度和觀測站間的集合位置關系限制。

假設空間3部接收機的位置為(xi,yi)T,i=0,1,2,其中i=0表示主接收機,i=1,2表示輔接收機,輻射源的位置為(x,y)T,則定位方程表示為:

(13)

式中:i=0,1,2;ri表示輻射源與第i個接收機的距離;ri0表示輻射源到第i個接收機與其到主接收機之間的距離差;Δti表示目標輻射源到達第i個接收機與到達主接收機的時間差。

1.2.2 時差定位精度分析

時差定位是根據同一輻射源信號脈沖到達各個觀測站的時間差來對該輻射源進行定位的,由于觀測站無法直接接收到輻射源信號脈沖的發射時間,因此,只能通過測得輻射源信號相同脈沖到達不同觀測站的時間差來進行定位。時差定位的定位精度主要與接收機測量的到達時精度相關,在外部同步時鐘穩定的情況下,接收機到達時的測量精度主要與接收機內部時鐘穩定度、噪聲引起的測量誤差、接收檢測處理帶來的測量誤差等相關:

(14)

式中:σ為不考慮同步精度的到達時間(TOA)測量誤差;σ1表示接收機內部時鐘穩定度帶來的TOA測量誤差;σ2表示由噪聲引起的TOA測量誤差;σ3表示由接收機檢測處理帶來的TOA測量誤差。

時鐘穩定度帶來的測量誤差:如果時鐘采用銣鐘,時鐘的穩定度可以達到10-11,每秒鐘的穩定度可以達到10 ps,如果外部同步時鐘進行秒復位,則由內部時鐘帶來的TOA測量誤差為10 ps,基本可以忽略不計。如果時鐘采用晶振,時鐘的穩定度可以達到10-7,每秒鐘的穩定度可以達到100 ns。如果外部同步時鐘進行秒復位,則由內部時鐘帶來的TOA測量誤差為1 μs。所以在進行高精度到達時測量時,需要選用時鐘穩定度更高的銣鐘。

噪聲引起的TOA測量誤差:大多數接收機采用過門限時刻作為TOA的測量值。接收機熱噪聲以及外部環境引入的傳輸噪聲將導致理想脈沖波形受隨機噪聲的影響,引起過門限時刻的測量誤差。在高信噪比條件下,該誤差項可表示為:

(15)

式中:tr為脈沖上升沿時間(脈沖前沿包絡從脈沖幅度的10%增加到90%過程的持續時間),tr的典型值為10～100 ns;σSNR為信噪比。

可以看出,脈沖上升越快,信噪比越高,則測量誤差σ1越小;反之σ1越大。通過仿真分析可知,噪聲引起的TOA的測量誤差通常小于5 ns。

檢測處理帶來的計算誤差:接收機的檢測處理帶來的計算誤差主要與采樣率及快速傅里葉(FFT)算法積累的點數等相關,目前高精度到達時的檢測算法帶來的計算誤差通常小于5 ns。

在分析計算時,TOA的測量誤差體現的就是目標與觀測站的位置誤差,為了分析方便,把式(13)寫成如下形式:

(16)

對上式中的ri0=ri-r0=c(ti-t0)等號兩邊取x,y,xi,yi的微分,得到差定位的誤差公式:

dri0=dri-dr0=

(17)

2 協同定位誤差仿真分析

2.1 交叉協同定位誤差仿真分析

假設兩站偵察設備對目標觀測的測向精度均為1°,則當兩站相距為25 km 時,圓概率相對誤差的分布情況分別如圖6所示。圖中黑線為與兩基站法線夾角±30°的位置。

圖6 兩站相距25 km對目標定位情況

首先考察目標位置與定位基線間的幾何關系對定位精度的影響。設定仿真條件:定位系統的測向誤差為0.5°,兩觀測站位置分別設于S1(-30 km,0),S2(30 km,0)。目標E的位置沿著與x軸方向均勻變化,且與x軸距離分別為50 km、80 km和100 km。雙站交叉定位誤差與x軸方向上的變化曲線如圖7所示。

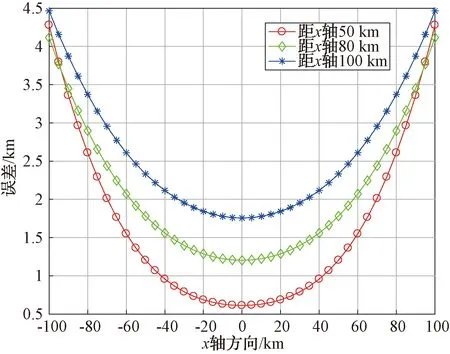
圖7 定位誤差在x軸方向上的變化曲線

接著仿真分析雙站交叉定位精度與偵察距離L、波束夾角的關系。目標位置固定:(0,100 km),兩站偵察距離相同,測向誤差仍為0.5°,定位誤差曲線見圖8。

圖8 定位誤差曲線圖

最后分析定位基線長度和測角精度對定位精度的影響,設定目標位置不變,坐標為(0,100 km),分別改變定位基線長度和測向精度,計算相應的誤差結果如表1所示。

表1 不同基線長度和測向精度下測向交叉定位的定位誤差

分析圖6、圖7、圖8的仿真結果可得到如下結論:

(1)當目標位于定位基線的中垂線方向上時,定位精度最高。

(2)測向精度越高,定位基線長度越大(目標與雙站構成的波束夾角不變時),越有利于提高定位精度。

(3)雙站測向交叉定位誤差大小與波束夾角和偵察距離有關,波束夾角越大(90°范圍內),偵察距離越小,越有利于減小定位誤差,即抵近偵察時定位精度高。

2.2 交叉協同定位誤差仿真分析

本節通過仿真試驗驗證時差定位算法的性能,分別仿真驗證算法的性能和不同位置的GDOP。

首先驗證算法的定位效果,三接收站布陣方式為等邊三角形,主站位于原點處,邊長為40 km,系統測時誤差為100 ns,站址誤差為10 m,分別驗證目標位于點x1(0,100 km)和x2(40 km,100 km)2個點的時差定位效果如圖9、圖10所示。

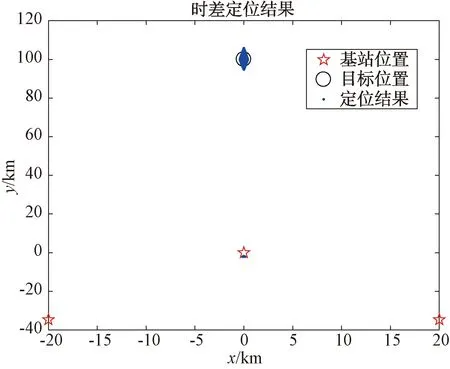
圖9 點x1(0,100 km)定位效果

圖10 點x2(40 km,100 km)定位效果

從上述仿真結果可以看出,當存在測時誤差和站址誤差時,目標定位結果落在距離真實位置一定范圍內,形成一個菱形區域。對比圖9和圖10,不難發現,當目標處于三角形中垂線上時,具有較高的定位精度,而當目標位于兩接收站延長線上時,此時定位精度較差。

接下來驗證時差定位的GDOP,由于布陣方式不同,形成的GDOP分布圖也相差較大。圖11為直線布陣時的GDOP,圖12為三角形布陣的GDOP,圖13為y軸上2種布陣的GDOP對比。

圖11 直線型布陣

圖12 等邊三角形布陣

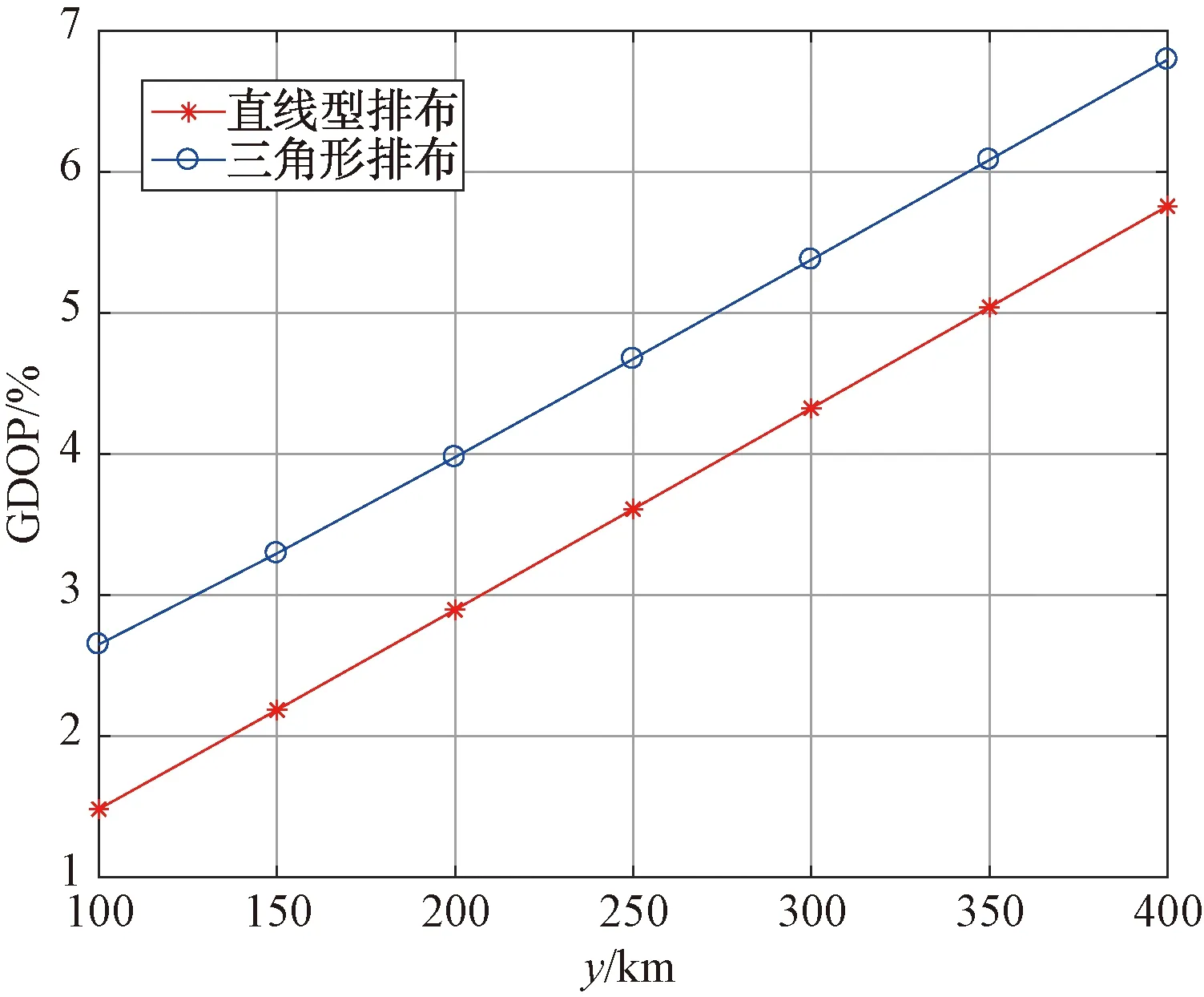
圖13 2種布陣GDOP對比

由圖11、圖12仿真結果可知,當進行三基站時差定位時,定位誤差分布和三接收站中兩兩接收站連線所形成的夾角密切相關,在該夾角區域內,定位精度較高,而在每2個接收站連線延長線所在的區域,無法進行時差定位。從主接收站的角度來看,當其與2個輔接收站連線所形成的夾角越大,則主接收站前方連續定位區域越大,且定位精度較高。因此,在進行編隊作戰時,編隊的布局應該根據戰術需求制定。例如,當偵察目標側重于某地域一側時,那么編隊布局可以選擇近似直線布置方式,以便在偵察區域獲得定位精度較高且作用地域較廣的區域。

最后驗證時間同步精度對時差定位精度的影響,時間同步精度分別取50 ns、100 ns、150 ns和200 ns,站址誤差為10 m,布陣采用三角形布陣方式,對比距離主站不同位置處的GDOP,仿真分析如圖14所示。

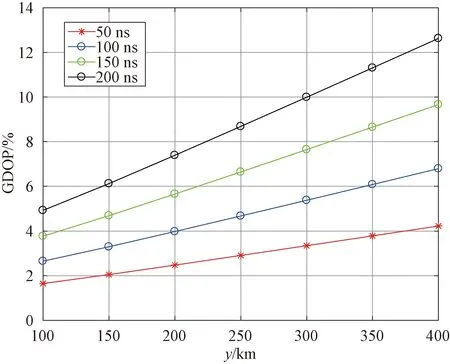
圖14 不同時間同步精度下的GDOP

從圖14不難發現,隨著偵察距離越來越遠,時差定位精度也緩慢下降,距離主站400 km、時間同步精度為50 ns時,時差定位精度小于6%R;當時間同步精度為100 ns時,時差定位精度小于9%R;當時間同步精度為200 ns時,時差定位精度小于15%R,滿足實際工程應用中的定位精度要求。

從以上分析可以看出,在到達時精度有保障的條件下,時差定位精度要比交叉定位精度高。在工程實現上,交叉定位相對簡單,兩站就可以實現交叉定位,實現交叉定位可在輻射源描述字(EDW)級別上實現。而時差定位雖然定位精度較高,但是需要三站同時收到相同的脈沖進行時差比對,在實際使用中存在共視問題,使用局限性較大。所以,在工程中可以結合交叉和時差定位的優缺點,采用交叉和時差聯合定位方法。

3 結束語

多平臺交叉定位和時差定位是無源定位的重要技術手段,在工程中有著廣泛的應用。本文研究了多平臺交叉定位和時差定位的基本原理,通過仿真驗證了交叉定位和時差定位在不同布陣方式、不同測向精度以及不同同步時間精度下的性能。對比分析了交叉定位和時差定位在工程時間中的優缺點,為工程實踐提供了一定的參考。后續需要繼續研究交叉、時差聯合定位方法,時差、頻差聯合定位方法,解決單一定位方法所帶來的局限性。