垂尾裝配尺寸鏈公差分析與優化

張 勇，余志明，陳里根，李根生

（航空工業洪都，江西 南昌，330024）

0 引言

在機械零件生產制造過程中，為保證零件的裝配和互換，設計師在進行零件設計時往往允許零件存在一定的尺寸公差，避免影響到機械產品的質量和裝配精度。在機械裝配或零件加工過程中，離不開尺寸的計算問題，一組首尾相接的相互關聯的尺寸形成一個尺寸鏈。尺寸鏈的合理使用對于保證產品質量、提高經濟效益、降低生產成本具有重要意義[1]。一方面，在零件的加工過程中，根據加工工序，通過尺寸鏈的計算，保證每個工序的加工精度，從而確保零件的精度要求；另一方面，通過尺寸鏈的計算，可以得到間隙即封閉環的大小，判斷其是否滿足產品質量要求，從而以最經濟的方案設計零件加工精度，保證零件互換性，達到預期目的。

某型機垂尾由垂尾安定面和方向舵組成，其中垂尾安定面由前后梁、外蒙皮、肋、長桁等結構組成。垂尾通過垂尾安定面的前后梁單耳接頭與機身框雙耳接頭對接裝配，單耳接頭與雙耳接頭之間通過螺栓固定，如圖1 所示。為保證垂尾的裝配與互換，應避免基于經驗式的尺寸公差分配而造成裝配過程中的零件干涉，本文基于尺寸鏈對垂尾裝配過程中相互關聯的零件尺寸進行公差分析與優化，減少裝配過程中現場不必要的修挫打磨量與加墊調整，提高裝配效率。

圖1 垂尾裝配示意圖

1 尺寸鏈

尺寸鏈是研究機械產品中尺寸之間的相互關系，分析影響裝配精度與技術要求的因素，確定各有關零部件尺寸和位置的合適公差，從而求得保證產品達到設計精度要求的經濟合理的方法[2]。

1.1 尺寸鏈定義與特性

在機械裝配或零件加工過程中，由相互關聯的尺寸連接形成的封閉尺寸組，稱為尺寸鏈。其中，尺寸是包括長度、角度和形位公差的廣義尺寸。

尺寸鏈特性：

1） 封閉性：組成尺寸鏈的各個尺寸按一定順序構成一個封閉系統；

2） 相關性：尺寸鏈中一個尺寸變動將影響其他尺寸的變動。

1.2 尺寸鏈的組成及基本關系式

構成尺寸鏈的各個尺寸稱為環，尺寸鏈的環分為封閉環和組成環。

封閉環：指加工或裝配過程中最后自然形成的尺寸；

組成環：指尺寸鏈中除封閉環以外的其他環，根據其對封閉環的影響不同，又分為增環和減環。

1） 增環：與封閉環同向變動的組成環，同向變動指該組成環尺寸增大（或減小）而其他組成環不變時，封閉環的尺寸也隨之增大（或減小）。

2） 減環：與封閉環反向變動的組成環，反向變動指該組成環尺寸增大（或減小）而其他組成環不變時，封閉環的尺寸也隨之減小（或增大）。

設尺寸鏈中總環數為n，其中有m 個增環，則減環有 n-m-1 個，用 Ai、ESi、EIi、Ti、Δi分別表示增環基本尺寸、上偏差、下偏差、公差、中間偏差；用 A0、ES0、EI0、T0、Δ0分別表示封閉環基本尺寸、上偏差、下偏差和公差、中間偏差，根據完全互換法（又稱極值法），對線性尺寸鏈，封閉環與組成環之間的關系式為：

對非線性尺寸鏈，需考慮傳遞系數ξ，如果是增環，ξ 取正值，減環 ξ 取負值，有：

完全互換法是按尺寸鏈的極限尺寸來計算公差。但是，由生產實踐可知，在成批生產和大量生產中，零件實際尺寸的分布是隨機的，多數情況下，考慮成正態分布或偏態分布。 換句話說，如果加工中工藝調整重心接近公差帶中心時，大多數零件的尺寸分布于公差帶中心附近，靠近極限尺寸的零件數目較少。因此，可利用這一規律，將組成環公差放大，這樣不但使零件易于加工，同時滿足封閉環的技術要求，從而獲得更大的經濟效果。當然，此時封閉環超出技術要求的情況是存在的，但其概率很小，所以這種方法稱為概率法（又稱大數互換法）[3]，其基本關系式為：

式中σ0、σi分別為封閉環和各組成環的標準偏差。 令傳遞系數為 ξ，則：i

式中：e 為相對不對稱系數，k 為相對分布系數，e和k 的取值主要決定于加工工藝過程。大批量生產穩定的工藝過程，其工件尺寸趨近正態分布，取e=0，k=1[3]。

按照統計概率法，某獨立隨機事件重復試驗n次，其統計結果應符合正態分布律，σ 為其正態分布圖的均方差，在±3σ 范圍內正態分布圖的覆蓋率占99.73%，因此，常用統計結果落在正態分布圖的±3σ（即6σ） 范圍內的概率來判斷樣品是否滿足規定要求，這就是6σ 原則[4]。 對組成環和封閉環尺寸偏差服從正態分布，有Ti=6σi，此時封閉環的公差與組成環的公差關系為：

尺寸鏈分析的極值法和概率法求解過程如圖2所示。

圖2 求解過程

2.3 尺寸鏈分析步驟

不管是極值法還是概率法，傳統尺寸鏈分析的基本步驟包括建立尺寸鏈線圖、確定封閉環、判斷增減環、求解未知量[5]。但對總環數較多的復雜尺寸鏈而言，增、減環的判斷耗時易錯，為解決這一問題，文獻[6]提出“矢量五步法”：

1） 分析工況，找出要計算的尺寸（或間隙或過盈）；

2） 將該尺寸的兩端點設定為起點和終點，劃定從起點到終點的方向，即為正方向（+）；反之，即為負方向（-）；

3） 沿起點依次按順序找出每一個首尾相接的關聯尺寸（即組成環），并用箭頭表示其方向，最終回到終點，形成一個封閉的鏈環，此時所有尺寸的方向已唯一確定；

4） 根據所繪制鏈環，箭頭方向與正方向一致的尺寸為正尺寸，反之為負尺寸；

5） 基于零部件實際公差呈正態分布的假設，根據式（12）計算公差值。

2 垂尾裝配

垂尾通過垂尾安定面的前、后梁單耳接頭與機身框雙耳接頭對接裝配，其對接示意圖見圖3。 前、后梁接頭孔內兩側均安裝有相同的帶凸肩的圓環狀襯套，起到保護梁且避免磨損的作用，各接頭之間通過螺栓固定。為保證裝配精度，機身框開有裝配定位孔，其中兩處中心定位孔軸線位于飛機對稱面內，避免裝配偏心。

圖3 對接示意圖

設計時，為避免對接接頭間隙過大，在裝配附注中注有：垂直安定面左側梁接頭與機身框接頭對接處耳片間隙大于0.3mm 時，需要加鋁墊，墊片方向可按需調整。

3 垂尾裝配尺寸鏈公差分析與優化

垂尾裝配分兩部分，先將垂尾各零件裝配成整體，然后將垂尾對接到裝配好的機身框接頭上。裝配對接涉及前后梁接頭、框接頭、襯套等零件尺寸，各零件尺寸如圖4~圖5 所示，單位為mm，根據裝配現場前后梁左側接頭與機身框接頭間間隙進行加墊，保證垂尾正常裝配。

圖4 前梁與框裝配尺寸圖

圖5 后梁與框裝配尺寸圖

3.1 垂尾裝配尺寸鏈分析

3.1.1 垂尾裝配尺寸鏈繪制

根據垂尾裝配尺寸關系，對垂尾裝配進行尺寸鏈分析。 一方面，由于前、后梁與機身框對接形式一樣，為避免垂尾整體裝配受前、后梁對接順序影響，前、后梁接頭，前、后框接頭相互對應尺寸的上下偏差相同；另一方面，由于垂尾是整體與機身框對接，前、后梁對接相互影響，需考慮一方裝配好后另一方與框接頭對接是否會產生干涉從而影響裝配，故需考慮前、后梁裝配尺寸鏈間的相互影響。

由圖6 所示，設計時考慮左側梁接頭加墊，故分析時假設后梁右側單耳接頭、襯套凸肩，機身框右側的雙耳外側接頭相互貼合，前后梁對接尺寸示意如圖7~圖8 所示，根據矢量五步法繪制垂尾裝配尺寸鏈。

圖6 梁與框對接示意圖

圖7 后梁尺寸示意圖

圖8 前梁尺寸示意圖

＞后梁裝配尺寸鏈

1） 后梁兩側接頭與機身框兩側的雙耳接頭對接裝配尺寸鏈：

圖9 尺寸鏈中，X1 為閉環，用于檢驗后梁左側接頭對接時左端是否干涉，或間隙加墊調整，A1、B2 為減環，C2 為增環。

圖9 后梁與機身框對接尺寸鏈-1

2） 梁兩側單耳接頭分別與機身框雙耳接頭對接裝配尺寸鏈：

左側接頭對接尺寸鏈如圖10 所示。

圖10 后梁左側接頭對接尺寸鏈-2

圖10 尺寸鏈中，X2 為閉環，用于確定后梁左側接頭對接時右端是否干涉，此時X1 為過渡環，B1、C2為減環，A1、C1、B2 為增環。

右側接頭對接尺寸鏈如圖11 所示。

圖11 后梁右側接頭對接尺寸鏈-3

圖11 尺寸鏈中，X3 為閉環，用于確定后梁右側接頭對接時左端是否干涉，A1、B1 為減環，C1 為增環。

故有：X3＝C1-A1-B1

＞前后梁相互影響尺寸鏈

后梁裝配對接時會影響前梁對接，由于前、后框都通過中心定位孔安裝，垂尾整體安裝在機身框上，故前后梁對接尺寸鏈可通過中心定位孔軸線（飛機對稱面）傳遞，尺寸鏈如圖12 所示。

圖12 前后梁傳遞尺寸鏈-4

圖12 尺寸鏈中，X4 為閉環，用于檢驗前梁左側接頭對接時左端是否干涉，或間隙加墊調整，X1 為過渡環，A1、B3、E3 為減環，D3、C3 為增環。

＞前梁裝配尺寸鏈

前梁裝配尺寸鏈同后梁裝配尺寸鏈，如圖13 所示。

圖13 前梁裝配尺寸鏈

圖13 尺寸鏈-5 中，X5 為閉環，用于檢驗前梁右側接頭對接時襯套與框接頭是否干涉，X4 為過渡環，A1、E2 為減環，D2 為增環。

尺寸鏈-6 中，X6 為閉環，用于確定前梁左側接頭對接時右端是否干涉，X4 為過渡環，A1、E1 為減環，D1 為增環。

尺寸鏈-7 中，X7 為閉環，用于確定前梁右側接頭對接時左端是否干涉，X5 為過渡環，E1 為減環，D1為增環。

3.1.2 垂尾裝配尺寸鏈求解

根據上述尺寸鏈-1 至-7，采用極值法和概率法對尺寸鏈未知量（閉環）進行求解。

對尺寸鏈-1，極限法求解為：

對于穩定的生產工藝過程，取垂尾零件加工后的尺寸服從正態分布，故概率法求解為：

極限法和概率法進行尺寸鏈分析結果如表1 和表2 所示。

表1 極值法求解結果

表2 概率法求解結果

由表1 和表2，得到極值法和概率法閉環X1-X7尺寸范圍，如表3 所示，其公差及最小極限尺寸對比如圖14 和圖15 所示。

表3 極值法與概率法對比

圖14 公差對比

由表 3、圖 14 和圖 15 可知，

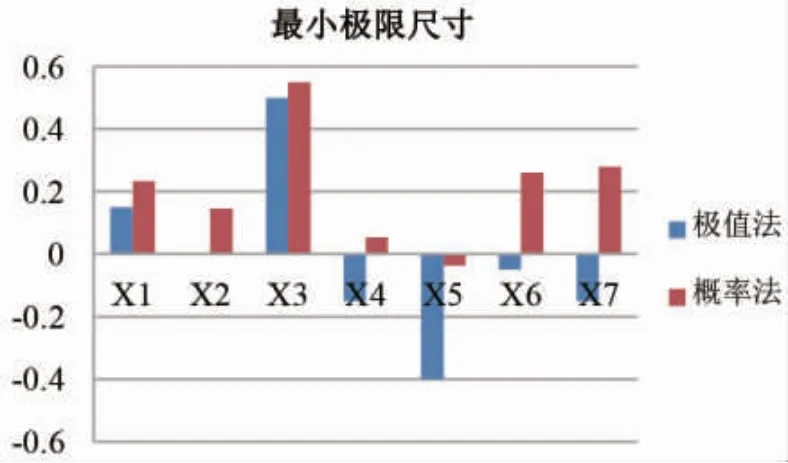
圖15 最小極限尺寸對比

1） 極值法求解的閉環公差大于概率法求解的閉環公差，而閉環是最后形成的尺寸，非實際零件加工尺寸，其公差大。為保證零件完全互換，相應的零件需要較高的加工精度，增加了制造加工成本。

2） 閉環中，無論是極值法還是概率法，都存在最小極限尺寸小于0 的情況，說明后梁裝配好后，前梁與框對接時接頭存在干涉的可能， 需對接頭進行修挫打磨，增加了裝配工作量；其中極值法X4、X5、X6、X7 的最小極限尺寸都小于0， 說明前梁與框對接時左、右接頭都存在干涉的可能，需要對左、右接頭進行修挫打磨，保證完全互換，而概率法中只有X5 的最小極限尺寸小于0，說明前梁右側對接接頭存在干涉的可能，需對右側接頭進行修挫打磨。

3） 相較于極值法，概率法更符合生產實際，垂尾裝配出現不合格性更小，無需多次修挫打磨，有較大的經濟效果。

4） 極值法和概率法求解X1 和X4 的最大極限尺寸均大于0.3，故裝配時，根據裝配要求，需在前梁和后梁左側加鋁墊。

3.2 垂尾裝配尺寸鏈優化

根據尺寸鏈分析可知，垂尾裝配對接時，無論是極值法還是概率法，都存在接頭間相互干涉的可能，為減少裝配過程中現場的修挫打磨，對裝配中尺寸鏈的公差進行優化，調整各尺寸的上下偏差，使封閉環最小極限尺寸不小于0，保證垂尾裝配對接時接頭間存在一定間隙，即：

優化后零件的各尺寸如表4 所示。

表4 優化后尺寸

由表 5 可知，零件尺寸 A1、B1、C1、D1、E1 的公差增大，至少翻倍，即襯套凸緣厚度，前、后梁接頭厚度，機身框雙耳接頭寬度公差放寬，無需高精度，極大提高了零件加工經濟性；其余尺寸公差減小，需提高零件加工精度，保證接頭對接時留有一定間隙，減少后續現場裝配修挫打磨，增加了工作量。

優化后用極值法和概率法求解封閉環尺寸，結果如表5 和表6 所示。

表5 優化后極值法求解結果

表6 優化后概率法求解結果

優化前后閉環最小極限尺寸對比如表7 所示，其柱狀圖如圖16、圖17 所示，由此可知：

圖16 極值法最小極限尺寸對比

圖17 概率法最小極限尺寸對比

表7 優化前后閉環最小極限尺寸對比

1） 經過零件尺寸優化， 極值法和概率法求解的閉環最小極限尺寸均增大且均不小于0，即垂尾現場裝配對接時，不存在接頭間干涉現象，無需進行零件的修挫打磨，可實現垂尾裝配的完全互換。

2） 兩種方法求解X1 的最大極限尺寸均大于0.3，而X4 的最大極限尺寸均小于0.3，故裝配時，只需在后梁左側加鋁墊，前梁無需加墊。

4 結語

本文基于尺寸鏈，考慮垂尾整體裝配時，其前、后梁與機身框對接的相互影響，利用尺寸鏈的空間傳遞，繪制了垂尾裝配對接相關尺寸鏈，并采用極限法和概率法進行尺寸鏈的公差分析。分析表明，垂尾裝配對接時接頭間存在干涉，且均需在梁的左側加鋁墊。 為減少現場裝配時的修挫打磨量，對尺寸鏈公差進行優化，調整各零件尺寸的上下偏差，即零件的加工精度，優化后極值法和概率法求解零件間間隙值均不小于0mm，保證了垂尾正常裝配，裝配效率得到提高，且只需在前梁和后梁一方的左側加鋁墊，無需雙方均進行加墊調整，減少了不必要的重量。