基于分形理論的柱塞泵/馬達配流副潤滑特性研究*

張 嬌 王兆強 韓 博 孫令濤 高 偉

(上海工程技術大學機械與汽車工程學院 上海 201620)

柱塞泵/馬達是流體傳動系統中的重要元件，配流副是其主要摩擦副之一，因其工作環境惡劣從而易發生磨損和失效，因此配流副的潤滑性能是影響柱塞泵/馬達的工作效率及其可靠性的重要因素[1]。由于受到加工精度以及材料成型技術的限制，配流盤的表面并非完全平滑，而是具有一定的表面粗糙度，高壓工況下配流盤與缸體邊緣處油膜厚度降低，配流盤的表面粗糙度可影響到配流副的潤滑性能，故需研究配流盤表面粗糙度對配流副油膜厚度的影響。

國內外學者均對柱塞泵進行了大量的研究，RICHARDSON等[2-3]在軸向柱塞泵試驗臺上安裝近距離探頭來測量配流盤的狀態，同時考慮油液壓力、溫度和彈性變形等因素建立了動態潤滑模型，通過結合理論分析與實驗驗證優化了配流盤的結構，使得最小油膜厚度增加，潤滑溫度降低。CHEN、ZHANG等[4-5]通過多目標遺傳算法對配流盤表面織構進行了優化，并將不同織構條件下的油膜潤滑性能進行了對比，得出在高壓側和低壓側設計不同的織構形狀潤滑效果更佳。以上研究主要針對配流盤表面織構對潤滑和摩擦性能的影響，在配流盤表面形貌方面的研究相對較少，且現有研究較少考慮零件表面原始粗糙度對配流副油膜的影響。

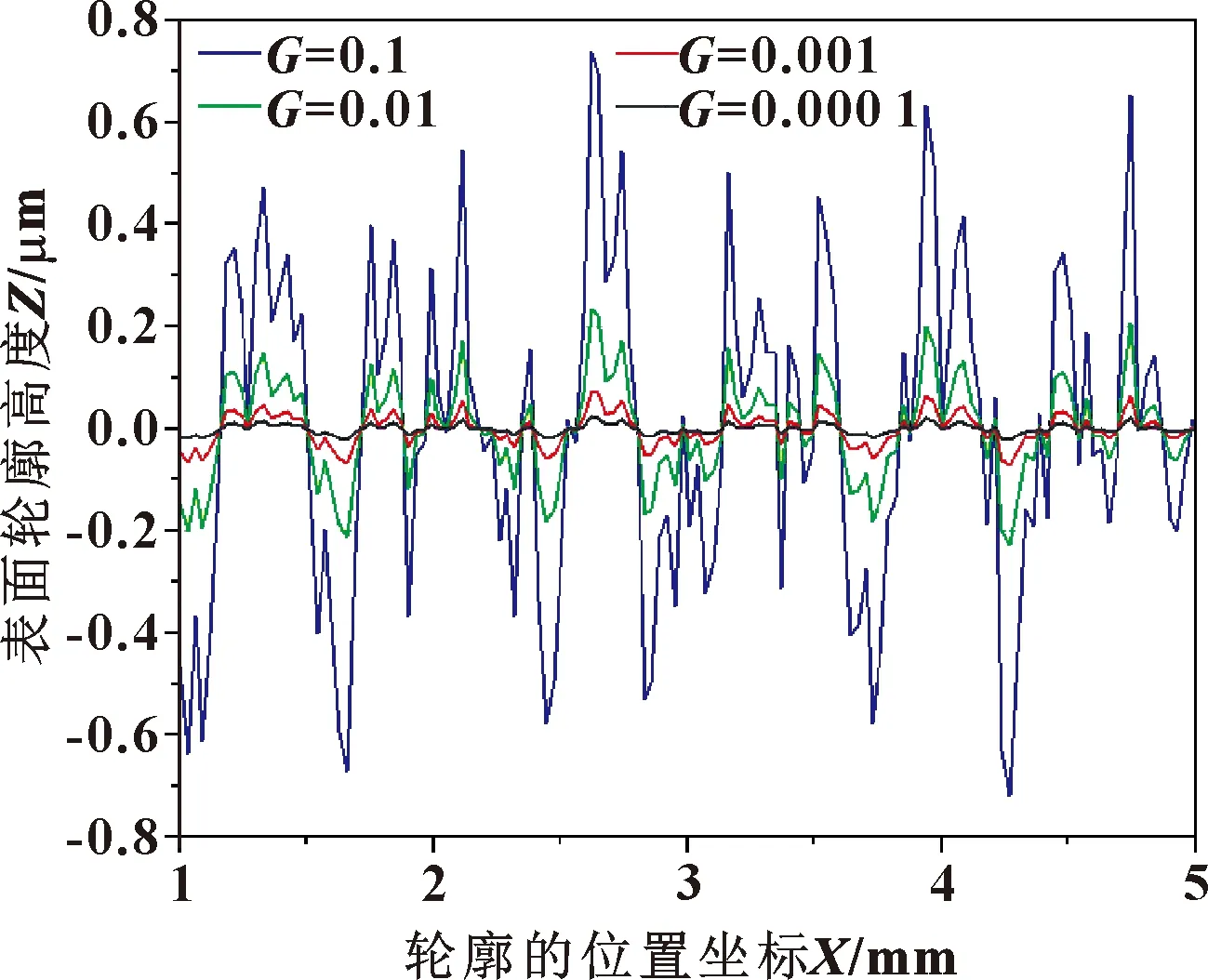
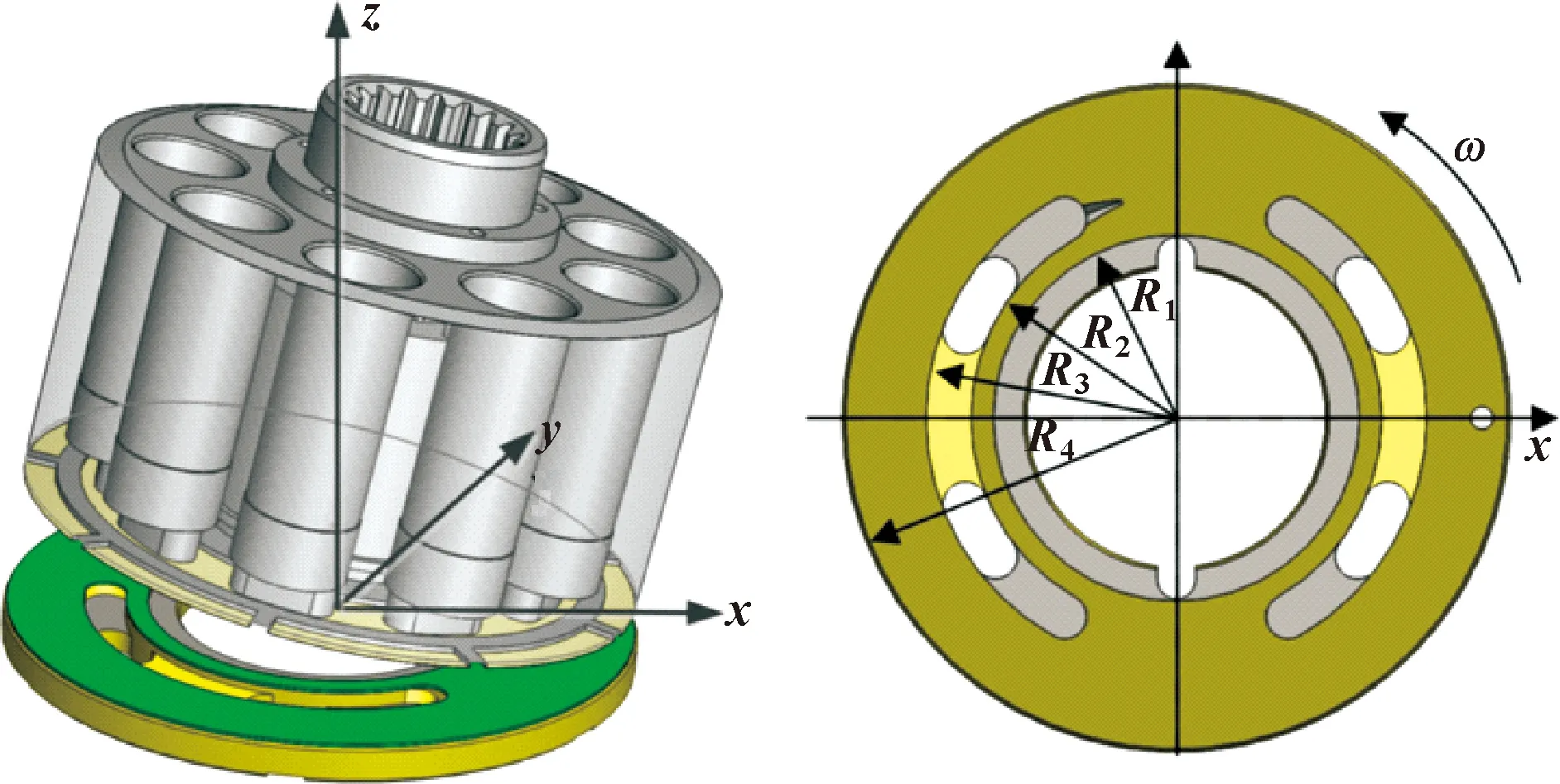
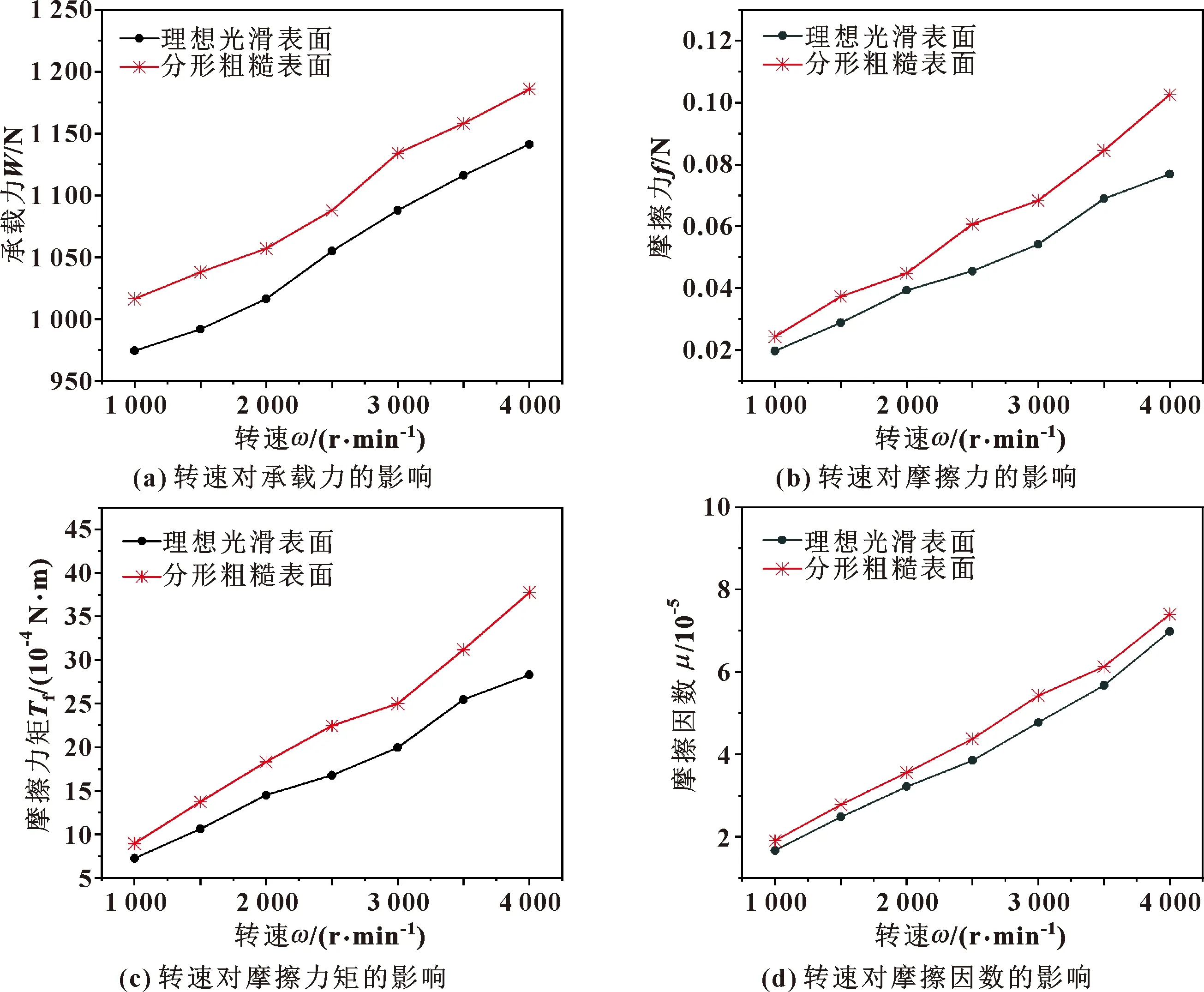
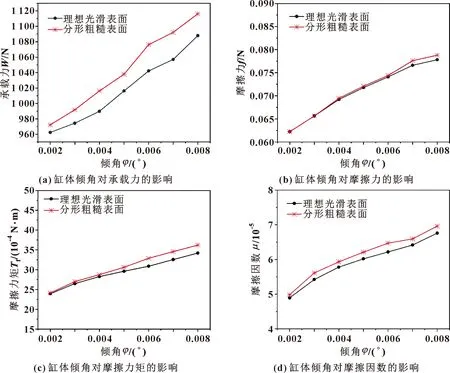
MANDELBROT[6]自1967年提出了分形理論后，分形理論在表面工程研究的許多方面都有著廣泛的應用，比如表面形貌模擬、摩擦、磨損等。SAYLES和THOMAS[7]研究了表面形貌的高度分布特性，由于高度分布具有統計自相似性和自仿射特性，得出工程粗糙表面具有分形特征。1991年，MAJUMDAR和BHUSHAN[8]基于W-M分形函數建立了M-B分形接觸模型，該模型采用具有尺度獨立性的分形參數替代統計學參數來表征粗糙表面。葛世榮[9]分析和討論了磨削和車削的粗糙表面的分形特征，并提出了特征粗糙度的概念來描述表面粗糙水平。CHUNG和LIN[10]基于M-B分形模型，提出了一種用于分析粗糙表面接觸的彈塑性微凸分形模型，該模型相較于之前的預測模型大大減小了誤差。LIOU和LIN[11]在M-B模型的基礎上，考慮到二維模型的局限性，將二維分維(1

基于上述研究，可以得出使用分形理論描述機加工表面輪廓的科學性，因此可以采用分形函數來模擬配流盤粗糙表面，探討配流盤表面原始粗糙度對配流副潤滑特性的影響。本文作者基于分形函數，建立配流副潤滑理論模型，使用有限差分法和松弛迭代法進行理論計算研究，提高了計算精度；同時討論了考慮配流盤表面粗糙度的情況下配流副參數對油膜厚度、油膜壓力分布、承載力、摩擦力和摩擦因數的影響。

1 基于W-M函數的粗糙表面模擬

由于配流盤的表面形貌具有隨機性、自仿射性等特征，可以用分形維數進行表征，使用W-M函數模型來模擬粗糙表面二維形貌和三維形貌，其二維函數表達式為

(1)

式中：z(x)表示x處的二維表面輪廓高度；D為表面輪廓分形維數；G為輪廓的高度尺度系數，取值在[0-1]之間；n為粗糙表面的頻率指數；γ為頻率密度因子，一般令γ=1.5[15]。

從W-M函數表達式中可以看出，分形維數D和尺度系數G是影響該模型的主要參數，為探究D和G與表面輪廓的關系，依據W-M分形函數取適當值進行數值模擬。

首先探討D對表面輪廓的影響，給定除分形維數D之外其他變量的值，改變分形維數D的值，觀察二維輪廓的變化，得到不同分形維數下二維表面輪廓曲線。

為了直觀地看出分形維數D與表面輪廓間的關系，在同一坐標系繪制不同分形維數下的二維輪廓曲線，如圖1所示。可看出隨著分形維數D的增大，粗糙表面輪廓高度逐漸減小，輪廓變得密集，復雜度提升。表明分形維數越大，表面輪廓起伏越小，即粗糙表面越平整，精細程度也越高。

其次分析尺度系數G對表面輪廓的影響，給定除尺度系數G之外其他變量的值，改變G的值，觀察二維輪廓的變化，得出二維表面輪廓曲線如圖2所示。可以看出，隨著尺度系數G的減小，輪廓曲線的形狀相同，表明粗糙表面的復雜程度基本不變，只有表面輪廓幅值減小。

圖2 不同尺度系數下表面輪廓分形模擬曲線

通過探討分形維數D和尺度系數G與粗糙表面輪廓曲線的關系得出，分形維數D主要體現表面輪廓的復雜性，尺度系數G則體現其平整度，同時考慮分形維數和尺度系數2個參數便可確定表面輪廓。

但二維W-M函數對于粗糙表面的模擬具有局限性，為解決二維函數只能反映局部表面輪廓形貌的缺陷，將二維粗糙表面輪廓的W-M函數拓展到三維表面。在已有二維輪廓的W-M模型上，建立了三維W-M函數，其表達式為

ysinBn)+An]

(2)

式中：z(x，y)為點(x，y)處的粗糙峰高度；Cn為尺度參數；Ds為分形維數，Ds=D+1；n為頻率系數；γ為尺度參數，一般取γ=1.5；An和Bn是在[0，2π]范圍內的一系列隨機相位。

對三維W-M函數進行數值模擬，得到不同分形維數和尺度參數下的粗糙表面形貌如圖3所示。

不同分形維數Ds和尺度系數Cn下的三維粗糙表面形貌如圖3所示。分別對比圖3(a)和圖3(c)、圖3(b)和圖3(d)，可以看出，尺度系數不變，分形維數越大，表面輪廓形貌復雜度越高，且變得更加密集，凸峰和凹谷也更多，說明分形維數依舊對粗糙表面復雜性影響較大。分別對比圖3(a)和圖3(b)、圖3(c)和圖3(d)，可以得出分形維數不變，尺度系數越小，粗糙表面復雜度變化基本不變，粗糙表面高度隨尺度系數減小的倍數遞減，說明尺度系數主要影響表面形貌平整性，但并不像二維函數一樣完全不影響形貌的復雜性。

圖3 不同分形維數和尺度參數下的三維粗糙表面形貌

由圖1—3可知，用W-M函數模型來描繪二維、三維粗糙表面的形態特征對表面輪廓曲線的表征效果良好，因此可用作配流盤表面輪廓及形貌的表征。

2 配流副數學模型

柱塞泵結構示意圖如圖4所示，由驅動軸帶動缸體和柱塞旋轉完成吸、排油的工作循環。配流副指的是配流盤和缸體的配流端面組成的摩擦副，配流盤在其中起著高低壓油路分配作用，根據其工作原理可知，配流盤與缸體之間發生滑動摩擦，缸體由于承受來自出油口高壓油帶來的偏載力矩導致缸體傾斜使得與配流盤之間形成楔形油膜從而產生流體動壓效應。為了簡化計算，對配流副數學模型進行如下假設：

圖4 配流副結構示意

(1)忽略體積力和慣性力的作用；

(2)假設潤滑劑為牛頓液體；

(3)由于油膜厚度僅幾十微米，在膜厚方向上壓力變化微小，因此不計膜厚方向的壓力變化。

缸體和配流盤之間的油膜厚度主要受初始油膜厚度h、彈性變形δ(x，y)及表面粗糙度z(x，y)的影響，膜厚方程可表示為

H=h+δx，y+z(x，y)

(3)

其中：

h=h0+r·sinθ·tanφ

(4)

采用雷諾方程求解配流副油膜壓力分布，根據對油膜的假設雷諾方程簡化為

(5)

由上式可知雷諾方程為偏微分方程，方程左邊表示油膜壓力在潤滑表面上隨坐標的變化，方程右邊第一項表示由楔形油膜產生的流體動壓效應，第二項表示油膜在缸體和配流盤2個面的法向力作用下產生的擠壓效應。為方便計算將雷諾方程離散化后采取有限差分法進行計算，可得到較為精確的數值解。

配流副工作過程中流體作用會導致金屬材料產生彈性變形，從而改變其油膜厚度分布，因此需分析配流盤表面彈性變形對配流副潤滑性能的影響。根據彈性變形假說可以得到彈性變形方程：

(6)

由于潤滑劑的黏度受溫度影響，所以配流副油膜溫度也是影響潤滑性能的重要因素，并且溫度過高還可能會引起潤滑劑和表面材料失效。通過數值求解能量方程，可以得到潤滑油膜的溫度分布，二維能量方程為

(7)

依據雷諾方程、能量方程和彈性方程結合W-M分形函數，計算油膜壓力、溫度和彈性變形，計算程序流程如圖5所示。

圖5 計算流程

3 計算結果與分析

為討論表面粗糙度對柱塞泵配流副潤滑特性的影響，根據第1節對W-M分形函數的討論得出的結論可知分形參數影響配流盤的表面形貌，分析不同的配流副工況參數和分形參數下配流副的油膜特性，得到不同表面形貌對配流副潤滑性能的影響。配流副工況參數的初始值如表1所示。

表1 配流副工況參數初始值

3.1 配流副工況參數對摩擦性能的影響

根據柱塞泵工作原理可知柱塞泵缸體轉速及傾角會影響配流副的潤滑特性。為分析配流副工況參數對配流副潤滑特性的影響，選取不同的參數值進行模擬可以得出工況參數對潤滑特性的影響。且當表面輪廓z(x，y)取值為0時即為理想光滑表面，取分形維數為2.5和尺度系數為0.000 1的粗糙表面與理想光滑表面進行性能對比。配流副工況參數的取值如表2所示。

表2 配流副工況參數取值

通過改變柱塞泵轉速分析了缸體轉速對理想光滑表面和粗糙表面配流副承載力和摩擦性能的影響，如圖6所示。從圖6(a)可以看出，隨著轉速的增加導致油膜承載力增加，油膜承載力增加意味著配流副工作過程中缸體與配流盤接觸產生的摩擦磨損會大幅減弱。圖6(b)表示轉速對摩擦力的影響，由于轉速增大使得油膜壓力增大從而摩擦力也隨之增大，相對應地，摩擦力矩和摩擦因數也隨著轉速的增大而增大(見圖6(c)、(d))，使得摩擦效率降低。

圖6 缸體轉速對理想光滑表面和粗糙表面配流副承載力和摩擦性能的影響

控制柱塞泵缸體傾角的變化得到了缸體傾斜角度對配流副承載力和摩擦性能的影響，如圖7所示。從圖7(a)中可以看出，隨著缸體傾角的增大，配流盤與缸體之間的油膜形狀隨之改變，油膜楔形特征更加明顯使得動壓效應增強，從而承載力增大。從圖7(b)—(d)發現缸體傾角增大會使摩擦力增大、摩擦力矩和摩擦因數增加，潤滑性能變差。

從圖6和圖7中可以看出，相對于理想的光滑表面，粗糙表面的承載力略高于理想光滑表面，這是由于粗糙表面存在著許多微小凹坑導致流體動壓效應增強。但同時粗糙表面的摩擦力、摩擦力矩和摩擦因數大于理想光滑表面。

圖7 缸體傾角對理想光滑表面和粗糙表面配流副承載力和摩擦性能的影響

3.2 分形參數對摩擦性能的影響

由于分形維數決定了機加工表面輪廓的復雜度，分形維數一般隨粗糙度的增大而減小，為了討論不同粗糙度下配流副的潤滑特性，選取不同的分形維數Ds和尺度系數Cn進行模擬。

分形維數對配流副承載力和摩擦性能的影響如圖8所示，根據對分形維數的分析可知分形維數越大，零部件表面輪廓復雜度越高，越精細，且粗糙度越小，而尺度參數主要影響表面輪廓高度。

圖8 不同尺度系數下分形維數對承載力和摩擦性能的影響

由圖8(b)—(d)可以看出，隨著分形維數增大，配流盤表面逐漸平整，因此摩擦力、摩擦力矩和摩擦因數也隨之降低；且由于其表面輪廓變得復雜，配流盤表面粗糙峰數量增加使得動壓效應增強，因此承載力增強(見圖8(a))。不同的尺度系數對摩擦性能也有較大影響，尺度系數對表面輪廓高度的影響較大，尺度系數越小表面輪廓高度越低，粗糙表面越平整。從圖8中可以看出，隨著配流盤表面輪廓高度的提升使得油膜厚度減小導致摩擦力增大，但同時由于其粗糙峰高度增加導致動壓效應增強，油膜承載力隨著尺度系數的增加而增大。

4 結論

(1)分形維數D影響表面輪廓的復雜度，分形維數越大表面輪廓起伏越小，精細程度越高。不同尺度系數G下表面輪廓的形狀相同，復雜度基本不變，但尺度系數越小，表面輪廓幅值減小。

(2)由于配流盤表面粗糙峰的存在，與缸體構成了微小的楔形空間，產生了局部壓力峰，因此隨著缸體轉速和缸體傾角的增大，分形粗糙表面的配流盤油膜承載力增大，有利于油膜剛度的提升，改善配流副潤滑環境。但同時摩擦力、摩擦力矩和摩擦因數也隨之增大，又會導致摩擦效率降低，需選擇適當的工況參數。

(3)隨著分形維數的增大，配流盤表面輪廓逐漸平整使得摩擦力、摩擦力矩和摩擦因數都呈下降趨勢，有利于減小磨損，且與此同時配流副的油膜承載力也隨之增加，有利于提升潤滑能力。油膜承載力隨著尺度系數的增大而增大，但其摩擦力、摩擦力矩以及摩擦因數隨之增大，因此可選擇適中的尺度系數以保證在摩擦力較小的情況下同時擁有良好的油膜承載力。