復虹現象的實驗研究

彭子云 漆元臻 李澤宇 梁穎 向紅 韓德專

摘 要 彩虹是一種常見的大氣光學現象，在一定天氣條件下，在彩虹的附近還會出現附加的弧形彩色條紋，這就是復虹。目前關于復虹的實驗研究還十分有限。本文從集體散射與單體散射兩方面對復虹現象進行了實驗研究。通過水霧光散射再現了復虹現象，并測量統計了水滴尺寸及其分布對復虹的影響。然后通過單水滴光散射實驗，研究了不同照明波長、不同水滴尺寸下的復虹現象，從微觀上解釋了復虹的形成機理。我們還利用散射理論計算研究了水滴尺寸及其統計分布對復虹效果的影響，計算結果進一步證實了實驗結論的正確性。

關鍵詞 復虹;水滴尺寸分布;色散;米氏散射

彩虹是一種常見的自然現象，在古代人們就對其做出了各種解釋，而對于彩虹的科學研究則開始于近代。17世紀，笛卡爾提出彩虹是光在水滴內的反射與折射的結果，并運用幾何光學成功計算了虹與霓的角度，但未能解釋色彩的成因。

后來牛頓提出了色散理論，彩虹這一光學現象得到了較好的解釋[1，2]。人們還注意到在一定天氣條件下，在彩虹的附近還會出現附加的弧形彩色條紋，即復虹[1，3]（Supernumerary rainbows）。幾何光學理論無法解釋這一現象。1803 年，托馬斯·楊將復虹解釋為兩角度相同的光束干涉的結果，但該理論與實際現象存在差異[1，3]。1838年，艾里（Airy）提出了“彩虹積分”，更加完備的解釋了復虹現象[1，4，5]。1908年，Gustav Mie提出米氏散射理論，即通過求解麥克斯韋方程組來得到包括均勻球體在內的物體對光的散射的嚴格解。這樣，彩虹以及復虹現象，可以被準確地計算出來[1，6，7]。迄今為止，關于復虹的研究主要集中在理論分析與模擬計算上，例如利用散射理論分析復虹現象及影響因素[8-10]，而實驗方面的研究則非常有限。本論文將從集體散射與單體散射兩方面對復虹現象進行實驗研究，結合理論計算對復虹現象及影響因素給出清晰直觀的解釋。

1 復虹現象簡介

彩虹是光線被水滴散射時發生的一種色散現象[10]。從幾何光學的角度來看，光線進入水滴后會發生多次反射與折射。此過程中，不同位置的入射光線對應不同的入射角，因此出射角度也不同。再由于色散，同一位置入射但波長不同的光線出射角度也不同，從而形成色彩分布。當光線在水滴內反射一次就折射出來時，以40～42度的視角內光最為強烈，形成我們常見的一級虹。如果在光水滴內發生兩次反射再折射出來，則以50～53度的視角內光最為強烈，形成二階彩虹，即通常所說的霓。

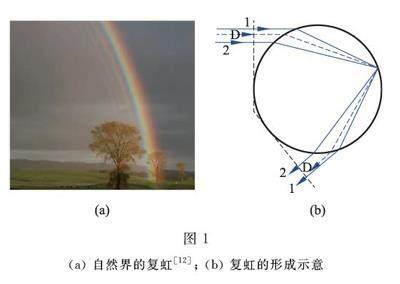
光作為一種電磁波，其波動性會在一定條件下表現出來，例如干涉與衍射現象。相應的，在一定條件下，彩虹中也會出現干涉現象，例如復虹現象。圖1（a）展示了具有復虹結構的彩虹。如圖所示，在彩虹的內側存在多層弧形的彩帶，這些彩帶被稱為復虹。嚴格解釋復虹現象需要用米氏散射理論，但是不夠直觀。用托馬斯·楊的觀點來看，復虹的形成可以解釋為水滴中傳播路徑相近的光線之間的干涉現象。圖1（b）中，光線D代表笛卡爾光線，即偏向角最小的光線，對應觀察到的主虹。光線1與2為鄰近的兩條光線，他們在出射時也保持平行。這兩條光線在遠端（觀察者位置）發生干涉，形成了條紋，白光照射時則形成彩色條紋，即復虹。由于光程差依賴于水滴的尺寸，因此復虹現象與水滴的尺寸及分布都有關系。當水霧中的水滴尺寸差異很大時，各個水滴形成的條紋的角分布不同，在非相干的疊后，條紋對比度會下降。因此只有在合適的條件下才能觀察到復虹現象。一般來說，水滴尺寸越小，形成的干涉條紋越寬，由條紋錯位疊加產生的填補效應就越不明顯。

同時，水滴尺度的分布越集中，條紋填補效應則越弱，也就更容易觀察到復虹。

2 復虹再現與水滴分布測量

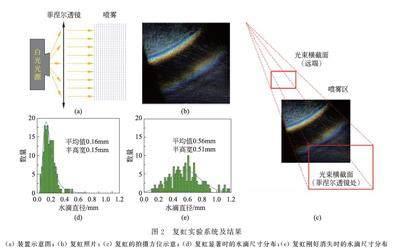
為了研究復虹現象，我們采用了投影儀作為白光光源，菲涅爾透鏡作為準直元件來產生平行光，如圖2（a） 所示，此方案可以獲得橫截面積較大而且平行度較好的光束。在觀察彩虹現象時，利用壓力噴壺在菲涅爾透鏡后噴水霧，在光源一側即可看見虹與霓。通過改變噴壺內壓強以及噴嘴的松緊，可以改變水滴的尺寸及分布。當壓力較大且噴嘴較緊時，在主虹的內側或霓的外側，還能看到一系列明顯的弧形彩帶，即復虹，如圖2（b）所示。當減小噴壺壓力或擰松噴嘴時復虹逐漸消失。圖2（c）以透視畫法示意了復虹的拍攝方位及效果。投影儀發出的光經菲涅爾透鏡準直后形成矩形橫截面的平行光束。照相機位于菲涅爾透鏡的左上方，在此位置上，看到矩形的光束向遠處傳播匯聚到無窮遠處一點。光在噴霧區發生散射，形成以觀察者（照相機）為中心的彩色圓弧。由于立體透視效應，拍攝的虹與霓具有錐狀輪廓。照片中左下和右上的三角區域因沒有光照而呈現出黑色。我們利用分光計測量了虹與霓的角度。實驗中，分光計距離噴霧約1m。測量結果表明，虹處于40～42 度，霓處于50～53 度，與公認值一致。

為 了測量統計水滴的尺度分布，我們利用浸入法測量了復虹現象顯著與復虹剛好消失這兩種情況下對應的水滴尺度。實驗過程如下：首先將盛有植物油的培養皿置于水霧處，開始用擋板遮蓋;然后噴霧，當觀察到彩虹時快速移走擋板，讓培養皿接收水滴，再快速遮蓋住培養皿。最后將培養皿緩慢移至讀數顯微鏡下進行測量。

我們對復虹最顯著和復虹剛好消失這兩種情況下的水滴進行了隨機測量，每組樣本數量為160，并以0.02mm 的間隔進行統計，結果如圖3所示。圖中橫軸表示直徑，縱軸代表水滴數量。

我們嘗試了正態分布和對數正態分布來擬合水滴尺寸的分布。對于復虹顯著的情況，對數正態分布更合適。對于復虹剛好消失的情況，水滴直徑分布更符合正態分布。由于統計方法不同，我們以半高全寬作為彌散程度的統計指標。由圖可知，當復虹現象明顯時，水滴尺寸較小且分布相對集中;而當復虹剛好消失時，對應水滴尺寸較大且分布相對彌散。

3 單水滴光散射實驗

為了研究復虹產生的微觀機理，我們測量了單個水滴對光的散射，考查同一水滴對不同波長的光的散射以及在單色光照明下不同尺寸的水滴的響應。實驗系統如圖3所示。該裝置的核心是分光計，其中平行光管的縫光闌被改裝為小孔光闌。激光（本實驗采用紅、綠、藍激光筆）經過衰減片后照射到透鏡上，再聚焦到平行光管的光闌處，然后經平行光管的準直透鏡后準直為寬截面的平行光出射。單個水滴由注射器產生，水滴的直徑由讀數顯微鏡來測量。激光束照射到水滴后反生散射，用白屏接收，可以看到環形的條紋，這即是單個水滴的光散射現象。圖4展示了局部的散射條紋。轉動望遠鏡對準這些條紋，可以準確測量對應的角度。然后將望遠鏡轉開，將線陣CCD置于剛才望遠鏡的位置，則將這些條紋的光強分布記錄下來。

圖4展示了同一水滴（直徑為2.012mm）在藍光（450nm）、綠光（533nm）與紅光（654nm）照明下的散射光強隨觀察角度的變化。圖中的曲線是CCD探測到的光強信號，其角度信息由分光計測得。這里散射光強做了歸一化處理。曲線的上方是對應的散射條紋的局部照片。這些曲線的左側主峰對應常規觀測到的虹，右側的主峰則對應霓，即二級虹。這里是單色光的散射，不是通常意義上的虹與霓，但是為了方便描述，下面仍以“虹”和“霓”來稱呼。“虹”與“霓”之間有一個暗區，這就是所謂的亞歷山大暗帶。顯然，隨著波長的增大，“虹”與“霓”都向中間移動，亞歷山大暗帶變窄。

而在“虹”的左側與“霓”的右側，還有一系列條紋，這就是單色光的“復虹”。可以看出，波長越小，條紋越密集。

圖5 展示了不同尺寸的水滴在紅光（波長654nm）照明下的散射光強隨觀察角度的變化。

由于散射光強會隨著水滴尺寸的減小而迅速減弱，再加上“霓”的散射光強比“虹”的散射光強更弱，因此對小尺寸單水滴“霓”部分的探測變得困難，我們這里只給出“虹”對應的散射光強。由圖可知，隨著水滴尺寸減小，“虹”的主峰會向角度減小的方向偏移，同時干涉條紋也展寬，這與其他文獻報道的研究結果一致[13]。散射效果對水滴尺寸的依賴進一步體現了光的波動性對彩虹現象的影響。因為按照幾何光學理論，虹的主峰的角位置與水滴尺寸無關。當然，要進一步搞清楚干涉條紋如此分布的原因，需要定量研究入射光經過水滴之后的波前變化。這可以通過干涉實驗來實現，例如讓經水滴出射的光與一束平面波進行干涉，根據干涉圖樣來獲取相關波前的變化。

從上面的實驗可以看出，單個水滴的光散射既依賴于照明波長，也依賴于水滴的尺寸。對波長的依賴，即色散效應，使得水霧的光散射形成彩色的虹與霓。而對水滴尺寸的依賴，則對復虹的觀察效果產生很大影響。不同尺寸的水滴形成的散射條紋的角位置與角寬度都不同，這些條紋的非相干疊加會使得條紋對比度下降。在前面的圖2 所示的實驗中，水滴尺寸小且分布集中時，復虹現象明顯，而水滴尺寸增大且分布彌散時，復虹減弱至消失。這是因為，水滴尺寸越小，條紋寬度越大，越有利與觀察。另一方面，尺度分布越集中，條紋間的錯位越小，對比度越高。同時，由于小水滴的干涉條紋寬，對于尺度彌散導致的條紋錯位容忍度更高。因此，水滴尺度小且分布集中的水霧容易觀察到復虹。

4 米氏散射計算

對于自然界中形成的虹與霓以及復虹現象，波長和水滴尺寸都是連續分布的。我們目前的實驗條件還無法進行相關研究。這里，我們利用米氏散射理論來計算分析波長分布和水滴尺寸分布對復虹現象的影響。米氏散射理論利用多極輻射理論來求解散射問題，是嚴格可靠的計算方法并廣泛應用于散射問題。這里我們采用一個基于米氏散射理論的開源程序[6]來進行相關計算。下面我們考慮尺寸滿足正態分布的水滴的集體散射行為，我們只給出“虹”一側的結果。

首先我們考慮在單色光照明（波長為650nm）下，分布參數對散射結果的影響。在圖6（a）中，水滴尺寸分布的標準差SD 都為10%，但平均尺度不同。可以看出，隨著尺寸的增大，這些散射峰的角度分布更加集中。例如，當水滴平均直徑由0.12mm 增大到0.24mm及0.96mm時，40度附近的主峰與最鄰近次峰的角距離則由3.1度減小到1.9度及0.76度。圖6（b）是平均直徑相同（d =0.12mm）但分布不同的水滴散射情況。由圖可以看出，當水滴分布較集中時，可以看到明顯的復虹;而水滴分布彌散時，復虹的對比度減弱以至于消失。

我們然后計算了復色光照明時的波長疊加效果。圖7（a）展示了尺度正態分布的水霧（平均直徑為0.6 mm、標準差SD=10%）在不同數量的波長照射下的散射強度以及彩虹效果。我們在380～700nm 范圍內等間隔取N 個波長，并基于CIE1931XYZ色彩空間標準[14]合成了顏色。圖中曲線代表散射光強及合成顏色，上方的條形彩圖給出了視覺效果。可以看出當波長數目N =3時，疊加出來的虹的內側有彩色條紋。波長數目增加至10時，虹內側的條紋光強對比度明顯下降，從視覺效果上看，“復虹”就不太明顯了。當波長數量增加到100后，其效果與N=10的情況差異不大。

作為對比，圖7（b）展示了在白光 （380～700nm，100個波長） 照射下，散射效果隨平均直徑的變化。這里水滴尺寸的標準差SD 都為10%。可以看出，水滴尺寸越小，條紋對比度越高，復虹效果越明顯。

這里的計算結果表明：（1）單色光照明時，無論大小水滴都會產生對應于復虹的散射條紋，但尺寸越大，條紋越密集;（2）水滴尺寸分布越彌散，對應于復虹的散射條紋越不明顯;（3）白光照明時，多波長的疊加效果是：尺度越小條紋越明顯，分布越集中條紋越明顯。這與之前的實驗是一致的。

5 結語

本文對復虹現象的形成原因以及影響因素展開了系統的研究。我們在宏觀上實驗觀測了復虹現象并統計了對應的水滴尺寸分布，發現水滴尺寸小且分布集中時復虹現象更明顯，而尺寸較大且分布彌散時復虹現象減弱以至于消失。為了研究復虹現象的形成機理及影響因素，我們實驗測量了單個水滴在單色光照射下的散射行為，獲得了散射光的角度分布及強度信息，得到照明波長、水滴尺寸等對虹與霓及其復虹的影響。同時我們還利用米氏散射理論進行了定量計算，進一步說明了水滴大小，尺寸分布以及多波長疊加對復虹的視覺效果的影響，理論分析與實驗結果一致，合理解釋了復虹的形成機理及影響因素。

參 考 文 獻

[1] HULST H C. Light scattering by small particles[M]. New York： Dover Publications， 1981.

[2] ALEXANDER H. Rainbows in nature： Recent advances in observation and theory[J]. European Journal of Physics，2016，37（6）：1-1.

[3] LAVEN P. Supernumerary arcs of rainbows： Youngs theory of interference[J]. Applied optics， 2017， 56（19）： 104-112.

[4] OUELLETT P E. Supernumerary bows： interference theory with the zero wavefront as a basic element[J]. Journal of the Optical Society of America A-Optics Image Science and Vision， 2019， 36（7）： 1162-1172.

[5] OUELLETTE P E. Supernumerary bows： caustics of a refractive sphere and analysis of the relative overall Gouy phase shift of supernumerary rays[J]. Applied optics，2019，58（3）：712-722.

[6] LAVEN P. Simulation of rainbows， coronas and glories using Mie theory and the Debye series[J]. Journal of Quantitative Spectroscopy and Radiative Transfer， 2004， 89（1-4）：257-269.

[7] 韓凱，許曉軍.基于散射模型的霓虹現象研究[J]. 激光與紅外， 2016，46（3）：334-339.

[8] FRASER A B. Why can the supernumerary bows be seen in a rain shower[J]. Journal of the Optical Society of America，1983， 73（12）： 1626.

[9] SHAN X， XIAHOU C K， CONNOR J N L. Rainbows， supernumerary rainbows and interference effects in the angular scattering of chemical reactions： an investigation using Heisenbergs S matrix programme[J]. Physical Chemistry Chemical Physics， 2018， 20（2）： 819-836.

[10] XIAHOU C K， SHAN X， CONNOR J N L. Rainbows，supernumerary rainbows and interference effects in the angular scattering of chemical reactions： Effect of varying the modulus of the S matrix in the context of Heisenbergs S matrix programme[J]. Physica Scripta，2019，94（6）.

[11] 余虹.彩虹與色散[J].物理與工程， 2017，27（2）：22-25.

[12] Kim. A Perfect Rainbow[DB/OL]. 2018.9.12. https：//writinginnorthnorfolk.com/2018/09/12/a-perfect-rainbow/.

[13] WALKER J D. Multiple rainbows from single drops of water and other liquids[J]. American Journal of Physics，1976， 44（5）： 421-433.

[14] CIE （1932）. Commission internationale de lEclairage proceedings[C]. Cambridge： Cambridge University Press，1931.