Duffing-WS型小世界網絡的混沌行為

常博源 楊京衛 張路

近年來，復雜網絡逐漸成為非線性動力系統研究的一個熱點. 對復雜網絡的混沌行為的產生機制及其對系統參數的依賴進行研究可以為復雜網絡的混沌控制提供理論基礎. 本文研究了一種新的Duffing-WS型小世界網絡的混沌行為. 本文首先利用變分法推導其最大李雅普諾夫指數，并將其作為混沌判據討論了混沌行為對系統參數的依賴. 結果顯示，該網絡具有比單個Duffing方程復雜得多的混沌行為.

復雜網絡； Duffing-WS型小世界網絡； 混沌

O29A2023.021005

收稿日期： 2022-07-11

基金項目： 國家重點研發計劃（2020YFA0714000）

作者簡介： 常博源（1998-）， 男， 山東淄博人， 碩士研究生， 主要研究方向為不確定性處理的數學. E-mail： changboyuan@live.cn

通訊作者： 張路. E-mail： zhanglumail@gmail.com

Chaotic behaviors of a Duffing-WS small world network

CHANG Bo-Yuan， YANG Jing-Wei， ZHANG Lu

（School of Mathematics， Sichuan University， Chengdu 610064， China）

Recently， complex networks become a hot topic of nonlinear dynamical systems. The emergence and parameter dependence of chaotic behaviors is the basis of the chaotic control of a complex network. In this paper， we consider the chaotic behaviors of a new Duffing-WS type small world network. Firstly， we derive an expression for the maximum Lyapunov index by using the variation method. Then we investigate the emergence of chaos by using the Lyapunov index as the criterion. Finally， the dependence of chaotic behaviors on the system parameters is discussed. It is shown that this network possesses more complicated chaotic behaviors than the classic Duffing equation.

Complex network； Duffing-WS type small-world network； Chaos

1 引 言上世紀七八十年代以來，國際上形成了復雜性科學的研究熱潮. 許多復雜性問題都可以歸結為復雜網絡研究［1］. 起初，復雜網絡的研究主要集中于規則網絡或完全隨機網絡［2］， 但這兩種網絡都是理想化模型，現實場景中的系統則往往介于有序和無序之間，即小世界網絡. 小世界網絡通常含有大量的局部連邊，同時也有少量的長程連邊.這些長程連邊有效地降低了網絡中任意兩個節點之間的距離.

1998年，Watts及Strogatz提出了經典的Watts-Strogatz （WS）型小世界網絡模型［3］.該網絡在規則網絡基礎上將每條邊以概率p進行斷邊重連.作者利用該模型模擬了傳染病在人群中的傳播，發現相較于規則網絡，小世界網絡的傳播能力明顯要快得多. 隨后，眾多研究者對各種小世界網絡的動力學特性展開了研究［3-7］. 例如， 2001年，Zhuo研究了小世界網絡的隨機共振現象［4］，發現其隨機共振效應比普通規則網絡要強. 2002年，Hong等研究了小世界網絡的同步性， 發現各振子間的同步性隨重連概率的增大而顯著提高［5］. 2001年，Yang對一個非線性時滯混沌小世界網絡進行了研究，發現網絡的傳播要比規則網絡的速度更快［6］. 2012年，Ning提出了一個基于小世界網絡的離散復雜網絡，研究其分叉和混沌等動力學行為， 發現小世界網絡的混沌現象在適當的參數下會受到控制［7］.

本文進一步研究小世界網絡中的混沌行為. 我們首先提出一個以WS小世界網絡方式連接的Duffing復雜網絡（簡稱Duffing-WS型小世界網絡），利用變分法推導其最大李雅普諾夫指數，并以龐加萊截面分岔圖和李雅普諾夫指數為工具研究該網絡是否能產生混沌. 同時，我們還分析了網絡重連度K、重連概率p和耦合強度ε等對混沌行為的影響. 結果顯示，Duffing-WS型小世界網絡的各個粒子輸出呈現出小尺度周期運動、倍周期分岔、混沌和大尺度周期運動等多種狀態，混沌的參數范圍較單個Duffing方程更為復雜，且各參數對混沌區的影響也與傳統的規則網絡明顯不同.

3.3 耦合強度ε對混沌區的影響

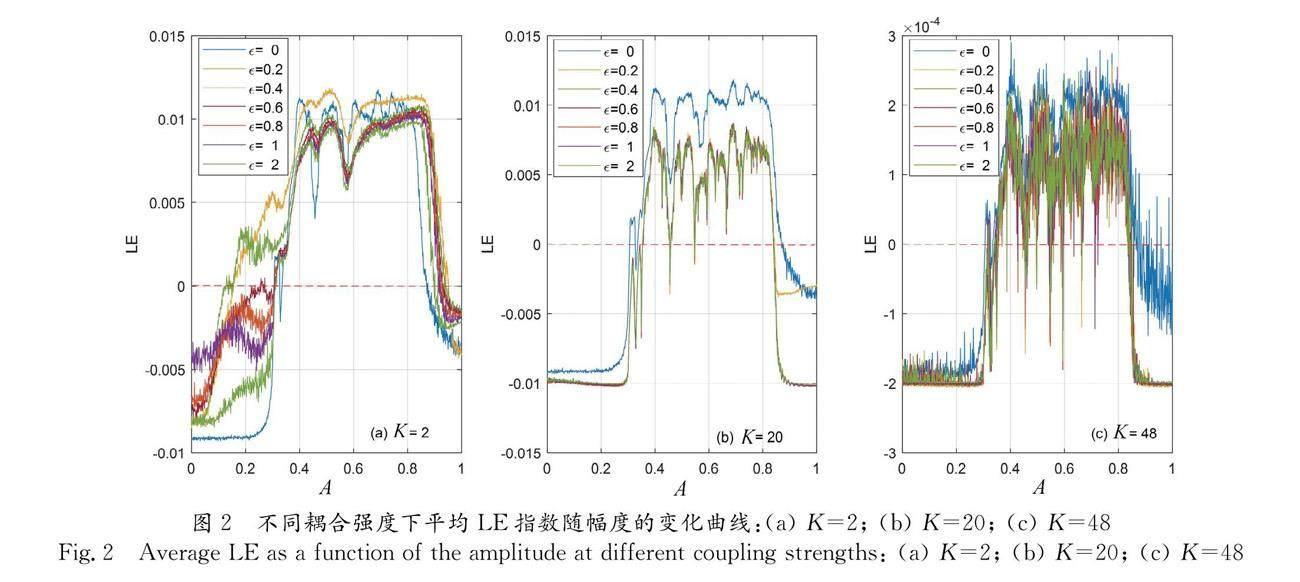
圖2a～2c給出了不同的耦合強度ε下平均最大LE指數隨幅度A的變化曲線，重連概率均為p=0.5. 在圖2a中K=2， 可以見到當耦合強度ε較小時（如ε=0，0.2，0.4），混沌區隨ε的增大而擴大；當耦合強度ε較大（如ε=0.6，0.8，1，2）時，混沌區隨ε的增加逐漸收縮，混沌受到抑制. 這種情況是由于重連度非常小， 節點之間的連接程度不夠，小耦合強度的增強反而增強了系統的混沌運動. 反之，只有耦合強度大到一定程度，更大的耦合強度使得系統協同性增強之后，才能抑制系統的混沌運動.

在圖2b中K=20， 可以看到，當ε=0時，小世界網絡退化成獨立的N個Duffing系統，此時混沌區最大; 當ε>0時，小世界網絡各個節點之間存在耦合作用，網絡的混沌區收縮. 此時由于重連度K值較大，平均LE指數隨幅度A變化的曲線在不同的耦合強度ε下基本一致，即此時小世界網絡的混沌區對耦合強度ε具有魯棒性. 在圖2c中K=48， 同樣可以看到，混沌區隨ε增加的變化同樣不明顯.

綜上，不同于傳統的規則網絡，Duffing-WS型小世界網絡的耦合強度ε對混沌區的影響是非線性的，當重連度K較小時混沌區隨耦合強度的增加先擴大后縮小，K較大時ε的增強對混沌區域影響則不明顯.

3.4 重連度K對混沌的影響

圖3a～3c給出了不同重連度K下平均LE指數隨幅度A變化的曲線，耦合強度均為ε=0.5.在圖3a中，p=0，耦合網絡為規則的最近鄰耦合網絡. 可以看到，當重連度K較小時（K=2，4，6，8，10），隨著重連度K的增加，LE指數大于0的混沌區先擴大后收縮，當K=4時混沌區達到最大；隨后，當重連度K增加到一定程度后（K=20，30，40，48），混沌區隨著K值的增加而有略微地縮小，但總體上差異不大. 這說明，對于規則網絡只有足夠大的重連度才會抑制系統混沌，較小的重連度反而增加系統的混沌運動.

在圖3b中，p=0.5，此時網絡為標準的小世界模型.當 K=2時，LE曲線所對應的混沌區最大，LE指數在各個振幅處的值也最高，可見重連度K較低時更容易產生較大的混沌區.當 K=4，6時，相比K=2的LE曲線，其大于0的區域明顯縮小，即重連度的增加明顯抑制網絡的混沌運動；隨著K值進一步增加，系統LE曲線幾乎沒有變化. 這是因為當重連度足夠高時系統各節點輸出間差異很小，混沌區幾乎一致.

在圖3c中，p=1，此時網絡為完全的隨機網絡. 可以看出，K足夠大時LE曲線的一致性會被打破，重連度對混沌區的控制作用不再呈現明顯規律. 當K=2時，混沌區反而最小，而中間大小的重連度（K=4，6，8，10）混沌區卻較大. 同時，對比完全規則網絡（p = 0）與小世界網絡（p = 0.5），完全隨機網絡的混沌區更大且LE指數更低.

綜上， 類似于完全規則的網絡，Duffing-WS型小世界網絡當重連度K越大時混沌區越小，即K的增大同樣對混沌控制起積極作用，但K增大到一定程度之后這種抑制效果不再明顯. 對于隨機網絡，重連度K對其混沌區的影響也呈現非單調性.

3.5 重連概率p對混沌的影響

圖4a～4c給出了不同的重連概率p下平均LE指數隨幅度A變化的曲線，耦合強度均為ε=0.5. 在圖4a中，K=2，在圖4b中K=20， 可以看到，不同重連概率p對混沌區的影響不明顯，差異主要體現在LE指數的高低上，重連概率p越大，LE指數值越小. 在圖4a中，K=48， 這種情形下混沌區明顯后移. 總的來說，此時小世界網絡的混沌區對重連概率p具有魯棒性.

4 結 論

本文研究了一種新的Duffing-WS型小世界網絡模型的混沌行為，通過變分法計算其最大李雅普諾夫指數，進而分析了不同參數對其混沌區的影響. 我們發現，Duffing-WS型小世界網絡具有比單個Duffing-方程更為復雜的混沌行為，且系統重連概率、重連度以及耦合強度對系統混沌區域的影響也有別于傳統的規則網絡.

（i） 網絡耦合強度ε對混沌區的影響并不是單調的. 當網絡重連度K較小時，耦合強度的增強反而會促進系統的混沌. 只有在重連度K增大到一定程度之后，較強的耦合強度才會對混沌起到控制作用，但是當重連度K足夠大后系統再次產生混沌.

（ii） 網絡重連度K在不同重連概率p下對混沌有明顯的影響. 對于規則網絡（p = 0）和小世界網絡（0< p <1），足夠大的重連度會抑制系統的混沌，較小的重連度則促進系統的混沌運動. 與前面兩種網絡相比，完全隨機網絡（p = 1）的混沌區則更大，重連度K對其混沌區的影響也呈現非單調性，隨著重連度K的增加，其混沌區先增加后減小.

（iii） 網絡重連概率p對復雜網絡混沌區的影響不明顯.

參考文獻：

［1］ Newman M E J. Networks ［M］. New York： Oxford University Press， 2018.

［2］ Buchanan M，Aldanagonzales M. Small worlds and the groundbreaking theory of networks ［M］. New York： Norton， W. W. & Company， Inc， 2003.

［3］ Watts D J，Strogatz S H. Collective dynamics of ‘small-world networks ［J］. Nature，1998，393：440.

［4］ Gao Z， Hu B， Hu G. Stochastic resonance of small-world networks ［J］. Phys Rev E， 2001， 65： 016209.

［5］ Hong H， Choi M Y， Kim B J. Synchronization on small-world networks ［J］. Phys Rev E，2002， 65： 026139.

［6］ Yang X S. Chaos in small-world networks ［J］. Phys Rev E， 2001， 63： 046206.

［7］ Ning L， Sun H Y， Zhang Q L. Bifurcations and chaos control in discrete small-world networks ［J］. Chinese Phys B， 2012， 21： 010503.

［8］ Akhmet M U，Fen M O. Chaotic period-doubling and OGY control for the forced Duffing equation ［J］. Commun Nonlinear Sci， 2012， 17： 1929.

［9］ Steeb W H.非線性系統手冊［M］. 徐玉秀， 譯. 北京： 電子工業出版社， 2013.