從“苦學”到“樂學”,悟思維之靈動
彭曉梅
著名數學家華羅庚也說過:“就數學本身來說,也是千姿百態,壯麗多彩,引人入勝的。”數學為什么“好玩”?數學憑什么“引人入勝”?因為數學美啊!
數學美在對稱,美在簡潔,美在嚴謹,美在秩序,美在規律,更美在思維之靈動,對于同一個題目能從不同的角度用多種解題方法和思路解答。今天我結合一個實例通過活躍的思維來體會數學之美。
在學習了角的基本知識之后,學生們對鐘表的時針和分針所形成的夾角的度數問題產生了極大的興趣,但是在求解的過程中卻遇到了一些困難,根據學生們思考角度的不同,我把時針與分針的夾角問題總結出多種解題方法。
一、基本知識鋪墊
普通鐘表相當于圓,其時針或分針走一圈均相當于走過360°角,360度角被分成12格,一格對應的角度為30°,這一格分針需要用五分鐘走過,時針需要用一小時即60分鐘走過,時針的一小時或分針的 5 分鐘因而時針每走過1分鐘對應的角度為0.5°,分針每走過1分鐘對應的角度應為6°。
二、計算舉例(此類題目需要注意,我們要求的夾角問題默指小于180°)
例:鐘表上時間為 3:40 時,計算時針與分針夾角的度數
(一)解法一:利用角的和差關系
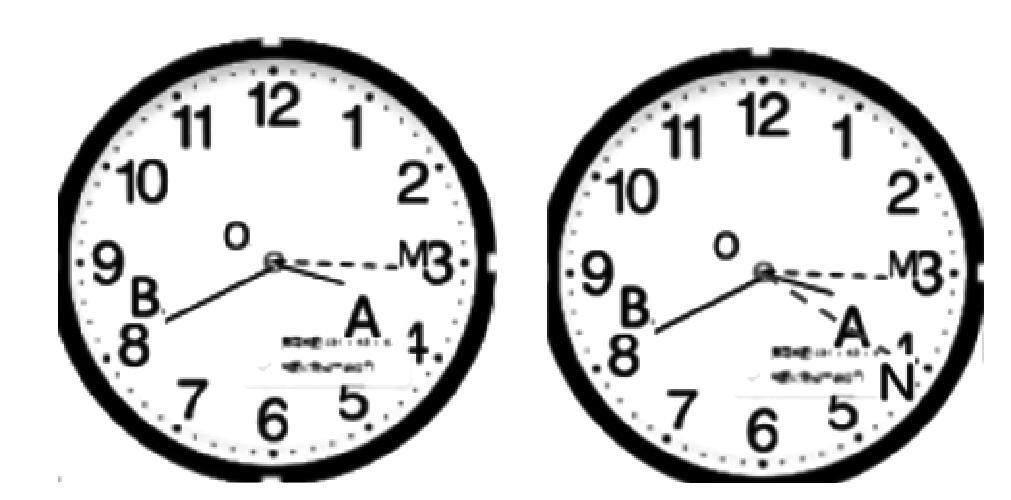
此題中我們要求的角度為圖中的∠AOB
∠AOB=∠MOB-∠MOA
∠MOB=30°×5=150°
∠MOA=0.5°×40=20°
所以∠AOB=∠MOB-∠MOA=150°-20°=130°
或者∠AOB=∠NOB+∠NOA
∠NOB=30°×4=120°
∠NOA=30°-∠MOA=30°-20°=10°
所以∠AOB=∠NOB+∠NOA=120°+10°=130°
(二)解法二:可以把這個問題看成行程問題,求路程差(默認時針和分針的原始位置都是從指向12也就是0時0分開始)
解析 :依據常識,我們應該以時針、分針均在12點時為起始點進行計算由于分針在時針前面,我們可以先算出分針走過的角度,再減去時針走過的角度,即可求出時針與分針夾角的度數。
1.先看分針:從原始位置0時0分到3時40分,共轉過40分鐘,所以分針走過的路程為40×6°=240°。
2.再看時針:從原始位置0時0分到3時40分,共轉過3小時40分鐘,即220分鐘,所以時針走過的路程為220×0.5°=110°。
3.此時分針走過的路程比時針多,所以夾角為240°-110°=130°。
注:路程差即為路程的差的絕對值(在某些時刻時針走過的路程比分針走過的路程多)。
(三)解法三:可以把此問題看成追及問題
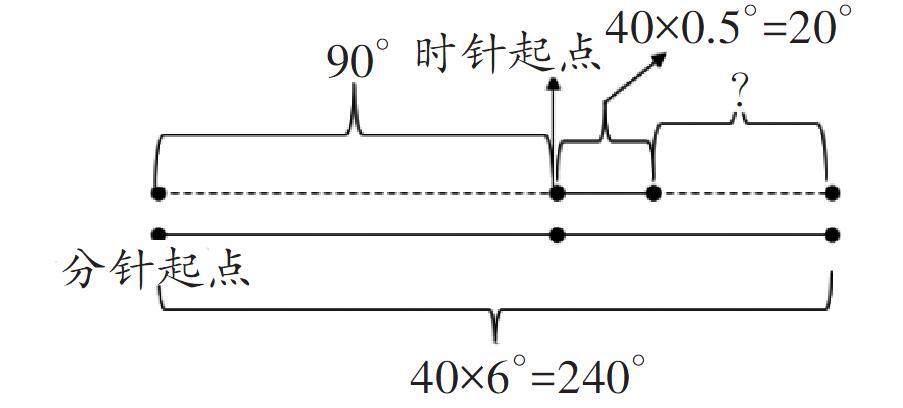
解析:我們可以把時針和分針回歸到整點,3:40即回到3:00,從3:00到3:40,分針和時針都在跑,最終分針超過了時針。我們可以用線段圖來表示:
由線段圖不難看出,我們要求的角度=240°-90°-20°=130°。
三、總結
以上三種方法各有自身的優點,結合教學經驗,可以把它們的優缺點總結如下。
解法一把所求角度轉化成線段和差問題非常的直觀,但是不同的時刻圖形不一樣,需要每個題目分別對應分析。
解法二可以總結出一個求夾角的公式,例如x時y分所成的夾角即為:
|0.5(60x+y)-6x|=|30x-5.5y|,這個公式可以不用看圖直接套用求角度。
解法三把鐘表問題看成一個行程問題,也就是類似于我們之前學過的操場上跑步的問題,這個可以與一元一次方程結合起來,讓學生的思維更開闊,更靈活,這種方法更適合于求時間差的問題,例如“某人下午6點到7點外出購物,出發和回來時發現表上的時針和分針的夾角都是110°,此人外出購物用了多少分鐘”,在追及問題中我們都知道時間差=路程差÷速度差,所以此題結果為220÷5.5=40分鐘。
上述問題只是眾多數學課堂中的一小節,當上述解題思路在數學課堂中得以展現的時刻,可以想象到學生們在課堂上思維碰撞的激烈和收獲的喜悅,當學生的思維活躍起來,就像足球場上奔跑的運動員,他們感受不到揮汗如雨的勞累,只能感受到收獲后心中滿滿的美。
在數學教學中,要充分挖掘數學美的因素,引導學生逐步體驗到數學美,從直覺到知覺,從知覺到感悟,使他們走入“樂學”的天地。

