超大地下空間施工期抗浮控制研究

何晉飛

摘要：在我國城市化快速發展的背景下，特大型地下空間被廣泛應用于城市建設，既有建筑的抗浮力受到新的挑戰。目前，國內外對工程結構的抗浮設計多集中在工程竣工后的服役期，而對容易發生事故的建設期缺乏深入的研究。本文主要研究一種基于施工期可靠度的建筑施工現場地下水位安全預警方法及系統。

關鍵詞：地下空間；地下水位；抗浮控制

一、超大地下空間施工期抗浮控制系統

將可靠性分析用于抗浮問題中，基于可靠度指標評價結構的抗浮能力。在此基礎上，本研究提出一種新的抗浮力分析方法，該方法可用于對抗浮力分析和預報。與此同時，本研究還提出了一套以可靠性指數為基礎的抗浮預報與預警體系。

應用此系統進行施工期抗浮控制，應充分考慮建筑構件尺寸、材料屬性及水位分布的隨機性對抗浮的影響，提前預測結構在施工期發生抗浮失效的概率，以此有效避免事故的發生。本研究提出的方法適用于以抗浮樁或抗浮錨桿為抗浮措施的地下室結構。

二、工藝原理、流程及操作要點

（一）工藝原理

將可靠性分析、水位預測結合應用，組成可以提前預測事故發生概率的抗浮預測預警系統。施工期是大型地下結構易于發生抗浮事故的高峰期。在此系統中，應將施工期細化為幾個階段，基于可靠度指標對各個階段的抗浮能力進行評價，得到事故發生的概率。通過對工程現場的氣象條件、地形地貌和水文地質條件的分析，建立工程現場的地下水位預報模式。在此基礎上，利用預報水位作為超前預報可靠性指數，從而實現對地下工程的防浮預報和預警，有效規避

防浮事故。

（二）工藝流程

建立場地地下水數值模型→水位預測→水位數據統計整理→水位分布→建立結構有限元模型→有限元模型可靠性分析→施工期預警可靠度指標→施工期事故發生概率→提供施工期抗浮專項方案。

（三）操作要點

1.水位預測

使用數值模擬的技術來模擬地下水的流動狀態，進而實現水位預測。首先，在 ARCGIS平臺上，利用 GIS技術獲取地理信息數據，并使用 FEFLOW對現場建模，通過對所獲取的各種數據整理，包括水文地質條件、氣象氣候條件、地形地貌等，并結合現場監測數據，最終實現現場水位的預測。

（1）針對該地區的實際情況，提出一種基于該地區的水文地質概念模式，并進行數值模擬。

（2）根據水文地質資料，確定水文地質和其他介質的相關屬性，確定源、匯相等參數，建立區域地下水模型。

（3）通過試驗結果與仿真結果的比較，檢驗模型的精度，進而獲得更加符合真實情況的水力學參數，從而改進 FEFLOW地下水數學模式，預估水力條件。

水位預測流程如圖1所示。

2.可靠性分析

在工程可靠度分析的基礎上，基于對建筑結構的工程需求以及其對應的極限狀態，構建出表達其極限狀態的函數。在研究抗浮時，主要從抗力與效應兩個角度考慮，以此可以將極限狀態用數學公式表示為式（1）所示。

（1）

式中，S—荷載效應，表現為水浮力上浮效應；

R—結構的抗力，表現為結構抗浮效應。

在防浮設計中，抗力主要表現為結構的自重，主要受構件尺寸、材料屬性及施工進度等的影響，效應主要為水的浮力，因此，可以將式（1）表示為式（2）。

（2）

令式（2）等于0，也就是 Z=R–S=0，可以得到結構的極限狀態方程，用來表達極限狀態面（或失效面），并將功能函數定義域Ω劃分成為可靠域

Ωr與不可靠域Ωf。當 Z<0時，結構處于故障狀態；當 Z=0時，為結構的極限承載力；當 Z>0時，該構件仍為可供正常工作的構件。

3.高階矩法

在可靠性分析中，矩法中的低階矩法如一次二階矩法等應用較多，其具有計算簡單高效的優點，但無法保證選取的隨機變量的分布概型是否正確。本文提出使用高階矩法進行可靠性分析，可有效彌補低階矩法的不足。首先利用改進的雙變量降維法求得功能函數的統計矩再利用Pearson系統擬合概率密度函數求得失效概率（表1）。

首先，功能函數的前四階矩可以用積分表示為：

（3）

（4）

（5）

（6）

式中，μz、σz、γz和Kz分別代表功能函數的輸出值的平均值、標準差、偏態系數和峰態系數；表示功能函數；表示Z的概率密度函數；表示x的聯合概率密度函數。將式（3）～式（6）統一寫成如下積分：

（7）

代表函數的頭 i階初始矩陣，最初的隨機輸入變量被歸一化，也就是被轉化為標準的正態分布的空間：

（8）

式中，代表同一分布變量間的Rosenblatt轉換、Nataf轉換或線性轉換的逆轉換；Θ代表一個包括 n個相互不相關，在一個標準正態空間中的隨機變量；H是一個自變量Θ的函數且它的函數值可以精確計算出來。也就是說，既可以將x代入的函數方程中獲得 H，又可以由x變換獲得標準變量Θ。通過變換，就可以將式（7）變換為：

（9）

采用二元降維能有效地實現該高階矩陣的有效求解，但當存在大量的隨機變量時，其求解的效率和準確性難以得到保障，在實際問題中應用效果不佳，而采用二元降維能有效地求解該高階矩陣，同時還能確保求解的準確性。式（9）的二維積分與一維積分的和通過二變量降維可以表達：

（10）

在上述公式中，0代表 n維零向量，表示去除掉第和個元素的零向量，代表零向量，第 j個元素被移除。例如，當n=3時，，，則，j=2，則；通過具有9個積分點的高階無跡變換，可將上述公式中的第一項表示為：

（11）

根據計算經驗可以將積分點與權重表示如下。

第一類點：

（12）

第二類點：

（13）

第三類點：

（14）

在式（10）等式中，第2項是一維的積分，并且可用三點高斯—埃爾米（Gaussian）積分來直接地解決：

（15）

到這里，可以總結出兩個變元降維函數計算的統計矩的步驟：

（1）按照在高次無跡化轉換中要求的標準值的積分點（標準值的分布變量），由反推得到原始空間中的變量X。

（2）在有限元軟件中，將（1）中獲得的隨機變量 X輸入，從而獲得一個功能函數響應點g（X）即；

（3）將所得響應值代入式（11）與式（15）中，求出二維和一維的積分。

（4）將一維和二維的積分結果，用式（10）代替，得到函數的統計矩陣的信息。

因此，在二元降維的基礎上，得到的統計矩陣可以表示為：

4. Pearson柔性系統分布法擬合概率密度函數

首先利用函數 Z的第一個二階統計量，把原變量 Z轉化成一個標準的正態分布Zμ=（Z-μz）/σz，相應地，Zμ的可能性的分布函數符合式（16）公式：

（16）

公式中的四個參數 a、 b、 c、 d都可以用 Z的斜度系數和尖度系數來表達，并且可以通過以下公式來確定：

（17）

（18）

（19）

（20）

其中，代表 Z的傾斜系數；代表峰值因子，在表1中給出了Pearson曲線群的公式。

表中參數（21）

K值可以由式（22）確定：

（22）

三、質量安全控制

（一）質量控制

預測水位時，在地下水建模過程中，應充分認識地下水復雜的環境和補徑排的特點，忽視某些對它有較大影響的因素，若干目標必須得以實現：數值模擬要反映研究區真實的水文地質狀況，每種邊界條件要與研究區的地下水流動趨勢和特性相一致，而含水層模擬要與研究區的實際地下水動力特性相一致。

根據實際建筑建立的有限元模型受到的荷載及約束條件與實際工程相同，能夠真實反映實際結果的受力及變形情況。在真實工作狀態下分析有限元模型后，所獲得的變形數據必須與測量結果比較，保證有限元模型的合理有效性。

在分析可靠性時，需要有大量準確的統計數據作為支撐得到隨機輸入變量的分布特點。例如，構件尺寸、材料屬性、水位分布等信息。得到的變量分布越接近真實，得出的事故發生概率越能反映真實情況，作為工程抗浮的控制依據越可靠。

（二）安全控制

在施工前，利用抗浮控制系統進行長期水位預測，獲得工程建設的全階段報警可靠性指數，并對工程建設的各個階段提出防浮措施。提供施工全周期的抗浮專項方案，做好應對事故發生的準備。

在施工過程中，針對短期的天氣預報和可能出現的極端惡劣天氣，預測短期水位，并獲得短期預警可靠度指數，為當時的施工階段提出預警和緊急處置措施，以減少或避免極端天氣引發的抗浮事故。

在施工時，利用計算機系統對現場發出施工指令，預測事故發生點，提出相應的抗浮控制應對措施，提前鋪設工作面，準備施工條件，避免事故發生后緊急施工造成現場混亂。

四、工程實例

（一）工程概況

本項目為長沙市某住宅小區的超大地下車庫，為在建項目，并且在施工過程中發生了抗浮失效事故。本工程的地下停車場為一棟二層鋼筋混凝土結構建筑物。在事故發生時，該停車場沒有做地基處理，頂部也沒有做過地基處理。該工程場地地面高度為38.5m，基坑底部的設計高度為31.5m。兩層樓高各3.8m。地下停車場占地27679m2，采用36m的防浮水平。該工程的西部緊鄰湘江，（地理位置大約為東經112°57′，北緯28°18′），是該區西部一條重要的河流；瀏陽河位于該工程的西北部，與湘江相接，地形從東南到西南，呈緩坡狀。具體各層構件信息見表2。

（二）基于FEFLOW的水位預測

首先驗證地下水模型的有效性，利用上述內容對停車場進行地下水水位預測。在FEFLOW中根據項目所在場地的地理位置、地形地貌、氣象氣候、河流水系、水文地質等條件分別進行地理信息數據轉換、初始條件及源匯項的確定、邊界條件及含水層的概化、水位地質參數的分區，建立場地的地下水數值模擬模型。分別建立該區域的地下水數值模型與項目場地的地下水數值模型，先初算得到項目場地的邊界條件，再以此為基礎計算項目場地的地下水流動狀態進而實現水位預測。地下水數值模擬模型如圖2、圖3所示。

結合工程具體狀況，在某年的5月1日至8月31日期間，這個地點發生了一次超大的降水。這一次的降水從6月22日到7月1日，共計10小時，而且這個時間內的降水量巨大，降水強度大。最大的連續降水量比1998年（歷史最大值）的降水量要大，6月30日8時～7月2日8時，在全市范圍內出現了特大暴雨，僅兩天的降雨量達到230.5mm，利用 FEFLOW軟件對5月1日至8月31日進行數值計算，期間以降水為主。所以將模型中的源匯項設定為一個隨著時間而改變的參數，時間順序如圖4所示，在所有的條件設定結束之后，就會模型運算。

將預測水位與實測水位值做對比，在模型中選取了32眼觀測井，其位置與現場觀測井的位置相同，并從32眼觀測井中均勻選取4眼觀測井，分別對實測的水位值及水位變化趨勢做對比。對比結果如圖5所示。

通過資料比較可以看出，每口測井的實際水位與模型的整體吻合良好，且模型的誤差很小。水位預測后，將預測的水位隨時間的變化數據進行K-S檢驗，得到水位分布的分布類型及統計參數用于可靠性計算。由長期的水位預測數據可以得到施工全周期過程中的水位分布，極端天氣變化后的短期預測可以得到短期內的水位分布用于短期預警。

對項目場地進行長期的水位預測，得到施工期不同階段的水位分布數據見表3。

（三）可靠性分析

對項目進行抗浮可靠性分析。在此基礎上，將相關的影響因子視為一個隨機的輸入變量，重點分析。結構的自重、混凝土和鋼筋的材料屬性、梁柱板等部件的尺寸等因素。在該結構中，對其產生影響的主要原因是在建設過程中，隨著建設的進行，其自身重量會變得更大，其效果具體體現為地下室底板所受到的水浮力的作用，可以從水位的預報中獲得分布數據，可以在查閱相關文獻和大量數據的測量和統計，從而獲得與之相同的標準值的材料屬性及部件尺寸等的變量統計特征，見表4。

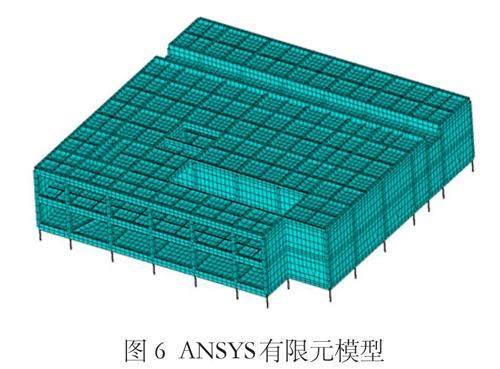
根據項目的工程概況，利用ANSYS有限元軟件建立該案例模型。其中，梁柱單元采用BEAM188單元，樓板單元采用SHELL63單元，抗浮樁采用BEAM188單元。建模時對地下車庫部分進行模擬，對側的主體結構用固定約束來替代主體結構，以確保主體結構對地下室起到限制作用，在樁的底部設置固定約束，模擬土層對樁的限制。圖6為有限元模型。

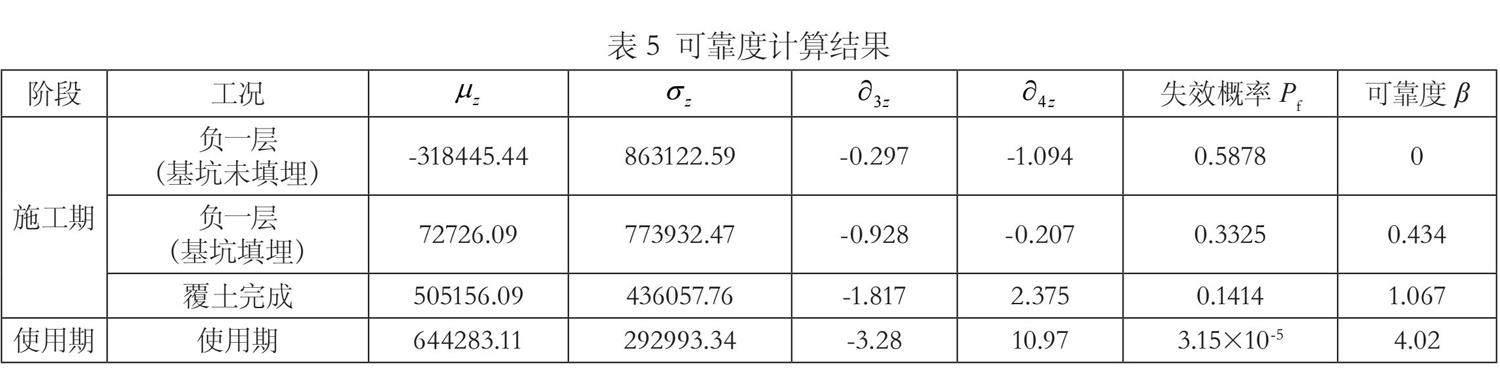
以高階矩法對該案例進行可靠性分析，把抗浮樁拉斷當作抗浮破壞的判據，也就是當一根抗浮樁的軸力超過了其極限承載能力時，就會被認為是結構抗浮破壞，這個問題在可靠度分析中表現為：取其最大軸力和其極限承載能力之間的差，作為一個隨機的輸出變量，稱為 Z，即，計算結果見表5。

本項目屬于2級安全級別，從表5中得到的計算結果可以看出，隨著建設的持續推進，可靠性會增強，失效的概率會降低，在3個不同的時期，可靠性的計算值比《建筑結構可靠度設計統一標準》（GB 50068—2018）中的3.7低，失效的概率會很高，容易出現抗浮破壞，在服役期間，可靠性的指數達到4.02，符合規范的規定，可靠性的分析也符合實際要求。在施工期，應根據可靠度指標的大小分別制定抗浮處理方案。在本項目中，對于負一層完工但基坑未回填，可靠度指標較小，應在結構底板受力最小的部位鉆孔泄壓，增設地表水匯入隔阻措施，并加強水位監測，基坑填埋之后，可靠度指標有所增大，但仍不滿足要求，應保持抽排水力度，執行增加配重的措施，加強水位監測密度達到每小時一次，并召開專家咨詢會，研究專項方案，覆土完成之后，加強水位監測密度至每天4次，做好后續措施的預備，在使用期時，可靠度指標滿足規范要求，可保持正常的水位監測，做好水位數據記錄。

五、總論

本文的研究相較于傳統的抗浮事故發生后的抗浮處理具有如下優勢：

（1）根據預測預警系統，優化處理結構的抗浮設計，優化建筑的抗浮措施，同時保證經濟效益與技術效益。

（2）在事故發生前預測事故可能發生的位置，提前做好施工應對方案，事故來臨前做好施工條件準備，優化施工人員、機械設備、材料等的投入，既可保證有序施工，又能最大限度地降低經濟損失。

（3）事故發生前的預測，做好抗浮措施，可以有效避免事故發生造成的安全問題，以及減少事故發生后需要的工程修復返工等費用的投入。

參考文獻：

[1]王海東，尹鵬宇，羅雨佳.超大地下結構施工期水位隨機分布抗浮可靠性分析與應用[D].土木工程與管理學報， 2022：039-002.

[2]連正.城市深部超大跨度地下空間施工力學特性與變形控制技術研究[D].西南交通大學，2021.