硫黃回收裝置停車期間SO2減排技術探討
瞿 楊 胡 超 陳 洪 許佳樂 唐興波 徐 飛
中國石油西南油氣田公司天然氣凈化總廠, 重慶 400021
0 前言
隨著中國環保要求越來越高,國家生態環境部正式發布GB 39728—2020《陸上石油天然氣開采工業大氣污染物排放標準》,根據硫黃回收裝置規模將天然氣凈化廠硫黃回收裝置尾氣中SO2排放濃度限制在 400 mg/m3或800 mg/m3,不再執行GB 16297—1996《大氣污染物綜合排放標準》、環函〔1999〕48號《關于天然氣凈化廠脫硫尾氣排放執行標準有關問題的復函》中的相關規定,天然氣凈化廠硫黃回收裝置自2023年1月1日起執行新規定,當硫黃回收裝置總規模≥200 t/d時,尾氣中SO2排放濃度限值<400 mg/m3(1 h平均值),硫黃回收裝置總規模<200 t/d時,尾氣中SO2的排放濃度限值<800 mg/m3(1 h平均值)。硫黃回收裝置不管是在日常運行過程中,還是在開停車期間,尾氣SO2都將執行更加嚴格的排放要求[1]。
1 除硫的目的和意義
天然氣凈化廠硫黃回收裝置在正常生產過程中,催化反應段中的H2S、SO2發生克勞斯反應生成單質硫,主要以S6、S8為主的形態存在。隨著裝置長周期的運行,部分硫蒸氣會冷凝在催化劑孔結構中,特別是采用低溫克勞斯硫黃回收工藝時,過程氣中的H2S、SO2在低溫克勞斯反應器中發生低溫克勞斯反應,生成的單質硫沉積在催化劑的空隙結構中,通過高溫過程氣對催化劑空隙中沉積的單質硫進行再生。但由于裝置低負荷、催化劑長時間運行磨損等原因,日常生產運行過程中存在再生不徹底等狀況,催化劑的空隙中仍然沉積有部分單質硫[2-4]。
因此在硫黃回收裝置停工或檢修前,需對反應器催化劑床層空隙內附著的單質硫和少量FeS進行清除,否則在裝置冷卻降溫的過程中,單質硫會附著在催化劑空隙中凝固,造成反應器催化劑床層堵塞,增加催化劑床層的壓差,引起硫黃回收裝置系統回壓升高,影響后續的檢修和裝置開車工作的順利進行。同時,隨著硫黃回收裝置運行時間的增長,H2S、SO2會腐蝕裝置設備管道,產生的FeS等物質存積在反應器催化劑床層中,FeS燃點較低,容易自燃引起催化劑床層中存積的單質硫燃燒生成SO2,造成尾氣SO2排放濃度的上升,加大了環保風險。且FeS在燃燒過程中放出大量的熱量,會導致反應器催化劑床層溫度過高,進而導致催化劑失去活性,嚴重時會損壞反應器等設備。因此在硫黃回收裝置吹掃降溫前,必須對反應器催化劑床層進行除硫操作,清除催化劑床層存積的單質硫、FeS等物質,確保檢修過程的安全,同時“復活”催化劑性能,以便下一次順利開車以及保持催化劑的活性,使硫黃回收裝置高效運行[4-6]。
2 除硫工藝存在的問題
目前硫黃回收裝置惰性氣體除硫工藝主要包括傳統燃料氣燃燒除硫工藝、熱氮除硫工藝、堿法煙氣脫硫工藝。
2.1 傳統燃料氣燃燒除硫工藝
硫黃回收裝置傳統的停車除硫工藝通常采用燃料氣等當量與空氣配比燃燒,由此形成高溫的惰性過程氣,對催化劑床層沉積的單質硫進行氣化,硫蒸氣隨著高溫的惰性過程氣一并進入硫冷凝器進行冷凝回收,達到催化劑性能“復活”的目的,燃料氣燃燒除硫工藝流程見圖1。在燃料氣燃燒除硫過程中存在以下兩方面問題。

圖1 傳統燃料氣燃燒除硫工藝流程圖Fig.1 Flowchart of traditional fuel gas combustion desulfurization process
2.1.1 除硫熱惰性氣體流量小
在停車除硫期間反應器催化劑床層升溫過程中,燃料氣和空氣配比燃燒形成的熱惰性氣體流量較小,對催化劑床層和空隙中沉積的單質硫升溫速度及除硫效率不高。在硫黃回收裝置停車期間為了除硫徹底,只能增加除硫時間(除硫時間通常在120 h以上),導致硫黃回收裝置的檢修時間延長。對天然氣凈化廠正常生產期間設計酸氣流量、空氣流量、停車期間主燃燒爐燃料氣流量和降溫蒸汽流量統計見表1。

表1 天然氣凈化廠正常生產期間設計酸氣流量、空氣流量、停車期間燃料氣流量、降溫蒸汽流量統計表
由表1可見,硫黃回收裝置停車階段燃料氣等當量燃燒過程氣量遠遠低于正常生產運行期間酸氣與空氣配比后的過程氣量。
2.1.2 除硫期間尾氣SO2排放濃度波動大
由于天然氣凈化廠停車初期,脫硫單元停止進原料氣后,溶液系統存在部分富液,需繼續對富液再生。再生出來的H2S等酸性氣體會繼續進入硫黃回收裝置,此時硫黃回收裝置處于燃料氣與酸氣混燃的狀態,無法精確控制空氣、酸氣、燃料氣流量配比,導致此階段硫黃回收裝置SO2排放濃度波動大[4-5]。
隨著富液量的減少,脫硫單元進入硫黃回收裝置的酸氣流量越來越少,同時酸氣組分變化越來越大,再加上燃料氣燃燒期間空氣流量減少導致的流量計計量不準確等因素,更加大了硫黃回收裝置配風的難度。如果配風不足,會造成燃料氣不完全燃燒,帶來反應器催化劑床層積炭的風險;如果配風過多,系統中存在過剩氧,造成催化劑床層超溫,過程氣SO2排放濃度增加且大幅波動,增加尾氣外排超標的環保風險[7-8]。
以某天然氣凈化廠硫黃回收裝置為例,由于停車期間過程氣流量減少,整個反應器催化劑床層升溫時間長,特別是反應器催化劑床層四周升溫速度慢,除硫時間長。同時由于催化劑床層存積部分FeS,在過氧初期階段,尾氣SO2排放濃度均有所上升。2020年6月16日至19日正常運行期間和19日至27日除硫期間尾氣流量、SO2排放濃度波動情況見圖2。
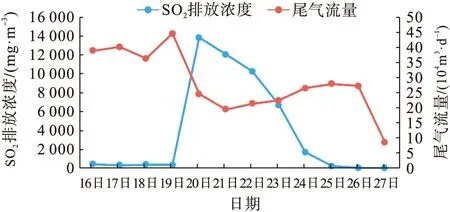
圖2 2020年6月某天然氣凈化廠硫黃回收裝置停車期間尾氣流量與SO2排放濃度波動趨勢變化圖Fig.2 Tail gas flow and SO2 emission fluctuations duringshutdown of sulfur recovery unit at a natural gaspurification plantplant in June 2020
2.2 熱氮除硫工藝
利用惰性氣體氮氣不與克勞斯系統內硫黃、硫化亞鐵、硫蒸氣及其他物質發生化學反應的原理,在硫黃回收裝置停工期間,采用熱氮氣對硫黃回收裝置反應器催化劑床層進行除硫,減少停車除硫過程中尾氣SO2排放濃度波動,確保硫黃回收裝置停車過程中平穩運行。
中國石化北京化工研究院齊魯分院開發了熱氮除硫停工工藝,使用熱氮取代傳統的燃料氣燃燒形成高溫惰性氣體進行除硫,在催化劑床層空隙中硫單質氣化清除完成后,主燃燒爐補入少量氧氣,對硫黃回收裝置進行過氧鈍化操作,在此過程中,需要消耗大量的氮氣,以滿足熱氮除硫工藝的需要[4]。
天然氣凈化廠在燃料氣與空氣等當量燃燒過程中,為了增加整個除硫過程中過程氣的流量,在主燃燒爐爐頭加入了部分氮氣,但是凈化廠空氮系統的處理量有限,在凈化廠裝置停工過程中,脫硫脫水裝置吹掃需要大量的氮氣,導致氮氣流量不足,無法滿足持續增加氮氣流量來增加過程氣流量的要求,所以利用氮氣作為惰性氣體除硫不能滿足目前硫黃回收裝置停工除硫的要求。
2.3 堿法煙氣脫硫工藝
堿法煙氣脫硫工藝主要用于硫黃回收裝置尾氣SO2脫除,該工藝利用各種堿性吸收劑或吸附劑捕集煙氣中的SO2,吸收產物為Na2SO3、Na2SO4并隨廢水排放,從而達到降低尾氣SO2排放濃度的目的。由于生成含Na2SO3、Na2SO4廢水排放至污水處理裝置后,天然氣凈化廠設計的污水處理工藝和容量對含Na2SO3、Na2SO4廢水處理困難,需增加對應的污水處理工藝,加大了污水處理裝置的運行成本和難度[9-12]。
3 解決措施
3.1 嚴格按照風氣比進行配風操作
在硫黃回收裝置停車前,應對燃料氣、空氣、降溫蒸汽流量計進行校驗,確保燃料氣、空氣、降溫蒸汽計量準確。在硫黃回收裝置停車時,隨著脫硫單元酸氣流量逐漸減少,酸氣組分波動較大,酸氣切換燃料氣混燃期間需及時調整配風量,嚴格按照2∶1在線分析儀的指示調整配風量,防止配風量過少,過程氣中H2S過多,引起尾氣SO2排放濃度波動,同時燃料氣不完全燃燒出現析炭會造成催化劑床層空隙積炭,影響催化劑活性。待酸氣流量為0,主燃燒爐完全切換為燃料氣燃燒時,嚴格按照燃料氣空氣等當量燃燒進行配風,確保燃料氣完全燃燒放熱,形成高溫的熱惰性氣體,對反應器催化劑床層空隙中的單質硫進行脫除[10,13-14]。
3.2 摻配吹掃氮氣增加過程氣流量
在燃料氣等當量燃燒期間,當空氮系統氮氣處理量足夠充足時,可在主燃燒爐爐頭增加摻入吹掃氮氣,通過主燃燒爐燃料氣燃燒對加入的氮氣進行加熱,增加過程氣流量和熱量,提高對反應器催化劑床層和空隙的除硫速率,同時由于氮氣為惰性氣體,可減少除硫期間尾氣SO2排放濃度波動[11-13]。
3.3 利用現有尾氣處理裝置對SO2進行堿洗
在硫黃回收裝置停車期間,尾氣將直接進入尾氣煙囪排入大氣,不再進入后續尾氣處理裝置進行處理,這樣可減少硫黃回收裝置除硫期間尾氣組分變化對尾氣處理裝置停車操作的影響。為了降低尾氣SO2排放濃度,對尾氣處理裝置進行技術改造,硫黃回收裝置停車期間的尾氣將繼續進入尾氣處理裝置,通過向冷卻系統或者清潔洗滌系統加入NaOH等堿性物質,對尾氣中的含硫化合物進行吸收,達到降低尾氣SO2排放濃度的目的,此過程中不需要對尾氣處理裝置增加堿洗塔等大幅度技術改造[15-21]。
3.4 對尾氣進行循環回收利用
硫黃回收裝置在停車階段,將進入尾氣焚燒爐焚燒排放的尾氣通過增壓后返回到主燃燒爐,回收的尾氣通過燃料氣與空氣配比燃燒后生成高溫煙氣,增大裝置過程氣的流量和熱量,高溫的過程氣再次進入反應器內對催化劑床層吹掃除硫和升溫,提高除硫效率和催化劑床層的升溫速率,該工藝對尾氣進行回收循環,可以增加硫黃回收系統除硫過程氣的流量,同時尾氣為惰性氣體,不會對反應器催化劑床層產生影響,可有效降低硫黃回收裝置停車期間尾氣SO2排放濃度波動[17]。
4 結論
1)天然氣凈化廠硫黃回收裝置在停車過程中采用傳統燃料氣燃燒除硫工藝存在一定問題,如:熱惰性氣體流量小,除硫效率低;燃料氣與酸氣混合燃燒期間酸氣組分波動較大,無法精確控制空氣、酸氣、燃料氣流量配比;燃料氣和空氣流量過小時導致計量不準確等。上述問題造成除硫期間配風困難,尾氣SO2排放濃度波動大。
2)為了降低尾氣SO2排放濃度,可以采取嚴格按照風氣比進行配風操作、摻配吹掃氮氣增加過程氣流量、利用現有尾氣處理裝置進行SO2堿洗、對尾氣進行循環回收利用等措施。尤其是利用尾氣處理裝置對SO2進行堿洗、循環回收尾氣中的熱惰性氣體等先進SO2減排工藝,不但可以降低尾氣SO2排放濃度,且不需要對硫黃回收和尾氣處理裝置進行大幅改造,工藝簡單,裝置投資和操作成本低,滿足環保要求的同時,可實現天然氣凈化廠節能、降耗、減排的目的,具有較好的經濟價值和環保效益。

