根升余弦脈沖成型正交相移鍵控信號關鍵參數估計
朱 航,宋 偉,譚 銘,呂海燕,戴 崢
(國防科技大學信息通信學院,湖北 武漢 430000)
0 引言
在數字調制傳輸中,相移鍵控信號(PSK)[1-2]應用廣泛,其利用載波的相位來攜帶數字信息,幅度、頻率恒定,但相位在碼元轉換時刻發生跳變。與幅度鍵控信號(ASK)、頻移鍵控信號(FSK)相比,相移鍵控信號具有抗噪聲性能好等優點。
在合作通信條件下,PSK信號的解調技術已經非常成熟[3],然而在非合作通信中,有別于傳統通信系統中的信號解調,由于缺乏通信信號的先驗知識,其解調屬于盲解調,需要通過通信偵察對載頻、符號周期等關鍵參數進行估計,為解調提供條件。盡管現有的載波相位同步[4-5]、符號定時同步[6-7]等技術能夠在未精確探明載頻、符號周期的條件下實現解調,但是在估計值與真實值差距較大時,難以快速達到同步狀態,造成誤碼率較高。因此,為實現可靠的盲解調,需要開發精度較高的參數估計方法。在以往的研究中,針對矩形脈沖成型的PSK信號參數的精確估計問題,已經有一些行之有效的方法[8-9],然而實際通信中升余弦脈沖成型波形是更常見的情況,此時由于滾降系數的影響,在一定程度上增加了參數估計的難度,特別是在低信噪比條件下影響了估計精度。
本文以根升余弦脈沖成型正交相移鍵控(QPSK)信號為研究對象,探討了包括載頻、符號周期、滾降系數在內的多個關鍵系數估計方法,旨在為信號的盲解調提供條件。
1 信號模型
QPSK信號數學模型如下:

(1)
式(1)中,sk=ak+jbk∈{1,-1,j,-j}是第k個符號周期內所傳輸的符號值,T是符號周期,f0是載頻,φ0是隨機相位,且g(α,T)(t)是根升余弦脈沖,滾降系數為α,其數學表達式為

(2)
式(2)說明信號經過根升余弦脈沖成型。接收信號可以表示為
r(t)=s(t-τ)+v(t),
(3)
式(3)中,τ是一個未知的接收延遲(為便于說明,假設0≤τ r[n]=r(nTs)=s(nTs-NτTs)+v(nTs), (4) 由于涉及到的待估計參數較多,為了快速完成估計過程,對于Nr點接收信號先進行粗估計。首先按長度L將其分為等長的多段,而后通過信號分段頻譜取平均獲得信號功率譜的估計: 圖1 關鍵參數粗估計原理圖Fig.1 Rough estimation principle of key parameters 信號包絡可以表示為 將其重寫為 |s(t)|2=u1(t)+u2(t), (10) 其中: 對其中的u1(t)進行傅里葉變換得到 (11) 式(12)中,C{·}表示Chirp-Z變換。 進而得到 對QPSK信號進行載頻估計的常用方法是通過四次方譜進行,然而在較低信噪比的條件下,對接收信號進行四次方處理會極大地加強噪聲,造成載頻所對應譜線被淹沒在噪聲中。因此,在本文中,先對信號進行奇異譜分析[10]消弱噪聲,而后對消噪后的四次方信號進行Chirp-Z變換,實現低信噪比條件下的載頻精確估計。 對接收信號進行4倍的重采樣,得到ru[n],而后構建其漢克爾矩陣: 假設對接收信號去載頻后,經過接收根升余弦濾波處理,滾降系數為αr: (17) 而后,對信號在合適的采樣點處取值: 圖2 滾降系數估計原理Fig.2 Estimation principle of roll-off factor (24) (25) 本章給出一個估計實例,并對本文方法估計性能進行分析。 設接收到的QPSK信號符號周期為T=1 μs,載頻為f0=1.51 MHz,幅度為A=0.5,滾降系數α=0.35,接收延遲為τ=0.6 μs,初始相位隨機,信噪比為SNR=-5.1 dB,采樣率為fs=10.25 MHz,真實值NT=10.25,Nτ=6.15。 需要說明的是,在通信系統中,一般以比特信噪比SNRb=Eb/N0來衡量性能,由于其與信號信噪比SNR之間滿足下述關系: (26) 式(26)中,Nbits-per-sym為每符號所攜帶的比特數。根據上述關系式,計算出此時比特信噪比SNRb=2 dB。 圖3 仿真過程示意圖Fig.3 Schematic diagram of simulation process 圖4 符號周期及載頻估計誤差曲線Fig.4 Estimation error curves of symbol period and carrier frequency 圖5 延遲量及滾降系數估計曲線Fig.5 Estimation curves of time delay and roll-off factor 圖6給出了在不同比特信噪比條件下對信噪比及幅度的估計誤差曲線,可以發現在對信噪比及幅度進行估計時,信號長度的影響并不明顯。盡管這兩項參數不是最為關鍵的參數,但是對它們進行估計有利于信號處理。例如,由于信噪比估計不依賴于任何已估計參數,在得到信噪比估計值后,結合功率譜估計出的符號周期粗值,得到對比特信噪比的粗略估計,而后根據圖4所展示的估計精度分析圖,可以選擇合適的信號長度進行精確估計。而對幅度的估計有利于基于估計出的參數實現信號的盲解調。 圖6 信噪比及幅度估計誤差曲線Fig.6 Estimation error curves of SNR and amplitude 本文提出了非合作通信中根升余弦脈沖成型QPSK信號關鍵參數估計方法。該方法基于功率譜分兩步對參數實現估計,即先“粗估計”再“精確估計”,利用功率譜及其直方圖實現對載頻、符號周期的快速粗估計,在此基礎上根據包絡譜特點利用Chirp-z變換估計得到符號周期的精確估計值,引入奇異譜分析方法在信號去噪的基礎上實現載頻精確估計,利用載頻及符號周期的精確估計值實現對滾降系數的估計,并給出對信噪比和信號幅度進行估計的方法。從仿真分析結果看,本文所提方法有利于根據粗略估計值確定合適的信號長度,以保證在較低的信噪比條件下具有足夠的關鍵參數估計精度。盡管本文主要以QPSK信號為研究對象,提出了相應的方法,但是仍然能夠經過適當改進以實現對其他進制PSK(如BPSK)信號的參數估計。2 參數估計方法
2.1 基于功率譜的參數粗估計
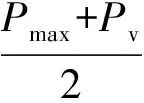
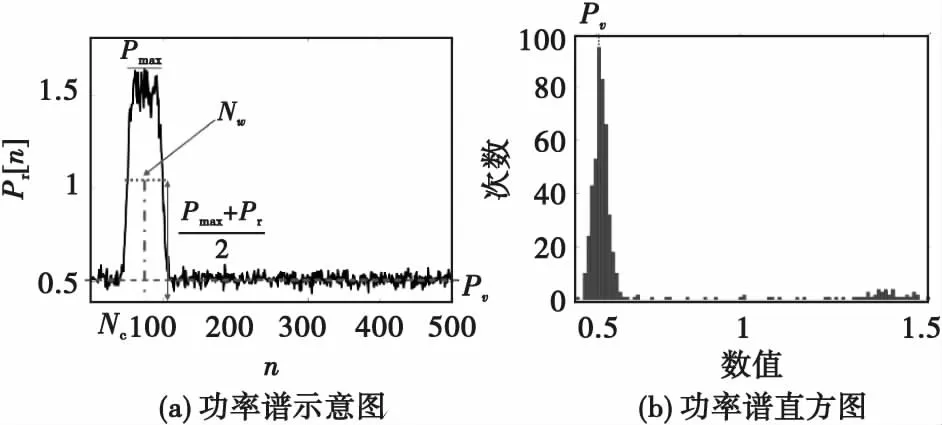
2.2 基于包絡譜分析的載頻精確估計
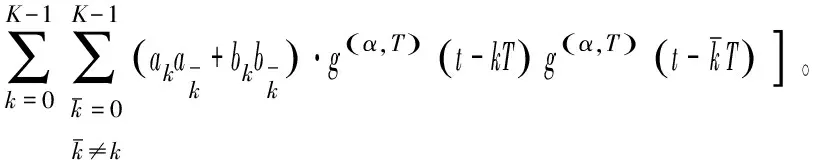
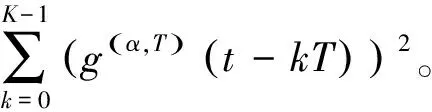
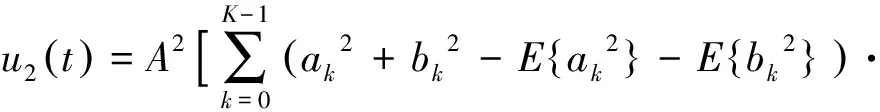


2.3 基于奇異譜分析去噪的載頻精確估計

2.4 滾降系數估計
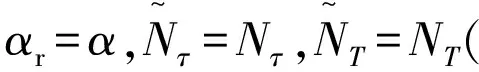
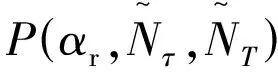
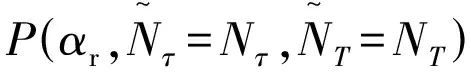
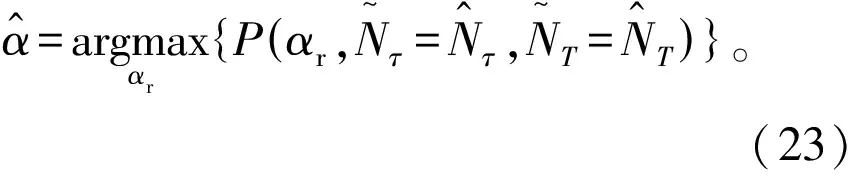
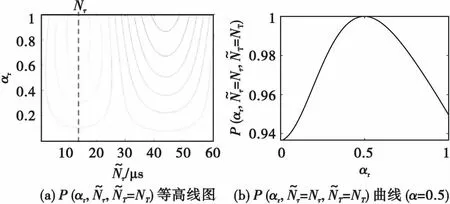
2.5 信噪比及幅度估計
3 仿真與分析


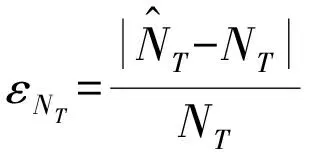

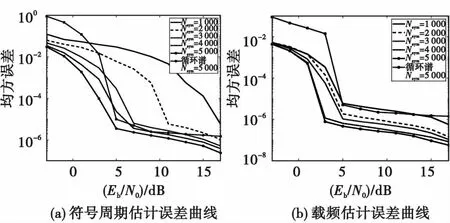


4 結論

