鹽沼生態系統中植物和硫化物相互作用模型的穩定性分析①
尹甜, 喻鳳斯, 黃啟華
西南大學 數學與統計學院,重慶 400715
在許多生態系統中普遍存在空間自組織模式,如干旱生態系統、淡水與鹽沼系統、珊瑚礁等等.實驗和理論模型都強調這些自組織模式可以揭示驅動生態系統復原力的潛在機制,因此有利于幫助我們推斷生態系統的環境變化.在鹽沼系統中植被模式的空間動力學行為受多重因素影響,例如養分消耗、硫化物積累和毒性都是制約鹽沼植被發育的因素.另一方面,研究表明植物的生長會促進土壤中硫化物的濃度增長.受文獻[1]的啟發,主要對鹽沼系統中植被與硫化物相互作用的機理進行研究.我們首先考慮一個描述植物和硫化物相互作用的常微分方程模型,分析平衡點的存在性、局部[2-5]和全局穩定性[6-9],獲得植物和硫化物共存的條件以及導致植物滅絕的條件等.接下來考慮到植被和硫化物的空間擴散[10-15].我們將常微分方程模型延伸到反應擴散方程模型,進一步分析擴散對常數穩態解的影響.研究結果表明擴散系數不影響常數穩態解的局部和全局穩定性,即不會產生圖靈不穩定性.最后,我們用數值模擬驗證理論分析的結果.
1 常微分系統的穩定性分析
考慮如下植物-硫化物的反饋模型:
(1)

為便于對模型(1)進行理論分析,我們引進以下無量綱化的變量和參數:
則模型(1)可以無量綱化為
(2)
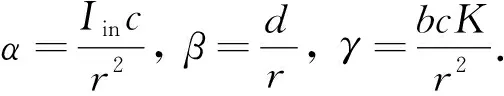

為了分析平衡點E0和E*的穩定性,我們在平衡點處對模型(2)進行線性化得到對應的Jocabi矩陣為
于是在E0處,
在E*處,
因此

于是,我們有以下定理:
定理1(i) 當β<α時,模型(2)只存在一個邊界平衡點E0,且E0是局部漸近穩定的;
(ii) 當β>α時,模型(2)存在兩個平衡點E0與E*,其中E*是局部漸近穩定的,E0是鞍點.
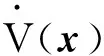

內除平衡點外,不再包含系統的其他軌線,則模型(2)的平衡點是漸近穩定的.于是為了討論正平衡點E*的全局穩定性,可取Liapunov函數

因為
(3)
將1-p*-s*=0,α+γp*-βs*=0代入(3)式得
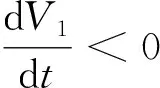
2 偏微分系統的穩定性分析
接下來考慮到植物和硫化物的空間擴散,我們將常微分方程模型(2)延伸至如下的反應擴散模型:
(4)
其中:p=p(x,t),s=s(x,t)分別代表t時刻x處的土壤中植物的密度和硫化物的濃度,dΔp和Δs分別代表植物和硫化物的擴散速率,其中Δ是拉普拉斯算子,Ω?R是邊界光滑的有界域,模型(4)的第三個方程表示Neumann邊界條件,υ是邊界?Ω上的單位外法向量,模型(4)的第四和第五個方程表示植物和硫化物的初始分布,p0(x)和s0(x)都是Ω上的連續函數.
設0=μ0<μ1<μ2<…是Ω上考慮Neumann邊界條件時算子Δ的特征值.
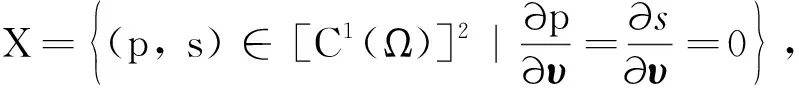
定理2(i) 當β<α時,模型(4)的常數穩態解E0是局部漸近穩定的;
(ii) 當β>α時,模型(4)的常數穩態解E0是不穩定的.
證在E0處對模型(4)進行線性化,有
其中
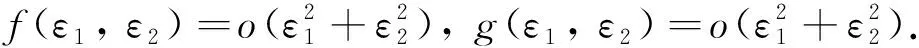
Xi是不變子空間,并且μi是L在Xi上的特征值當且僅當λi是矩陣Mi的特征值,
于是
從而


[tr(Mi)]2-4det(Mi)>[tr(Mi)]2>0
則
定理3當β>α時,模型(4)的常數穩態解E*是局部漸近穩定的.
證對模型(4)在E*處線性化,有
其中
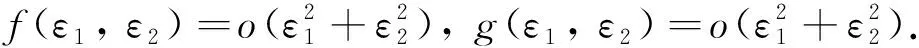
Xi是不變子空間,并且μi是L在Xi上的特征值當且僅當λi是矩陣Mi的特征值,
于是

(i) 若[tr(Mi)]2-4det(Mi)≤0,則
(ii) 若[tr(Mi)]2-4det(Mi)>0,則
因此L的特征值都具有負實部.
為了討論模型(4)正解的全局穩定性,需要給出以下引理.
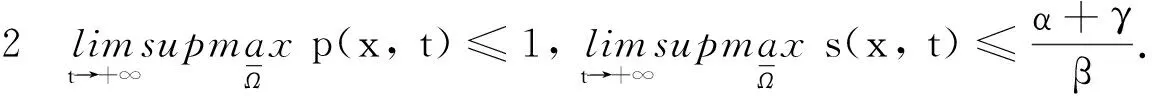
證考慮模型
(5)
設(p(x,t),s(x,t))是模型(4)的正解,p1(x,t)是模型(5)的解,于是由比較原理可得
0
接下來考慮常微分系統
(6)
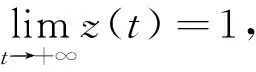
定理4當β>α時,模型(4)的常數穩態解E*存在并且是全局漸近穩定的; 當β<α時,模型(4)的常數穩態解E0是全局漸近穩定的.
證構造Liapunov函數
由分步積分公式以及Neumann邊界條件,得
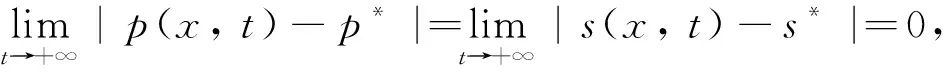
3 數值模擬
取參數α>β與α<β時模型(2)與模型(4)平衡點穩定性的情況如圖1,2所示.
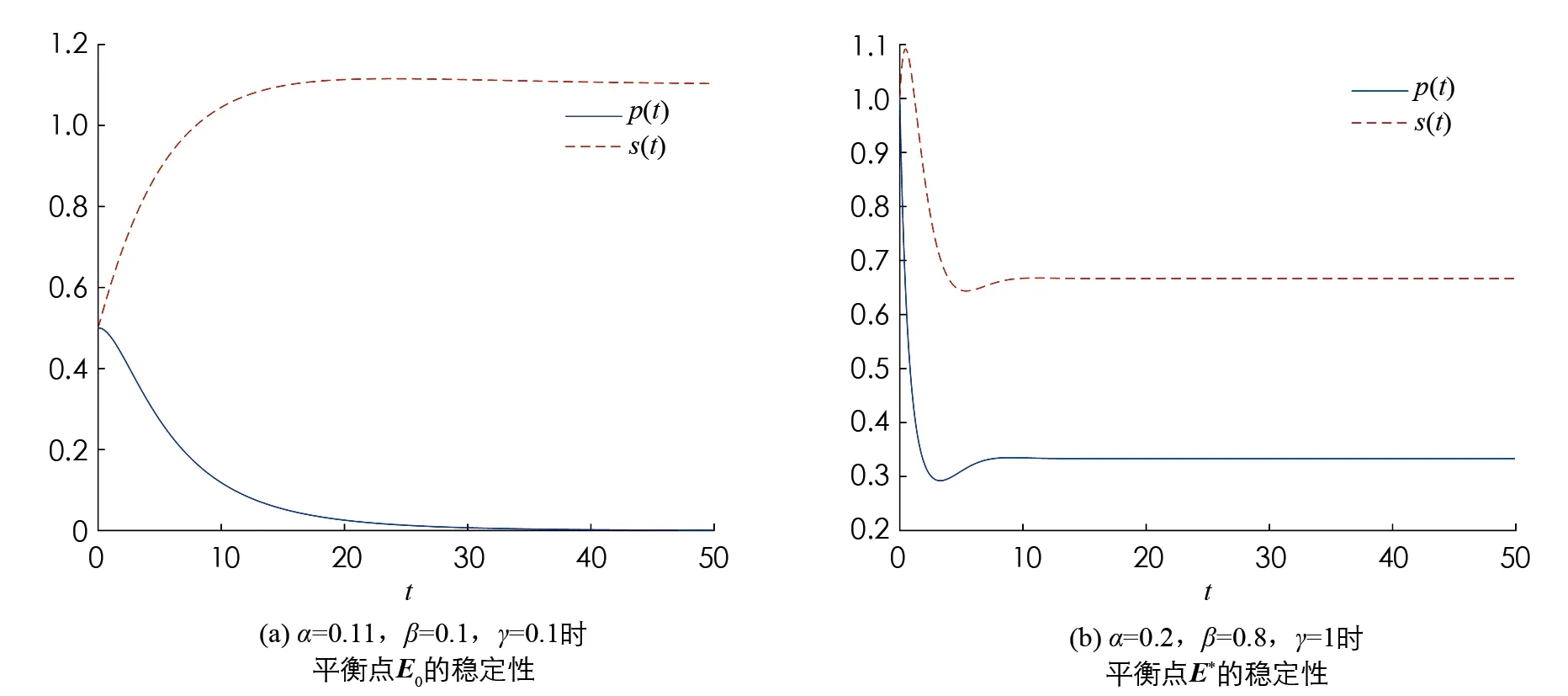
圖1 模型(2)平衡點的穩定性
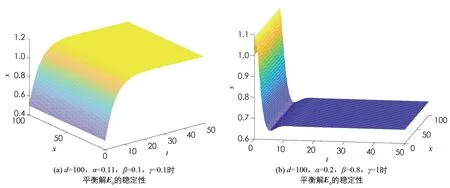
圖2 模型(4)平衡解的穩定性
由圖1可知當α>β時,模型(2)的平衡點E0是全局漸近穩定的; 當α<β時,模型(2)的平衡點E*是全局漸近穩定的.由圖2可知取d=100,當α>β時,模型(4)的常數平衡解E0是全局漸近穩定的; 當α<β時,模型(4)的常數穩態解E*是全局漸近穩定的.
4 結果與展望
本文在文獻[1]的模型基礎上稍有改動,考慮的是植被呈Logistic增長,硫化物濃度升高受土壤中硫化物的沉積以及植物的促進兩方面的影響.研究結果表明該模型的正平衡點在有無擴散的情況下都是全局穩定的,而植被的生長受多種因素的影響,因此研究營養物質與植被生長的關系也是十分有意義的.

