總縱彎矩作用下的船體結構極限承載力分析
車金枝
(山西應用科技學院建工學院,山西太原 030062)
0 引言
船舶作為海上運輸的工具,在海上航行過程中會遇到極端天氣影響,導致船舶顛簸、傾斜,且船舶通常運載十幾甚至幾十萬噸的貨物,受到海浪沖擊,船體的總縱彎矩會發生變化[1–2],進而使船體結構的極限承載力發生變化。當其極限承載力達到極值時,區域船體結構會出現斷裂現象,嚴重威脅船舶安全航行,因此研究船體結構的極限承載力對船舶安全航行非常重要。有很多學者研究船體結構極限承載力分析方法,丁仕風等[3]提出船體結構強度分析方法,該方法使用有限元構建船體結構模型后,在有限元環境中模擬冰荷載情況下的船體結構極限承載力。梅佳雪等[4]從船舶腐蝕角度出發,研究其結構極限承載力。雖然上述2種方法均可有效得到船舶結構的極限承載力,但在不同應用環境下,這2種方法均存在適用性不佳情況。為此本文提出總縱彎矩作用下船體結構的極限承載力分析方法,以提升船體結構極限承載力計算精度,為船舶維護提供有效數據。
1 船體結構的極限承載力分析方法
1.1 船體結構有限元模型構建
在分析船體結構的極限承載力時,需使用有限元構建船體結構模型,該模型構建流程如圖1所示。利用有限元軟件構建船體結構流程為:先將船體結構參數輸入到有限元模型內,生成船體解耦型材庫和肋位線庫。然后拾取結構網格線并處理網格劃分線后,生成船體結構平面網格交點[5],再以肋位線庫內數據為基礎,計算船體結構平面網格交點坐標后[6],生成三維幾何模型數據。對型材庫內數據賦予屬性后,生成有限元模型數據,至此得到船體結構有限元模型。
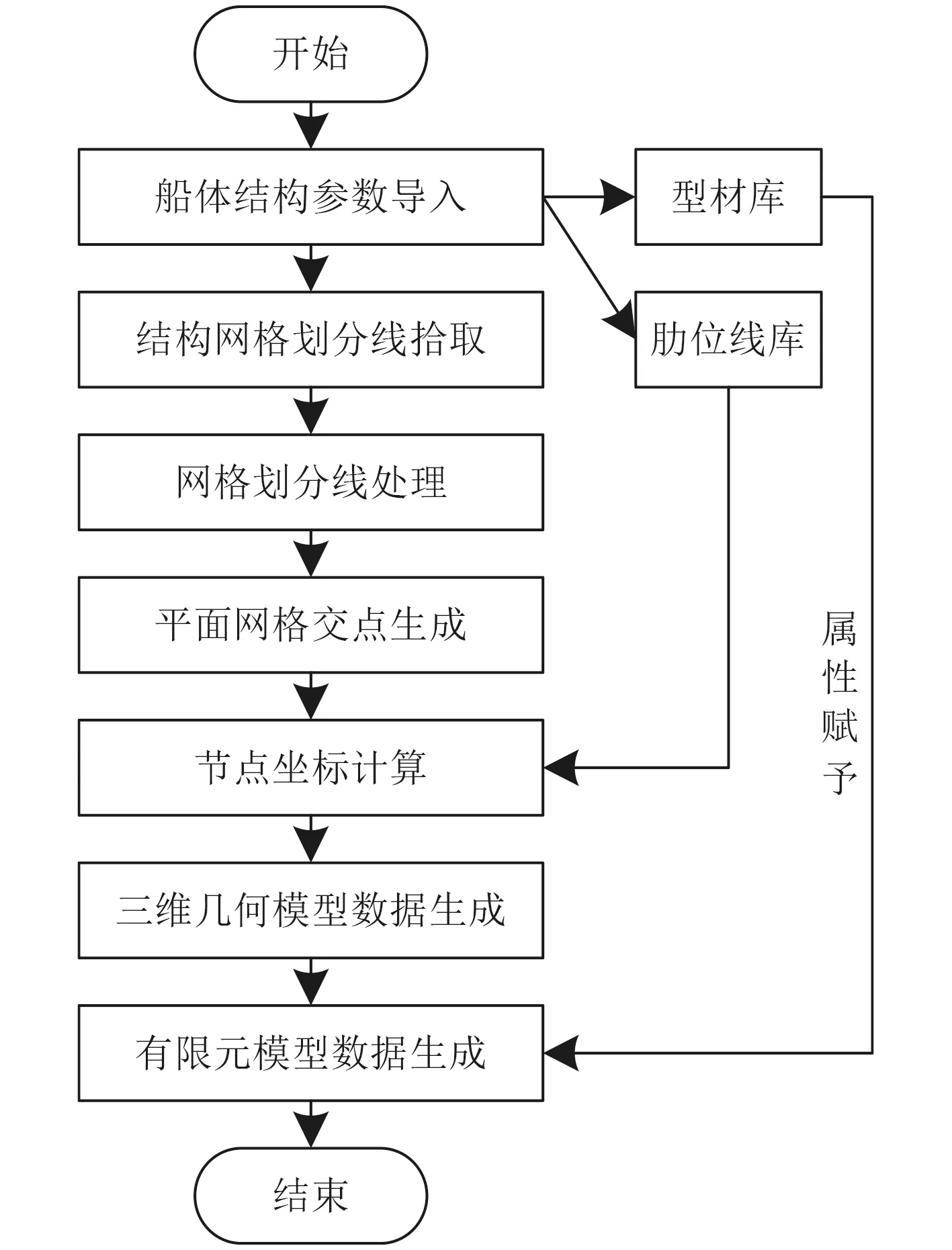
圖1 船體結構有限元模型構建流程示意圖Fig.1 Schematic diagram of building process of finiteelement model of hull structure
1.2 船體結構總縱彎矩計算方法
船體結構縱向不受軸向應力作用,因此其縱彎力矩計算公式如下:
式中:Wi為船體結構縱彎力矩;n為船體結構構件總數,且i∈n; ζi,Ai分別為構件應力值和剖面積;Ii為構件厚度。
船體結構板構件的應力值為其應變量函數[7],其表達公式如下:
式中, εi為船體結構板構建應變函數,其結果為板結構的應變量,該應變量與船體結構總彎曲曲率和中性軸位置關系如下:
式中: ?為船體結構縱彎曲曲率;y0為中性軸位置;yi為構建上下位置坐標。
以上述公式結果為基礎,構建船體結構總縱彎矩狀態方程g(t),表達公式如下:
式中:Qst,Qwt分別為靜水彎矩和垂向波浪彎矩。利用該公式即可得到船體結構總縱彎矩數值。
1.3 船體結構的極限承載力分析模型
為方便分析船體結構承載力[8],將船體結構有限元模型進行簡化處理,利用一維截面梁模擬船體結構,將船體劃分為n個肋位,其肋間距為L為一維截面梁長度。當船體結構總縱彎矩發生變化時,船體結構梁體的撓度微分方程為:
式中:y′′為船體結構梁體撓度微分方程;EI為船體結構肋位剛度。
利用有限差分方法求解式(5),將其微分問題轉換成代數方程問題,則船體結構梁的有限差分方程為:
式中:s為積分常數;EIi為第i個肋位剛度。通過求解式(6)即可得到船體結構撓度極限承載力。
從船體剖面平衡角度,分析總縱彎矩作用下,船體結構極限承載力。
?κH為水平曲率增量,?κV為縱向曲率增量,?MH為船體結構水平彎矩增量,構建總縱彎矩下,船體結構剖面平衡方程如下:
式中:?MV為縱彎矩增量;?κH為水平曲率增量;?κV為縱向曲率增量;RH,RV分別為縱向、垂向的抗彎抗彎剛度;RHV為結構的總抗彎剛度;E為船體結構材料的彈性模量;Ue為船體結構的單元有效截面積;yi,zi分別為相對于參考坐標,第i個船體結構單元的水平和垂直坐標;yG,zG分別為剖面受總縱彎矩后,其瞬時形心水平和垂向坐標。其中船結構單元有效截面積計算公式如下:
式中:U′為船體結構單元截面積; η為有效截面積縮減因子,其計算公式為
經過上述步驟,依據船體結構剖面平衡方程,可得到結構抗彎強度承載力數值。
2 實驗分析
以某遠洋船舶作為實驗對象,該船舶主尺度和中橫剖面參數如表1所示。
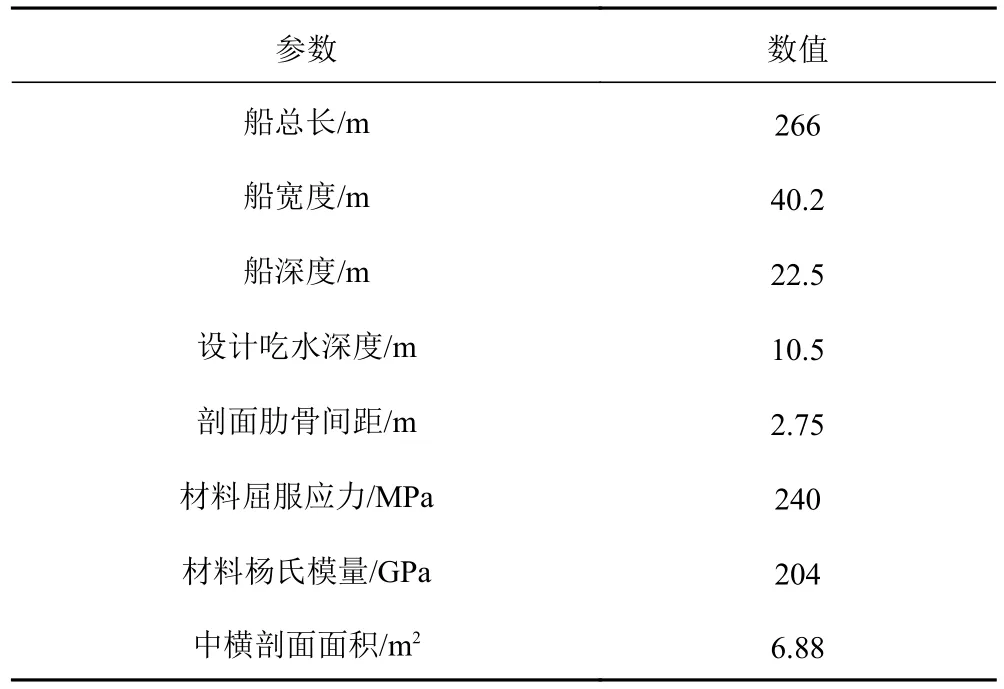
表1 船舶主尺度和中橫剖面參數表Tab.1 Parameters of ship's main dimensions and midsection
依據表1內船舶主制度和中橫剖面參數,建立船舶有限元模型,結果如圖2所示。分析可知,本文方法構建的船舶有限元模型較為逼真,且船體中部界面區域可利用不同顏色標注,在模擬其在總縱彎矩作用下,船體結構的極限承載力可更加清晰呈現給用戶。綜上結果,本文方法構架船舶有限元模型能力較強。

圖2 船舶有限元模型Fig.2 Finite element model of ship
在有限元軟件內模擬不同總縱彎矩情況下,分析船體結構單元平均應力變化趨勢,結果如圖3所示。分析可知,該船體結構單元的平均應力隨著總縱彎矩數值的增加先呈現指數式上升趨勢,再呈現迅速下降趨勢,說明當船體結構的縱總彎矩數值越大,船體結構的平均應力越小,也就是說此時船體結構的承載力逐漸趨于極限值。
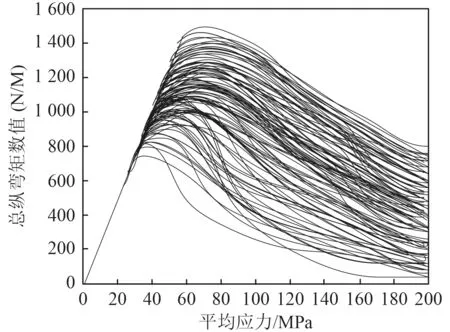
圖3 不同總縱彎矩情況下船體結構單元平均應力變化趨勢Fig.3 Changetrend of average stress of hull structural elements under different total longitudinal bending moments
在有限元內模擬該船體在從船體結構中截剖面在總縱彎矩為2 000 N/M 時,該船體結構中截剖面極限承載力分布狀況,結果如圖4所示。分析可知,當該船體結構受到2 000 N/M總縱彎矩時,其結構長邊外側的承載力數值較大,短邊中部位置承載力數值略低,長邊突出結構處,大部分結構顏色為黑色,說明其應力值為280 MPa,該應力值極為接近表1內,船舶材料屈服應力,說明該船體結構區域已達到極限應力值,存在較大結構屈服可能性。綜上結果,本文方法可有效分析船體結構總縱彎矩為2 000 N/M 時,結構的極限承載力,具備較好的應用效果。
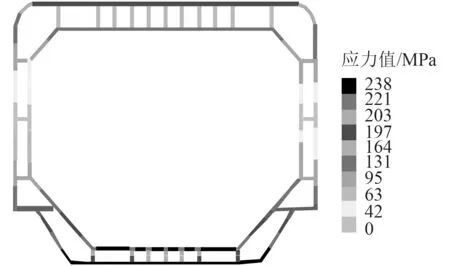
圖4 船體結構中截面剖面極限承載力分布圖Fig.4 Distribution diagram of ultimate bearing capacity of section in hull structure
以船體結構撓度承載力作為指標,使用本文方法模擬其在不同總縱彎矩情況下,船體結構撓度與總縱彎矩的曲線擬合關系,結果如圖5所示。分析可知,船體結構撓度承載力與總縱彎矩數值成正比例關系,但船體結構撓度隨著總縱彎矩數值增加,其數值增加較為緩慢。上述結果說明:當船體結構受到的總縱彎矩數值越大,船體結構的撓度數值也越大,但船體結構撓度數值呈現穩步增加趨勢。

圖5 總縱彎矩與船體結構撓度承載力擬合曲線Fig.5 Fitting curve of total longitudinal bending moment and hull structuredeflection bearing capacity
3 結語
船體結構的極限承載力分析對于船舶航行中維護來說非常重要,通過及時獲得船體結構承載力,對其結構承載力不足位置及時維護,可有效保障船舶航行安全以及貨物安全。本文方法將船體結構的總縱彎矩考慮其中,分析船體結構極限承載力,并對本文方法進行了多角度的驗證。驗證結果表明:本文方法分析船體結構極限承載力能力較為精準,具備一定的應用效果。

