工業攝影測量網形一致性對測量重復性精度影響研究

豆世豪，申 旭，宋志印，劉世濤，王新萍，黃桂平*

（1.華北水利水電大學 測繪與地理信息學院，鄭州 450046；2.河海大學 地球科學與工程學院，南京 210098；3.水利部水工金屬結構質量檢驗測試中心，鄭州 450052）

0 引言

中國首臺大型空間巡天望遠鏡計劃于2024 年發射升空，有望促進中國光學天文的飛躍式發展。空間望遠鏡光機桁架結構的形變對望遠鏡的觀測精度至關重要，因此對空間望遠鏡桁架進行真空中大范圍、高精度的形變測量必不可少，而工業攝影測量技術以其獨特的優勢成為完成這一任務的首選方式[1]。形變測量是指在一定條件下對被測物體進行周期性的重復觀測，以第1 次觀測結果為基準，將其他觀測結果與基準對比的差值作為被測物體的變形量，前提是必須保證測量單個工程的多次拍攝結果之間的精度。本文選擇工業攝影測量中的測量重復性精度作為精度評價指標[2-4]。

某空間望遠鏡的大尺寸桁架形變和應變場超高精度測量系統項目要求望遠鏡桁架形變的測量重復性精度達到5 μm 以內（6 m×5 m×5 m 空間范圍內），而目前國內外工業攝影測量系統在大尺寸空間范圍的測量重復性精度在15 μm 左右甚至更低[5-9]，無法滿足要求。為此，本文從工業攝影測量系統的硬件設備、軟件算法以及測量方法等方面進行研究、開發和改進，發現在硬件設備、軟件算法確定的基礎上，測量方法即測量網形的一致性對測量重復性精度的影響巨大。這一點在實際工程中容易被忽略，而且在已有的大量關于工業攝影測量網形的研究[10-13]中尚未找到關于測量網形一致性方面的研究報道。于是，本文在實驗室條件下使用機械裝置對測量網形一致性進行測試及結果分析，研究測量網形的一致性對測量重復性精度的影響，以期為其他航天器大尺寸桁架超高精度形變測量提供參考。

1 測量網形穩健性與一致性

工業攝影測量網形從幾何方面來講可以把每個相機攝站位置和被測物上的標志點（物方點）都看作是一個點，在測量時每個標志點至少要被2 個及以上的攝站所拍攝，如果將所有的攝影光線在圖紙上畫出，則各個攝站與單個標志點之間就形成了若干個三角形的網狀結構，如圖1 所示，這在測繪學中稱之為工業攝影測量網形[14]。

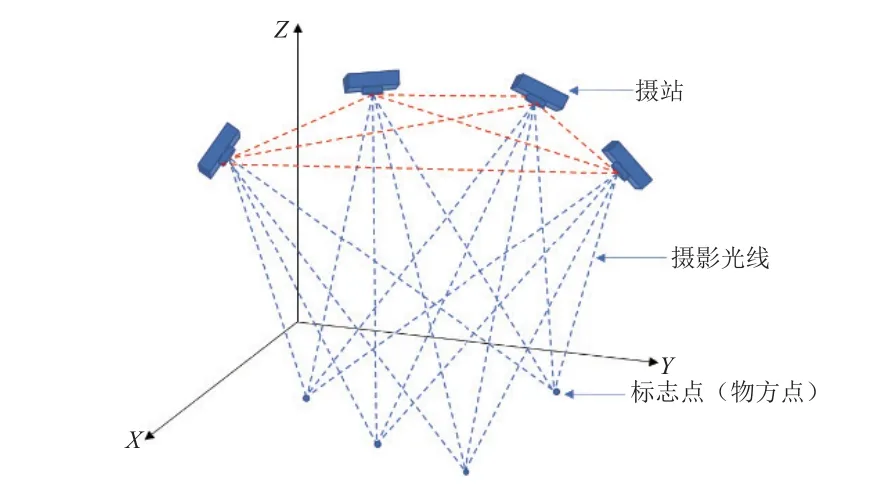
圖1 工業攝影測量網形Fig.1 Industrial photogrammetry network

在以往的測量網形研究中得出很多結論，如：在像點坐標精度一樣的情況下，測量網形布設不同，其測量結果的精度會相差10 倍等[15]，而通過改善測量網形中的攝站數量、像片重疊度、攝影距離、交會角以及標志點大小與分布等可提高測量精度。本文把以上諸多通過改變測量網形而影響最終測量結果精度的因素稱為測量網形的穩健性，其優劣以被測目標點坐標的標準差來衡量。測量重復性精度除了與測量網形的穩健性有關外，同時和多次測量間測量網形的差異程度的表征量也有很大關系，本文將2 次測量間網形差異的表征量稱為網形的一致性。

測量重復性精度要求在相同的測量網形下進行測量，即保證高的網形一致性。但在實際測量工作中，人員手持工業相機進行測量時不可能保證2 次測量過程之間的外方位元素參數（X、Y、Z、φ、ω、κ）完全相同，只能盡量保證其處在一定的可接受的變動范圍內。如圖2 所示，攝站A1、A2、A3、A4與攝站、、、均對被測目標進行相同拍攝測量操作，可解算得到測量重復性精度結果。但從嚴格意義上來講，這些測量結果已不能滿足重復性精度評價所需要的相同測量網形的要求，因此其得到的測量結果在一定程度上會使測量重復性精度變差。

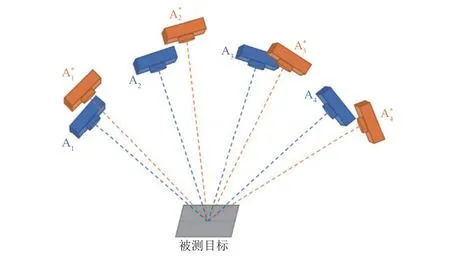
圖2 測量網形差異表示Fig.2 Difference of measurement network

2 網形一致性精度評價指標

相機姿態具有6 個自由度（6DOF）的參數，即3 個位移參數（X、Y、Z）和3 個空間旋轉參數（φ、ω、κ）。在工業攝影測量中，測量網形的一致性主要通過各組之間相同位置相機的姿態來反映，網形的一致性越好，其各組之間相同位置相機的姿態參數越一致，統計結果直接反映測量網形一致性的重復性和穩定性。計算時，首先在相同測量網形下對同一目標進行m組重復測量，每次測量采集n張像片，各張像片外方位元素分別表示為Xij、Yij、Zij、φij、ωij、κij（i=1, 2,…,m;j=1, 2,…,n）；其次求出m組之間外方位元素差值的絕對值，共=m(m?1)個數據，分別表示為ΔXuj、ΔYuj、ΔZuj、Δφuj、Δωuj、Δκuj（u=1,2,…,m(m?1)）；然后求出n張像片中外方位元素差值絕對值的標準偏差

最后，根據式(1)求u組外方位元素標準偏差的平均值

由式(2)得到的數據反映了工業攝影測量的測量網形一致性高低程度，與測量重復性精度評價一樣，得到的六自由度參數的標準偏差的平均值越小，表示測量網形一致性越好；反之，測量網形一致性越差。

3 試驗與結果

3.1 試驗概述

為探究測量網形變化對工業攝影測量重復性精度的影響，設計試驗進行探究。由于測量網形的穩健性對應于測量結果的精確度，而這是重復性精度的充分條件且已有許多實驗進行了驗證，本文將不再進行測試，而只關注于在測量網形穩健性優的前提下測量網形一致性對重復性精度的影響。

手持相機進行多組測量不能保證各組之間非常高的網形一致性，為此實驗室研發、采購了能夠控制測量相機六自由度姿態的移動框架和三維轉臺，并自主開發了操控軟件。本文將移動框架、三維轉臺、測量相機以及操控軟件這4 部分的組合稱為機械控制相機位姿拍攝裝置，其3D 模擬效果及測量現場分別如圖3 和圖4 所示，其中：移動框架測量精度優于1 mm；三維轉臺的測量精度優于0.01°；測量相機采用鄭州辰維科技股份有限公司的CIM-3 工業測量相機，分辨率為29 Mb，標稱精度為4 μm+4 ppm·L，設置曝光時間為600 μs、曝光強度為7。

圖3 機械控制相機位姿拍攝裝置3D 模擬Fig.3 3D simulation of the mechanically controlled camera pose shooting device

圖4 機械控制相機位姿拍攝裝置測量現場Fig.4 Test site of the mechanically controlled camera pose shooting device

3.2 試驗方案設計

本試驗使用機械控制相機位姿和人工設置相機位姿2 種方式，在實驗室內的測量相機精密檢校場（見圖5）上進行測量網形一致性的對比試驗研究。

圖5 測量相機精密檢校場Fig.5 Measuring camera precision inspection field

第1 步，使用機械控制相機位姿進行測量，稱為測量方式Ⅰ。如圖6 所示，測量相機按照5×5 測量網形、共25 個攝站對具有2500 個標志點的檢校場進行攝影測量。

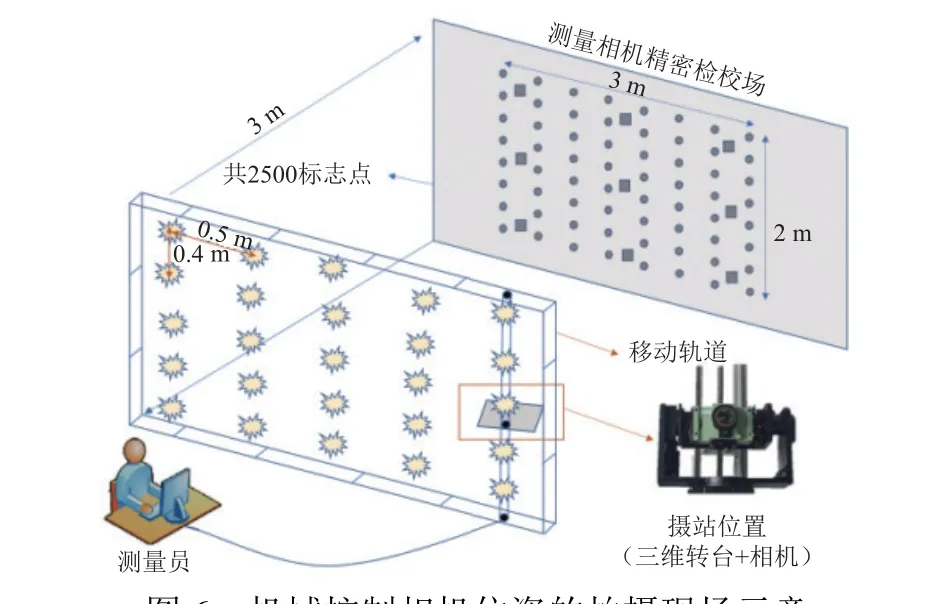
圖6 機械控制相機位姿的拍攝現場示意Fig.6 Schematic diagram of the shooting site for pose of a mechanically controlled camera

第2 步，人工設置相機位姿進行測量，稱為測量方式II。如圖7 所示，在地面做紅色位置標記，用于放置梯子進行拍攝，按照與第1 步相同的測量網形進行拍攝。

圖7 人工設置相機位姿的拍攝現場Fig.7 Shooting site for pose of a manually set camera

第3 步，地面無位置標記，在隨意位置按照5×5測量網形對測量相機精密檢校場進行人工測量，稱為測量方式Ⅲ。

使用軟件統計計算出以上3 種測量方式的攝站姿態的六自由度值，比對得出不同測量方式的網形一致性優劣；并對用這3 種測量方式所拍攝像片進行相關算法匹配、平差等過程數據處理，得出它們的測量重復性結果，分析網形一致性對測量重復性精度的影響。

3.3 試驗結果與分析

對拍攝像片進行軟件處理以及通過數學計算統計各個測量方式各組之間測量相機的六自由度姿態值的結果如表1 所示。3 種測量方式的測量重復性精度如圖8 所示。

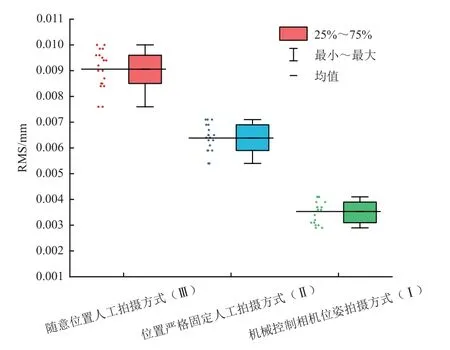
圖8 3 種測量方式的測量重復性精度結果Fig.8 Measurement repeatability accuracy results of three measurement methods

表1 3 種測量方式的相機六自由度姿態值對比Table 1 Comparison of six degrees of freedom attitude values for three measurement methods

從表1 給出的各組測量相機6 自由度姿態值可看出，機械控制相機位姿的測量方式Ⅰ明顯比人工控制的測量方式Ⅱ、Ⅲ得到的網形一致性精度要高，RMS 均值＜5 μm；從圖8 可看出，測量網形一致性越高，其測量重復性精度就越高，測量方式Ⅰ的測量重復性精度比測量方式Ⅱ、Ⅲ的至少提高了2 倍甚至更多。這些數據反映了在工業攝影測量系統中測量網形一致性對測量重復性精度的顯著影響。

4 結束語

工業攝影測量的測量網形可從穩健性和一致性2 個方面來描述。在網形穩健性優的情況下，保持盡可能高的網形一致性可顯著提高測量重復性精度，達到超高精度形變測量的目的。實驗室測量結果表明，通過機械控制多次測量之間的網形一致性，在測量相機精密檢校場測量時其測量重復性精度比日常人工測量提高了至少2 倍，達到5 μm 以內，滿足項目要求。本文研究結果可為空間望遠鏡桁架等大尺寸結構件的超高精度形變測量提供數據和技術支持。