基于改進的希爾伯特-黃變換的地震強震動特征提取

郭亞茹,豐繼華,楊黎薇,鐘玉盛

(1.云南省地震局,昆明 650224;2.云南民族大學,昆明 650031)

0 引言

近半個世紀以來,伴隨新出現時頻分析方法被不斷成功地應用于地球物理、環境科學和地質學等領域,現代時頻分析理論得到了長足發展。在信號頻譜研究和分析過程中,使用最多的是快速傅里葉變換(Fast Fourier Transform,FFT)。根據信號處理過程,可將以傅里葉理論為基礎的時頻分析方法歸納為三類[1]：第一類首先對信號加窗,其次進行傅里葉變換,前提條件為假設信號局部平穩,典型代表為STFT和Gabor變換等[2-3];第二類是直接更換傅里葉變換的基函數,典型代表為小波變換等[4-5];第三類是從信號中獲得雙線性函數,然后執行傅里葉變換,但存在交叉項的問題,如Winger-Ville分布等。

傅里葉分析的理論是將信號分解為正弦信號的加權和,當信號僅由幾個有限的正弦信號組成時,使用傅里葉分析是可行的,但如果信號沒有規律,使用傅里葉分解時需要大量的虛假的正弦信號去拼湊。此外,對于非線性分布的信號,始終存在來自交叉項的干擾。再者,受到不確定性原理的限制,傳統以傅里葉理論為基礎的時頻分析方法在時間和頻率分辨率并不理想,所以需要一種能自適應準確反映頻率隨時間變化規律的新方法。1998年,美國華裔科學家HUANG博士將經驗模態分解(Empirical Mode Decomposition,EMD)算法引入到希爾伯特變換中,提出了希爾伯特-黃變換(Hilbert-Huang Transform,簡稱“HHT”)。該方法被認為是近二個世紀應用數學領域中最重大的發現,一經提出,便受到了研究者們的普遍關注。

HHT旨在服務于非平穩和非線性信號分析,如在地震波分析、腦電波分析研究以及機械故障檢測等。在地震研究領域內,希爾伯特-黃變換的獨特性在于分析信號過程中不需要基函數[6-7],其基本原理是將原始信號自適應分解為多個本征模態函數(IMF),再將IMF進行Hilbert變換得出具有物理意義的物理參量。2001年HUANG[8]利用HHT對1999年集集地震中Tcu129地震臺站的加速度記錄進行分析,與短期傅里葉變換和Morlet小波分析相比,得到的希爾伯特譜能準確反映地震動能量的時頻分布;2003年ZHANG等[9]使用 EMD對地震波傳播進行研究;2009年劉強等[10]通過HHT變換計算結構地震反應的能量;2012年WANG等[11]運用EMD方法對地震信號進行時頻分析,證實了該算法的有效性;2016年梁岳[12]將改進HHT運用于儲層預測性能中。

本文選取了部分云南漾濞Ms6.4地震中不同震中距的強震動臺站所獲取的三分量加速度記錄數據,基于改進后的希爾伯特黃算法對其進行時頻分析,以不同角度客觀分析強震動的尺度和頻域特征。通過對實際地震動記錄進行特征提取后,獲取的希爾伯特時頻譜信號可清晰反映出強震能量隨時頻變化分布特征的能量譜,同時實現了時頻局部化的目的。與梁宏等[13]利用模態混疊問題及集合經驗模式分解方法(EEMD)分析九寨溝M7.0地震加速度記錄相比,本文改進后的模態混疊問題及集合經驗模式分解方法,彌補了其幅值系數不確定性的不足,其對地震強震動特征的提取過程可為類似破壞性淺源地震的強震動特征分析提供更有效的信息參數,為現代信號應用分析于強震動特征提供另一種新思路。

1 希爾伯特-黃變換的改進

1.1 引用數據來源

根據中國地震臺網正式測定,北京時間2021年5月21日21時48分,云南省大理州漾濞縣發生Ms6.4級地震,震中位于東經99.87°,北緯25.67°漾濞縣蒼山西鎮境內,震源深度為8 km[14]。地震共計造成了3人遇難,34人受傷,部分房屋破裂甚至倒塌,同時云南多地州有強烈震感。此次地震是云南繼Ms6.5魯甸地震和Ms6.6景谷地震后近10 a以來發生的又一次破壞性淺源地震。震中位于滇西北地區維西-喬后斷裂帶附近,震源機制結果顯示：此次地震是一次走滑型破裂事件,與區域構造特征一致。從地震序列的類型上可以看出：此次漾濞地震屬于“前震-主震-余震型”地震[15-18]。

云南地震局強震動臺網獲取強震動數據25組75條強震動數據(三分向記錄)。獲取強震動數據的25個強震動臺站,土層臺有23個,基巖臺有2個。按照國家強震動觀測常規數據的處理流程對25個臺站的記錄進行數據處理[19-21]。為了闡明提取記錄加速度特性效果,本文根據峰值加速度以及震中等因素,分別選取最具代表性的4個臺站：震中距為8.0 km的漾濞臺(YBX)、震中距為31.1 km的月溪井臺(DLY)、震中距為66.8 km的太和臺(BTH)、震中距為129.6 km的施甸臺(SDX)。其中：太和臺(BTH)為基巖臺。圖1為該地震中獲取加速度記錄的強震動臺站位置分布,具體記錄情況詳見表1。

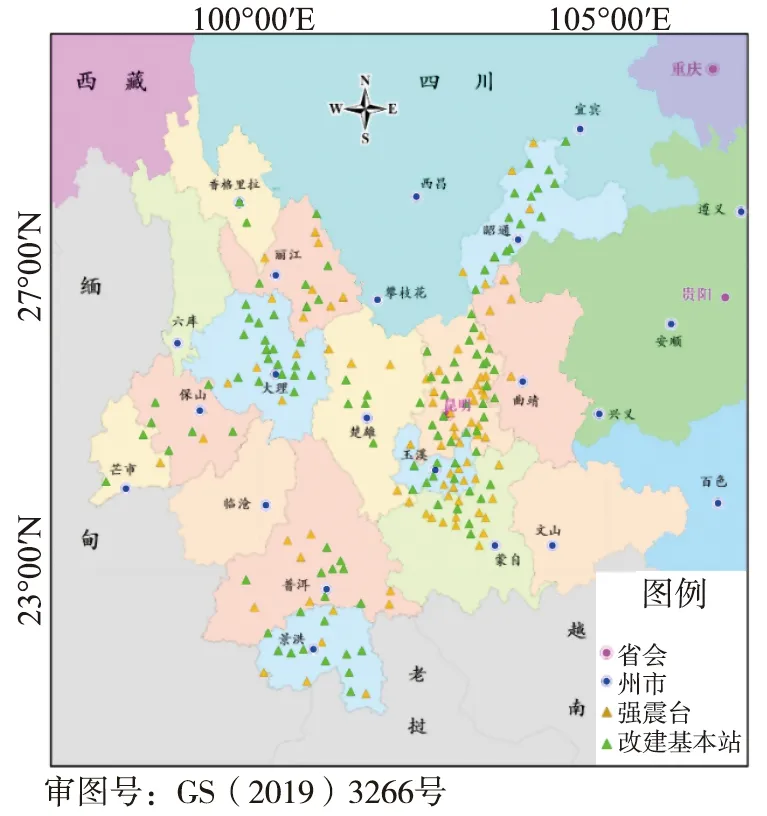
圖1 云南強震動臺站位置分布圖Fig. 1 Location distribution map of strong motion stations in Yunnan

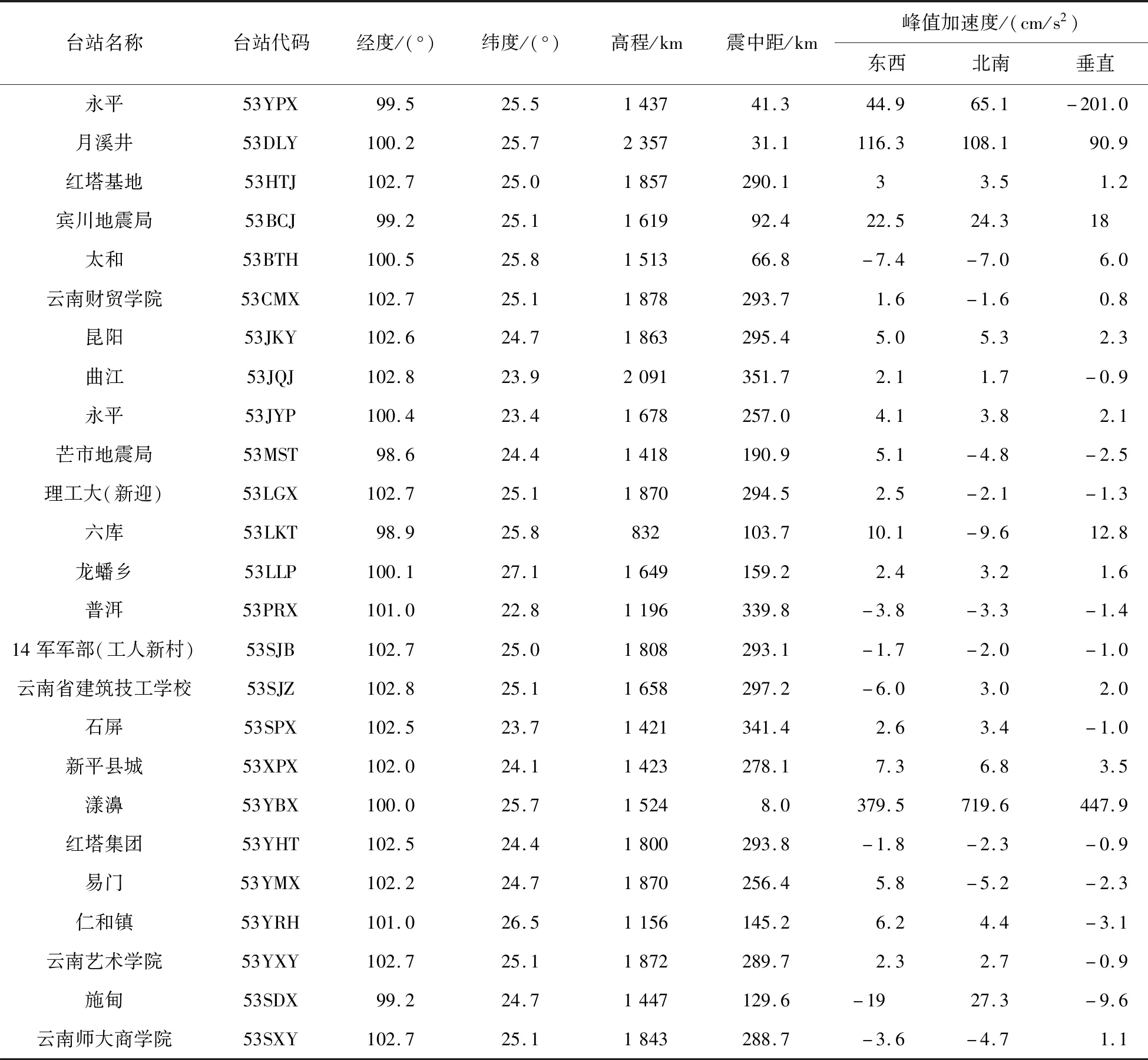
表1 云南漾濞Ms6.4強震動記錄Table 1 Ms6.4 strong ground motion records of Yangbi,Yunnan

1.2 希爾伯特-黃變換簡要概述

希爾伯特-黃變換(HHT)主要包含兩個部分：經驗模態分解(EMD)與希爾伯特變換(Hilbert transform)[22]。其原理為：先利用EMD方法分解原始信號得出本征模態函數,再將本征模態函數進行希爾伯特變換得出具有實際物理意義的參量。

1) 經驗模態分解(EMD)基本原理

EMD是希爾伯特-黃變換的核心步驟,可將原始混合信號分解為一系列本征模態函數(IMF)組件。EMD不同于快速傅里葉變換(FFT),其以原有信號為基礎直接進行分解,不需要基函數,適用于任意形式的信號,能夠應用于多種領域。EMD的分解過程一般基于以下條件進行：

(a)用于分解的數據信號是由幾種不同的本征模態函數(IMF)構成的,至少含有兩個以上的極值點。

(b)IMF同時具有線性與非線性的特點。

(c)如果數據信號沒有極值點只有拐點,可以利用二次或者多次求導取得極值,再進行積分。

EMD分解法是先通過尋找原始信號的極大極小值,分別取得極大值包絡mmax與極小值包絡mmin,再求其包絡均值m(t)[22]。設原始信號為x(t),h(t)為準模態函數,在第一次分解中的第一次篩分為：

m1(t)=(mmax(t)+mmax(t))/2

(1)

h1(t)=x(t)-m1(t)

(2)

如果第一次篩分結果h1(t)不滿足IMF定義,便開始第二次篩分,此時h1(t)作為被篩分信號重復以上過程,直到滿足黃鍔博士等提出的停止準則,即可跳出篩分循環,完成第一次分解,得到第一階本征模態函數c1(t),采用的停止準則為：

(3)

當Sd滿足0.2≤Sd≤0.3,即可跳出第一次分解,獲得第一階本征模態函數c1(t)：

c1(t)=h1k(t)

(4)

此時令：r1(t)=x(t)-c1(t)作為第二次分解的原始信號進行篩分循環：

r2(t)=r1(t)-c2(t),……,rn(t)=rn-1(t)-cn(t)

當rn為一個常數或者一個單調遞增(遞減)的函數再或者只含有一個極點的函數時結束分解,此時rn為剩余量,

(5)

在IMF生成過程中,EMD在每個時間段提取頻率最高的分量。因此,每個組成部分都不能間歇,否則,將發生模態混疊現象。

2) 希爾伯特變換(Hilbert transform)基本概念

假設本征模態函數x(t)的希爾伯特變換為?i(t),那么：

(6)

式中：P表示柯西(Cauchy)主值。根據這個定義,ci(t)和?i(t)形成一個復共軛對,可以得到一個解析信號zi(t)：

zi(t)=ci(t)+j?i(t)=ai(t)·ejθi(t)

(7)

式中：

(8)

式中：ai(t)為反映ci(t)能量隨時間變化的瞬時幅度,θi(t)為ci(t)的瞬時相位。而相位求導即可獲得瞬時頻率,如公式(9)所示：

(9)

原始數據x(t)(不包含余量rn(t))可表示為：

(10)

希爾伯特振幅譜H(ω,t)可表示為：

(11)

由希爾伯特振幅譜H(ω,t)進而獲得：邊際譜h(ω)和瞬時能量密度級IE：

(12)

(13)

3) 模態混疊問題及集合經驗模式分解(EEMD)原理

HHT最明顯的問題是由過包絡、欠包絡、模式混合以及干擾信號頻域特征提取的噪聲導致的模態混疊。集合經驗模式分解(Ensemble Empirical Mode Decomposition,EEMD)由HUANG等針對模態混疊現象提出的,其原理為：利用相位-幅度耦合方法來量化高頻帶和低頻帶之間的相互作用,分析獨立成份消除模態混合,改善每個本征模態分量的正交性[23]。

設x(t)為分析信號。EEMD的原理過程如下：

(a)信號xi(t)為：

xi(t)=x(t)+βω(i)(t)

(14)

式中：β為增加的白噪聲的方差,ω(i)(i=1,2,……)i是EMD傳導的數量,表示均值為0,方差為1的白噪聲。

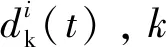
(c)計算每個最終的IMF：

(15)

4) 改進后的模態混疊問題及集合經驗模式分解(EEMD)原理及方法

模態混疊問題及集合經驗模式分解方法(EEMD)具有幅值系數不確定性,EEMD中EMD執行的總次數也是添加噪聲的次數為N,添加白噪聲的幅值系數為ε。WU和HUANG曾在論文中討論：幅度的選擇會直接影響分解效果,如果增加的噪聲幅度太小,其可能不會引入EMD所依賴的極端變化,如果增加的噪聲幅度太大,則分解結果可能不是原始數據,并且可能出現冗余IMF。根據算法提出的研究人員的建議與實驗經驗,建議在實驗過程中選用N=100,ε取值范圍為0.01～0.5較為合適。但是ε取值的具體情況應根據實驗中的具體情況而定,并沒有遵循某種特定的規則。

由此嘗試在兩個強震記錄的加速度信號中加入不同幅值系數(信噪比)的白噪聲,通過更改所加白噪聲的標準差觀察相關系數的變化,進而得出最佳標準差下最能消除模態混疊現象的白噪聲的分布。

在本文中,經過對比分析發現對于連續信號,正態分布信號,具有線性關系的信號,皮爾遜相關系數作為評判指標最為合適,當然用斯皮爾曼相關系數也可以,但是就效率而言沒有皮爾遜相關系數高。所以最終我們采用了皮爾遜相關系數,即ρX,Y定義為：

(16)

式中：cov(X,Y)是X和Y的協方差,σX為X的標準差,σY為Y的標準差,μX、μY分別表示X和Y的數學期望,所以相關系數可以表示為：

(17)

由圖2加入噪聲后的相關系數曲線可以直觀得到對于漾濞臺(YBX)、月溪井臺(DLY)、太和臺(BTH)和施甸臺(SDX)各個分量的最佳系數,選取結果即表2所列。為便于敘述將添加特定幅值系數白噪聲的EMD定義為AEEMD。為更為直觀比較EMD、EEMD與AEEMD分解效果,以太和臺(BTH)為例,對太和臺(BTH)EW向量進行分解,分別計算每種方法分解得到的各個IMF的方差σ與貢獻率mσ,以此作為模態混疊現象消除程度的評判標準。

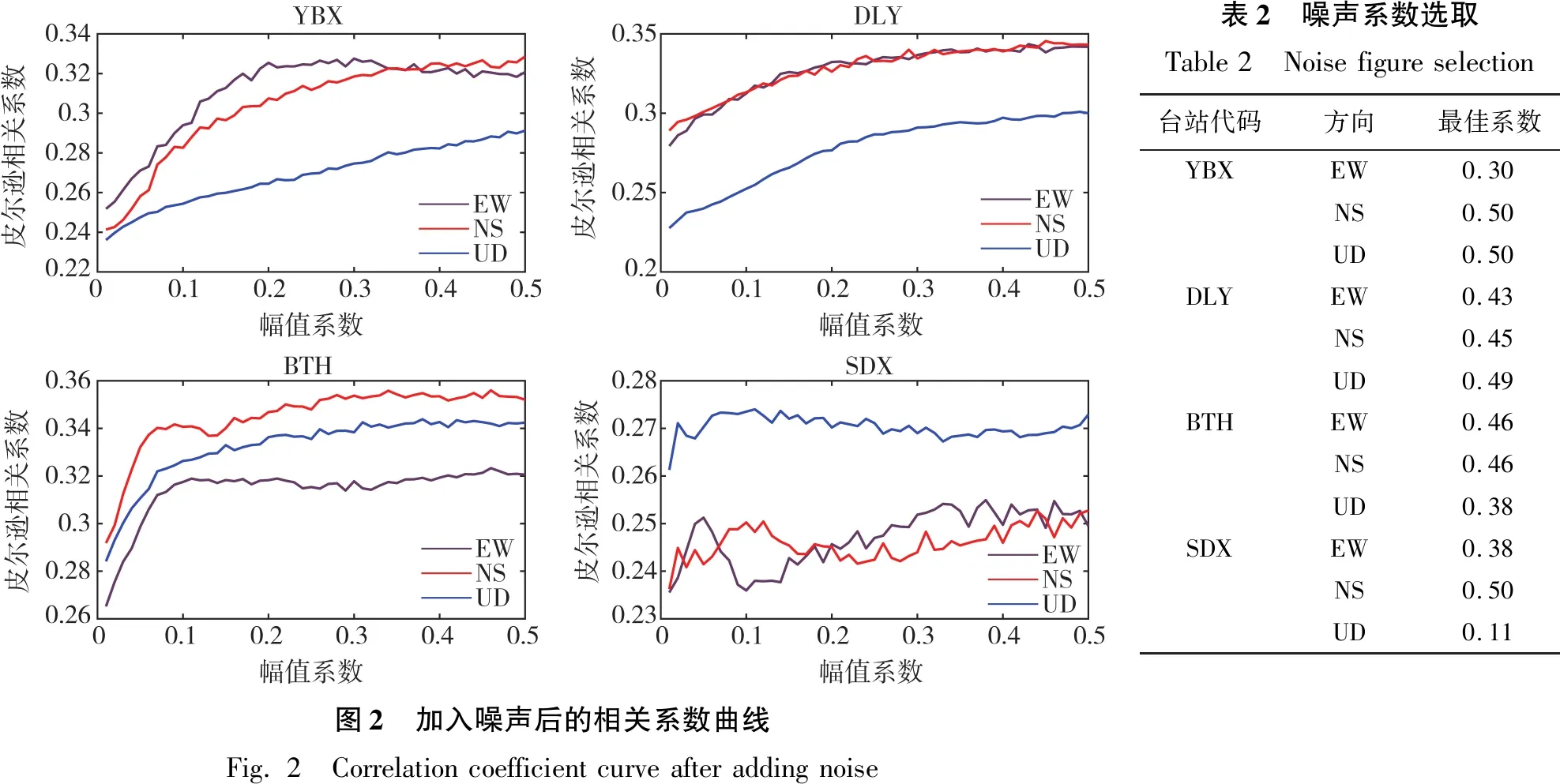
圖2 加入噪聲后的相關系數曲線Fig.2 Correlationcoefficientcurveafteraddingnoise表2 噪聲系數選取Table2 Noisefigureselection臺站代碼方向最佳系數YBXEW0.30NS0.50UD0.50DLYEW0.43NS0.45UD0.49BTHEW0.46NS0.46UD0.38SDXEW0.38NS0.50UD0.11

第k層本征模態函數ck(t)的方差σk為：

σk=E(ck(t)2)-(E(ck(t)))2

(18)

則第k層IMF的貢獻率為：

(19)

式中：σk與mσk越大說明所得IMF分量與原始信號最為相近,分解效果越好,反之效果則越差。分解效果如圖3、表3所示。

表3 三種分解方法中IMF的方差(BTHEW)Table 3 IMFs’ variance of three decomposition methods (BTHEW)

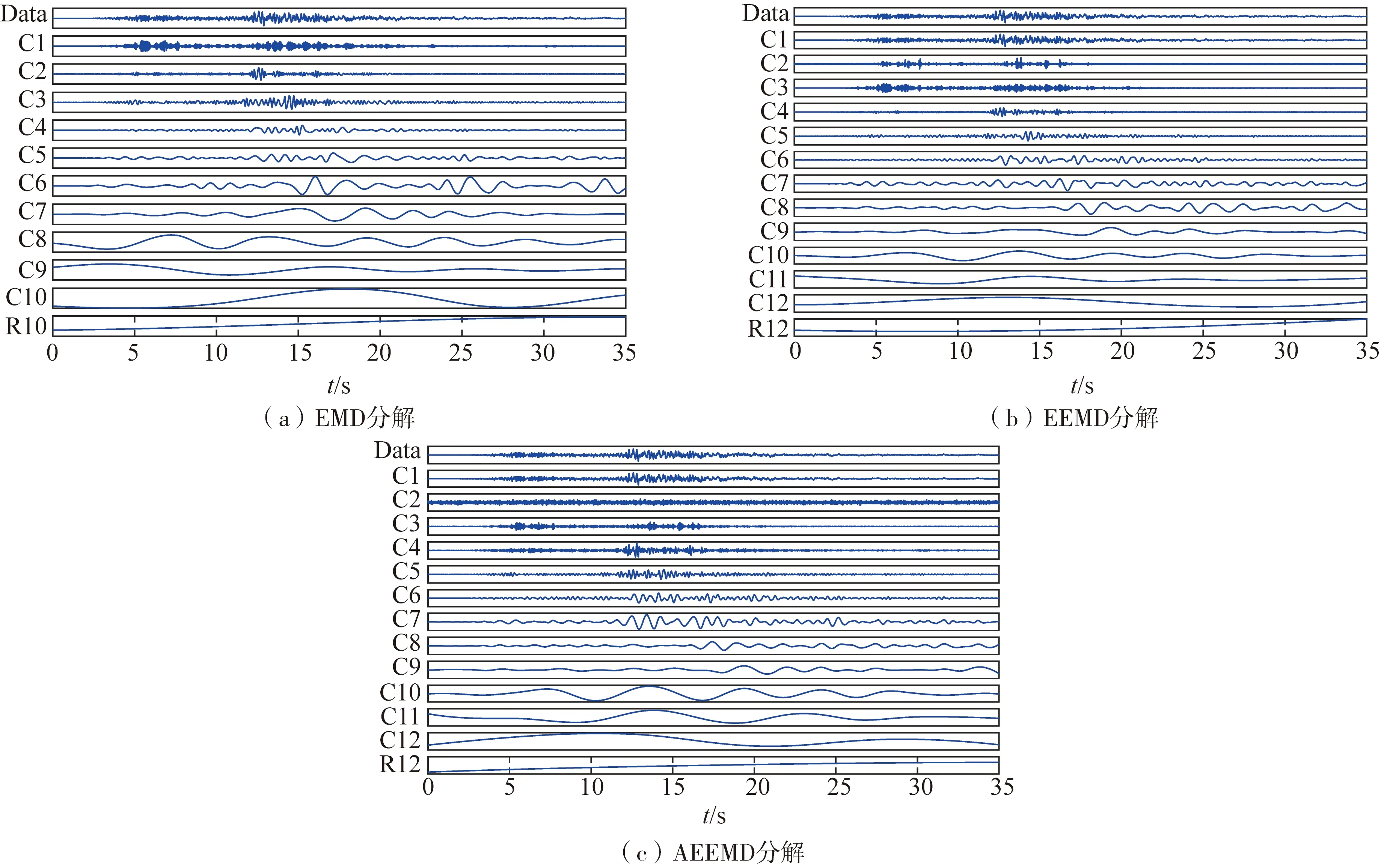
圖3 分解譜(BTHEW)Fig. 3 Decomposition spectrum(BTHEW)

圖3(a)為EMD分解結果,信號分為10層,圖中Data為原始信號,C1-C10為10層IMF,R10為分解10層之后留下來的殘余信息。從圖中可以看到IMF1到IMF10都包含原始信號,我們無法分辨哪個層具有最原始信號的信息。

圖3(b)為EEMD分解結果,添加根據算法提出的研究人員的建議與實驗經驗：100次幅值系數為0.2的高斯白噪聲。

圖3(c)為AEEMD即調整幅值系數為0.46后分解結果。

表3-表4所列為三種分解方法中IMF的方差與貢獻率。對于EMD方法：表3-表4均顯示IMF2的方差最大與貢獻率最高,僅從理論可知IMF1應與原始信號最為相近,因此最為合理的解釋為EMD方法出現了模態混合現象。對于EEMD方法：IMF1方差最大和貢獻率最高,應該具有原始信號信息最多,圖3(b)中IMF1與原始信號最為相似恰巧印證這一點。AEEMD方法同樣顯示IMF1方差最大和貢獻率最高,并且AEEMD中IMF1的貢獻率高于EEMD分解方法,所以AEEMD相較于EEMD更為突出的改善了模態混疊現象。

表4 三種分解方法中IMF的貢獻率(BTHEW)Table 4 IMFs’ variance of three decomposition methods (BTHEW)

上述實驗表明：添加的白噪聲幅值系數與所分解數據有關,只有添加適當的白噪聲,才可以最大程度改善模態混疊現象,提高分解的準確性。

2 特征提取

Hilbert-Huang變換(HHT)類似于傅里葉變換,兩者均是將時域中的信號進行解析,以便于頻域分析。在此,我們用希爾伯特-黃變換對強震動加速度進行分析：一是彌補傅里葉變換在信號時頻特性提取中的不足;二是通過HHT量化提取信號能量的時頻分布特征。

2.1 時域分解特征

圖4表示經過改進后希爾伯特黃變換之后的漾濞臺(YBX)、月溪井臺(DLY)、太和臺(BTH)和施甸臺(SDX)各個分量的三維采樣點-IMF層數-幅值譜,圖形將4個臺站每分量的采樣點-IMF層數-幅值進行了立體展現,從圖中可以看出：在任意一層本征模態函數均存在不同的頻率成分,各頻率成分的幅值(即其的相對含量)也不盡相同,與每個IMF分量對應的瞬時頻率之間往往沒有明顯的界限;區別于小波分析中頻帶必須嚴格劃分,并且隨著震中距的逐漸增大,每個本征模態函數的振幅波峰差距逐漸減小,而基巖臺加速度記錄相對更為平穩。獲取的希爾伯特時域譜信號可清晰反映出強震能量隨時頻變化分布特征的能量譜,同時實現了時頻局部化的目的,為類似破壞性淺源地震的強震動特征分析提供更有效的信息參數。

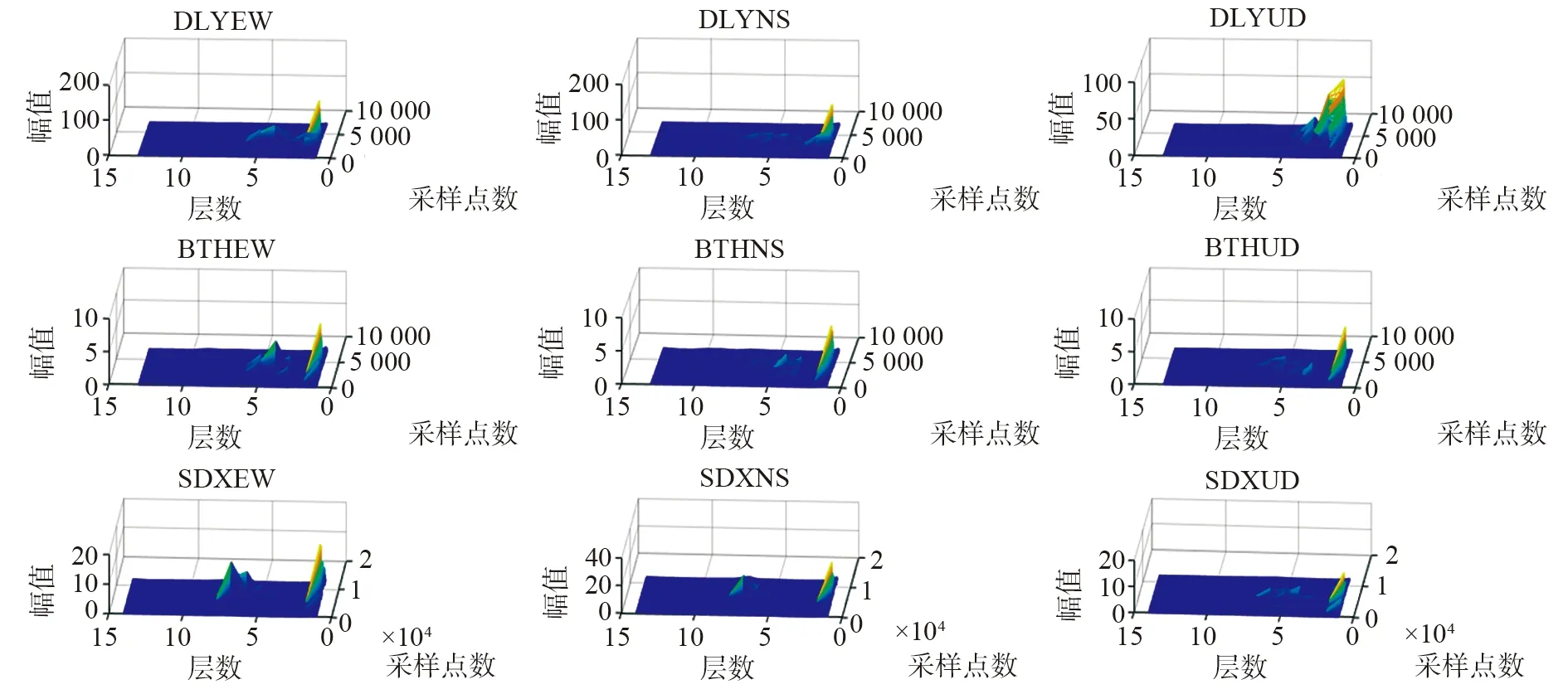
圖4 三維采樣點-IMF層數-幅值譜Fig. 4 3D sample point-IMF layer number-amplitude spectrums

2.2 Hilbert邊際譜分析

圖5是經過改進希爾伯特黃變換后得到的漾濞臺(YBX)、月溪井臺(DLY)、太和臺(BTH)和施甸臺(SDX)各個分量的邊際譜與FFT譜歸一化后的對比圖。以YBXEW為例,圖5 YBXEW為漾濞臺東西分量處理結果,震中距為8.0 km。對比FFT 譜和HHT邊際譜可以直觀發現：FFT譜在低頻時會低估信號幅值,而在高頻時放大信號幅值。漾濞臺(YBX)其他兩個分量(北南向NS、垂直向UD)、月溪井臺(DLY)三分量(東西EW、南向NS、垂直向UD)、施甸臺(SDX)三分量(東西EW、南向NS和垂直向UD)同樣印實了這一點。

圖5 Hilbert邊際譜與傅里葉譜對比Fig. 5 Comparison of Hilbert Marginal Spectrum and Fourier Spectrum

對比4個站點Hilbert邊際譜與傅里葉譜可以發現：隨著震中距的增加,最大地震動的峰值加速度出現明顯的衰減,而加速度記錄的主頻分量也出現相應增加。與梁宏等[13]利用EEMD分析九寨溝M7.0地震加速度記錄相比,抑制模態混疊現象效果更為突出,經本文改進過的希爾伯特黃變換所得到的Hilbert邊際譜與傅里葉譜對比圖,更為清晰刻畫出在震中距影響下FFT譜對信號低頻低估高頻放大現象的變化：隨著震中距不斷增加FFT譜與邊際譜差異性逐漸變小。

2.3 Hilbert變換與譜分析

圖6為經過改進希爾伯特黃變換后得到的漾濞臺(YBX)、月溪井臺(DLY)、太和臺(BTH)和施甸臺(SDX)三分量的譜分析結果二維顯示,其中太和臺(BTH)為基巖臺,另外三個為土層臺,時頻譜橫坐標為頻率,縱坐標為HHT的瞬時能量,圖像顯示了能量分布特征：當震中距為50 km以內時能量集中于20 Hz左右,隨著震中距的增大,最大加速度峰值出現急速衰減,能量的分布規律也顯現出特定形態。聯系時域分解特征與邊際譜特征分析,該方法在強震記錄數據處理時頻分析方面展現了特有的實效性。

圖6 HHT時頻譜二維顯示Fig. 6 2D HHT spectrums

3 結語

本文選取了云南漾濞Ms6.4地震中不同震中距的強震動臺站所獲取的三分量加速度記錄數據,采用了基于改進后的AEEMD算法對其進行時頻分析。通過分析可知：

1) 該方法可在保證信號分解穩定性的同時,抑制模態混疊現象。通過本文對強震動數據的分析擬合,不但成功將加速度數據分解為本征模態函數,還獲取了希爾伯特時頻譜信號。

2) 本文獲得的邊際譜可更加準確的反映信號的實際頻率成分,更適于處理非平穩信號。

3) 本文獲得的能量譜可清晰反映出強震能量隨時頻變化分布特征,實現了時頻同時局部化的目的。

經分析對比發現：傳統的FFT譜普遍存在著低頻時低估信號幅值并且高頻時又過度放大信號幅值的問題,本文所改進的方法能在一定程度上修正這種誤差。實驗結果表明：基于改進的希爾伯特-黃變換在地震強震動特征提取過程中具有顯著優點,與前人利用EEMD分析地震加速度記錄相比,抑制模態混疊現象效果更為突出,其得到的邊際譜和時頻譜可在最大程度上保留原始數據中的主要特性,可為類似破壞性淺源地震的強震動特征分析提供更有效的信息參數,更適于處理非平穩信號,為現代信號應用分析于強震動特征提供另一種新思路。