進氣壓力畸變對某渦軸發動機影響分析研究

楊宇飛 王召廣 黃 興 屠寶鋒

（1.中國航發湖南動力機械研究所，湖南株洲 412002；2.南京航空航天大學 能源與動力學院，江蘇南京 210016）

發動機氣動穩定性是考核發動機的一個關鍵指標，其直接影響了飛機的使用和任務能力[1]。進氣壓力畸變是影響發動機穩定工作的最主要因素之一[2]。目前，國內關于進氣壓力畸變方面的研究主要集中在渦扇發動機[3-5]，針對渦軸發動機進氣畸變的研究還比較少，而且渦軸發動機在進氣畸變方面與渦噴、渦扇發動機也存在一定差異[6-7]。

本文基于經典平行壓氣機理論，引入周向摻混系數來考慮不同扇區間質量、動量和能量的交換；通過求解積分形式的、帶源項的二維非定常歐拉方程，計算發動機內部的流動參數，再結合適當的穩定性判據，判斷發動機在給定的進氣畸變條件下是否發生氣動失穩[8]。

1.計算模型

1.1 物理模型

本文針對某型渦軸發動機開展研究，根據對象的幾何特點以及工程經驗，建立圓柱坐標系計算域和網格。坐標系包括:周向、軸向和徑向。但是大量研究已經表明徑向畸變對發動機穩定性的影響比周向畸變小，可以忽略不計。因此，三維坐標簡化為二維坐標系，模型簡化及軸向單元劃分如圖1 和圖2 所示。

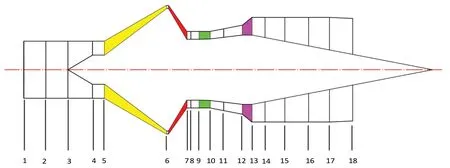
圖1 軸流-離心式渦軸發動機簡化模型

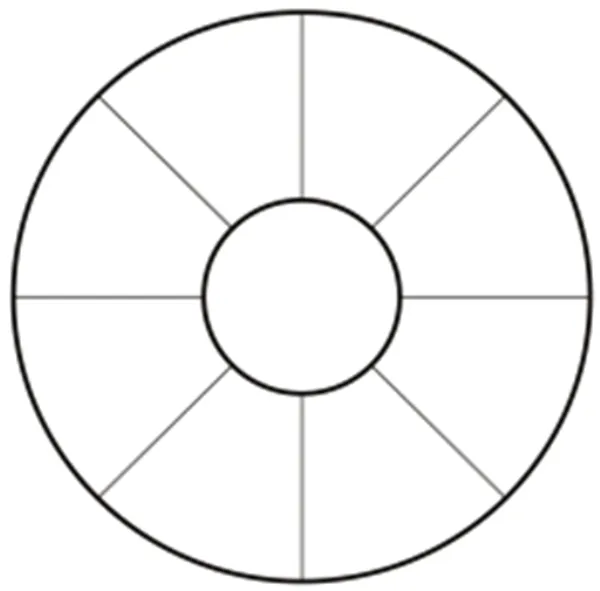
圖2 周向計算單元

周向和軸向的控制單元將計算域劃分為一系列單獨計算單元，同時選擇部件之間的交界面，建立整機的計算網格。周向上，將發動機沿周向等分成多個扇形塊，并假定每個扇形塊中的部件具有與完整部件相同的特性，相鄰的軸向站和周向站之間構成一個控制體。

1.2 數學模型及求解方法

針對計算域中的每一個控制體，采用二維歐拉方程描述控制體內部的流動：

其中，g表示壓氣機或其他部件的引氣或注氣量，規定引氣時g取負號，注氣時取正號；下角標g表示引氣或注氣參數，θ表示周向分量。

直接對上述方程求解是十分困難的，為了滿足本文提出的計算功能，引入了假設條件，對上式進行簡化。引入向量=(,vθ,T,P)，上式可以寫成：

此時，只要給定進口邊界條件和初值，可以通過求解式（2）得到發動機相關截面參數和性能特性。

1.3 進口邊界

本模型的采用綜合壓力畸變指數描述進口總壓畸變，進口總壓畸變條件包含有序的畸變和隨機的動態畸變：

有序周向壓力畸變P0＊(θ,t)又包括穩態壓力畸變和非定常壓力畸變兩部分：

其中，P＊(θ)為穩態壓力畸變。使用穩態壓力畸變指數?0來表示穩態壓力畸變的強度，其表達式如下：

dP＊/dt(t-t0)為非定常壓力畸變，隨時間變化作用在整個進口截面上，可用來描述沖擊波這一類階躍式的總壓等熵擾動。這種擾動對于渦軸發動機一般不會遇到，本文不予考慮。

動態總壓畸變也可以稱為面平均紊流度，表示總壓脈動的定量特征，即總壓空間不均勻度隨時間迅速變化。其定義式如下：

本文采用由穩態畸變指數?0和動態總壓畸變指數εav相疊加的綜合畸變指數W來描述綜合總壓畸變強度。當采用插板產生總壓畸變時，總壓畸變中含有穩態分量和動態分量。從試驗數據看，兩種分量的比值一般在0.4～0.6。因此總壓畸變其表達式為：

1.4 失穩準則

壓氣機計算結果中出現負的軸向速度，則認為發動機超出喘振線工作，此時壓氣機失穩。

2.模型驗證

渦軸發動機國軍標通用規范中采用DC60 指數形式描述進氣壓力畸變，即假設發動機進口周向存在60°的低壓區，計算公式如下：

其中，Pt,av,60表示發動機進口截面上、最低壓力區60°扇形范圍內的面平均總壓；Pt,av表示發動機進口截面上的平均總壓；0.5ρv2表示發動機進口截面上平均動壓頭，與來流的密度和速度有關。

試驗中進氣畸變模擬采用插板法[9-10]，獲得DC60 指數。為對比計算和試驗數據，必須將DC60 指數轉換為周向不均勻度，然后假設動態壓力畸變分量為零，再得到綜合壓力畸變指數。

在畸變試驗過程中，環境總溫301.3K，環境壓力100500Pa，發動機處于中間狀態，DC60=-0.4055。轉換成綜合壓力畸變指數W=0.5346%。

表1 給出均勻進氣下本模型和試驗情況的對比，表2 給出了渦軸發動機中間狀態在綜合壓力畸變指數等于0.5346%情況下的計算和試驗結果。

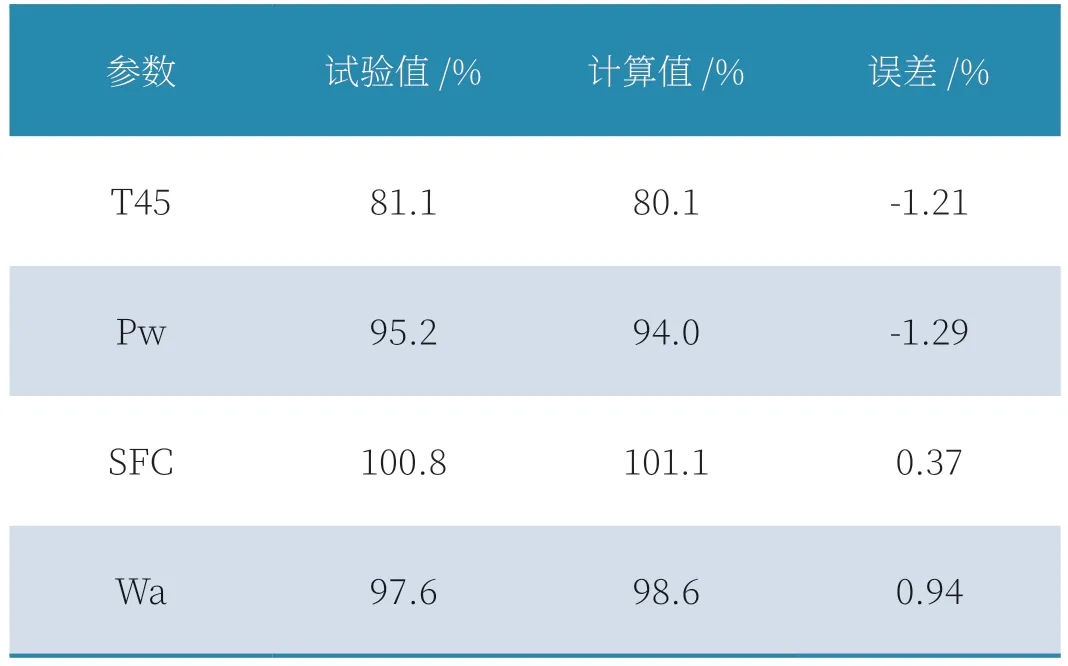
表1 中間狀態均勻進氣情況下試驗和計算結果對比

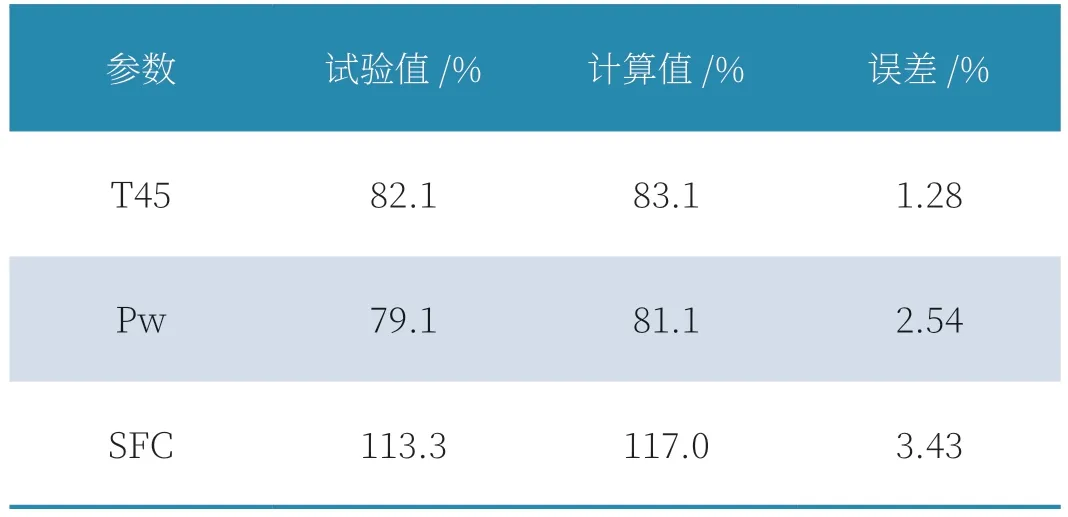
表2 中間狀態W=0.5346%，試驗和計算結果對比

可以看出在下本模型計算數據與試驗值基本吻合，表明本模型的可以在一定程度上反映發動機真實畸變下的性能狀態。

3.壓力畸變對性能影響

3.1 對穩定性的影響

該渦軸發動機主要由軸流加離心式壓氣機、回流燃燒室、軸流燃氣渦輪和動力渦輪組成。其正常工作線如圖3所示。

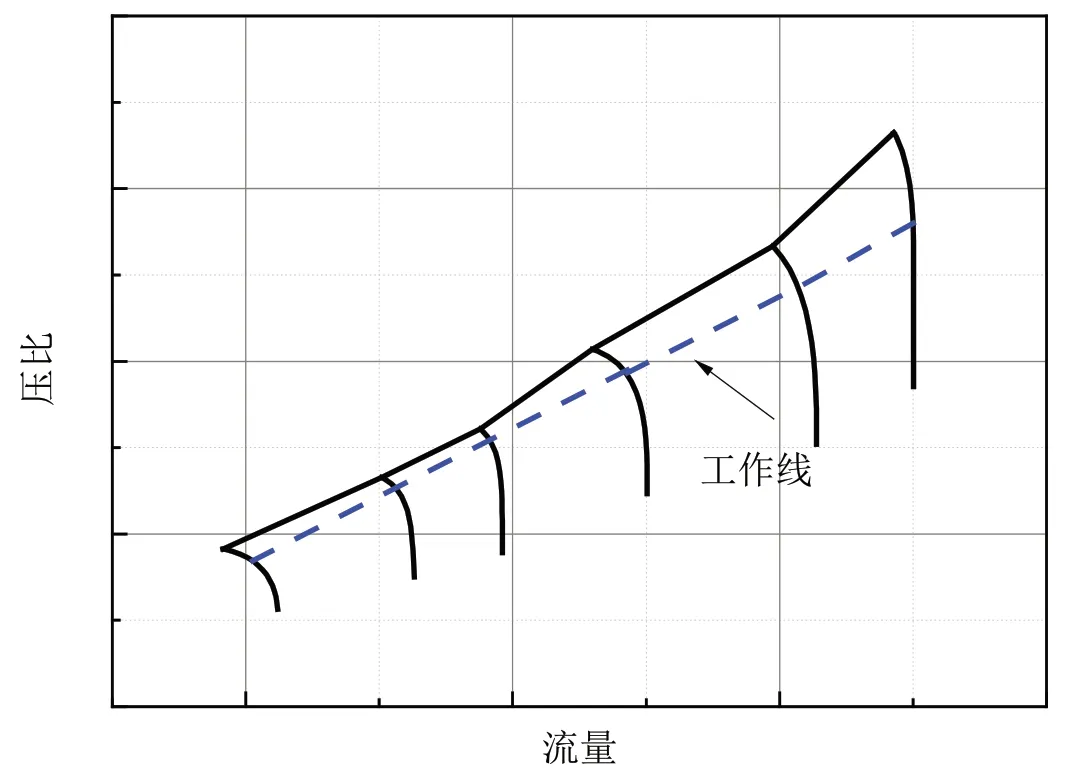
圖3 發動機工作線

表3 給出了不同轉速情況下的臨界壓力畸變指數和壓力畸變敏感系數，隨著轉速降低，發動機原始可用穩定裕度逐漸減小、臨界綜合壓力畸變指數也逐漸降低，壓力畸變敏感系數逐漸增大，表明該發動機抗壓力畸變能力逐漸變弱。

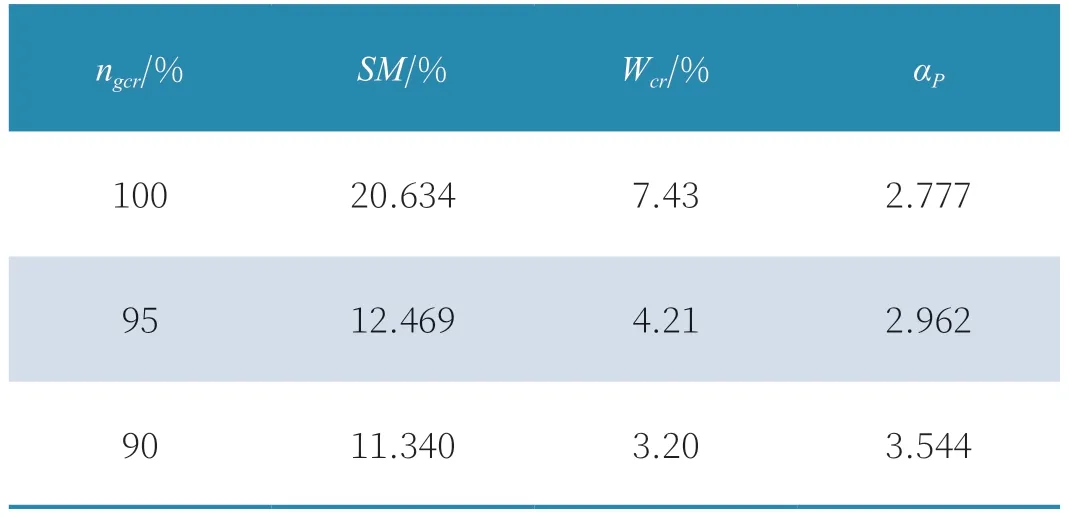
表3 不同轉速下臨界壓力畸變指數和敏感系數

根據經驗，發動機抗壓力畸變能力大小與壓氣機特性線的陡峭程度有關，從圖3 的組合壓氣機特性圖就可以看出，隨著轉速降低，工作線斜率絕對值逐漸降低，陡峭程度變小，特性線越來越平緩，導致發動機抗壓力畸變能力下降。因此在設計時，為提高發動機抗壓力畸變的能力，需要盡可能提高共同工作點在等轉速線上的斜率。

圖4 給出了100%設計轉速，在綜合壓力畸變指數等于5%時，穩態壓力畸變指數沿軸向的傳遞過程。可以看出，壓力畸變在壓氣機內傳播時，快速下降。但流過軸流級出口后，在離心壓氣機又出現了回彈。經過離心壓氣機以后，壓力畸變快速衰減，出口的壓力畸變指數是進口的0.38 倍，衰減了62.08%。計算結果表明，該渦軸發動機進氣畸變易發生在第一級軸流壓氣機以及離心壓氣機。

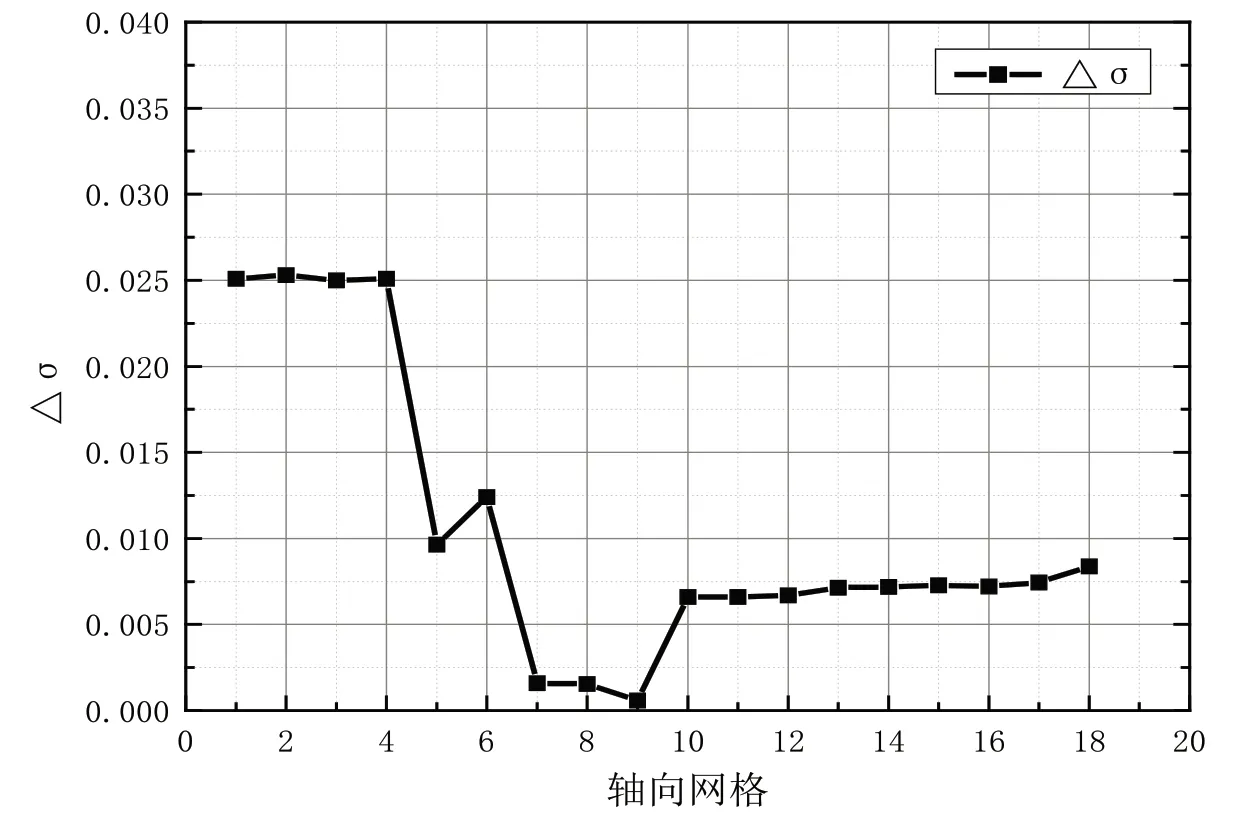
圖4 穩態壓力畸變指數的軸向傳遞

為驗證發動機綜合畸變指數隨時間增長，發動機的工作情況。圖5～圖7 給出了100%設計轉速時，綜合壓力畸變指數等于2%、4%、10%時，各扇區工作點在時間推進計算過程中瞬時位置的變化。其中扇區1 是高壓區，扇區2 是低壓區。

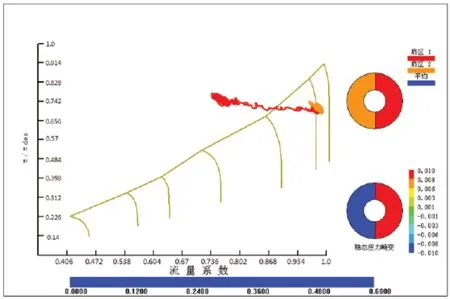
圖5 W=2%各扇區工作點

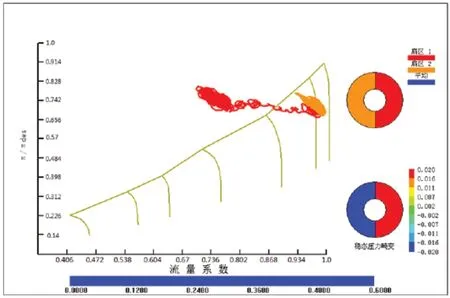
圖6 W=4%各扇區工作點

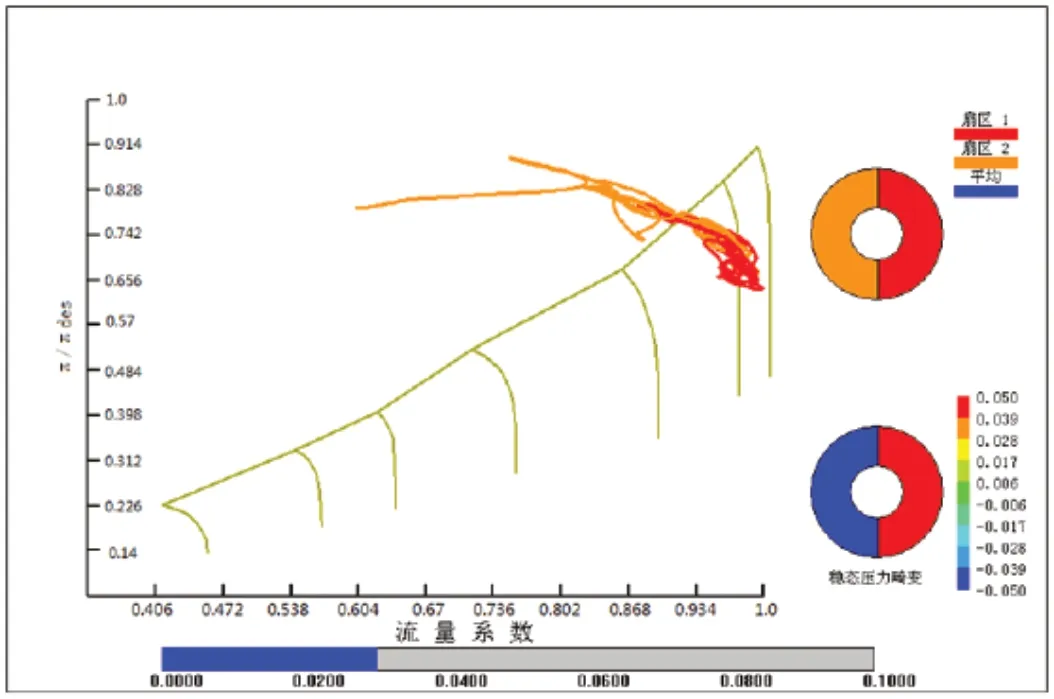
圖7 W=10%各扇區工作點

可以看出，扇區1 在時間推進的過程越過穩定邊界，但是最后又能夠穩定在穩定邊界左側某個位置，并沒有導致流量系數進一步降低，始終處于流量大于零的情況，因此發動機能夠穩定工作。當綜合壓力畸變指數等于4%時，發動機最終能夠穩定工作，但是，扇區1 和扇區2 工作點的脈動幅值比綜合壓力畸變指數1%要大。當綜合壓力畸變指數等于10%時，發動機兩個扇區的工作點無法穩定在某個位置，流量快速降低，最終出現負速度，發動機氣動失穩。

3.2 進氣壓力畸變對性能的影響

圖8 給出了畸變區周向范圍等于180 度時，100%設計轉速時綜合壓力畸變指數分別等于1%、2%、3%、4%、5%、6%和7%時發動機的軸功率和排氣溫度。可以看出，隨著綜合壓力畸變指數的不斷增加，發動機輸出的軸功率逐漸降低、排氣溫度逐漸提高。

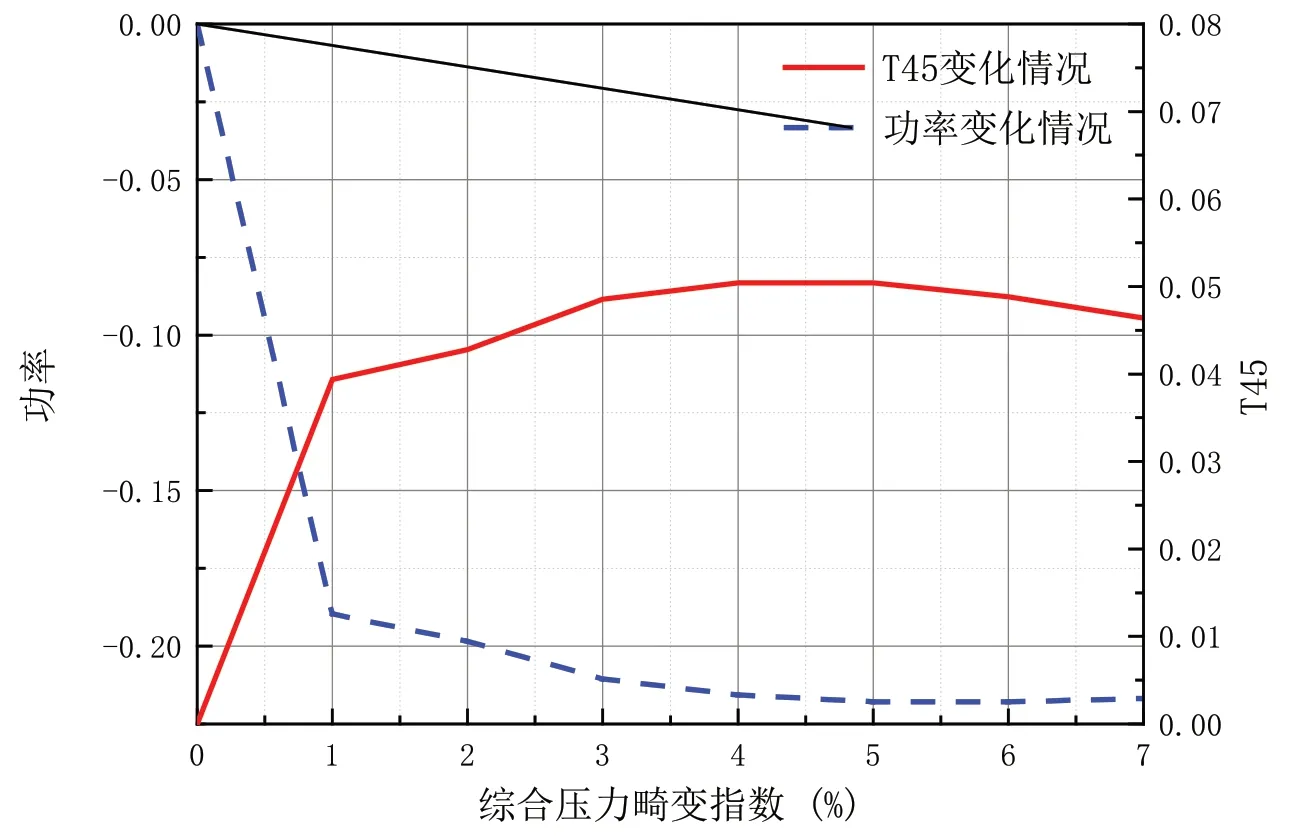
圖8 功率和T45隨綜合壓力畸變指數的變化

4.結論

本文詳細介紹了進口壓力畸變對軸流離心組合式的渦軸發動機氣動穩定性影響的計算方法，并對該渦軸發動機在典型進口壓力畸變作用下的穩定性和性能進行了計算，結果表明：

（1）由于該渦軸發動機最大狀態下壓氣機流量裕度小，導致轉速較低時的抗壓力畸變能力較弱。

（2）相同轉速和壓力畸變條件下，該發動機畸變發生位置易出現在第一級軸流壓氣機或離心壓氣機處。

（3）隨著綜合壓力畸變指數的不斷增加，發動機輸出的軸功率逐漸降低、排氣溫度逐漸提高。