基于機器學習算法的信用風險量化模型研究

李沐勛

摘要：傳統的信用風險計量模型難以處理高維數據和非線性問題，多具備較嚴格的假設條件，計算結果常與實際情形存在較大的誤差。本文綜合考慮影響信用風險的內生變量和外生變量，使用更優的非線性變換方式擬合數據，并借助機器學習強大的算力和學習迭代優勢量化信用風險。實證結果表明，該模型算法可提高預測結果的擬合度和準確性。

關鍵詞：債券市場；機器學習；信用風險計量

中圖分類號：F832.5? ? ? ? 文獻標識碼：A? ? ? ? 文章編號：1007-0753（2023）04-0075-09

一、引言

信用風險作為金融市場風險的重要組成之一，其被衡量的方式始終被市場參與方所重視。投資者、金融機構、監管部門出于風控需求，對信用風險衡量的要求也趨于更加精準和動態。信用風險計量模型則在其中扮演最為關鍵和重要的角色，其科學性和準確性成為風險計量結果好壞的基礎性因素。

金融學中大部分研究對象的本質都是復雜、多維和非線性的。傳統的信用風險計量模型難以處理高維數據和非線性問題，多具備較嚴格的假設條件，并且算力難以支持大量模擬和迭代優化，因此計算結果常與實際情形存在較大誤差。

隨著金融工程的發展和計算機算力的增長，機器學習作為人工智能的重要成果之一，在金融風控領域的應用日益廣泛。該類算法將概率論、統計學、最優化理論等科學理論與計算機的強大算力相結合，既可快速、自動地處理高維數據，還能在不斷學習和優化過程中提高模型的泛化能力，通過復雜多樣的函數輸出更準確的預測結果。可以預見，機器學習模型的應用和迭代將帶動信用風控技術進入新紀元。

本文利用統計學原理以及機器學習算法，構建資產信用風險溢價和違約概率量化模型，以解決傳統模型中的各類局限和不足，輸出更準確的量化預測結果。

二、傳統信用風險衡量模型

信用風險衡量模型的發展經歷了三個階段：第一階段為20世紀60年代之前的專家分析法，通過專家經驗和主觀分析來評估信用風險；第二階段為20世紀70年代至90年代的信用評分模型，包括線性概率模型、Logit/Probit模型和Z-score模型，20世紀60年代的信用卡業務催生了該類模型的發展，這也是數學模型首次應用于信用風險領域；第三階段為20世紀90年代至今的違約概率模型，例如KMV模型、CreditMetrics模型和CreditRist+模型，該階段的模型將金融理論與數學相結合，對信用風險的評估由分類上升至計量。目前，信用評分模型仍被國內外評級機構和多數金融機構應用于信用風險評估，違約概率模型則多被商業銀行使用，用于信貸審批、信用卡額度審批和信用風險敞口的計算。

然而信用風險衡量模型的發展已停滯近三十年，其固有的缺陷也日益暴露，難以滿足更高的風控需求。信用評分模型使用了較多的內生變量，例如財務數據、主體資質、資產特征等，但最終僅輸出分類結果，并無進一步的量化信息；并且模型計算中僅使用初等函數，應用的數學理論較為簡單。而違約概率模型雖然實現了進一步的風險計量，但考慮的內生變量較少，例如KMV模型中僅考慮資產與負債規模的內生變量，CreditMetrics模型和CreditRist+模型僅使用了違約頻率的外生變量，并且應用的統計學模型局限于正態分布，弱化了擬合度和尾部風險。此外，傳統模型中尚未探索出信用風險溢價與違約概率之間的映射關系，以及對違約的預警功能。

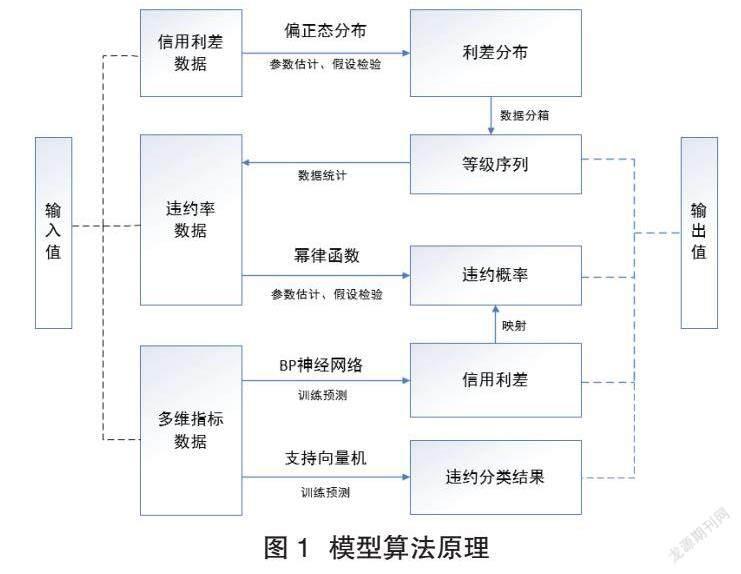
三、模型算法原理

外生變量是資產信用風險變化的直接體現，例如生存率、死亡率（違約率）、等級遷徙率等，可通過簡單的計算統計得到。內生變量是影響資產信用風險的本源性因素，例如資產歸屬主體的資質、財務狀況和經營狀況，它們之間通過復雜的聯系和變化影響著資產的違約概率，難以用簡單的函數進行表達。此時可通過引入具有代表性的標簽值作為中間變量，一方面構建更顯著的映射特征，另一方面強化深度，尋找更優的非線性變換方式以擬合數據。

鑒于此，在變量選擇上，本文使用財務、經營、行業和宏觀數據等與資產相關的特征值作為內生變量，多維度囊括關于資產的有效信息；使用標簽屬性顯著的信用利差作為中間變量，根據信用利差和違約頻率的正相關性，建立單變量映射函數；使用違約頻率作為外生變量，將模型訓練結果擬合至直觀的統計數據。通過上述變量的選擇，模擬信用風險由內至外的演變過程。

本文量化模型先后運用分布擬合、BP神經網絡和支持向量機等算法原理，輸入變量包括資產到期收益率、無風險利率、定性指標和定量指標等特征值以及違約頻率統計值；輸出變量包括信用利差、等級序列、違約概率和違約分類結果。

四、模型算法的實證

（一）信用利差與偏正態分布

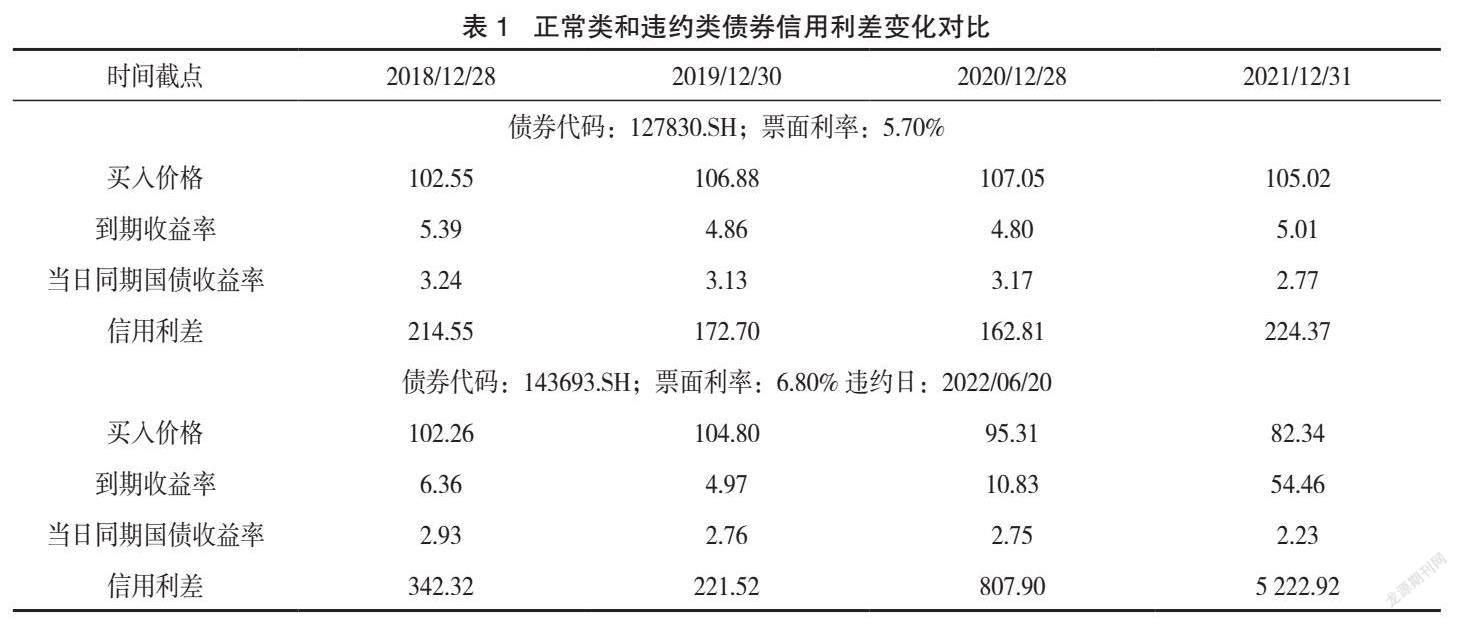
信用利差即信用風險溢價，金融市場體現風險與收益對等的原則，越低的信用利差說明資產的違約風險越小。對信用債而言，業界多采用票面利率與國債收益率之差作為信用利差，由于票面利率多為固定利率，信用利差的變化也單純由國債收益率的變動引起。本文選擇債券到期收益率代替票面利率，到期收益率的變動可體現資產回報率的變化，便于動態反映信用風險。當投資者認為債券發行人信用質量顯著下降時，該只債券遭到拋售，買入價格的下降和剩余期限的減少導致到期收益率上升，信用利差隨之上升，如表1所示。而到期收益率的上升變相地增加了發行人的還款壓力，增大了債券的違約概率。

目前業界對信用利差數據的建模多采用正態分布，但正態分布具有左右完美對稱的性質，而實際情形中利差分布較多呈現左偏或右偏、單側瘦尾或肥尾的狀態，此情形下，使用正態分布建模常導致某個區間的累積分布值被高估或低估，模型誤差增大。例如默頓、KMV和CreditMetrics等模型中正態分布的應用均導致了模型結果與數據實際呈現的肥尾現象不符。因此，本文引入偏正態分布對利差數據進行建模，保證模型具備更高的擬合度和精準度。

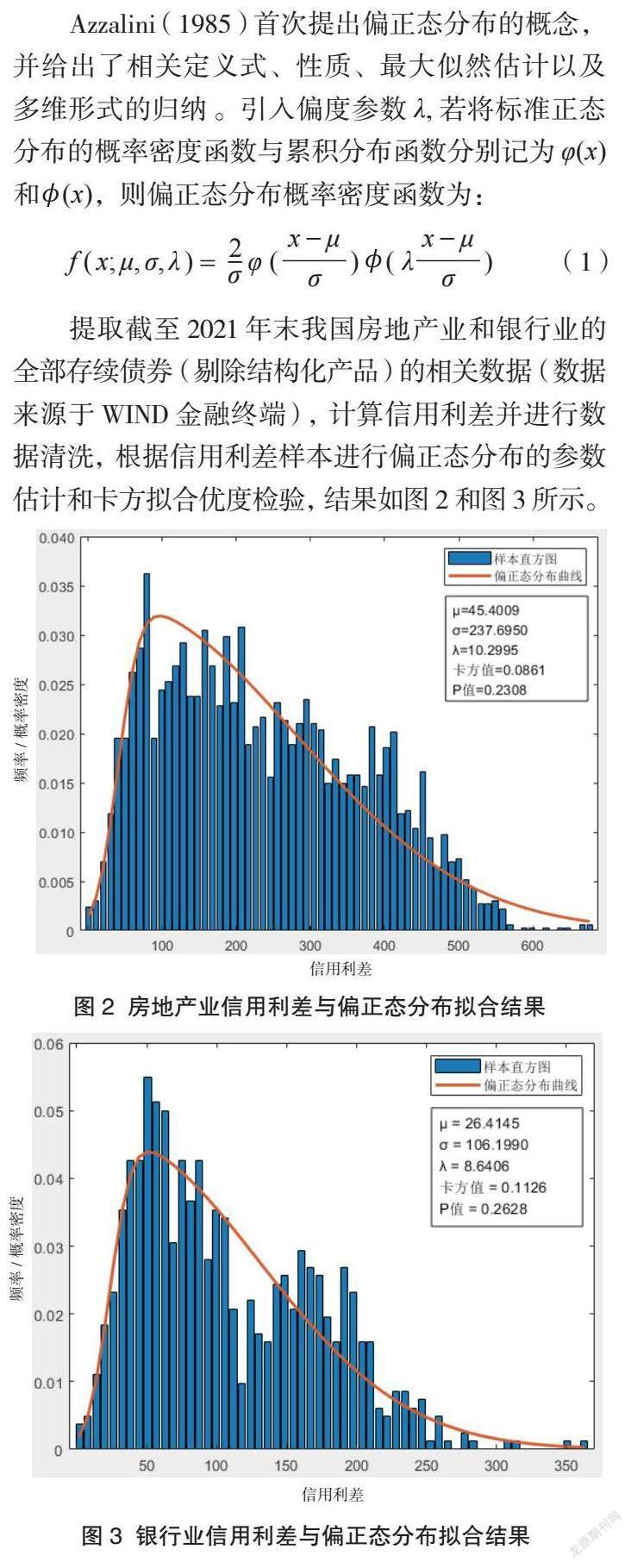
Azzalini（1985）首次提出偏正態分布的概念，并給出了相關定義式、性質、最大似然估計以及多維形式的歸納 。引入偏度參數λ，若將標準正態分布的概率密度函數與累積分布函數分別記為φ（x）和（x），則偏正態分布概率密度函數為：

f （ x; μ， σ， λ ） =? 2-σ φ （? ）（ λ ）? ? ? ? ?（1）

提取截至2021年末我國房地產業和銀行業的全部存續債券（剔除結構化產品）的相關數據（數據來源于WIND金融終端），計算信用利差并進行數據清洗，根據信用利差樣本進行偏正態分布的參數估計和卡方擬合優度檢驗，結果如圖2和圖3所示。房地產業和銀行業樣本容量分別為3 282個和835個，P值分別為0.230 8和0.262 8，結果均無顯著性差異，模型結果和實際數據具備一致性。可視化效果同樣說明，概率分布與原始數據擬合度較高，偏正態分布可更準確地反映信用利差分布的實際情況。

對信用利差進行分箱處理，建立信用等級和信用風險的映射關系，利差數值越小代表信用風險越低，對應的信用等級越高。此處分箱處理的為理論利差分布，而非樣本觀測值。

常用的無監督學習數據分箱方法包括等距分箱、等頻分箱和聚類分箱等。聚類分箱法由于對特征值定義缺乏明確的量化標準，類個數取決于建模人員的主觀意見（例如將債券分為投資級和高收益級），因此不作為備選方法。等距分箱法是對隨機變量進行等距分組，會產生樣本數量較高（眾數）或極少（尾部）的箱體，對樣本數量較高的箱體的風控效果較差。從信用風險衡量的實際業務需求角度來講，分箱后建立的等級序列需具備較好的區分效果，以便嚴格把控風險和降低投資虧損概率。提升序列區分度問題存在最優解，即等級序列與概率之間呈均勻分布，此時不存在任何一個箱體的區分度高于或低于其他箱體，因此選擇等頻分箱法更符合建模需求。

以箱體數量9個為例，分別代表1—9個信用利差區間即等級序列。每個箱體在偏正態分布上具有相等的積分值，因此通過逆累積分布函數即可求得每個箱體的利差區間閾值。為方便理解，同樣給予級別符號對應表示。表2為房地產業樣本的等頻分箱結果。可以看見，測試樣本的分箱結果與理論值較為接近，卡方擬合優度檢驗結果無顯著性差異，整體區分度較顯著。

（二）違約概率與冪律分布

對違約數據的統計表明，當資產的信用質量下降時，違約概率將以類指數形式增長。目前我國較多商業銀行使用指數分布對違約概率進行預測（周四軍和彭建剛，2008），即首先根據卡普蘭生存分析法統計不同時間期限下樣本的累積違約頻率，再根據數據真值進行指數分布擬合得到對違約概率的預測。但指數分布的無記憶性特點與違約事件相矛盾，表現為系統內下一時刻的狀態僅與當前狀態有關，而與過去無關，該特點忽略了信用質量變化過程對違約概率所造成的影響，因此其盡管與違約率數據擬合度較高，但并不具備經濟學解釋性。

冪律分布同樣體現出與違約率數據的高擬合度，并且其內在原理應用于違約事件具備良好的解釋性。冪律現象可簡單描述為事件發生的概率與事件規模的某個負指數成比例。導致冪律現象的原因包括自組織臨界論、優先鏈接理論和大偏差理論，各理論均在極端事件的金融問題的應用中有著重要作用（胡海波和王林，2005）。

將等級序列定義為隨機變量x，對應的y值為違約概率。在樣本數據同時包括x值和y值時，使用曲線擬合可獲得目標函數表達式和擬合優度，實現參數估計和假設檢驗的效果。本文以穆迪評級官方披露的1983—2020年全球平均累積違約率數據為樣本進行檢驗，各期限下的違約數據擬合效果如表3所示，10年期樣本的擬合結果如圖4所示。

根據表2信用利差的等頻分箱數據，統計序列1—9下房地產業樣本1年期違約率，使用冪律分布進行曲線擬合，結果如表4所示。由于我國信用債市場目前所積累的違約樣本依舊較少，樣本數據存在刪失和截尾現象，因此擬合效果有所減弱。

（三）信用利差與違約概率

根據前述原理，可建立信用利差與違約概率之間的函數關系，步驟如下：

（1）定義資產的信用利差為x，信用風險為u，違約概率為y，均為連續變量；

（2）信用利差x取值范圍為[0，+ ∞）；

（3）信用風險u取值范圍為[0， k]，k越大代表信用風險越大；

（4）違約概率y取值范圍為[0， 1]，理論上可取至1；

（5）信用利差x服從偏正態概率分布，定義偏正態概率分布的累積分布函數為skew （x）；

（6）等頻分箱原則表明信用風險u的大小通過信用利差x在偏正態分布中所處的位置體現，x的累積分布函數值越小則信用風險越低，skew（x） 與u之間為線性正相關，滿足：

u = k ·skew（x）? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（3）

（7）給定期限下，信用風險u和違約概率y之間滿足參數為C和α的冪律函數：

y = C · u-α? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （4）

（8）則信用利差x與違約概率y之間的函數關系為：

y = C · k-α[skew（x）]-α? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （5）

將前述偏正態分布和冪律函數的參數估計值代入公式（5），在利差樣本最小值和最大值范圍內創建等差序列，生成利差向量x，并繪制函數曲線。圖5為理論模型下房地產業信用利差與1年期違約概率的映射關系。樣本中信用利差最大值為686.29bp，此時資產的1年期違約概率約為11.96%。

（四）信用利差預測與BP神經網絡

計算機算力的增長和人工智能的發展推動了機器學習在金融風控領域的應用。其中，神經網絡算法（聞新等，2015）具有優良的多維非線性映射能力和柔性的網絡結構，其理論上可擬合出變量任何形式的變化，因此在機器學習算法中具備極高的上限。其中，由Rumelhart和Mcclelland（1986）提出的BP神經網絡是基于誤差逆向傳播（Back Propagation，BP）對多層前饋神經網絡進行訓練的算法。該算法并非在建模前將描述變量之間關系的函數表達式揭露并固定下來，而是使用最速下降法，通過反向傳播方式反復訓練和調整網絡的權值和偏差，使輸出結果與期望結果盡可能地接近，即網絡輸出層的誤差平方和最小。

本文首先選擇截至2021年末房地產業和銀行業存續債券的發行主體，作為兩組樣本進行對比和模型穩健性檢驗；其次選擇結構化財務數據作為特征值，先后使用信用利差和等級序列作為標簽值，進行BP神經網絡訓練。數據清洗方面，對相同發行人的債券僅保留單一值，并剔除信用利差小于零的樣本。特征值選擇方面，選擇WIND金融終端中包括盈利能力、收益質量、現金流量、資本結構、償債能力和運營能力的全部財務指標，分類進行主成分分析。選擇每類中主成分累積貢獻度大于90%的指標納入特征值，進行數據降維；同時對數據進行歸一化處理，消除不同特征值之間的量綱差距。最終房地產業樣本組的樣本數量為695個，特征值數量為23個；銀行業樣本組的樣本數量為820個，特征值數量為18個①。

需要指出的是，對信用利差的預測并不具備建立時間序列模型的條件。信用債發行主體的財務數據所披露的頻率通常以年度為基準，季度和半年度報告的數據完整性較差且未經過審計，數據集質量并不理想。而債券發行期限通常以3至10年為主，這意味著數據集的最大時間窗口通常在10個步長以內，若再對數據集進行訓練集與測試集的分割，則每個數據集的時間步長極短，模型難以在訓練學習中發現規律。因此，在對信用風險的動態監測過程中，應定期抓取存續樣本和采集特征值，重新訓練模型并獲得預測結果。

本文使用列文伯格·馬夸爾特算法，將訓練集、驗證集與測試集數量設置為2∶1∶1；隱含層數量根據經驗公式設置為? 層，其中n和m分別為輸入節點數量和輸出節點數量；經歷10輪完整學習，并記錄測試集回歸系數R的均值和最大值。

將僅使用財務指標的訓練過程記為“訓練1”，其測試集回歸結果如表5所示，可見訓練結果較為一般。銀行業的回歸系數高于房地產業，對信用利差預測的準確性高于對等級序列預測。在特征值中引入部分經營數據和文本數據以優化預測結果，對于房地產業樣本，在特征值中引入所在省份的GDP總量、GDP增速、股東背景和債券擔保方式；對于銀行業樣本，引入存貸款總額、不良貸款率、撥備率、凈息差和股東背景，并再次訓練記為“訓練2”。

訓練2測試集回歸結果如表6所示。可以看出，引入除財務數據外的其他評價要素后，模型預測的準確性顯著上升，其中房地產業的提升效果更為明顯。銀行業的回歸結果依然優于房地產業，可能與商業銀行所披露的數據質量更高、信用利差跨度較小有關。使用等級序列進行預測的準確性略低，可能與位于序列端點的樣本被誤分類有關。其中，銀行業在訓練2中回歸系數最高的一次學習結果如圖6所示。

信用風險的內源性體現出非結構化數據對風險衡量的重要性，即決定信用風險的因素不僅包括定量數據，還包括對定性指標的加工處理。由于定性指標判別所需的時長較長、工作量極大，本文僅進行了少量定性指標的判別，因此呈現的訓練結果并非最優，但仍優于傳統的信用風險衡量模型，特別是對評級結果95%以上集中于AA-以上的中國債券市場而言，可起到深度量化的效果。將新樣本的特征值數據輸入BP神經網絡模型，即可輸出該樣本信用利差的預測結果；再將輸出的信用利差代入公式（5），即可獲得對應時間期限下的違約概率。實際操作過程中，提取聚類后樣本在不同時間截點的信用利差、特征值數據和累積違約概率，即可通過BP神經網絡算法實現對信用風險的動態量化。

（五）違約預測與支持向量機

目前宏觀經濟下行導致信用風險加劇，資產違約問題日漸凸顯，金融風控對違約預警提出了更強的需求。支持向量機（SVM）為有監督學習中的廣義線性分類器，十分適合解決二分類和回歸問題（周志華，2016）。該算法根據VC維理論和結構風險最小原理，在樣本中求解最大邊距超平面，尋找分割樣本的最優決策邊界（Vapnik和Chervonenkis，1964） 。對于線性不可分問題，SVM通過徑向基函數核，將非線性低維空間樣本映射至高維空間，使其變為線性可分問題，在該空間中尋找最優分類超平面。因此，滿足利用高維財務數據解決二分類問題的違約預警需求（張杰和趙峰，2013）。

由于季度財務數據可獲取性較低，本文統一選取年度財務數據納入多維數據集。行業聚類上選擇房地產業樣本，該行業違約樣本較多，可降低樣本不均衡的影響。對于違約樣本，本文選取違約前的年度財務數據；對于未違約樣本，本文選取2021年末財務數據，代表存續債券發行人的最新財務狀況。在進行數據清洗、歸一化處理和主成分分析后，最終總樣本數量為585個，數據集特征值數量為30個；違約樣本數量為25個，未違約樣本數量為560個②。

違約事件的特點導致樣本顯著不均衡，因此使用誤分類代價增強和Stratified K-fold交叉驗證解決樣本不均衡和過擬合問題，增強訓練模型的穩定性。

誤分類代價增強方面，由于金融風控領域更注重對正樣本（即違約樣本）的篩選能力，以盡可能減小遺漏正樣本造成的損失，對誤分類正樣本的代價進行設置。權重設置為向上取整后樣本集中負樣本與正樣本數量的比值。

Stratified K-fold交叉驗證方面，將數據集分為5個容量相等的折疊，每個折疊具有相等數量的違約樣本；每次選取1個折疊作為測試集，剩余4個作為訓練集，并取訓練集中1個折疊為驗證集，重復5次直至每個折疊均用作驗證集，最終取驗證數據的平均精度作為結果。

本文使用一對一多類方式，分別使用以下核函數進行模型訓練。除優化高斯核之外，均對樣本數據進行標準化處理。最終測試集測試結果如表7所示，模型誤差如圖7所示。查全率反映實際違約樣本中預測正確的比例，因此在信用風險衡量方面，該指標相對查準率更被看重。綜合而言，高斯核和優化高斯核的SVM模型表現最優。優化高斯核模型為可優化模型中的最佳點超參數模型，對高斯核模型中的核尺度和框約束級別均做了調整，未對數據進行標準化處理。由于原始數據集指標中絕大多數為比率指標，其余規模指標在爬取時對計算單位進行了處理，因此模型表現未受到顯著影響。

結果反映出SVM算法的測試效果較好，可對違約風險進行有效預警。在資產存續期內，利用資產最近一期的財務數據建立多維數據集，可實現對違約風險的定期動態跟蹤，為投資決策的調整提供參考依據。

五、結論

（一）改進與創新

與傳統模型相比，本文一方面綜合考慮內生變量與外生變量，通過引入中間變量完整了信用風險傳遞的邏輯關系；另一方面，驗證了機器學習模型在信用風險衡量領域應用的可行性，依靠算力模擬和迭代優化，機器學習提高了量化結果的準確度。

在函數使用方面，本文模型弱化了線性和基礎函數在信用風險衡量領域的應用，使用非線性和積分變換等復雜函數映射變量關系，依靠BP神經網絡的多層網絡結構，實現更復雜更精細的算法。

在實際風控需求方面，等頻分箱處理、信用利差與違約概率映射、神經網絡隱含層數設置、特征值選擇和優化方向等內容均能對風控工作起到借鑒作用。

（二）局限性

外生變量的推論統計需要具備大量樣本，以避免欠擬合現象。因此，當資產為信貸資產時，商業銀行可通過積累的大量樣本進行數據擬合；而當資產為標準化債券時，由于我國債券市場積累的違約樣本不足，刪失和截尾現象較多，數據擬合度難以提升。

在BP神經網絡訓練方面，受限于人力成本和時間成本，本文未將獲取較為困難的經營數據和非結構化數據納入數據集，因此測試結果并非最優。未來，在特征值中加入處理后的文本和字段信息，可進一步提升模型泛化能力。

各類機器學習均具備一定局限性。例如BP神經網絡易出現收斂速度慢和局部極小值的問題；支持向量機對缺失數據和異常數據較為敏感，對數據預處理要求較高。同時多數機器學習具有“黑箱特性”，即算法過程難以使用人類語言描述，困于被廣泛理解和接受。

（三）政策建議

本文構建的模型可幫助投資者或風控人員量化信用風險和預警違約風險，使其根據自身需求進行資產配置或調整投資頭寸，做到風險和收益的平衡。對監管機構而言，有助于其把控市場整體信用風險，為監管政策的制定提供借鑒，落實經濟回穩向上的發展政策。因此，對金融市場的信用風險防控，本文提出以下建議：

一是加強信息披露維度和頻率，推進數據基礎設施建設。數據基礎設施的完善可提升風險量化的精準性和風險監測的及時性，而目前交易市場中關于各類資產的違約率數據存在刪失和截尾現象，披露頻率較低，影響信用風險衡量的準確性和動態跟蹤。對此，應加強公開市場數據披露的維度和頻率，提升數據的有效性和時效性。

二是規范信息披露口徑和標準。商業銀行受到嚴格監管，所披露的規范化數據提升了數據集質量，有利于降低金融市場中的信噪比，提高模型的訓練效果。相比而言，其他行業的數據口徑不一、可使用指標數量較少，增加了噪聲信息。對此，各類非金融企業行業協會應規范數據披露標準，包括統計準則、口徑和管理方法等，提升數據質量和真實性。

三是加強高風險資產市場化經營能力，健全違約資產處置機制。借鑒成熟的金融市場的機制設置經驗，例如完善高收益債券市場和違約資產的分類處置，真實反映信用風險，進而提升高風險資產的定價合理性、交易流動性和市場穩定性，實現整個金融市場的資源配置優化、風險分散和經濟調節等功能。

注釋：

① 數據集較為龐大，限于篇幅本文不再列出，僅作者留存備查。

② 限于篇幅本文不再將數據集列出，作者留存備案。

參考文獻：

[1] AZZALINI A. A class of distributions which includes the normal ones[J]. Scandinavian Journal of Statistics， 1985，12：171-178．

[2] 周四軍，彭建剛.商業銀行信用風險量化新方法：死亡率模型[J].統計與決策， 2008（14）：26-28．

[3] 胡海波，王林.冪律分布研究簡史[J].物理， 2005， 34（12）：889-896．

[4] 聞新，李新，張興旺．應用MATLAB實現神經網絡[M].北京：國防工業出版社， 2015：95-159．

[5] RUMELHART D E， MCCLELLAND J L.Parallel Distributed Processing[M]. Massachusetts： MIT Press， 1986：318-362.

[6] 周志華.機器學習[M].北京：清華大學出版社，2016：? 125-135．

[7] VAPNIK V，CHERVONENKIS A. A note on class of perceptron[J]. Automation and Remote Control， 1964， 25（01）.

[8] 張杰，趙峰.基于支持向量機的中小企業技術信貸違約預測[J].統計與決策， 2013（20）：66-69．

（責任編輯：張艷妮/校對：唐詩柔）

Abstract： Traditional credit-risk measurement models have difficulty in dealing with high-dimensional data and nonlinear problems， and often have strict assumptions， leading to large errors between the calculated results and the actual situation. This paper considers both endogenous and exogenous variables that affect credit risk， uses a more optimal nonlinear transformation method to fit the data， and quantifies credit risk with the powerful computational and iterative learning advantages of machine learning. Empirical results show that the algorithm of this model can improve the fitting and accuracy of predictive results.

Keywords： Bond market; Machine learning; Credit-risk measurement