不確定平方和凸多項(xiàng)式優(yōu)化的SDP松弛與魯棒鞍點(diǎn)刻畫

譚 玟,孫祥凱

(重慶工商大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,重慶 400067)

凸多項(xiàng)式優(yōu)化是凸優(yōu)化問題的一個(gè)重要模型,在自動(dòng)控制系統(tǒng)、交通運(yùn)輸和工程設(shè)計(jì)等領(lǐng)域應(yīng)用廣泛,并取得了很多研究成果[1-4].平方和凸多項(xiàng)式優(yōu)化作為凸多項(xiàng)式優(yōu)化問題的一個(gè)子類,近年來也得到廣泛關(guān)注,因?yàn)樗梢缘葍r(jià)地表示為一個(gè)半定線性優(yōu)化問題,并能通過內(nèi)點(diǎn)法有效解決[5].此外,平方和凸多項(xiàng)式優(yōu)化具有精確的半正定規(guī)劃(SDP)松弛問題,且原問題與其對偶問題之間存在零對偶間隙[6-8].

上述研究平方和凸多項(xiàng)式優(yōu)化問題時(shí),通常需要假設(shè)所考慮優(yōu)化問題模型的數(shù)據(jù)是精確的.但在實(shí)際應(yīng)用中,由于測量、制作誤差以及不精確數(shù)據(jù)等諸多因素影響,所建模型的優(yōu)化問題不可避免地存在不確定數(shù)據(jù).因此,帶有不確定參數(shù)的平方和凸多項(xiàng)式優(yōu)化問題目前已引起人們廣泛關(guān)注.例如: Jeyakumar等[9]基于常見的不確定集,得到了不確定平方和凸優(yōu)化問題的魯棒解刻畫和精確的SDP松弛問題; Chuong[10]借助線性矩陣不等式以及平方和條件,研究了不確定多目標(biāo)平方和凸多項(xiàng)式優(yōu)化問題的最優(yōu)性條件和對偶定理; Jiao等[11]借助標(biāo)量化方法,刻畫了不確定多目標(biāo)平方和凸多項(xiàng)式優(yōu)化問題的魯棒有效解,并證明了對應(yīng)的標(biāo)量問題與松弛問題之間的零對偶間隙; Chuong等[12]借助一類魯棒型閉凸錐約束規(guī)格,刻畫了不確定凸二次多目標(biāo)優(yōu)化問題的魯棒(弱)有效解的最優(yōu)性條件.

受上述研究結(jié)果的啟發(fā),本文給出一類不確定平方和凸優(yōu)化問題的魯棒鞍點(diǎn)定理.首先,借助魯棒優(yōu)化方法,引入不確定平方和凸多項(xiàng)式優(yōu)化問題的魯棒對等問題; 然后,借助一類魯棒型特征錐約束規(guī)格,得到該不確定平方和凸多項(xiàng)式優(yōu)化問題的精確SDP松弛問題; 最后,引入該不確定平方和凸多項(xiàng)式優(yōu)化問題的Langrange函數(shù),并借助平方和條件給出其魯棒鞍點(diǎn)定理.

1 預(yù)備知識

定義1[5]設(shè)f為n上的實(shí)多項(xiàng)式,若多項(xiàng)式

f(x)-f(y)-f(y)T(x-y)

注1顯然,平方和凸多項(xiàng)式是凸多項(xiàng)式,但反之不一定成立[13-14].進(jìn)一步,凸二次函數(shù)和凸可分離多項(xiàng)式都是平方和凸多項(xiàng)式.此外,一個(gè)平方和凸多項(xiàng)式可能既不是二次的也不是可分離的[5].

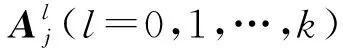
本文考慮如下不確定平方和凸多項(xiàng)式優(yōu)化問題(UP):

其中vj(j=1,2,…,m)為不確定參數(shù)且屬于不確定集Vj?k,f:n→和gf:n×Vj→(j=1,2,…,m)均為給定的函數(shù).若無特殊說明,本文總假設(shè)f是平方和凸多項(xiàng)式,對任意的vj∈Vj,gj(·,vj)是平方和凸多項(xiàng)式,對任意的x∈n,gj(x,·)是仿射函數(shù),即

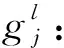
定義2問題(UP)的魯棒可行集定義為

F∶={x∈n|gj(x,vj)≤0,?vj∈Vj,j=1,2,…,m}.

2 精確SDP松弛

下面借助一類魯棒型約束規(guī)格,建立問題(UP)的精確SDP松弛問題.

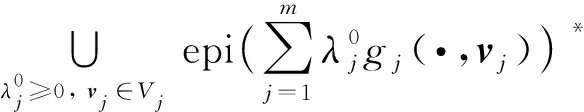
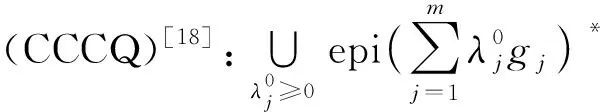
2) 顯然,若魯棒Slater條件

{x∈n|gj(x,vj)<0,?vj∈Vj,j=1,2,…,m}≠?

成立,則魯棒型特征錐約束規(guī)格(RCCCQ)成立[19].因此條件(RCCCQ)弱于魯棒Slater條件.

下面借助條件(RCCCQ),給出問題(UP)的精確SDP松弛問題.

定理1對于問題(UP),假設(shè)F≠?.若條件(RCCCQ)成立,則

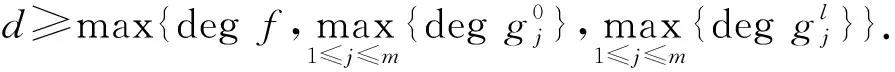
證明: 結(jié)合文獻(xiàn)[20]中定理3.1及文獻(xiàn)[21]中定理2.1的證明方法,易得結(jié)論成立.

推論1[9]對于問題(UP),假設(shè)F≠?.若魯棒Slater條件成立,則

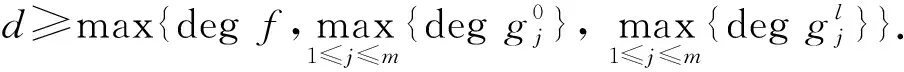
證明: 由注2中2)并結(jié)合定理1,易得結(jié)論成立.

注3由于條件(RCCCQ)弱于魯棒Slater條件,因此定理1改進(jìn)并推廣了文獻(xiàn)[9]中定理2.3的相關(guān)結(jié)果.

若不確定集Vj(j=1,2,…,m)為單點(diǎn)集,則易得如下結(jié)論.

推論2考慮如下平方和凸多項(xiàng)式優(yōu)化問題(P):

假設(shè){x∈n|gj(x)≤0,j=1,2,…,m}≠?,且f:n→與gj:n→(j=1,2,…,m)均為平方和凸多項(xiàng)式.若條件(CCCQ)成立,則

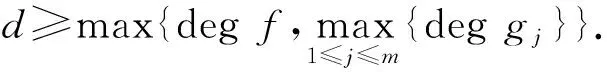
3 魯棒鞍點(diǎn)定理

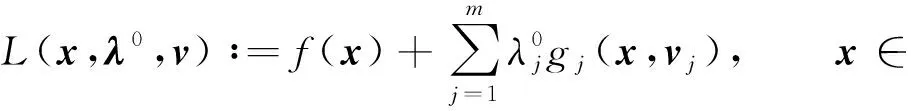
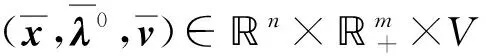
注4若不確定集Vj(j=1,2,…,m)為單點(diǎn)集,則問題(P)的Lagrange函數(shù)定義為

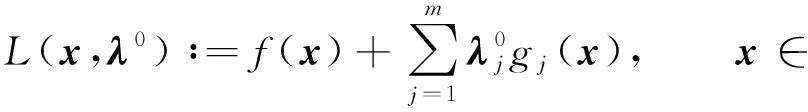
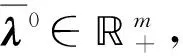
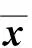
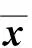
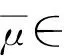
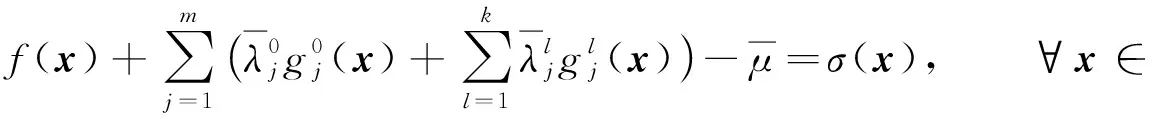
即對任意的x∈n,有

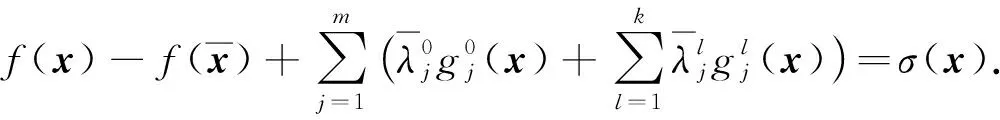
(1)

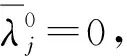
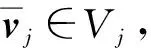
故結(jié)合式(1)可得

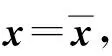
另一方面,對任意的x∈n,有

例1設(shè)m=1,k=2.令不確定集V1?2為

考慮不確定平方和凸多項(xiàng)式優(yōu)化問題(UP):

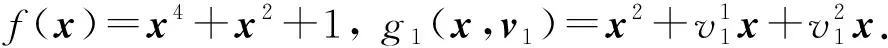
易證

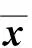
證明: 由注2中2)并結(jié)合定理2,易得結(jié)論成立.

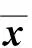
證明: 由注2中1)并結(jié)合推論2及定理2,易得結(jié)論成立.