迭代修正魯棒極限學習機

呂新偉，魯淑霞*

（1.河北省機器學習與計算智能重點實驗室（河北大學），河北 保定 071002；2.河北大學 數學與信息科學學院，河北 保定 071002）

0 引言

極限學習機（Extreme Learning Machine，ELM）自提出以來，已經成功應用于各種實際問題［1-5］，成為廣泛使用的機器學習工具之一。ELM 主要依賴于給定的訓練數據標簽，如基于L2范數損失函數的ELM［6］假設訓練標簽的誤差是一個正態分布；然而，實際問題中的訓練樣本不能保證誤差具有正態分布。此外，ELM 往往過分強調訓練過程中殘差較大的異常點，導致ELM 對異常點的敏感性和魯棒性較差。因此，構造能夠抑制異常點影響的魯棒極限學習機（Robust ELM，RELM）模型，在機器學習中是必要和有意義的。

ELM 的許多變體都致力于提高ELM 對異常點的魯棒性。引入正則化的極限學習機［7-9］通過在最小化目標函數中添加正則化項以減小結構風險，如加權極限學習機（Weighted ELM，WELM）［10］和魯棒極限學習機（RELM）［11］為訓練樣本分配適當的權值，但它們的性能在很大程度上依賴于權重估計的初始值。Chen 等［12］基于正則化項和損失函數的多種組合設計了迭代重加權極限學習機（Iteratively Re-Weighted ELM，IRWELM），并通過迭代加權算法實現。最近的一些研究則通過替換損失函數來增強極限學習機的魯棒性，例如使用Huber 損失函數［13］、L1范數損失函數［14］以及各損失函數的變體［15-16］等實現魯棒極限學習機，以減少異常點的影響；但它們仍然不夠穩健，因為這些損失函數受到殘差較大的異常點的影響。具有相關熵損失函數［17］和重標極差損失函數［18］的極限學習機改進版本傾向于構造有界和非凸損失函數，以提高對異常點的魯棒性。盡管這些損失函數具有良好的學習性能，但是求解該優化問題的方法過于復雜。有界的損失函數可以抑制殘差較大異常點的影響，迭代重加權正則化極限學習機（Iterative Reweighted Regularized ELM，IRRELM）［19］通過有界的L2范數損失函數抑制較大異常點的負面影響；但過多的異常點反過來會影響損失函數對異常點的判定，影響回歸結果。因此本文在有界L2范數損失函數的基礎上使用迭代修正方法，提出了一種用于回歸估計的魯棒極限學習機，以抑制異常點的負面影響，采用迭代加權算法求解魯棒極限學習機。在每次迭代中，為本輪認為是異常點的標簽重新賦值，并在每次迭代的過程中逐漸去除異常點的影響，增強極限學習機的魯棒性。

本文的主要工作包括：為減小極端異常點的影響，采用了有界損失函數，并在有界損失函數的基礎上提出了迭代修正魯棒極限學習機（Iteratively Modified RELM，IMRELM），讓這些殘差較大的異常點在迭代的過程中找到正確的標簽。實驗結果表明，當數據中的異常點數過多且殘差較大時，本文IMRELM 的結果優于對比的幾種魯棒極限學習機算法。

1 相關工作

1.1 極限學習機

假設有N個任意樣本，其中：xi∈Rd為輸入變量；yi∈R 是回歸估計中相應的目標。ELM 是一個單隱層神經網絡，具有L個神經元的ELM 的輸出函數可以表示為：

其 中：β=[β1，β2，…，βL]T為 ELM 輸出權 重；h(x)=[h1(x)，h2(x)，…，hL(x)]為隱含層矩陣；f(x)為回歸估計中相應的目標預測值。

ELM 求解以下優化問題來推導輸出權重β：

s.t.h(xi)β=yi-ei；i=1，2，…，N

其中：ei是訓練誤差；C是平衡模型復雜度的正則化參數。基于最優性條件，得到式（2）的最優解β：

其 中：數據的 真實標 簽y=[y1，y2，…，yN]T；H=[h(x1)，h(x2)，…，h(xN)}T是隱藏層輸出矩陣；I為適當大小的單位矩陣。

1.2 迭代重加權正則化極限學習機

為了減小L2范數損失函數對于殘差較大異常點的敏感性，IRRELM 使用了非凸L2范數損失函數。

其中：z是一個變量；θ是一個常數，θ是對大異常點的懲罰。g(z)的上界意味著損失在一定值后不會增加懲罰，并且它抑制了異常點的影響。

IRRELM 的優化模型為：

s.t.h(xi)β=yi-ei；i=1，2，…，N

在迭代重加權中，每個樣本的權重通過殘差由下式給出：

IRRELM 的第k次迭代解為：

在IRRELM 中，βk為第k次迭代中求得的隱層輸出權重；wk=diag(w1，w2，…，wN)為第k次迭代樣本權重。

算法1 IRRELM 算法。

2 迭代修正魯棒極限學習機

對于魯棒極限學習機，通常都是減小異常點的影響。但是基于L2范數損失函數的ELM 對異常點非常敏感，當數據中存在異常點時，異常點L2范數損失會很大。因此，選擇損失較小的數據進行訓練模型是有效的。為了避免過多異常點污染模型以及數據和資源的浪費，同時解決模型泛化能力不強的問題，在每次迭代中，對于那些殘差較大的數據進行修正。

為了處理異常點，本文提出了一種迭代修正魯棒極限學習機算法。

在IRRELM 中，優化模型又可以寫成：

令tik=1 -wik，提出以下損失函數：

優化模型為：

優化模型關于β求導并令其等于零，得到迭代修正魯棒極限學習機的解為：

其中：H=[h(x1)，h(x2)，…，h(xN)]T；wk=diag(w1，w2，…，wN)，tk=diag(t1，t2，…，tN)；C1、C2為正則化參數；I為適當大小的單位矩陣。

算法2 IMRELM 算法。

3 實驗與結果分析

為了研究IMRELM 的有效性，在人工數據集和真實數據集上進行了數值實驗。通過10 次交叉驗證和網格搜索方法選擇實驗參數。所有上述算法選擇的參數的范圍如下：參數kmax：{10i，i=2，3，4}，停止閾值p：{10i，i=-5，-4，…，1，2}，正則化參數C1、C2：{10i，i=-5，-4，…，4，5}。所有的實驗都在3.40 GHz 的機器上使用Pycharm 2019 進行。

比較算法是極限學習機（ELM）和一些魯棒極限學習機，包括加權極限學習機（WELM）、迭代重加權極限學習機（IRWELM）和迭代重加權正則化極限學習機（IRRELM）。在實驗中，使用sigmoid 激活函數g(x)=1/(1+exp(-x))。迭代加權的算法中的迭代次數為200，采用均方誤差（Mean-Square Error，MSE）作為估計標準：

其中：N是測試集的數量；yi、f(xi)分別是真實值和相應的預測值。通常，均方誤差越小，方法的性能越好。

3.1 IMRELM在人工數據集上的實驗

在不同異常點水平的人工數據集上進行實驗，結果給出了IMRELM 算法和其他算法的實驗結果，并通過統計測試比較了這些算法的性能。人工數據集來源于回歸問題中廣泛使用的函數，定義如下：

實驗在具有不同異常點水平的人工數據集上進行，并通過統計測試比較這些算法的性能。在實驗中，噪聲是［-10，10］上的均勻分布。按照數據的大小隨機生成不同占比的噪聲并添加到訓練集上。為了揭示IMRELM 算法的魯棒性，在不同水平異常點（包括0%、10%、20%、…、80%）數據集上分別進行對比實驗。在具有不同異常點水平的噪聲環境情況下，對比了幾個改進的極限學習機的魯棒性。對于每個異常點水平，在50 次獨立運行中進行實驗，以避免不公平的比較，并獲得了表1 中的均方誤差和標準差（Std）。

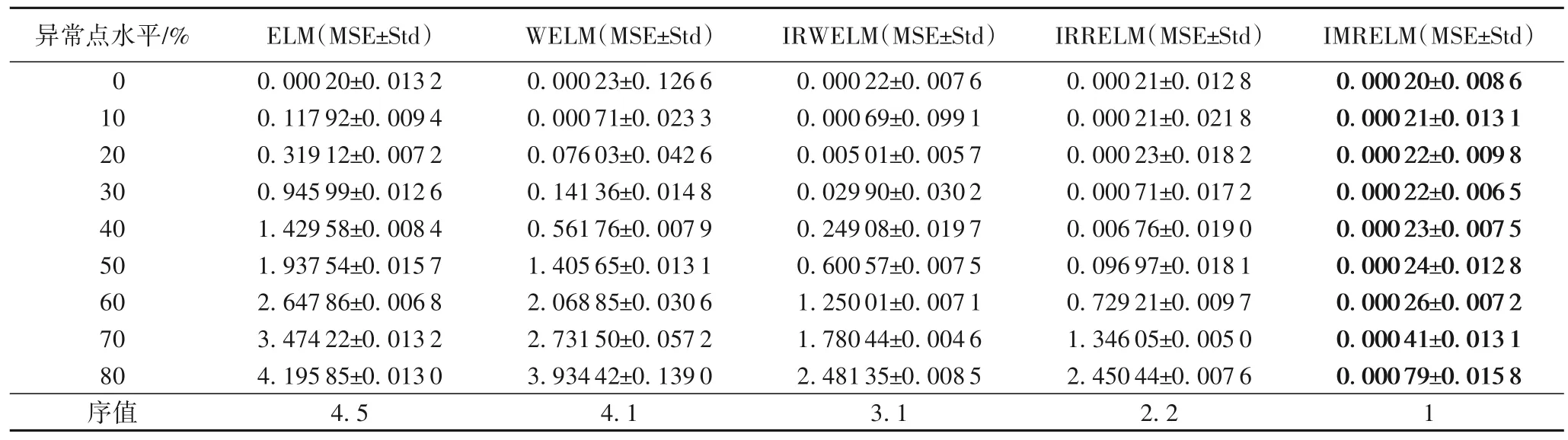
表1 具有不同異常點水平的人工數據集上的實驗結果Tab.1 Experimental results on synthetic datasets with different outlier levels

從表1 可以看出，在沒有異常點的情況下，經典ELM 表現出了很好的性能，具有最小的均方誤差值。IMRELM 的表現優于WELM、IRWELM 和IRRELM。在不同異常點水平的情況下，ELM 在所有水平上的表現都較差，反映了它對異常點的敏感性。

對于人工數據集，得到=26.244 和FF=21.520 2。在Friedman 測試中，如果α=0.05，得到Fα=2.157＜21.520 2。因此，拒絕“兩個算法性能相同”這一假設。繼續進行Nemenyi 檢 驗，α=0.1，qα=2.459，CD=1.832 8。如 表1 所示，IMRELM 和其他4 種魯棒性方法之間的排名差異為3，3，3，2 和1，因此，得出的結論是：IMRELM 的性能明顯不同于ELM、WELM、IRWELM，并且IMRELM 的性能最好。

為了更清楚地顯示這些算法的性能，圖1 顯示了在均勻分布噪聲下，5 種算法在不同異常點水平下的回歸曲線：當數據中沒有異常點時，5 種算法與原始曲線（SIN）擬合較好；當數據中異常點占比到30%時，WELM 開始偏離原始曲線；當數據中異常點占比到50%時，IRWELM 開始偏離原始曲線；當數據中異常點占比到60%時，IRRELM 開始偏離原始曲線。可以看出隨著數據中異常點水平的增加，ELM、WELM、IRWELM 和IRRELM 曲線部分偏離原始曲線，朝向異常點，而IMRELM 的曲線始終最接近原始曲線。

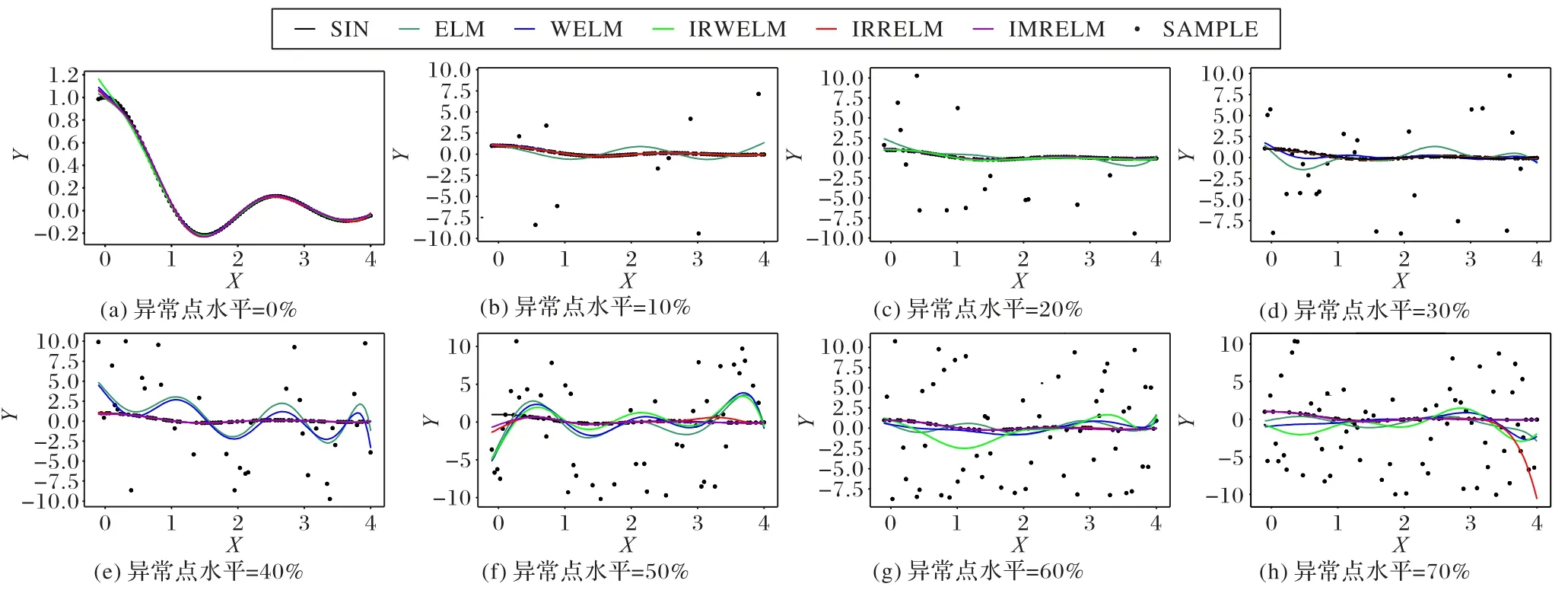
圖1 五種算法在不同異常點水平下的回歸曲線Fig.1 Regression curves of five algorithms under different outlier levels

3.2 IMRELM在真實數據集上的實驗

在12 個真實數據集上進行了進一步的實驗，以驗證IMRELM 在處理噪聲和異常點的有效性。在數據準備過程中，根據訓練樣本和測試樣本的數量，將每個數據集隨機分為兩部分（訓練集和測試集）（見表2）。在訓練集和測試集中，所有特征均歸一化為零平均值，標準殘差為1。真實數據集都來自UCI［20］。

表2 真實數據集Tab.2 Real datasets

從表3 可以看出，在沒有異常點的情況下，ELM 和極限學習機的其他4 種ELM 變體實現了相似的預測精度。當在具有異常點的數據集上進行訓練時，如均方誤差所反映的，ELM 的性能最差，它的性能隨著異常點水平的增加顯著下降，這表明ELM 對異常點不具有魯棒性；其他算法的預測精度要高得多，且IMRELM 在大多數情況下都優于其他算法。

表3 具有不同異常點水平的真實數據集上的實驗結果Tab.3 Experimental results on real datasets with different outlier levels

接下來通過Friedman 測試來討論這5 種算法在12 個真實數據集上的性能。表4 展示了幾種魯棒算法在實際數據集上的平均排名；表5 中展示了Friedman 測試的相關數據，其中Δ（IMRELM-ELM）表示IMRELM 和ELM 的序值差。在真實數據集上FF均大于Fα，因此，拒絕在這12 個真實數據集上的“兩個算法性能相同”這一假設。因為Δ（IMRELMELM）、Δ（IMRELM-WELM）的值均大于CD值1.832 8，所以IMRELM 與ELM、WELM 和IRWELM 的性能有明顯的差異。Δ（IMRELM-IRRELM）、Δ（IMRELM-IRWELM）的值均 在1左右。

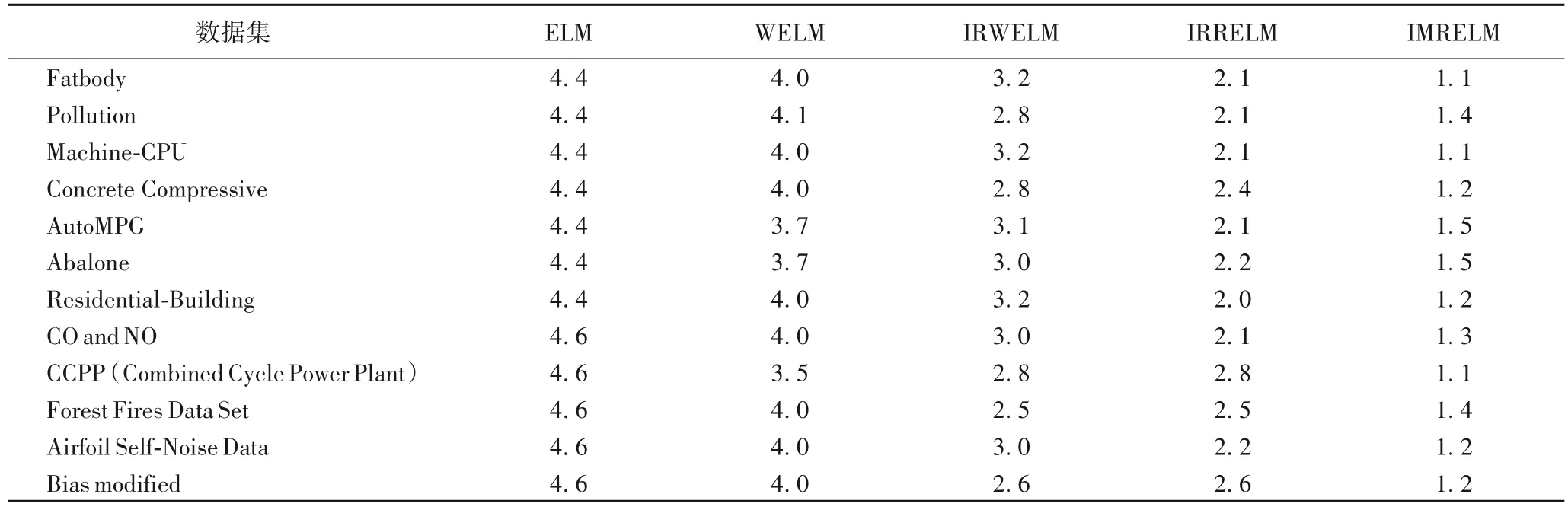
表4 五種算法在12個真實數據集上的平均序值Tab.4 Average order values of five algorithms on 12 real datasets

綜上，可以得到IMRELM 在含有異常點的數據集上的預測精度最好。

4 結語

在實際應用的真實數據集中往往含有離群值，這會導致ELM 的泛化性能較差。為了抑制異常點的負面影響，提高ELM 的魯棒性，提出了迭代修正魯棒極限學習機（IMRELM）算法，使用迭代重加權的方法進行優化。IMRELM 在每次迭代中將離群值的權值設為0，并重新進行標簽賦值。因此，最小化目標函數時不涉及離群值，可以增強ELM 的魯棒性。在1 個人工數據集和12 個不同離群值水平的真實數據集上的對比實驗結果表明，IMRELM 具有良好的預測精度和魯棒性。但目前IMRELM 中只考慮了原始ELM 中的L2范數損失函數，在未來的工作中也可以拓展到其他ELM 變體中的損失函數，如Huber 損失極限學習機、L1范數損失極限學習機和鉸鏈損失極限學習機，以獲得穩健的極限學習機模型。