一題“多”解 多解歸“一”
——從一道矩形的翻折問題談起

文／金明

矩形的翻折問題一直是中考壓軸題的高頻考點，同學們遇到這類問題時常常無法將已知條件和數學知識建立聯系，更不知從哪方面入手。現借助一道矩形內翻折問題的變式拓展，幫助同學們熟悉相關數學模型。

例題 如圖1，在矩形ABCD中，AB=4，BC=6，點E為BC的中點，將△ABE沿AE折疊，使點B落在矩形內的點F處，連接CF，求CF的長。

圖1

【分析】由EF=EC=EB可構造出直角三角形BFC，即將求線段CF的長轉化為“解直角三角形”。連接BF交AE于點K，如圖2，由“翻折”的性質得到垂直，再由已知直角（∠ABE=90°）得到常見的“母子相似模型”（∠ABE=∠BKA=90°），其常用的結論是“三組直角三角形相似”和“角的等量關系”。本題也可以利用△ABE∽△BFC進行求解，或利用中位線先求KE，再求CF。

【簡解】如圖2，連接BF交AE于點K。

圖2

變式1 如圖3，連接BF并延長，交線段AD于點G，求線段FG的長。

圖3

變式2 如圖4，延長EF交線段AD于點G，求線段FG的長。

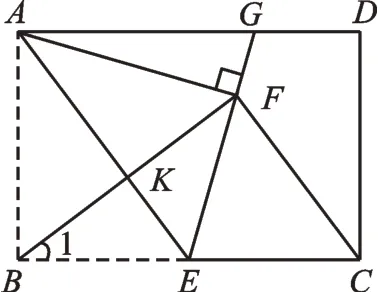
圖4

【分析】變式2的出發點是想讓同學們體會“角平分線”“平行”“等腰三角形”在矩形翻折問題中的應用，這里稱之為“平行+角平分線模型”。當然，除此之外還有其他不同的方法。

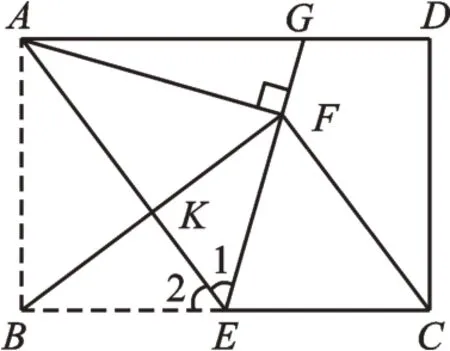
圖5

圖6

圖7

圖8

圖9

方法6（三角形全等）：如圖10，過點G作GH⊥BC于點H。易證四邊形AGHB為矩形，則GH=AB=AF，∠AGH=∠AFG=90°。由AG//BH，得∠AGF=∠GEH，易證△AFG≌△GHE。設GF=x，則GE=3+x，EH=GF=x，GH=AB=4。在Rt△GEH中，EH2+GH2=EG2，則x2+42=（3+x）2，解得x=，則GF。

圖10

方法1 與方法2 的突破口在“等腰三角形”，可通過平行線+角平分線產生的角度數量關系得到一組相等的角，進而得到“等腰三角形”。方法1 側重等腰三角形的“腰相等”，通過設未知數，利用勾股定理列方程求解；方法2 側重等腰三角形的對稱性，利用“三線合一”的性質求出相應的線段，再利用“三角函數”求解線段。

方法3、方法4 利用相似進行求解。在方法3 中，已知EF，求GF，觀察到AD//BC，進而通過延長線段，構造常見的“8 字型”相似求解；在方法4 中，發現圖中不需要添加輔助線，便得到EF和GE所在的三角形相似（△AGE∽△CEF），進而得解。

方法5 與方法6 是利用解決以矩形為背景的問題中最常見的方法（化斜為直）來解決問題，其本質是通過作垂直構造直角三角形，利用直角三角形特殊的邊角關系進行求解。

至此，雖一題多解，但通過多種方法的總結與內化，我們發現，萬變不離其宗，多解可以歸一，“平行+角平分線模型”“三角形相似”“化斜為直”是解決矩形翻折問題重要的突破口。