表面織構對角接觸球軸承潤滑性能的影響*

王保民 吳 艷 閆瑞祥 房文博

(蘭州理工大學機電工程學院 甘肅蘭州 730050)

油氣潤滑憑借優異的潤滑性能，被廣泛應用于高速角接觸球軸承，而軸承腔內油氣兩相的分布對軸承的潤滑性能有很大的影響[1]。表面織構技術是指在摩擦副表面加工出具有一定規則的微小凹坑或者微凸體，這些微凹坑或微凸體不僅可以存儲潤滑油，還能夠容納磨屑，能有效提高摩擦副的潤滑性能[2-3]。

表面織構最早于1966年由HAMILTON等[4]提出。隨著科技和制造業的不斷發展，表面織構技術引起了國內外學者的廣泛關注，其中ETSION等[5-7]在機械密封方面的研究最為引人注目。李超等人[8]通過在渦旋壓縮機止推軸承表面設計微織構，研究了微織構參數、形狀以及排列方式對潤滑效果的影響。趙遠方[9]利用三維光纖打標機加工出不同排列方式凹坑織構，在自主搭建的摩擦磨損實驗臺上測量了摩擦副表面力矩大小，結果表明無織構表面磨損遠大于微織構表面，且軸向間隔分布織構減磨效果最好。以滾動軸承滾針與外圈為研究對象，張迪[10]分析了不同轉速下表面微織構對于軸承摩擦學性能的影響。VIDYASAGAR等[11]研究發現，在低載荷條件下，在滾動軸承內圈表面布置織構可以有效降低摩擦扭矩和整體振動。華希俊等[12]基于彈性流體動壓潤滑機制，分析了圓柱滾子軸承微織構幾何參數以及工況對潤滑油膜平均量綱一壓力的影響。張宇等人[13]研究了深溝球軸承滾動體與滾道橢圓接觸的穩態和瞬態潤滑問題，結果表明，表面粗糙度對摩擦因數影響不大，當表面粗糙度一定時，表面幾何形狀對摩擦因數影響較小。劉小君等[14]通過試驗發現，在脂潤滑條件下，將表面高度參數、功能參數和特征參數這幾種表面形貌參數結合對關節軸承表面形貌進行表征，更有利于關節軸承表面形貌的摩擦學設計。MARIAN等[15]基于熱流體動力學模型分析了帶有方形凹坑的止推軸承潤滑油膜厚度與承載能力的關系，并對織構幾何參數進行了優化。金志浩等[16]以81107-TN推力圓柱滾子軸承為研究對象，通過萬能摩擦磨損試驗機進行試驗，結果表明在干摩擦狀態下，凹坑型織構可以降低磨損量，并得出了最佳的織構參數。BHARDWAJ等[17]以推力球軸承為研究對象，通過實驗發現，在推力球軸承的外圈周向布置微凹槽，滾道表面的磨損量有所減小，且油潤滑條件下，潤滑效果更佳。

現有研究表明，表面織構可以有效地改善圓柱滾子軸承以及推力軸承的摩擦學特性。但是針對表面織構化高速角接觸球軸承在油氣潤滑狀態下的潤滑性能的研究較少。本文作者以SKF 7210C高速角接觸球軸承為研究對象，通過在角接觸球軸承的內圈滾道上設計表面織構，運用多重坐標系法，建立點接觸彈流潤滑理論分析模型，基于氣液兩相流理論，分析表面織構的形狀對角接觸球軸承腔內油相體積分數的影響，并進一步探究表面織構的結構參數對角接觸球軸承腔內油相體積分數的影響。研究結果為改善角接觸球軸承在油氣潤滑狀態下的潤滑性能提供了理論依據。

1 數值計算模型

1.1 基本方程

角接觸球軸承由內圈、外圈、滾動體、保持架四部分組成，其中，軸承內圈、保持架以及滾動體均以各自的角速度進行公轉，滾動體除了公轉以外，還有沿著自身軸線的旋轉運動，運動方式比較復雜。為了能夠更加準確地描述其運動方式，對其分別使用慣性坐標系和旋轉坐標系，即多重參考坐標系(Multiple Reference Frame，MRF)進行描述。運動方式如圖1所示。

圖1 多重參考坐標系Fig.1 Multiple reference frame

在軸承運動過程中，軸承外圈為靜止壁面，滾動體、內圈、保持架均為角速度為ω繞X軸旋轉的旋轉壁面，同時，滾動體沿著自身軸線以角速度ω′做旋轉運動，其轉速由計算公式(1)和(2)確定。

(1)

(2)

γ=Dcosα/dm

(3)

式中：ni為角接觸球軸承內圈轉速，r/min；nm為保持架與滾動體公轉的轉速，r/min；nR為滾動體自轉速度，r/min；dm為節圓直徑，mm；D為滾動體直徑，mm；α為角接觸球軸承的接觸角。

角接觸球軸承在運動過程中，滾珠與滾道之間的接觸方式為點接觸，因此，在計算過程中，基于點接觸彈流潤滑理論進行求解[18]，點接觸彈流潤滑Reynolds方程的形式為

(4)

式中：p表示油膜壓力；h表示油膜厚度；η表示潤滑油黏度；x表示潤滑卷吸速度方向的坐標；y表示垂直于卷吸速度方向的坐標；u表示卷吸速度，

(5)

其中，uA和uB分別為A、B兩個曲面的表面速度。

在角接觸球軸承流體域的質量、動量及能量守恒方程可描述為

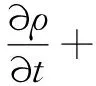
(6)

(7)

(8)

1.2 幾何模型及網格劃分

文中以SKF 7210C角接觸球軸承為研究對象，其結構參數如表1所示。

表1 SKF 7210C角接觸球軸承結構參數Table 1 Structural parameters of SKF 7210C angular contact ball bearing

文中主要研究在內圈滾道布置織構對角接觸球軸承潤滑性能的影響，其結構如圖2所示。

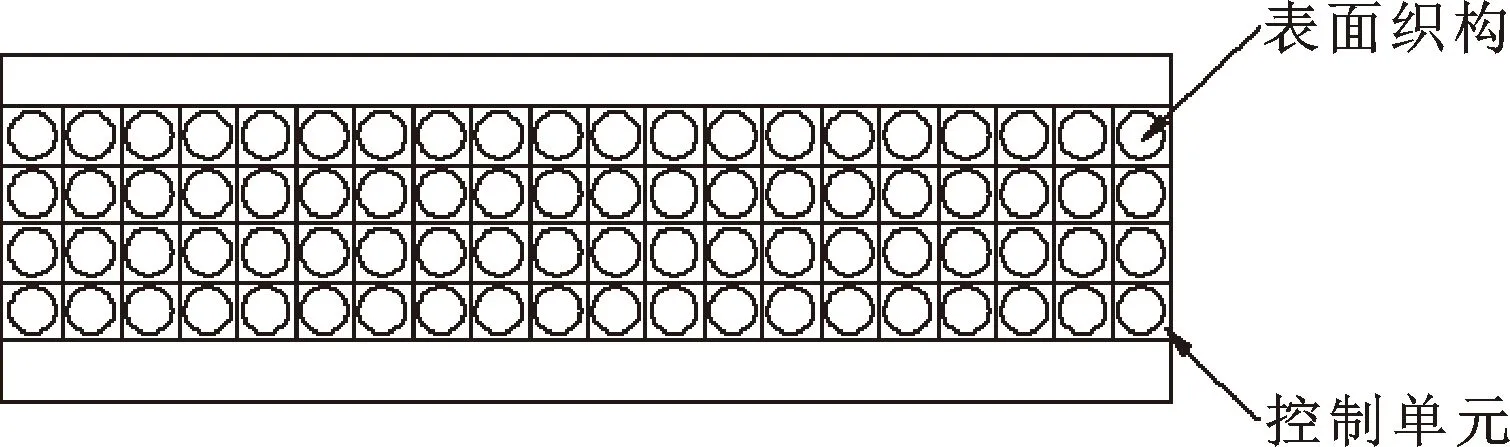
圖2 內圈表面織構結構示意Fig.2 Schematic of inner ring surface texture structure

運用ICEM CFD對軸承腔體進行結構化網格劃分，最終得到網格數量為1 648 738，質量達到0.5以上，符合計算要求，其網格模型如圖3所示。

圖3 軸承腔流體域網格模型Fig.3 Fluid domain mesh model of bearing cavity

1.3 邊界條件及求解方法設置

當軸承高速旋轉時，軸承腔內油氣兩相處于湍流狀態。因此，采用RNGκ-ε模型作為湍流求解模型，壁面函數選用標準壁函數。由于軸承腔內氣體流動的馬赫系數很低，因此認為氣體是不可壓縮的，黏性系數是恒定的。入口為環形流入口，氣相入口為壓力入口，壓力為0.25 MPa，油相入口為速度入口，速度為10 m/s，流體出口為壓力出口，壓力為標準大氣壓。軸承轉速為8 000 r/min。油氣材料參數如表2所示。

表2 油氣材料參數Table 2 Oil and gas material parameters

2 仿真結果與分析

2.1 織構形狀對軸承腔內油相體積分數的影響

為分析織構形狀對軸承腔內油相體積分數的影響，在軸承腔內圈滾道表面分別排布如圖4所示的4種不同形狀的織構。其中，圖4(a)所示為長溝槽織構，軸向分布1個弧長為6 mm的長溝槽形織構；圖4(b)所示為短溝槽織構，軸向分布2個弧長為3 mm的短溝槽織構；圖4(c)所示為矩形織構，軸向分布4個弧長為1.5 mm的矩形織構；圖4(d)所示為圓柱形織構，軸向分布5個截面弧長為1.236 mm的圓柱形織構。織構徑向深度均為20 μm，軸向間距為4.54°，周向間距為2.994°，每一個織構微單元面積都為6 mm2，織構結構如圖5所示。

圖4 不同形狀的織構排布示意Fig.4 Schematic of different shape texture arrangement：(a)long groove texture；(b)short groove texture；(c)rectangular texture；(d)cylindrical texture

圖5 織構結構示意Fig.5 Schematic of texture structure

在軸承內圈溝道上布置4種不同類型的表面織構，軸承腔內平均油相體積分數如圖6所示。與無織構相比，織構化內圈軸承腔內油相體積分數均有所提高，其中，長溝槽形織構對軸承腔內油相體積分數的影響最大。這是由于微凹坑內壁面與潤滑油之間的黏附力可以抵消因主軸轉速過高而產生的離心力，所以與普通表面相比，織構化內圈能夠存儲更多的潤滑油，當滾珠與內圈處于乏油潤滑狀態時，凹坑織構可以釋放潤滑油，使滾珠與內圈能夠充分潤滑。這與文獻[10]與文獻[18]得出的結論基本一致，表明表面織構可以改善軸承的潤滑性能。

圖6 不同織構形狀下軸承腔內油相體積分數Fig.6 Volume fraction of oil phase in bearing cavity under different texture shapes

2.2 織構深度對軸承腔內油相體積分數的影響

從圖6可以得出，長溝槽形織構對軸承腔內油相體積分數的影響最大。因此，文中以長溝槽形織構為例，分析其結構參數對軸承腔內油相體積分數的影響。

圖7示出了軸承腔內油相體積分數隨溝槽深度變化趨勢。溝槽寬度不變，軸承腔內油相體積分數隨著溝槽深度的增加先增大后減小，當織構深度為12 μm時，軸承腔內油相體積分數達到最大值。這是由于當織構深度較小時，凹坑內壁面與潤滑油之間的黏附力不能抵消離心力的作用，導致軸承腔內油相體積分數較小；當織構深度較大時，由于較高的織構側壁面會阻擋潤滑油的流通，使潤滑油堆積在織構內，從而減小了織構產生的流體動壓效應，使潤滑不均勻。當織構深度為12 μm時，軸承腔內油相體積分數比無織構增加了約68.8%。這與文獻[18]得出的結論基本一致。

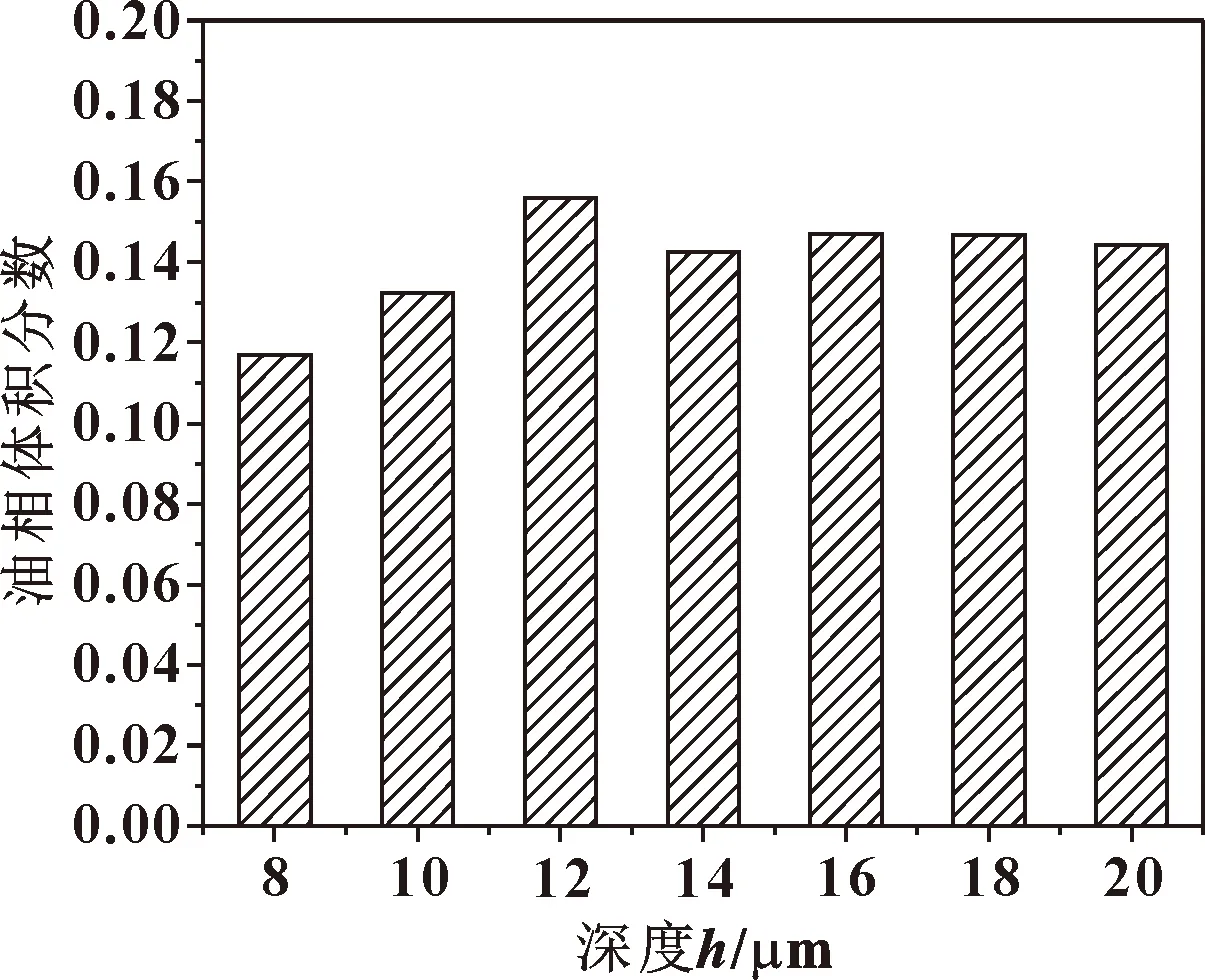
圖7 不同織構深度下軸承腔內油相體積分數Fig.7 Volume fraction of oil phase in bearing cavity under different texture depth

2.3 織構面積率對軸承腔內油相體積分數的影響

圖8示出了軸承腔內油相體積分數隨織構面積率的變化趨勢。

圖8 不同織構面積率下軸承腔內油相體積分數Fig.8 Volume fraction of oil phase in bearing cavity under different texture area ratio

當織構寬度不變，深度為12 μm時，軸承腔內油相體積分數隨溝槽面積率的增大先增大后減小，當織構面積率為0.47時，軸承腔內油相體積分數最高。這是由于面積率較小時，織構之間的距離較遠，當潤滑油進入織構后滾珠與內圈的距離突然變大，導致油膜破裂，壓力迅速降低，經過織構后，距離減小，壓力變大，形成額外的正壓力；當面積率變大時，織構之間的距離減小，相鄰織構相互影響，使正壓力降低，降低了流體動壓效應，導致正壓力降低，使軸承腔內油相體積分數低。這與文獻[18]得出的結論基本一致。

2.4 織構寬度對軸承腔內油相體積分數的影響

當織構深度為12 μm，面積率為0.47時，軸承腔內油相體積分數隨織構寬度的變化如圖9所示。可以看出，軸承腔內油相體積分數隨著織構寬度的增加而增大，當織構寬度大于1 mm時逐漸趨于穩定。這是由于當織構寬度增大時，溝槽內可以儲存更多的潤滑油，隨著主軸旋轉，凹坑內儲存的潤滑油可以不斷被擠出，增大了軸承腔內油相體積分數，提高潤滑效果。當織構寬度大于1 mm時，正負壓區不再發生變化，軸承腔內油相體積分數也逐漸達到平穩狀態。雖然文中織構形狀與文獻[18]不同，但是最終得出的結論基本一致。

圖9 不同織構寬度下軸承腔內油相體積分數Fig.9 Volume fraction of oil phase in bearing cavity under different texture width

2.5 織構化參數對軸承氣簾效應的影響

當軸承進油量為7.5 mL/h，進氣壓力為0.25 MPa，軸承轉速為8 000 r/min時，選取油氣入口沿旋轉方向后側滾珠徑向最大截面，分析織構參數對氣簾效應的影響。圖10(a)所示為無織構軸承截面流線圖，圖10(b)所示為織構深度為12 μm、寬度為1 mm、面積率為0.47的織構化內圈軸承截面流線圖。可以看出，由于空氣和高速旋轉的滾動體、內圈表面之間的摩擦，油氣兩相流在入口側滾動體和內圈接觸區域附近產生漩渦，形成氣簾效應。在軸承內圈布置織構后，空氣與軸承內圈直接的摩擦增大，使滾珠與內外圈之間的漩渦更加明顯，氣簾效應加劇。

圖10 軸承截面流線Fig.10 Streamline of bearing section：(a)non- textured bearing；(b)textured bearing

2.6 寬度和面積率對軸承腔內油相體積分數的耦合影響

圖11示出了織構深度為12 μm時，織構寬度與面積率對軸承腔內油相體積分數的耦合影響。可以看出，當織構深度一定時，不同面積率下角接觸球軸承腔內油相體積分數隨著織構寬度的增加先逐漸增大后趨于穩定，同一織構寬度下角接觸球軸承腔內油相體積分數隨著面積率的增加先增大后減小；當織構面積率為0.47，寬度為1.5 mm時，軸承腔內油相體積分數達到最大值。

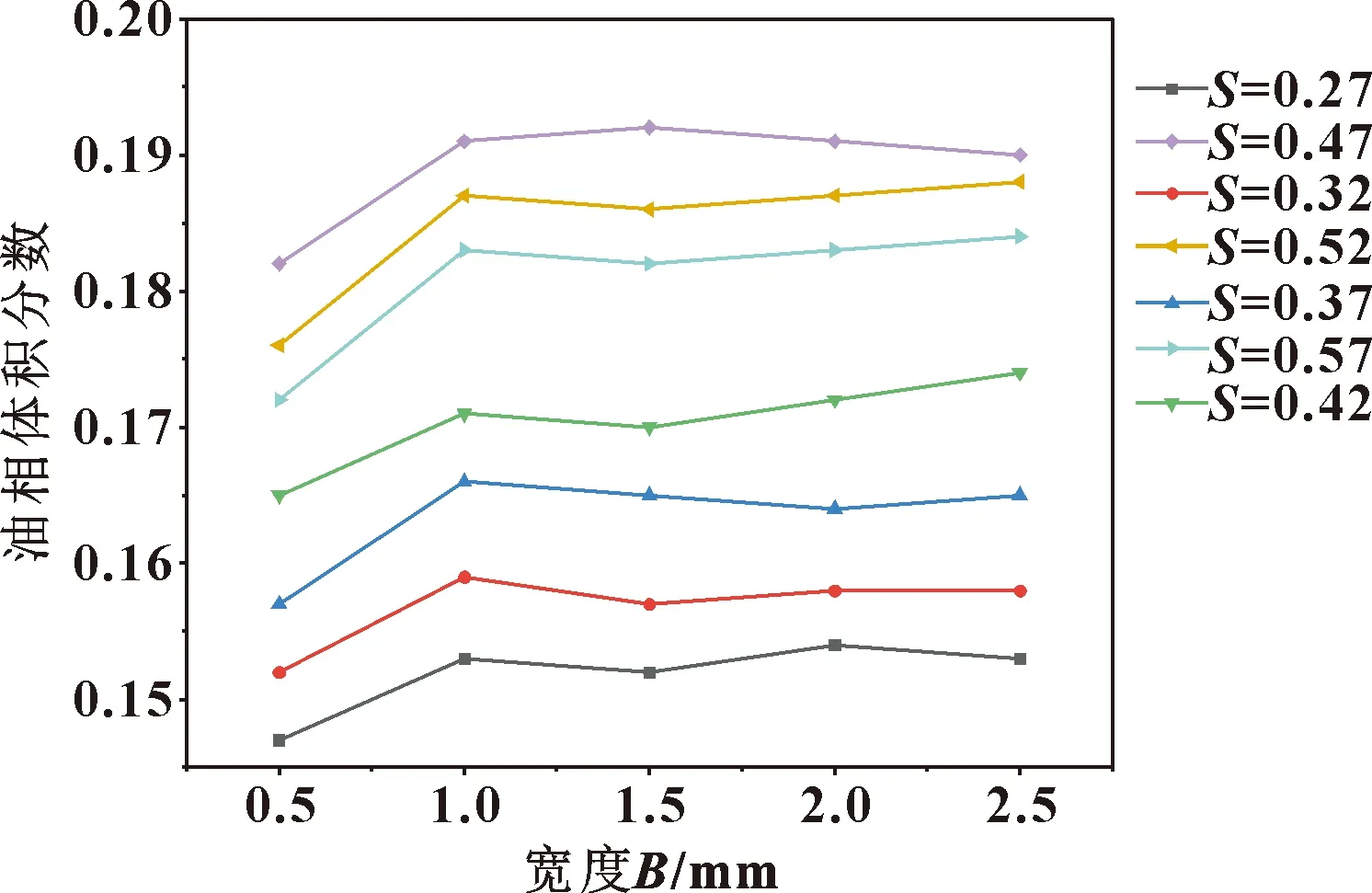
圖11 織構寬度與面積率對軸承腔內油相體積分數的耦合影響Fig.11 Coupling effect of texture width and area ratio on oil volume fraction in bearing cavity

3 結論

(1)與無織構表面相比，內圈織構能顯著提高角接觸球軸承腔內油相體積分數，且長溝槽形織構產生的潤滑效果更加明顯。

(2)當長溝槽織構寬度與面積率不變時，軸承腔內油相體積分數隨著織構深度的增加先增加后減小，在深度為12 μm時達到最佳值；當長溝槽織構深度為12 μm，寬度不變時，軸承腔內油相體積分數隨著面積的增加先增加后減小，在面積率為0.47時達到最佳值；當長溝槽織構深度為12 μm，面積為0.47時，軸承腔內油相體積分數隨著織構寬度的增加先增加后逐漸趨于平穩。

(3)在軸承內圈滾道上布置織構，使氣簾效應進一步加劇。

(4)織構深度一定時，軸承腔內油相體積分數受織構寬度和面積率的共同影響。當織構深度為12 μm，織構面積率為0.47，寬度為1.5 mm時，軸承腔內油相體積分數達到最大值。