M?bius幾何中的多分量Camassa-Holm方程
覃 慧, 王 寶
M?bius幾何中的多分量Camassa-Holm方程
覃 慧, 王 寶*
(寧波大學 數學與統計學院, 浙江 寧波 315211)
研究了一般M?bius幾何中的曲線流, 證明了一類多分量的Camassa-Holm方程等價于M?bius幾何中的一個不變曲線流, 此方程是兩分量Camassa-Holm方程的多分量推廣, 也可以看成是一類多分量KdV系統的對偶可積系統. 最后得到了此方程的一個退化情形的尖峰孤子解.
不變曲線流; M?bius幾何; Camassa-Holm方程; 多分量Camassa-Holm系統; 尖峰孤子解
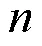
本文在文獻[12]的基礎上把M?bius幾何的李代數形式進一步推廣, 證明一個(1++)分量的KdV方程和(1++)分量的Camassa-Holm方程可以從這一般M?bius幾何中的曲線流中得到. 利用伸縮變換進一步研究這個多分量Camassa-Holm方程的柯西問題, 最終得到一個退化情形的尖峰孤子解.
1 一般M?bius幾何中的可積方程
2006年, Sanders等[9]研究了以下李代數確定的M?bius幾何中的曲線流,



文獻[12]從Sanders等[9]的工作出發, 提出研究由更一般的李代數
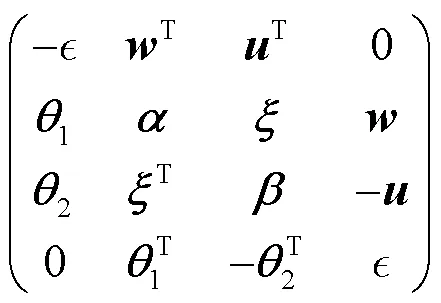
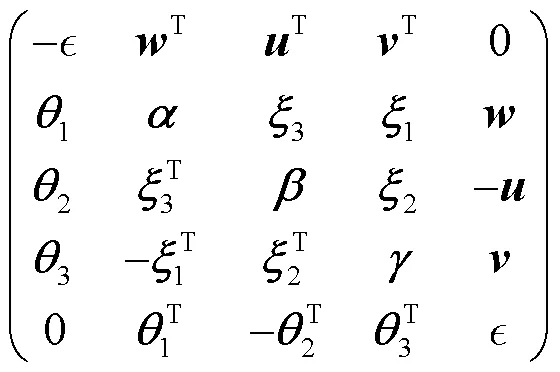

引入Lorentz群

和M?bius群
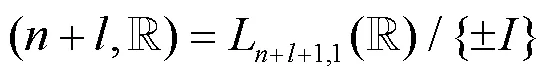
設
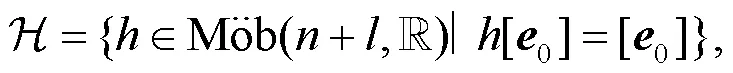
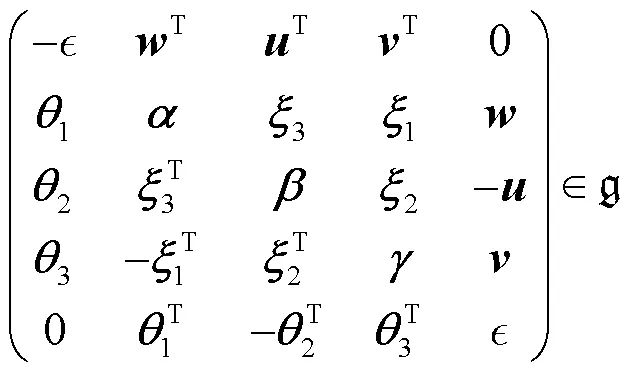


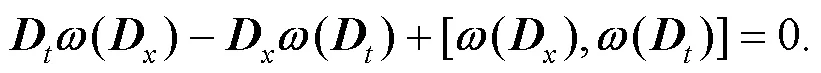
將式(3)代入式(4), 得到以下方程:
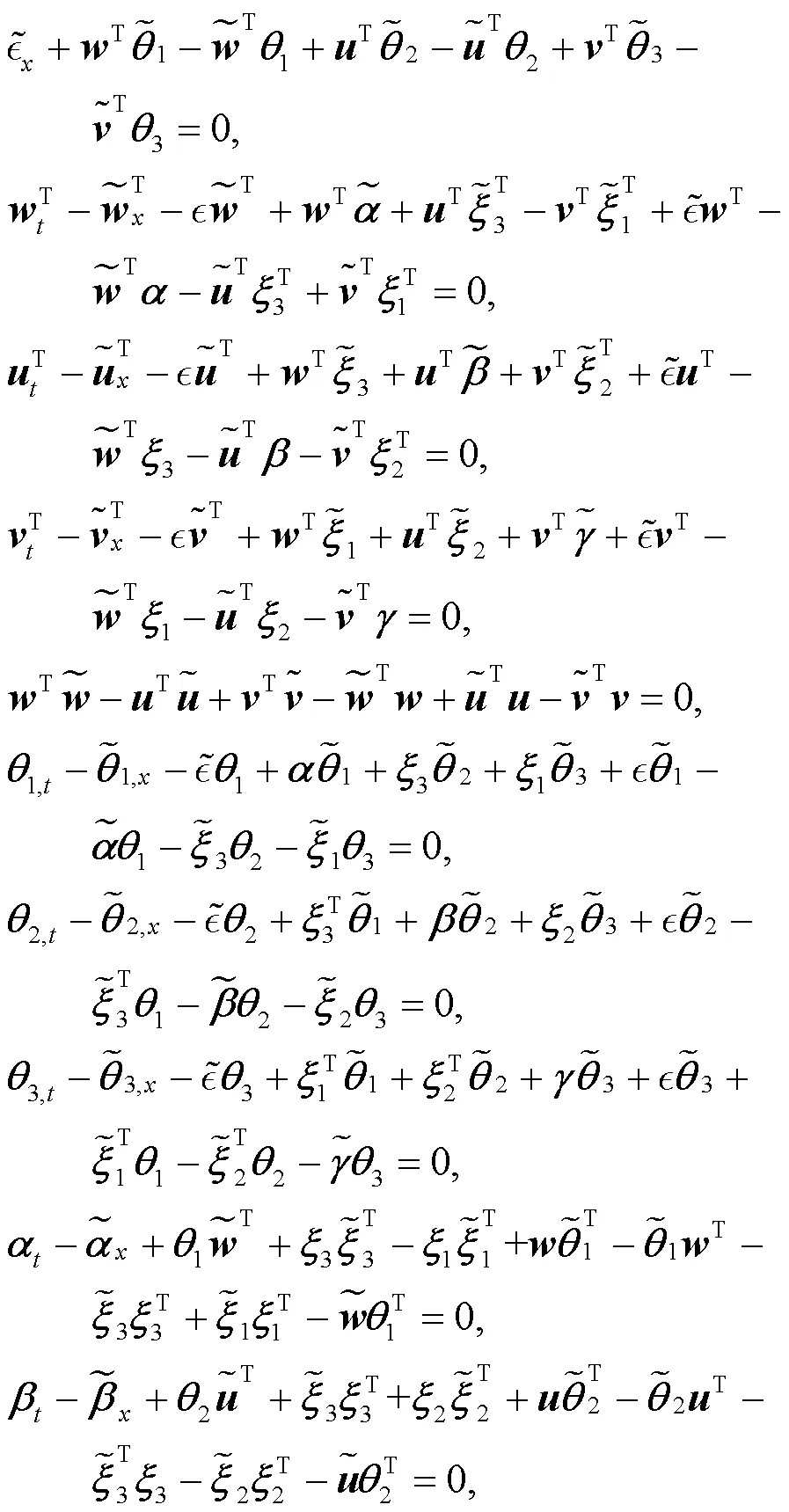
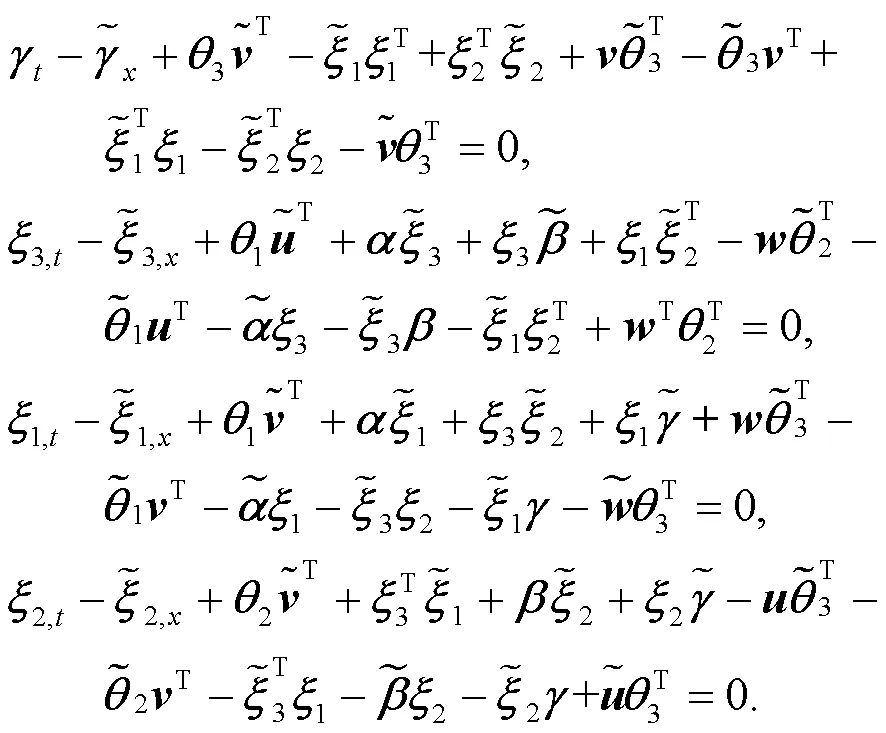
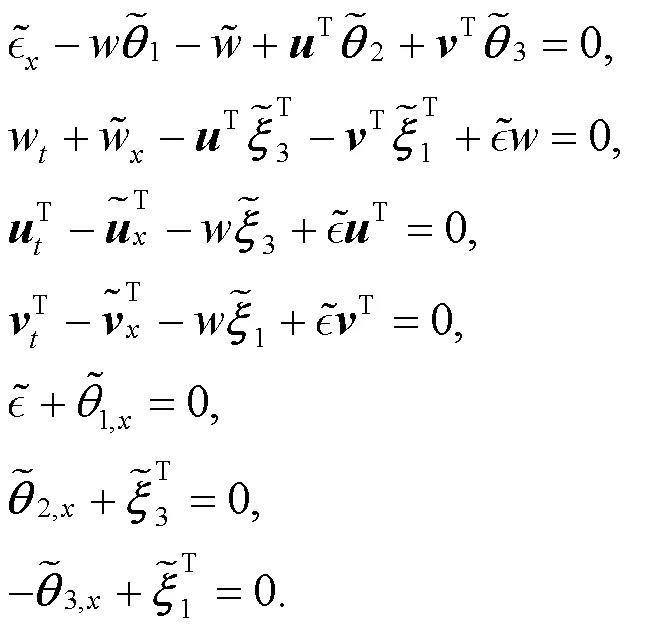
顯然, 方程有以下解:
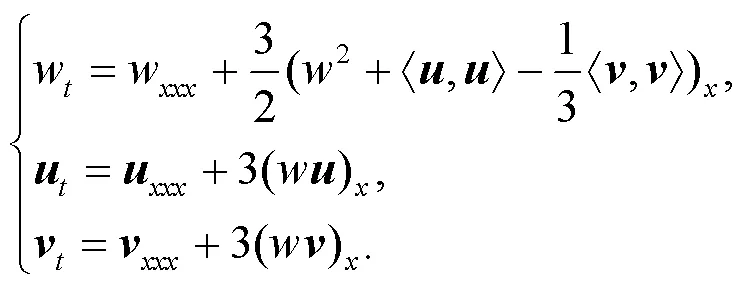
對此方程組可求得如下解:

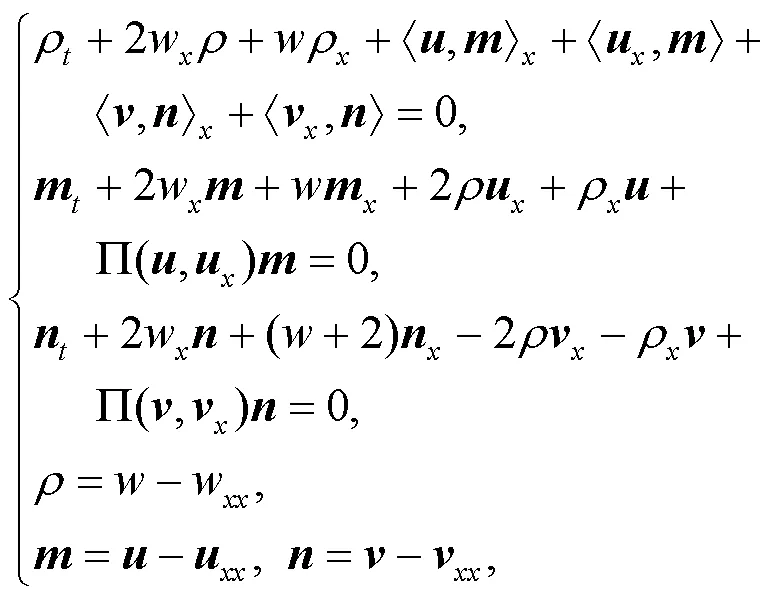
2 (1+n+r)分量CH方程的尖峰孤波解
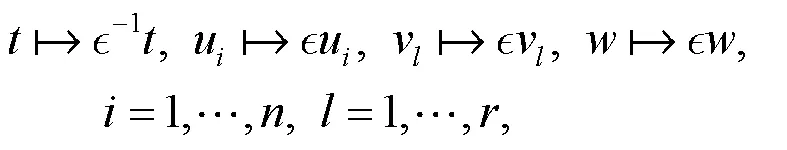
代入方程(7)得到以下方程:
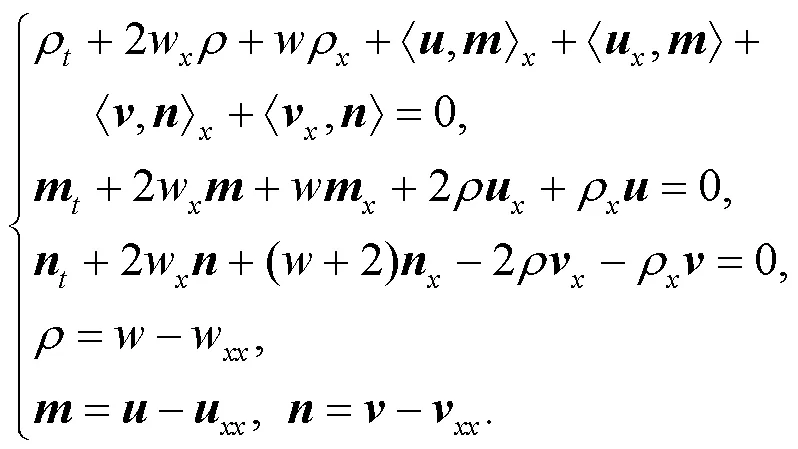
本節將研究方程(8)柯西問題
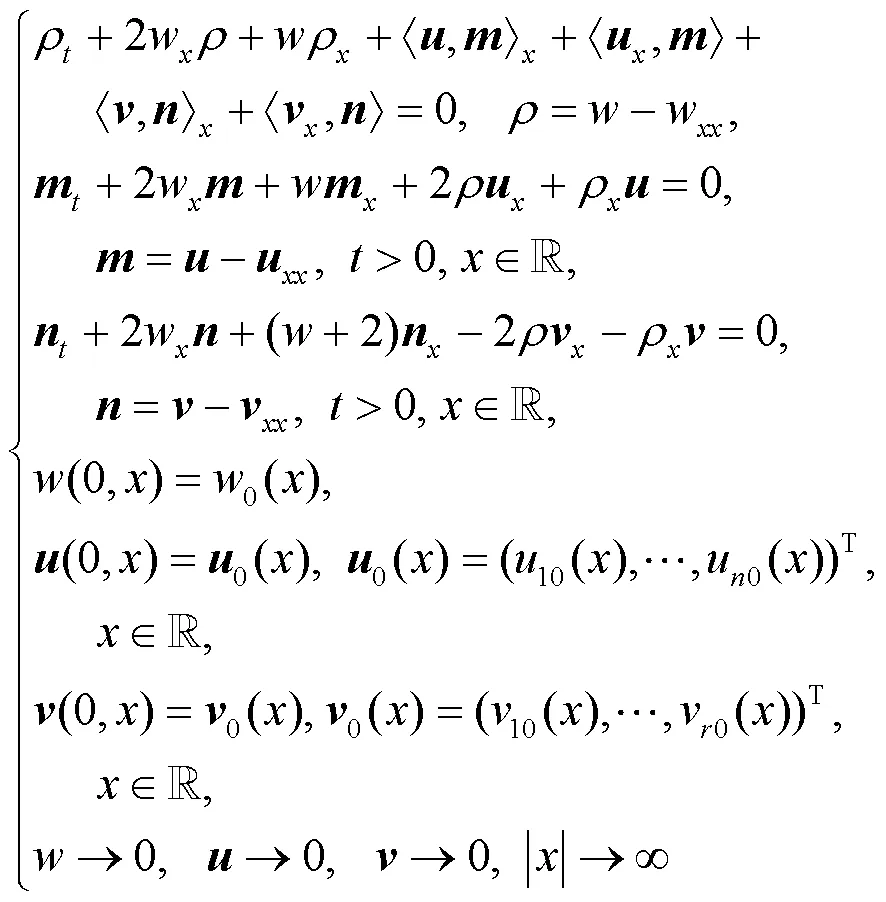
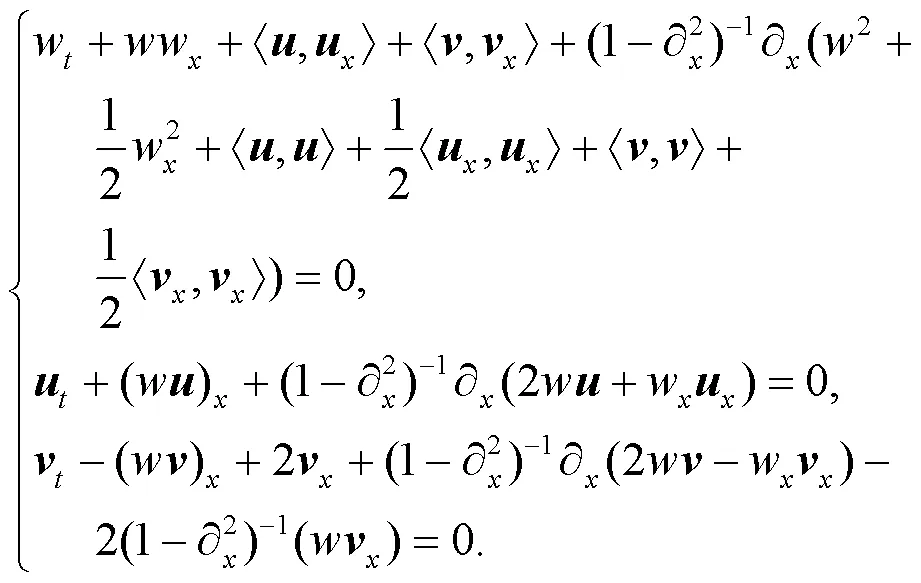
注意到
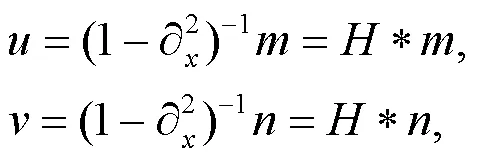
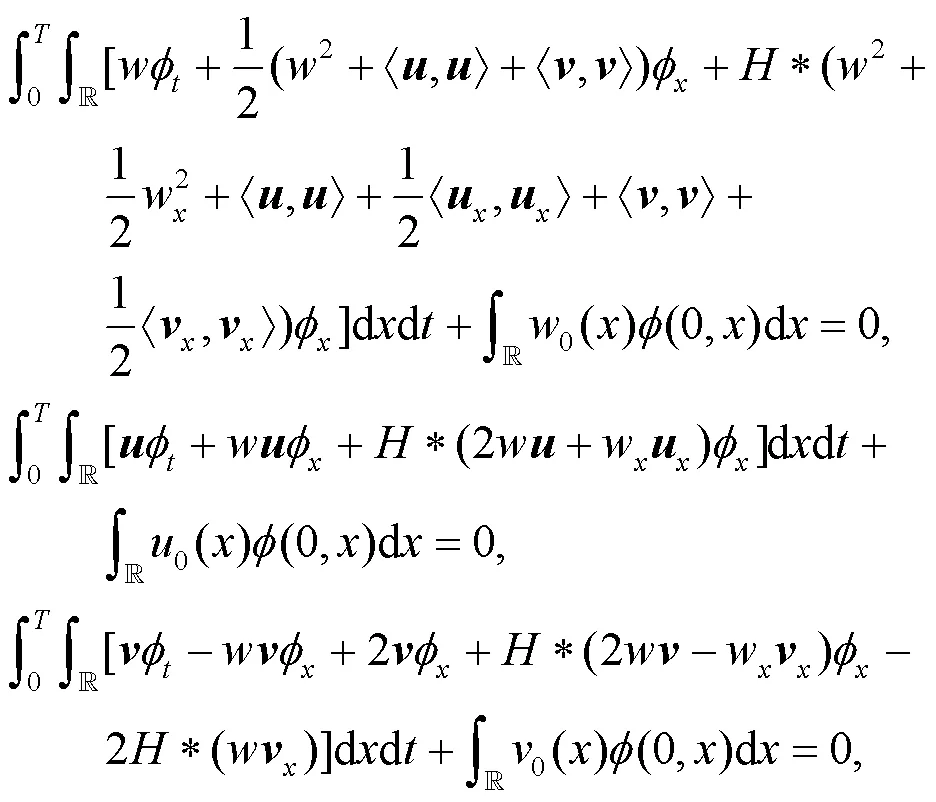
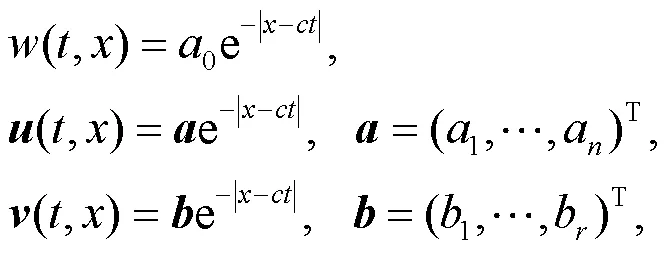
且滿足條件

的表達式是方程(9)的全局弱解.
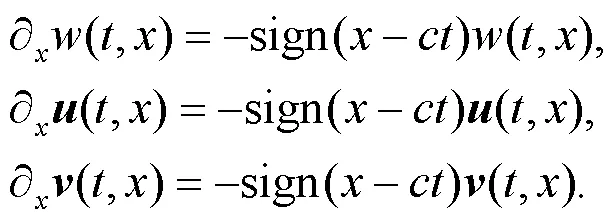
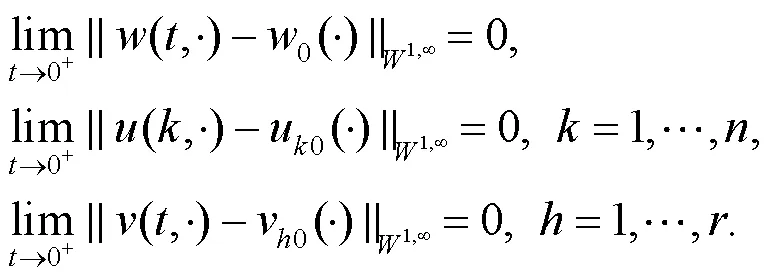


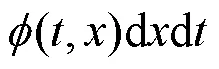
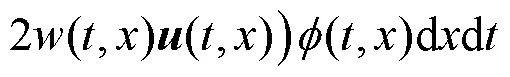
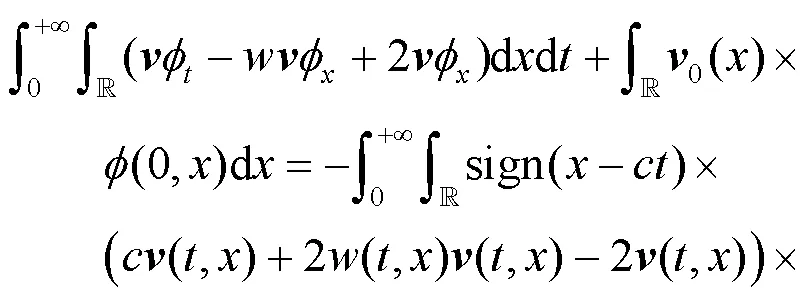
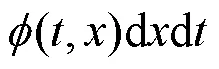
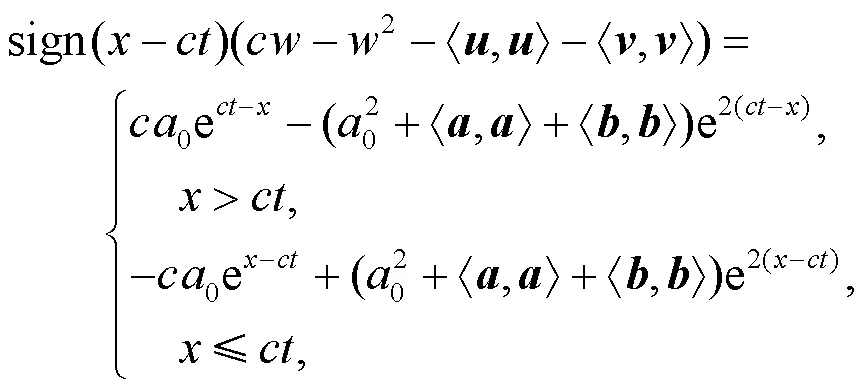
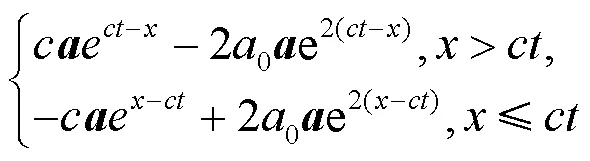
和


另一方面, 由式(10)有
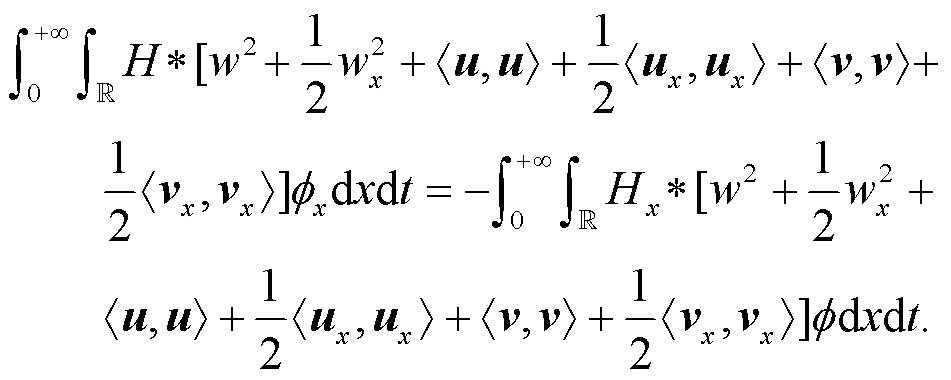
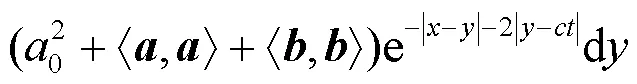
直接計算得

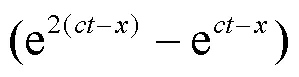

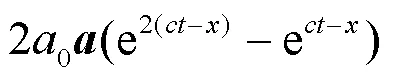

和
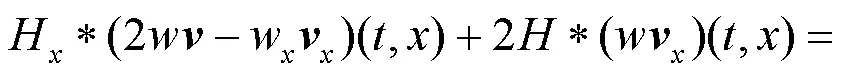
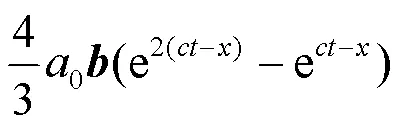
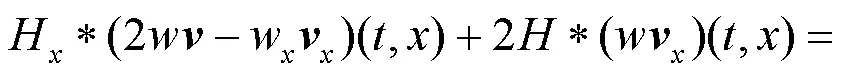
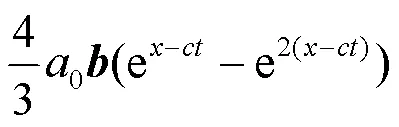
因此, 將式(18)代入式(15), 式(19)代入式(16), 式(20)代入式(17), 并使用式(22)~(27)可以得到式(11). 定理證明完畢.
3 結論

[1] Camassa R, Holm D D. An integrable shallow water equation with peaked solitons[J]. Physical Review Letters, 1993, 71(11):1661-1664.
[2] Escher R, Kohlmann J, Lenells J. The geometry of the two-component Camassa-Holm and Degasperis-Procesi equations[J]. Journal of Geometry and Physics, 2011, 61(2):436-452.
[3] Kouranbaeva S. The Camassa-Holm equation as a geodesic flow on the diffeomorphism group[J]. Journal of Mathematical Physics, 1999, 40(2):857-868.
[4] Gui G, Liu Y, Olver P J, et al. Wave-breaking and peakons for a modified Camassa-Holm equation[J]. Communications in Mathematical Physics, 2013, 319(3):731-759.
[5] Chou K S, Qu C Z. Integrable equations arising from motions of plane curves[J]. Physica D: Nonlinear Phenomena, 2002, 162(1/2):9-33.
[6] Lenells J. Traveling wave solutions of the Camassa-Holm equation[J]. Journal of Differential Equations, 2005, 217(2):393-430.
[7] Sanders J A, Wang J P. Integrable systems in-dimensional Riemannian geometry[J]. Moscow Mathematical Journal, 2003, 3(4):1369-1393.
[8] Spivak M. A Comprehensive Introduction to Differential Geometry[M]. 2nd ed. Wilmington: Publish or Perish Inc., 1979.
[9] Sanders J A, Wang J P. Integrable systems in-dimensional conformal geometry[J]. Journal of Difference Equations and Applications, 2006, 12(10):983- 995.
[10] Chen M, Liu S Q, Zhang Y J. A two-component generalization of the Camassa-Holm equation and its solutions[J]. Letters in Mathematical Physics, 2006, 75(1): 1-15.
[11] Qu C Z, Song J F, Yao R X. Multi-component integrable systems with peaked solitons and invariant curve flows in certain geometries[J]. Symmetry Integrability and Geometry: Methods and Applications, 2013, 9:001.
[12] Kang J, Liu X C, Qu C Z. On an integrable multi-component Camassa-Holm system arising from M?bius geometry[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2021, 477(2251):20210164.
[13] Jenson G R, Musso E, Nicolodi L. Surfaces in Classical Geometries[M]. New York: Springer, 2016.
[14] Sharpe R W. Differential Geometry[M]. New York: Springer, 1997.
A multi-component Camassa-Holm equation arising from M?bius geometry
QIN Hui, WANG Bao*
( School of Mathematics and Statistics, Ningbo University, Ningbo 315211, China )
In this paper, we study curve flows in general M?bius geometry, and prove that a class of multi-component Camassa-Holm equations are equivalent to an invariant curve flow in M?bius geometry, which is a multi-component generalization of the two-component Camassa-Holm equation, and can also be regarded as a dual integrable system of a class of multi-component KdV systems. We also obtain a peaked solution for a degradation case of multi-component Camassa-Holm equations.
invariant curve flow; M?bius geometry; Camassa-Holm equation; multi-component Camassa-Holm system; peaked solution
O29
A
1001-5132(2023)03-0043-07
2022?11?08.
寧波大學學報(理工版)網址: http://journallg.nbu.edu.cn/
覃慧(1996-), 女, 廣西桂平人, 在讀碩士研究生, 主要研究方向: 可積系統. E-mail: qhwbatg@163.com
通信作者:王寶(1990-), 男, 河北保定人, 講師, 主要研究方向: 可積系統. E-mail: wangbao@nbu.edu.cn
(責任編輯 韓 超)

