基于特征提取的電氣設備紅外圖像識別算法

黨曉婧, 劉順桂, 朱光南, 欒孟杰, 沈民強

(1. 中國南方電網(wǎng)有限公司 深圳供電局電力科學研究院, 廣東 深圳 518000; 2. 浙江大立科技股份有限公司 a. 技術服務部, b. 生產(chǎn)部, 杭州 310000; 3. 綏化學院 信息工程學院, 黑龍江 緩化 152061)

輸變電設備是構成電力系統(tǒng)的基礎設備,輸變電設備的安全、穩(wěn)定運行直接影響電力系統(tǒng)的可靠性,因而全面掌握輸變電設備的運行狀態(tài)是保障電力供應的必要條件[1-2].此外,新興技術在電氣設備檢修運維方面的應用具有重要的理論意義和實際價值.

智能巡檢機器人、無人機等先進裝備在電氣設備巡檢過程中的應用,顯著提高了工作效率,降低了巡檢人員的工作強度,緩解了電網(wǎng)規(guī)模日益擴張與人員配置不足之間的矛盾[3-4].但從大量圖像數(shù)據(jù)中獲取有用信息,實現(xiàn)電氣設備的準確識別與故障判斷,成為了當前電力巡檢工作急需解決的問題[5-6].

計算機視覺技術的發(fā)展使得電氣設備的圖像識別與故障診斷技術有了新的突破[7-8].周可慧等[9]針對電氣設備紅外圖像分辨率差、識別度低等問題,采用RGB、HSV顏色空間轉化和SeamCarving縮放處理建立了CNN-Alex網(wǎng)絡,使得設備識別準確率提高到97.7%.朱正國等[10]針對配電網(wǎng)無人化管理的要求,提出了一種BRISK算法與平移因子相結合的圖像識別方法,實現(xiàn)了對配電設備危險情況的準確識別.張從新等[11]利用多種形態(tài)學處理算法,并結合Canny算子實現(xiàn)了復雜背景下的輸電線路設備識別.王啟銀等[12]基于形態(tài)學權重自適應算法研究了變電站電氣設備的圖像分割處理方法,顯著提高了變電站設備紅外圖像的特征提取準確率與識別準確度.江澤濤等[13]提出了一種改進脈沖耦合神經(jīng)網(wǎng)絡的紅外與可見光圖像融合算法,并采用靜態(tài)小波變換融合策略,顯著提升了融合圖像的清晰度及信息熵.

利用人工智能算法實現(xiàn)對電氣設備及其故障的識別與分類始終是國內外研究的重點[14-16].本文針對智能變電站巡檢機器人對變電站設備紅外圖像識別問題,研究了基于矩函數(shù)的特征提取技術在電氣設備紅外圖像識別中的應用.本文從矩函數(shù)的一般定義出發(fā),以數(shù)字圖像的幾何矩為基礎,導出包含圖像特征信息的不變矩,提取圖像特征參數(shù),并利用神經(jīng)網(wǎng)絡分類算法完成了電氣設備的紅外圖像分類識別.

1 基本概念

統(tǒng)計學上,矩表征了隨機變量的分布情況.例如,隨機變量的期望可以定義為一階原點矩,即

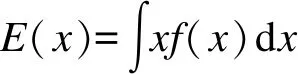
(1)

式中,f(x)為隨機變量的概率密度.隨機變量的方差可以定義為二階中心矩,即

(2)

對于一幅圖像函數(shù)而言,假設像素點(x,y)處的亮度值由像素p(x,y)表示,則其i+j階矩函數(shù)表達式為

(3)

式中:ξ為函數(shù)的定義域,即平面圖像所在的區(qū)域;Ψij(x,y)為定義域內關于(x,y)的連續(xù)函數(shù),又稱矩的權核.

數(shù)字圖像中計算得到的矩集描述了圖像形狀的全局特征,同時包含各種不同類型的幾何特性.因此,可將圖像矩的這種特性描述能力應用于圖像分類與識別.

1.1 幾何矩

幾何矩屬于矩函數(shù)的一種,其核函數(shù)為像素坐標的冪.對于一幅圖像而言,像素點坐標的變換可用矩空間相應的變換進行表達與分析.此外,相比核函數(shù)為復數(shù)的情況,在計算機處理過程中幾何矩更易被執(zhí)行與完成.

定義一幅數(shù)字圖像的i+j階二維幾何矩為mij,即

(4)

圖像的不同階幾何矩表征了圖像不同亮度分布的空間特性,因此,利用幾何矩集來構建圖像的特征集具有良好的理論依據(jù).零階幾何矩表征了一幅圖像的總亮度,若圖像由二值函數(shù)表示,則零階幾何矩表征目標區(qū)域的亮度為

(5)

一階幾何矩有兩個,分別為m10與m01,且分別對應圖像關于x軸和y軸的亮度矩.對于二值圖像而言,矩心(x0,y0)給出了圖像目標區(qū)域的幾何中心,其計算公式為

(6)

通常將參照系的原點移至圖像亮度矩心的幾何矩稱為中心矩,其計算表達式為

(7)

圖像的這一變化,使得矩的計算可以獨立于圖像的參照系.由此,可以利用中心矩導出不受圖像平移、旋轉、縮放影響的特征量,將其應用于圖像識別.

1.2 圖像矩函數(shù)的不變量

根據(jù)矩函數(shù)的定義可知,中心矩本身具有平移不變性.這是由于中心矩是利用圖像的中心為坐標原點進行定義的,而圖像中心不受坐標移動的影響.因此,由幾何矩直接計算得到的二階、三階中心矩也保持平移不變的特性.

對于縮放不變量,假設圖像的像素坐標經(jīng)過相同的尺度縮放因子k變換,則

(8)

dx′dy′=k2dxdy

(9)

尺度變換后圖像幾何矩可由原始圖像的幾何矩進行表示,即

m′ij=ki+j+2mij

(10)

且有

m′00=k2m00

(11)

消去式中的未知尺度因子k得到

(12)

因而可得在圖像的平移與縮放變換下保持不變的φij函數(shù),即

(13)

假設圖像的旋轉角度為θ,則

(14)

變換后的圖像幾何矩為

p(x,y)dx′dy′

(15)

計算可得

(16)

(17)

由式(16)和(17)可知,m20+m02具有旋轉不變性,即

m′20+m′02=m20+m02

(18)

若用φij代替mij,即可得到幾何矩不變量函數(shù).這些函數(shù)均具有旋轉不變性、平移不變性和縮放不變性,因此,可以用于描述圖像的本質特征且不受圖像平移、縮放、旋轉的影響.圖像識別中常用幾何矩不變量表達式為

I1=φ20+φ02

(19)

(20)

I3=(φ30-3φ12)2+(φ03-3φ21)2

(21)

I4=(φ30+φ12)2+(φ03+φ21)2

(22)

(23)

(24)

計算過程中發(fā)現(xiàn)矩不變量I1～I6數(shù)值較小,且變化范圍較大,應用過程中不便計算.為了簡化計算、便于比較,對上述不變矩進行修正,同時消除可能出現(xiàn)的負值,其表達式為

Zi=|lg|Ii|| (i=1,2,…,6)

(25)

Lena圖為圖像處理中使用最廣泛的標準測試圖之一,本文利用該圖來測試修正前后不變矩參數(shù)的變化特征.圖1為本文測試中采用的Lena圖,處理過程中將其轉換為一個450×450的灰度信息矩陣,然后計算其不變矩參數(shù).表1為修正前后Lena圖不變矩的計算值.

表1 Lena圖像不變矩修正前后比較

圖1 Lena圖

由表1可知,修正前不變矩的數(shù)值較小,數(shù)量級差異較大且還可能出現(xiàn)負數(shù).修正后的不變矩值比修正前的值大,數(shù)量級差異較小且不包含負數(shù),因此,具有更強的可比性,便于圖像識別和匹配處理.

2 不變矩的改進

經(jīng)過平移、旋轉、縮放變換的圖像在處理過程中會產(chǎn)生重復采樣和重量化的誤差,導致不變矩的準確性降低.為了消減這種對圖像識別的影響,定義改進后的中心矩表達式為

p(x,y)dxdy

(26)

式中,x″和y″為修正系數(shù)且分別定義為

(27)

修正后用于表征圖像特征的不變矩仍由式(19)～(24)計算得到.

目標圖像p(x,y)經(jīng)(Δx,Δy)平移后的圖像p′(x,y)可表示為

p′(x,y)=p(x-Δx,y-Δy)

(28)

將式(28)代入式(26)可得

p(x-Δx,y-Δy)d(x-Δx)d(y-Δy)

(29)

令zx=x-Δx,zy=y-Δy,式(29)可整理為

p(zx,zy)dzxdzy

(30)

分析可知,式(30)與式(26)是等價的,即原圖像p(x,y)和平移后的圖像p′(x,y)的中心矩相同.

對原圖像p(x,y)進行比例系數(shù)為k的縮放變換,則

(31)

將縮放后的圖像代入式(26),計算得到中心矩,即

kp(x,y)dxdy=ki+j+2μij

(32)

由式(32)可知,縮放前后的歸一化中心矩也是等價的.因此,可以證明改進后的中心矩具有縮放不變性.

3 算法驗證

為了驗證I1～I6不變矩的特征提取效果,選擇變電站設備紅外圖像經(jīng)分割后得到的二值圖像不變矩參數(shù)進行計算.圖2為變電站原始紅外圖片,圖3為對紅外圖像進行分割提取處理后的二值圖像.

圖2 變電站設備紅外圖像

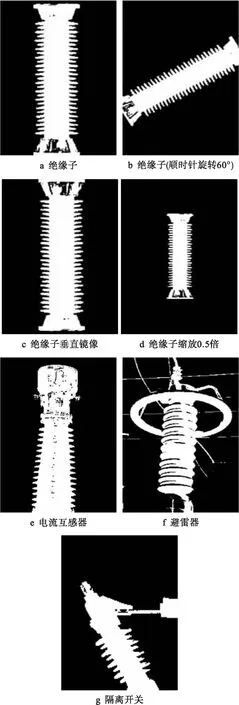
圖3 典型變電站設備二值圖像

采用改進前后的不變矩計算方法,計算圖3b～d不變矩與圖3a不變矩的差異值,結果如圖4所示.由圖4可知,對于同一設備而言,改進后的不變矩數(shù)值優(yōu)于改進前.通過對計算方法的改進能夠降低由于圖像平移、旋轉、縮放造成的計算誤差.

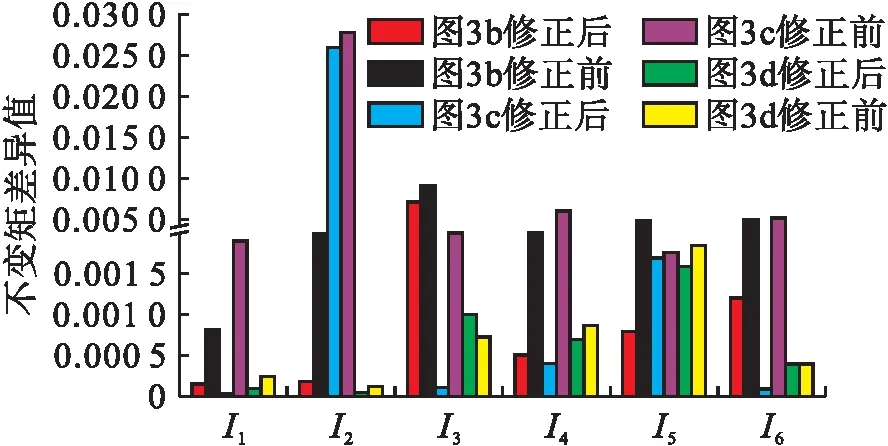
圖4 不變矩改進前后差異值比較

對圖3進行不變矩計算,計算結果如表2所示.對比計算3b～d不變矩與圖3a不變矩的差異值,結果表3所示.由表3可知,不同設備不變矩差異值要明顯大于同一設備的不變矩差異值,不同設備的均值與方差變化較大而同一設備較小,說明不變矩參數(shù)能夠較好地反映不同設備之間的差異,有利于設備識別.同一設備的旋轉變化會造成不變矩差異的擴大,縮放變化對不變矩造成的影響較小,因此,在獲取圖像過程中要盡量減少鏡頭的轉動,保持圖像的穩(wěn)定性.

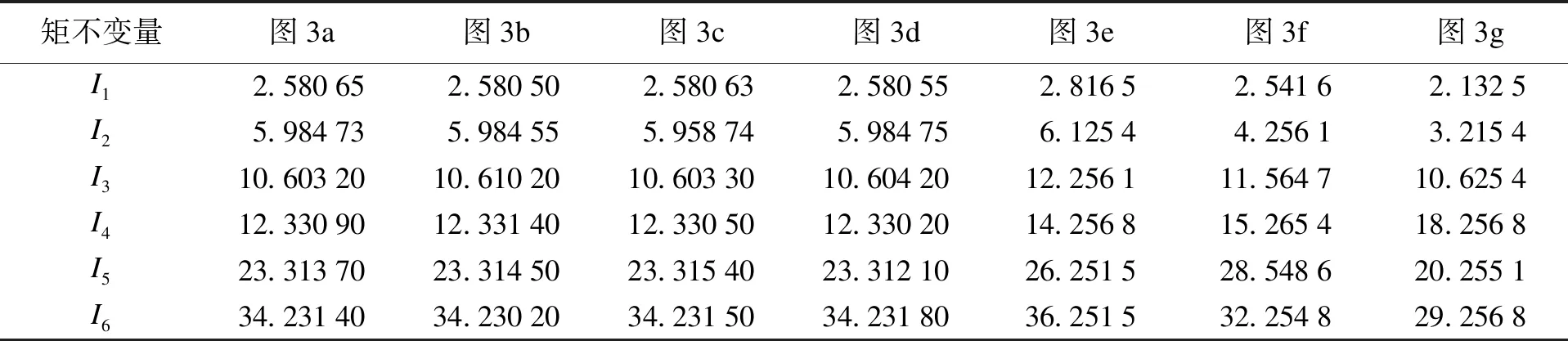
表2 典型設備圖像不變矩陣計算結果

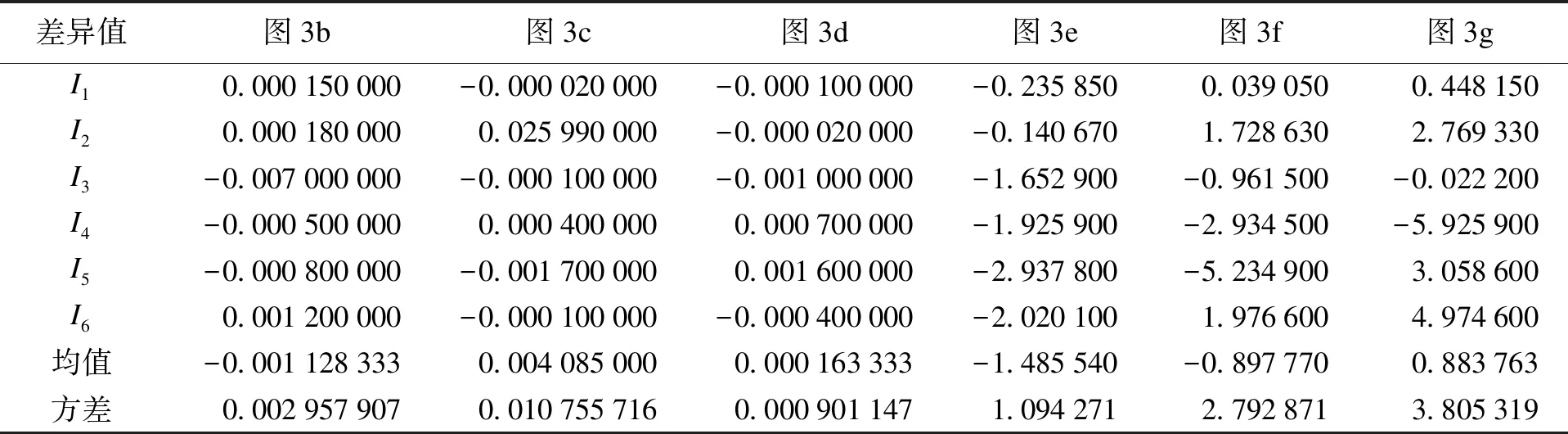
表3 典型設備圖像不變矩差異值比較

選取絕緣子、電流互感器、避雷器、隔離開關4種分割后的變電站典型設備圖像30幅,并對圖像進行順時針旋轉60°、垂直方向鏡像、縮放0.5倍和2倍處理,得到共計600幅圖像并將其作為輸入樣本并進行神經(jīng)網(wǎng)絡訓練.選擇4種典型設備的紅外圖像各50幅進行神經(jīng)網(wǎng)絡分類識別,識別結果如表4所示.由表4可知,利用各類設備紅外圖像的不變矩作為特征提取參數(shù),對其進行識別綜合識別率可達94%,能夠滿足實際應用需求.

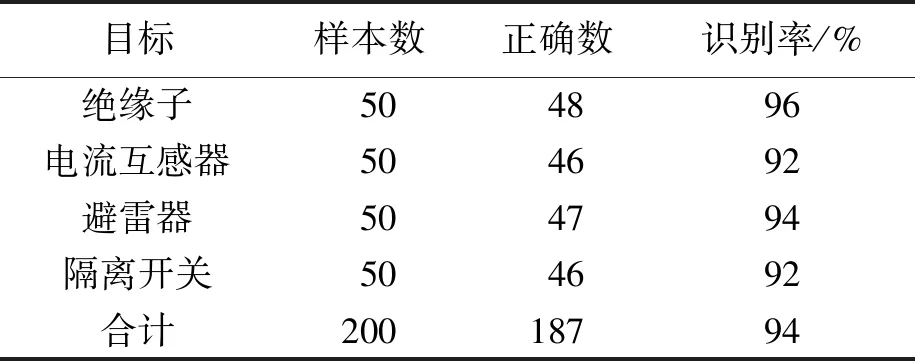
表4 神經(jīng)網(wǎng)絡分類識別結果

4 結 論

本文研究了電氣設備紅外圖像的特征提取方法,從矩函數(shù)的數(shù)學概念出發(fā),建立表示圖像特征的幾何矩,推導矩函數(shù)的平移、縮放、旋轉不變性,得到6個用于圖像識別的幾何矩不變量,得到如下主要結論:

1) 在不變矩的基礎上,設計改進的中心矩計算法可以消除由于圖像變換過程中造成的計算誤差,能夠有效提高不變矩參數(shù)計算的準確性;

2) 采用本文提出的6個不變矩作為電氣設備的紅外圖像特征參數(shù),利用神經(jīng)網(wǎng)絡對圖像進行訓練與識別,其識別準確率可達94%,能夠滿足實際應用需求.