爆裂輪胎精確建模及其動態特性仿真方法研究*

賈雪峰，馮啟章，劉獻棟，單穎春

（北京航空航天大學交通科學與工程學院，北京 100191）

前言

作為汽車與路面唯一接觸的部件，輪胎對車輛的行駛安全至關重要，而輪胎爆裂是汽車的危險故障。爆胎發生后，胎內空氣迅速泄漏，輪胎的力學特性瞬間發生巨大變化，嚴重影響車輛的操縱穩定性，極易引發交通事故。據資料顯示，高速公路由于爆胎引發的交通事故高達32%［1］。

為減輕爆胎帶來的后果，國內外許多學者對爆胎后汽車的動力學性能進行了研究。王英麟等［2］通過試驗對比分析了零胎壓輪胎和正常胎壓輪胎在不同工況下的力學特性，假設爆胎持續時間為0.1 s，將爆胎過程簡化為輪胎徑向剛度、縱滑剛度與側傾剛度等參數在爆胎持續時間內線性變化的過程，由此分析了爆胎后汽車的運動特性。此外，部分學者［3-5］基于類似的假設研究了不同工況下爆胎汽車的動力學響應，并提出了控制策略。但是真實爆胎過程的持續時間與輪胎轉速、裂口尺寸等多種因素相關，爆裂輪胎的剛度特性也在不斷改變，上述簡化和假設存在明顯不合理。因此，需要對爆胎過程進行精細研究，以準確描述在泄氣過程中輪胎力學特性的演變規律和機理。另一方面，現代車輛朝著智能化的方向不斷發展，這對輪胎的狀態監測提出了更嚴格的要求，無人駕駛汽車須精準感知與預測爆胎的發生，進而有效控制車輛運動，這更需要準確的輪胎爆胎信息。同時，研究爆胎過程還有助于輪胎的防爆結構設計，從根本上減少爆胎事故發生。

為此，國內外學者對爆胎過程進行了較為深入的研究。Tseng 等［6］首次仿真模擬了輪胎爆裂壓力、高速自由旋轉和柱塞能量測試的破壞性試驗。Orengo 等［7］采用壓力氣囊的形式為輪胎充氣，然后通過模擬胎圈脫離輪輞實現輪胎泄氣，由此仿真分析了輪胎撞擊路邊危險物引起的爆胎現象。Michel等［8］對載貨汽車輪胎進行了水壓爆破試驗和有限元仿真，發現輪胎的最大應力出現在輪輻對側胎圈的內下角，胎圈鋼絲斷裂導致輪胎爆裂。蔡永周等［9-10］開發了一種用于模擬爆胎的試驗裝置，首先基于輪胎泄氣時間計算爆胎口徑，在輪輞處設置放氣口模擬輪胎泄氣，然后將獲得的胎壓時間歷程作為載荷條件施加于有限元輪胎內壁進行爆胎過程仿真。此外，還有一些學者［11-13］通過識別簾線和胎圈鋼絲在極端載荷下的應力，預測了輪胎的破裂壓力，并分析了輪胎結構對承載能力的影響。但這些研究均未考慮輪胎滾動工況下的爆裂和胎內空氣的流失，無法準確模擬輪胎爆裂過程，進而無法分析爆裂輪胎的瞬態力學特性。

為準確描述爆胎過程，本文中引入考慮輪胎多種橡膠材料、橡膠-簾線復合材料失效特性的精確輪胎模型，提出采用結構化任意拉格朗日-歐拉算法分別模擬輪胎內、外部空氣，僅在胎內空氣與輪胎-車輪總成之間施加流-固耦合的仿真分析方法，并解決其帶來的系列問題。然后，基于該方法對汽車輪胎滾動時撞擊路緣引發的爆胎過程進行仿真分析，得到胎壓和輪胎力學特性的演變規律，并獲得輪胎滾動速度、初始氣壓和裂口尺寸對輪胎爆裂過程的影響機理。同時，為驗證本文仿真模型和方法的正確性，還對理論計算所獲得爆胎過程胎壓變化規律與仿真結果進行對比與分析。

1 輪胎-車輪-空氣的流-固耦合模型

爆胎本質是輪胎發生破裂，胎內壓縮空氣從裂口快速流失的物理現象。準確研究爆胎過程，就要求輪胎模型準確，同時還須考慮輪胎的橡膠材料和橡膠-簾線復合材料的失效特性以及空氣與輪胎-車輪總成的流-固耦合。為研究輪胎爆裂過程這樣一個具有高度非線性的瞬態動力學問題，本文中采用LS-DYNA 軟件建立包含6 種橡膠材料和3 種橡膠-簾線復合材料本構方程及失效特性的輪胎、車輪、空氣的流-固耦合模型，其中采用結構化任意拉格朗日-歐拉算法模擬輪胎內、外部空氣的大變形運動，并通過浸沒邊界法實現胎內空氣與輪胎-車輪總成的流-固耦合，克服了傳統ALE 算法中極易出現的流體穿透結構引發的泄漏問題。

1.1 輪胎-車輪有限元模型

采用一款常用的235/55 R19 乘用車輪胎，輪胎的斷面結構如圖1 所示，共包含9 種橡膠材料和3 種簾線材料，以準確模擬輪胎的真實特性。其中，橡膠基體主要包含胎面膠、胎側膠、三角膠、耐磨膠、帶束膠等部分；簾線部分包含帶束層簾線、胎體簾線和冠帶層簾線，并采用橡膠-簾線復合材料模擬其材料屬性。

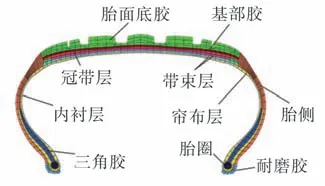
圖1 輪胎的二維截面

為保證輪胎的網格質量和顯式計算的準確性，輪胎的二維截面模型全部劃分為四邊形單元。通過二維截面繞中心軸線旋轉，得到全為六面體單元的三維輪胎有限元模型，車輪-輪胎總成的三維有限元模型如圖2所示。

圖2 車輪-輪胎總成的三維有限元模型

1.2 材料模型及失效準則

1.2.1 橡膠材料

在輪胎的主體結構部分，胎面、胎側、胎圈、三角膠、內襯層等區域采用了不同硬度的超彈性橡膠材料，本文中采用了一種基于應力-應變曲線的簡化橡膠材料（SRM）本構模型［14-15］，該橡膠模型在Ogden超彈性公式的基礎上進行改進，考慮了材料的動態效應，由不同應變率下工程應力和工程應變的單軸載荷曲線族描述，可實現輪胎模型通用于準靜態和瞬態等各種工況。

本文采用的胎面底膠、基部膠、胎側膠、三角膠、內襯層等橡膠材料的應力-應變曲線分別如圖3～圖7所示［16］。

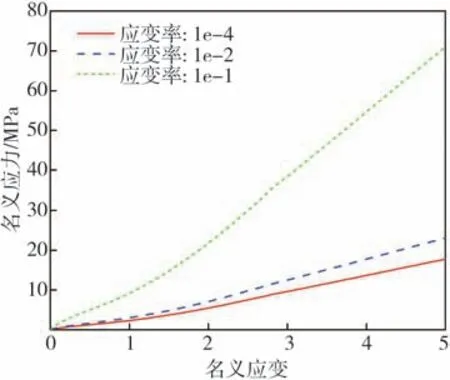
圖3 胎面底膠的應力-應變曲線

圖4 基部膠的應力-應變曲線

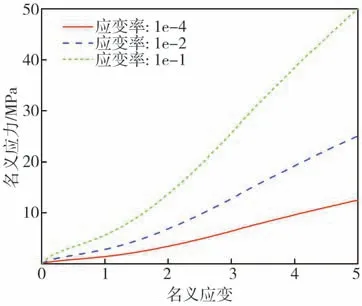
圖5 胎側膠的應力-應變曲線

圖6 三角膠的應力-應變曲線

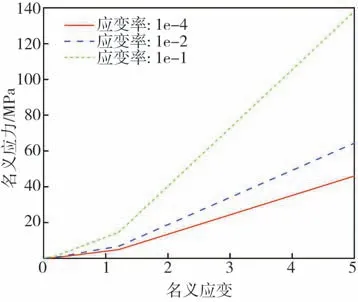
圖7 內襯層的應力-應變曲線

橡膠材料SRM本構方程采用的Ogden公式為

式中：W為應變能為偏伸長率為相對體積比為伸長率；μj、αj為材料參數；K為材料的體積模量。

橡膠材料采用聚合物失效表面［17］的失效準則，該準則假設橡膠在應變能密度達到一定值時發生失效，并由有限彈性應變張量不變量來表示，其表達

式中：I1和I2為第1、2階應變張量不變量；Γ1、Γ2和K是失效表面的控制參數，由單軸拉伸試驗和不同拉伸比的雙軸拉伸試驗等確定。本文采用的聚合物失效表面參數如圖8 所示，當橡膠的應變狀態處在曲線之外時，單元即發生失效。

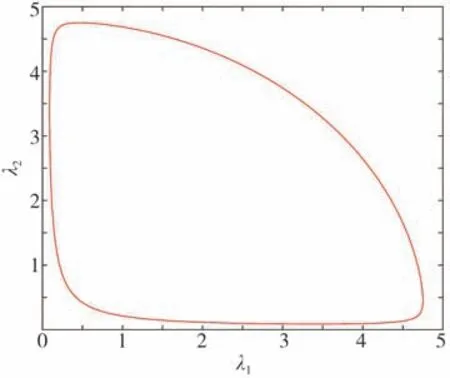
圖8 聚合物失效表面

1.2.2 橡膠-簾線復合材料

冠帶層、帶束層和胎體簾布層是輪胎的主要承載結構，內部簾線方向一致，具有橫觀各向同性。因此本文中的橡膠-簾線復合材料采用橫觀各向同性材料描述，力學性能根據組分的性能來預測，并選取Halpin-Tsai 公式［18］確定其材料參數。橡膠-簾線復合材料的材料參數選自文獻［9］，具體數值如表1所示。

表1 橡膠-簾線復合材料的材料參數

橡膠簾線復合材料的失效模型采用美國航空航天局Lewis研究中心［19］提出的經驗預測公式：

式中：XT和XC分別為橡膠-簾線復合材料的軸向拉伸和壓縮強度；TC和CC分別為單根簾線的軸向拉伸和壓縮強度；VC為簾線在復合材料中的體積分數。

由于簾線的彈性模量遠大于橡膠，橡膠-簾線復合材料的最大主應力方向接近于簾線的軸向，因此選取復合材料失效時的最大主應力為軸向抗拉強度，具體數值如表2所示。

表2 橡膠-簾線復合材料失效時的最大主應力

1.3 空氣與輪胎-車輪總成的流-固耦合

任意拉格朗日歐拉（ALE）算法適用于模擬空氣的大變形力學響應，并可實現結構與流體的相互耦合。但輪胎內部的壓縮空氣與輪胎-車輪總成耦合時，由于輪胎內表面附近空氣單元的不規則，傳統的ALE 算法極易出現流-固耦合中流體穿透結構引發的泄漏問題。而結構化任意拉格朗日-歐拉算法（S-ALE）可利用網格的邏輯性和規律性，解決這一問題。因此，本文采用S-ALE 算法分析空氣的響應，并提出輪胎內、外部的空氣采用兩種不同壓強的多物質材料模擬，但僅在胎內空氣與輪胎-車輪總成之間施加流-固耦合。

1.3.1 空氣的本構方程和狀態方程

空氣的變形較大，須同時使用本構方程和狀態方程才能精確模擬空氣的大變形行為。其中，空氣的本構方程用來計算總應力的應力偏量，狀態方程則用來計算平均應力：

式中：σij為應力張量；為應力偏量；P為平均應力，P=-σkk/3。

空氣采用如下黏性本構方程：

式中：vd為動力黏度為偏應變率。

空氣的狀態方程采用理想氣體物態方程的形式，通過計算壓強和密度之間的關系確定空氣的變形行為。由于汽車輪胎爆裂后，胎內空氣迅速泄漏會引起胎外空氣分布的變化，胎外空氣對爆胎過程具有一定程度的影響，因此本文同時考慮輪胎內外部氣壓，以保證與實際情況相符。本文模擬輪胎的相對大氣壓為0.253 MPa，由于標準大氣壓為0.101 MPa，則輪胎內部壓縮空氣的絕對大氣壓為0.354 MPa。輪胎內、外部空氣具有不同的壓強，對應采用不同的狀態方程。

1.3.2 結構化任意拉格朗日-歐拉算法

本文中應用一種新的結構化任意拉格朗日-歐拉（S-ALE）算法［20］。與傳統ALE 算法不同，S-ALE算法采用正交結構化網格解決ALE 問題，單獨對網格和多物質材料建模，然后在初始階段和每一個時間步長計算完成后，將多物質材料填充在立方體網格內。在本文的模擬中，輪胎滾動時，無須在每一時間步長上實時更新網格，能更精確地捕捉空氣位置。同時，它對流-固耦合中的泄漏具有穩健的控制能力，并能更準確地預測空氣對輪胎內表面的壓力載荷峰值，提高流-固耦合的穩定性，而不會出現ALE算法中的泄漏問題。

S-ALE 算法的實現可分為兩個階段，分別為拉格朗日時間步和對流時間步。在拉格朗日時間步內，網格隨物質一起運動，這個階段通過求解3 個控制方程和材料的狀態方程，確定密度、節點速度、壓強和內能等狀態量；在對流的時間步內，對穿過單元邊界的質量、動量和內能進行計算，將物質映射到重新劃分的網格內。

1.3.3 流-固耦合和邊界條件

輪胎-車輪總成采用Lagrangian 算法，輪胎內、外部的空氣單元采用S-ALE 算法，僅需在胎內壓縮空氣與輪胎-車輪總成之間定義流-固耦合，胎內空氣會對輪胎-車輪總成施加壓力載荷，而輪胎-車輪總成相當于胎內空氣的邊界條件，約束其運動。

在S-ALE 算法中，流-固耦合的界面處理采用浸沒邊界法［21］，該方法使用Euler變量描述流體的狀態，使用Lagrangian 變量描述結構的邊界，并通過光滑化的δ近似函數分布節點力和插值流體質點的速度來實現流體和結構的相互作用。流體受到結構對其彈性邊界產生的作用力稱為力源，浸入邊界的力源分布表示為

式中：f(s，t)表示浸入邊界產生的單位力；s為歐拉網格節點的位移；δ為光滑化的Dirac delta 近似函數；X為拉格朗日網格節點的位移；x為邊界曲線的坐標。

為考慮輪胎在安裝過程中的過盈裝配，本文通過輪胎充氣的方式實現胎圈與輪輞間的過盈接觸，但仿真過程中輪胎內部的空氣ALE 單元無法識別此接觸，仍會從接觸面之間流出，因此本文在胎圈和輪輞之間采用一層氣囊織物，以形成密封空間?？椢锊捎煤穸葹?.3 mm 的膜單元模擬，并與輪胎耐磨膠實體單元的節點合并。此外，輪胎外部的空氣域施加無反射邊界條件，用來模擬無限的空氣，一方面可防止邊界產生的反射波與結構發生耦合作用，另一方面還可減少空氣域的體積，降低計算成本。

2 爆胎過程的仿真與分析

為準確模擬輪胎的真實運動，需要依次對輪胎充氣和施加徑向載荷，并使輪胎作純滾動。但在上述工況仿真時，由于胎內空氣與輪胎-車輪總成采用流-固耦合算法，會產生輪胎應力波動、胎圈處空氣泄漏和胎壓計算異常等問題，本節將解決上述問題，并模擬輪胎撞擊路緣引發的爆胎過程，揭示輪胎爆裂過程瞬態特性的變化規律，最后通過對比分析仿真與理論計算的胎壓變化，驗證仿真模型的正確性。

2.1 輪胎載荷的施加

輪胎充氣是通過在輪胎內、外部填充不同壓強的空氣實現的，胎壓由空氣的壓差產生。但在填充完成的瞬間，胎內空氣會對輪胎內表面施加很大的壓力載荷，導致輪胎結構的應力與變形劇烈振蕩，難以平衡，與實際充氣過程不符。因此，本文首先對輪胎內表面施加反向的均布載荷與該壓力平衡，然后將載荷值逐漸減小至0，以反向卸載的形式實現輪胎充氣。

輪胎徑向載荷的施加分為兩個步驟，首先固定輪輞，對路面施加豎直向上的強制位移，同時約束其他方向的自由度。待載荷穩定后，將路面完全固定，車輪中心點與剛性輪輞耦合，在耦合點處施加豎直向下的集中載荷，同時釋放車輪垂直方向的自由度。載荷值取1/4車重，即5 kN。

本文模擬輪胎滾動速度為30 km/h的工況，為保證輪胎純滾動，對車輪和輪胎施加繞輪心的旋轉角速度，對路面施加相反方向的水平初速度，并滿足輪胎接地點的速度大小與路面相同。在輪胎轉動的過程中，由于胎內空氣隨著輪胎一起轉動，空氣的離心力會使胎壓增加，增加量可由式（8）近似計算。

式中：F為空氣的離心力；ρ和V分別為胎內空氣的密度和體積；S為輪胎內表面積；v和R分別為輪胎的轉動速度和轉動半徑。

通過上式計算，空氣的離心力導致的胎壓增加量約為40.8 Pa，遠遠低于標準大氣壓，因此空氣離心力對胎壓影響很小。而在模擬輪胎滾動時，由于流-固耦合算法中輪胎結構浸沒空氣單元的距離隨著轉速的增加而增大，導致胎壓隨著時間的積累持續升高，如圖9 中的紅色虛線所示，這與實際不符，因此須對輪胎滾動工況的胎壓進行修正。

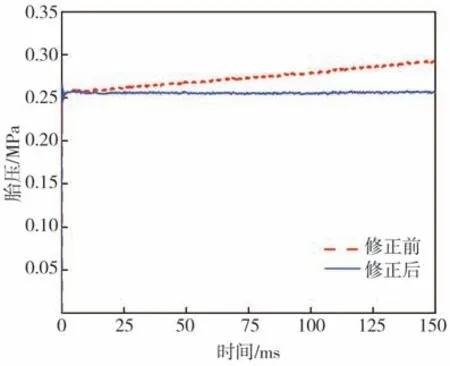
圖9 修正前后的胎壓變化曲線

輪胎滾動過程中胎壓計算值的增加量主要與輪胎轉速和胎內的空氣含量相關，因此必須考慮空氣泄漏對爆胎過程胎壓變化的影響。根據單位時間內胎壓仿真結果的增長量與輪胎轉速和胎內剩余氣體含量成正比，輪胎滾動過程的胎壓變化可由式（9）修正。

式中：p為當前時刻胎壓的仿真值，p1為前一時刻的胎壓值，則p-p1為單位時間內輪胎滾動導致的胎壓增長量為輪胎內部剩余氣體含量占初始含量的百分比，近似為輪胎當前時刻氣壓與初始胎壓的比值。

基于上式對輪胎滾動過程中每一時刻的胎壓值進行修正，修正后的胎壓變化曲線如圖9 中的藍色實線所示。

輪胎爆裂的部分原因是由于撞擊路面的尖銳物體，本文模擬比較常見的輪胎撞擊路緣引發的爆胎，爆裂口徑約為87 mm×34 mm，輪胎爆裂和其內部空氣流失的過程如圖10和圖11所示。

圖10 輪胎的爆裂過程

圖11 輪胎的泄氣過程

2.2 仿真結果與分析

輪胎撞擊路緣后，由于胎側和簾布層的部分單元強度達到材料的失效準則，單元失效刪除而形成裂口，胎內空氣迅速流失，輪胎逐漸變癟。由于裂口空氣流失會導致胎內的氣壓不均衡，裂口處的胎壓相對較小，為便于分析，本文中的胎壓取為氣體對輪胎內壁的平均壓力。若將輪胎開始泄氣的時刻設為0，則在爆胎過程中，輪胎泄氣后的狀態、胎壓變化、泄氣速度和路面對輪胎的徑向力變化分別如圖12～圖15所示。

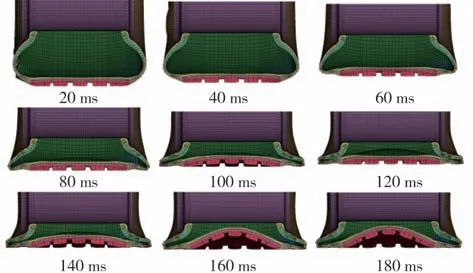
圖12 輪胎泄氣后的狀態變化圖

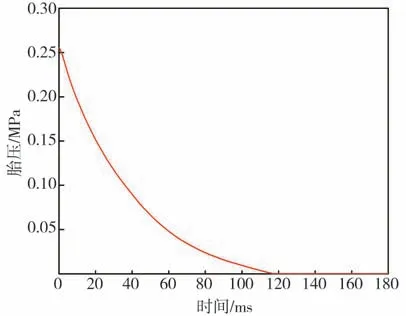
圖13 輪胎氣壓的變化

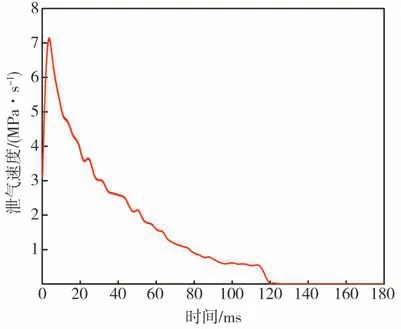
圖14 輪胎泄氣速度的變化

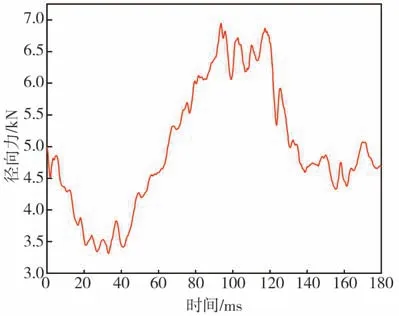
圖15 路面對輪胎的徑向力變化

從圖12可觀察到：輪胎爆裂后的前40 ms內，輪胎的變形較小，輪輞下沉量也較??；40 ms后，胎側部位發生折彎，輪胎內表面逐漸接觸；到達120 ms 時，輪胎內表面完全接觸，隨后發生分離，輪胎和輪輞向上反彈，并帶動部分胎面脫離路面。具體原因可由圖15 來說明，輪胎發生爆裂后，胎內空氣泄漏導致輪胎的徑向剛度降低，承載能力下降，從而路面對輪胎的徑向力減小，進而輪輞處施加的垂向力大于路面的徑向力，輪輞下沉，輪胎滾動半徑不斷減小；而在40 ms 后，胎側逐漸折彎，輪胎承受徑向載荷的能力增強，路面對輪胎的徑向力呈現增大的趨勢，并在95 ms附近達到最大值，載荷峰值約為輪胎正常載荷的1.4 倍；在120 ms 以后，輪胎內表面完全貼合，由于此時路面對輪胎的徑向力大于車輪處施加的垂向力，輪胎向上反彈，輪胎的徑向力減小至5 kN附近，此后輪胎徑向力的波動幅度明顯較小，滾動過程相對平穩。

從圖13 可看出，爆裂輪胎的氣壓持續減小，泄氣持續時間約為116 ms；再由圖14 可看出，輪胎的泄氣速度在4 ms 內迅速增加到最大值，最大泄氣速度可達7.15 MPa/s，然后逐漸減小，在90 ms后，輪胎的泄氣速度降低至0.75 MPa/s，并趨于穩定，直至胎內空氣完全泄漏。這主要由于輪胎開始泄氣后，裂口在4 ms 內擴張至最大尺寸，輪胎泄氣速度顯著增大，隨后裂口尺寸保持不變，但輪胎泄氣使得輪胎內外部空氣壓差減小，導致泄氣速度減慢。最后時刻輪胎的泄氣速度趨于穩定，是輪胎滾動和徑向載荷所致。

而當汽車發生爆胎后，爆裂輪胎的徑向剛度減小會使路面對輪胎的徑向載荷重新分配。為了分析徑向載荷改變對爆裂輪胎特性的影響，本文分別模擬徑向載荷為3 和5 kN 的爆胎工況，如圖16 所示。結果表明，輪胎承受的徑向載荷對爆胎泄氣時間的影響較小，因此本文在輪輞中心的耦合點處施加大小為5 kN 的恒定載荷，不會對泄氣速度和胎壓變化過程造成影響。

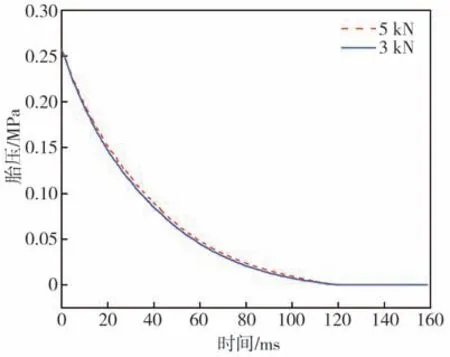
圖16 不同徑向載荷下輪胎氣壓的變化

2.3 爆胎過程仿真模型驗證

為了說明仿真模型的正確性，本文對爆胎過程中胎壓變化進行理論計算，并與仿真結果進行對比分析。輪胎發生爆裂后，胎內外空氣的壓差會使空氣迅速泄漏，若將空氣等效為理想氣體，并認為爆胎過程中的氣體流動滿足伯努利方程，則有以下關系：

式中：p和pa分別為輪胎內部和裂口空氣的壓強；v為輪胎內部空氣的流動速度，假設其數值與輪胎的滾動速度相同；va為輪胎裂口處空氣泄漏的速度；ρ和ρa分別為輪胎內部和外部空氣的密度。則在一定時間間隔內，輪胎內部泄漏的空氣物質的量為

式中：s為輪胎裂口的截面積（由裂口尺寸為87 mm×34 mm得出）；M為空氣的摩爾質量，取為28.963 4 g/mol。此時，胎內的壓強變化可由氣體狀態方程得出：

由此，可依次計算出輪胎泄氣過程的胎壓變化情況。通過計算輪胎滾動速度為30 km/h、輪胎內部空氣總體積為0.038 62 m3的工況，可得到胎壓變化曲線并與爆胎過程的仿真結果進行對比，如圖17所示。

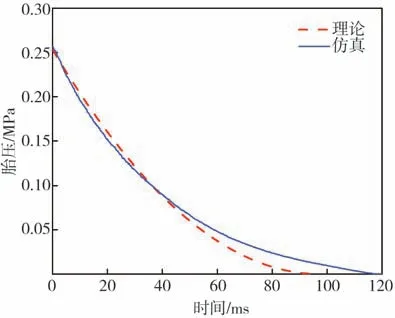
圖17 理論與仿真的胎壓變化對比

顯然，從圖17 可看出，仿真結果是與理論結果誤差較小，在總體上顯示了良好的一致性。在爆胎后的初始階段，胎壓變化的仿真結果與理論值相差很小，兩者產生誤差的主要原因是理論計算中的輪胎內部空氣總體積和爆胎口徑為估計值，與仿真計算值略有區別；在40 ms 以后，理論計算的胎壓變化速度略大于仿真結果，主要由于輪胎爆裂后，裂口處的空氣流失導致胎內空氣分布不均勻，輪胎裂口附近的空氣壓強低于胎內的其他區域，造成輪胎裂口處空氣泄漏的速度va計算值偏大。同時，胎內空氣密度的變化也對結果有一定影響?？傮w來看，本文所提出爆胎過程仿真方法是可行的。

另一方面，通過對比輪胎爆裂后的變形圖和已有文獻［10］中爆胎的試驗結果，也可驗證本文的仿真模型，如圖18 所示。爆胎模擬裝置［10］是在輪輞處設置放氣口，采用電磁閥控制放氣的初始時刻來實現輪胎的泄氣過程。輪胎爆裂后，會出現輪胎內表面互相接觸、輪胎與路面之間接觸面積明顯增大的變形，與本文的仿真結果基本一致，可從另一方面說明本文仿真方法的有效性。

圖18 輪胎爆裂變形圖與爆胎模擬裝置結果圖

3 爆胎過程的主要影響因素分析

影響輪胎爆裂過程的因素較多，主要包括速度、胎壓、溫度、裂口尺寸和運行工況等。本節將研究輪胎滾動速度、胎壓和裂口尺寸對爆胎過程的影響機理。

3.1 輪胎滾動速度對爆胎過程的影響

為研究輪胎的滾動速度對爆胎過程的影響，假設輪胎撞擊路緣后產生的裂口尺寸和位置不變。裂口均為90 mm×38 mm，然后依此改變輪胎的滾動速度為30、60、90 和120 km/h 進行爆胎過程仿真。輪胎爆裂后，胎壓、泄氣速度和路面對輪胎的徑向力變化分別如圖19～圖21所示。

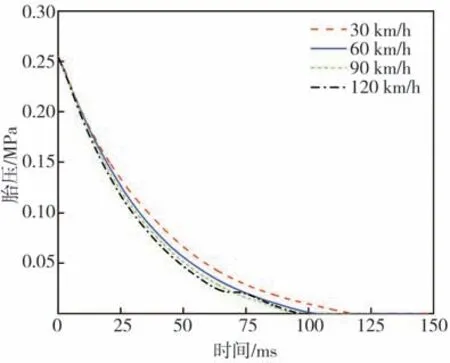
圖19 不同速度下的胎壓變化

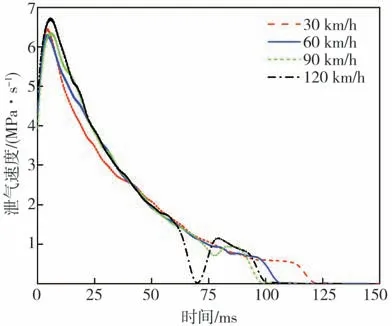
圖20 不同速度下的泄氣速度變化

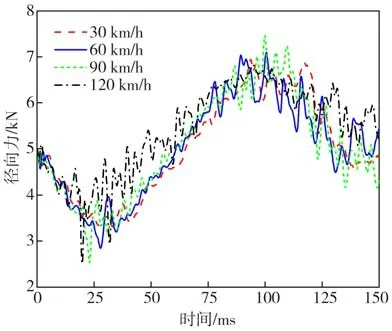
圖21 不同速度下的徑向力變化

從圖19 可看出，隨著輪胎速度增加，爆裂輪胎泄氣時間不斷縮短，原因主要在于爆裂輪胎的泄氣速度隨輪胎的轉速增加而增大，如圖20 所示。輪胎速度為30 km/h 時的泄氣速度明顯低于其他速度工況，因此泄氣時間最長；而當速度超過60 km/h時，泄氣時間縮短不再明顯，反而出現速度為90 km/h時的爆胎泄氣時間略短于輪胎速度為120 km/h的工況的現象，其主要原因是輪胎速度為120 km/h時，胎壓在70 ms 附近幾乎未改變，輪胎泄氣速度減小至0，此時輪胎的裂口靠近路面，裂口處的輪胎內壁互相接觸，阻礙胎內空氣的泄漏。

從圖21 可觀察到，輪胎的滾動速度對爆裂輪胎徑向力的變化趨勢基本沒有影響，但是會影響徑向載荷的峰值與波動頻率。在輪胎徑向力減小的階段，隨著輪胎速度的增加，路面對輪胎徑向載荷的波動幅值和頻率增大，且徑向載荷在更短的時間內達最小值，這是因為速度的提高加劇了輪胎滾動的不穩定；當胎側逐漸折彎后，輪胎的徑向力開始增大，且載荷的波動值先減小后增大；約80 ms 后，輪胎滾動速度為90和120 km/h時，輪胎的徑向力波動較30和60 km/h 小，是由于輪胎轉速高，其內部大部分氣體已泄漏，而輪胎滾動速度為60 km/h 的工況下，輪胎徑向力波動明顯大于30 km/h，說明泄氣的最后階段，徑向載荷受輪胎內部剩余氣體含量和轉速的共同影響；最終幾種工況下輪胎的徑向力均降低至5 kN 附近，輪胎受力趨于穩定。

3.2 胎壓對爆胎過程的影響

環境溫度、車速和徑向載荷等原因均會引起胎壓變化，為研究輪胎初始氣壓對爆胎過程的影響，首先保證在不同胎壓下輪胎所受的徑向力和輪胎的裂口尺寸相同，然后再分別仿真輪胎初始相對壓強為0.222、0.253 和0.283 MPa 下的爆胎過程。在輪胎爆裂后，胎壓、泄氣速度和路面對輪胎的徑向力變化分別如圖22～圖24所示。

圖22 不同初始氣壓下的胎壓變化

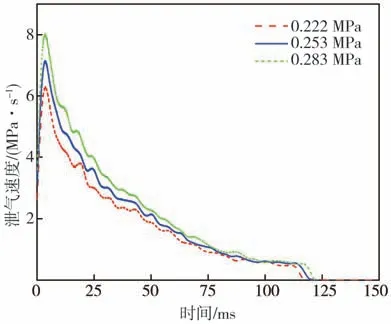
圖23 不同初始氣壓下的泄氣速度變化

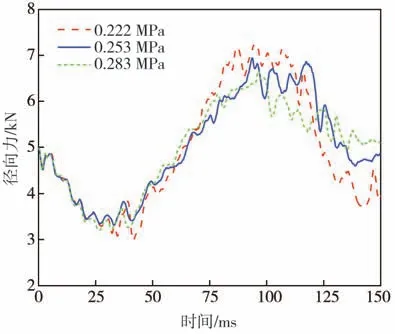
圖24 不同初始氣壓下的徑向力變化

從圖22 可看出，隨著輪胎初始氣壓的增加，爆裂輪胎泄氣持續時間僅從117 增至122 ms，變化并不明顯，主要原因在于當初始胎壓增大時，輪胎內外部空氣壓差增加，致使輪胎爆裂后50 ms 內泄氣速度明顯增大，峰值由6.3 增至8 MPa/s（見圖23），從而使胎內大部分空氣在此階段泄漏。在80 ms后，幾種胎壓下的輪胎泄氣速度均降至0.6 MPa/s左右，并趨于穩定，直至胎內空氣完全泄漏，因此初始胎壓對泄氣持續時間影響較小。

從圖24 可觀察到，胎壓并不會影響爆裂輪胎所受徑向力的變化趨勢，但會影響徑向載荷的波動幅值。當輪胎初始氣壓較低時，路面對輪胎的徑向力波動幅值略大，主要由于輪胎的氣壓低導致其徑向剛度減小，承載能力降低。

3.3 裂口尺寸爆胎過程的影響

輪胎爆裂會產生不同大小的裂口，這對爆胎過程的輪胎特性有著較大的影響。本節為研究裂口尺寸對爆胎過程的影響，依此改變輪胎爆裂后的裂口尺寸為97 mm×39 mm、87 mm×34 mm 和78 mm×30 mm，爆胎后輪胎氣壓、泄氣速度和路面對輪胎的徑向力變化分別如圖25～圖27所示。

圖25 不同裂口尺寸下的胎壓變化

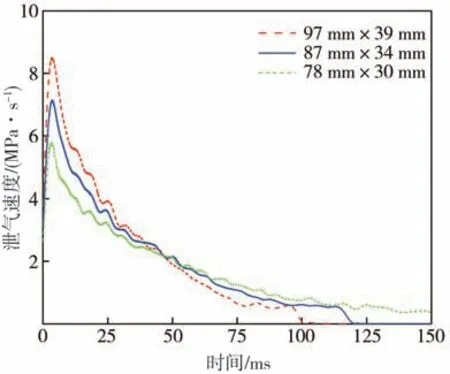
圖26 不同裂口尺寸下的泄氣速度變化

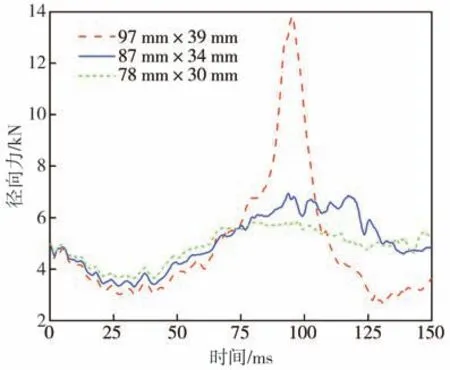
圖27 不同裂口尺寸下的徑向力變化

從圖25 可看出，裂口尺寸增大時，泄氣時間明顯縮短。爆裂輪胎的泄氣速度受裂口尺寸和輪胎內部剩余氣體含量的共同影響，如圖26 所示，在爆胎后的45 ms 內，泄氣速度隨裂口尺寸的增加而增大；而在45 ms 后，反而是裂口尺寸較小的工況泄氣速度較快，這是由于其胎內空氣剩余量較多，輪胎內外部空氣壓差較大。

從圖27 可觀察到，輪胎裂口尺寸對徑向載荷的波動幅值影響較大。當裂口尺寸為78 mm×30 mm時，路面對輪胎徑向力的變化較為平穩，載荷的波動范圍在3.65～5.85 kN 之間；在裂口尺寸為87 mm×34 mm 的工況下，輪胎徑向力的波動有較小程度增加；而當裂口尺寸擴大至97 mm×39 mm 時，輪胎所受的徑向力波動明顯加劇，峰值載荷能夠達到13.85 kN，約為正常載荷的2.8 倍，并衰減較慢。由此可看出，輪胎裂口尺寸較小時，輪胎的運行狀況較為穩定；而當裂口尺寸增大到一定程度后，路面會對輪胎產生很大的沖擊力，工況惡劣程度加劇。

4 結論

為揭示汽車輪胎爆裂過程中動態特性的演變規律，本文中提出了一種可精確描述輪胎爆裂過程的仿真分析方法，并利用該方法仿真了輪胎滾動時撞擊路緣導致胎側破裂而引發的爆胎過程，得出如下結論。

（1）輪胎爆裂的初期，因胎內空氣泄漏導致其徑向剛度迅速降低、承載能力快速下降，導致路面對輪胎的徑向力和輪胎的滾動半徑明顯減小；隨著胎側折彎和輪胎內表面逐漸接觸，輪胎承受徑向載荷的能力逐步增強，路面對輪胎的徑向力呈現增大的趨勢；當輪胎內表面完全貼合后，因路面對輪胎的徑向力大于車輪處施加的垂向力，致使輪胎和輪輞會向上反彈，并帶動部分胎面脫離路面；最后，路面對輪胎的徑向力大小會逐漸降低，直至與輪輞處施加的垂向載荷相等，并在附近波動。

（2）爆裂輪胎的泄氣持續時間短暫，一般在百毫秒級，例如當裂口尺寸為87 mm×34 mm 時，泄氣時間僅持續116 ms；爆裂輪胎的泄氣速度的變化規律是，在短時間內迅速增加之后再逐漸減??；輪胎爆裂后，裂口會迅速擴大，泄氣速度增至最大值，然后隨著胎內空氣的快速流失，胎內外空氣壓差減小，泄氣速度逐漸減慢，并趨于穩定值，直至胎內空氣完全泄漏。

（3）在影響爆胎過程的因素中，輪胎的滾動速度增加，爆裂輪胎的泄氣速度也隨之增大；同時，輪胎的滾動速度會影響徑向載荷的峰值和波動頻率，速度增加會使輪胎滾動的不穩定性增大；初始胎壓對爆裂輪胎所受徑向力的變化趨勢影響不明顯；裂口尺寸增加會使輪胎所受徑向力的波動劇增，顯著加劇輪胎滾動的不穩定性。

本文提出的爆胎過程仿真方法，考慮了輪胎內6 種橡膠材料、3 種橡膠-簾線復合材料的失效特性和胎內空氣與輪胎-車輪總成的流-固耦合，克服了傳統ALE 算法仿真中極易出現的流體穿透結構引發的泄漏問題，解決了輪胎施加載荷時產生的應力波動、胎圈處空氣泄漏和胎壓計算異常等問題，可實現各種工況下的輪胎爆裂精確仿真。同時，該方法能具體分析胎壓和路面對輪胎徑向力的變化情況，更準確地判斷輪胎的受力狀態，對輪胎爆裂的瞬態力學特性研究和汽車爆胎后的動力學分析具有一定意義，并有助于智能汽車對爆胎的快速感知與預測。此外，本文的爆胎仿真方法還可為輪胎結構的防爆設計提供一定參考。

爆胎是一個極為復雜的瞬態過程，后續會搭建爆胎實驗臺對本文的仿真方法及計算結果進行實驗驗證。