精密水浴恒溫系統的建模及控制

楊學義，魯元昊，李思超，胡坤，艾學忠

（吉林化工學院 信息與控制工程學院，微機測控裝置與系統研究室，吉林吉林，132000）

水浴鍋、電熱套筒加熱等是普遍的控溫裝置，尤其水浴鍋，在化學是實驗室、化工生產過程中應用十分廣泛，其控制對象精確程度將會影響工業產品的質量，怎樣使控制對象快速達到預期狀態，是我們研究的重點。針對溫度控制的精度和魯棒性研究問題，國內外學者展開大量研究。文獻[1]采用Delta V 控制算法對加熱爐進行控制，雖然操作簡單，但是控制精度不太理想。文獻[2]采用改進蟻群算法來確定PID 的最優值，但是系統在加熱過程中加熱對象達到期望溫度時間較長，且系統實時性不夠好。文獻[3]采用改進粒子群算法控制加熱爐，控制效果不錯，但是該算法容易陷入局部最優，使迭代出來的參數不是最優，文獻[4]采用PI 自整定參數調節控制系統的溫度，該方法大多依賴于工程師的經驗，該算法僅對于某種特定的控制系統有效，文獻[5] 增量式 PID 控制器控制發動機的溫度，該方法在最佳性能下對應的溫度不是定值，存在一定的差異；文獻[6]采用基于模糊PID 減小了爐溫波動，通過Simulink 仿真來模擬實際溫度，目前仍存在被控對象數學模型與實際存在偏差，文獻[7]提出了粒子群優化串級PID 來控制水浴鍋的溫度，可以快速、穩定控制溫度，但是串級控制過程對每個鍋溫度控制比較復雜。文獻[8]采用Smith-模糊PID 控制器用于橡膠擠出機料筒溫度控制，Smith 預估控制可以提前補償溫度滯后現象，文獻[9]提出了一種全階狀態觀測器來控制加熱爐溫度，上述論文提供了極大的參考價值。

為解決仿真中建立的數學模型對水浴鍋加熱中非線性模型存在誤差，提出了在仿真軟件中建立物理模型，來實現溫度在水浴鍋中溫度傳遞，通過Fuzzy-RBF 神經網絡PID算法，將具有自我學習的智能算法和模糊PID 控制器有機結合起來，來控制水浴鍋的溫度，以此達到克服控制過程中的非線性，增強系統的魯棒性，提高系統控制質量，降低了外界變化給系統造成不良影。

1 介質加熱裝置物理模型

水浴鍋加熱裝置主要由控制箱、加熱絲、磁力攪拌器、溫度傳感器、外鍋以及內鍋組成。由于水浴鍋在控制溫度過程中不僅受到外界溫度的影響，還受其自身鍋體體積和材料的影響，推理出擬合度高的數學模型非比較困難。因此，本文提出在仿真軟件中建立水浴鍋傳熱系統物理模型，解決了數學建模困難問題，更貼近于實際情況。

物理模型搭建見圖1 所示，通過穩定加熱源給系統熱量，熱量通過熱傳遞給外鍋內的水，水加熱的過程中向兩個方向進行熱傳導，一個方向是傳遞給外鍋的鋁層，另一個方向傳遞給內鍋的燒杯，最終熱量傳遞給燒杯的水，以此達到溫度控制。經實驗可知，給定溫度信號通過接入PWM 模塊產生脈寬調制信號，信號再經過控制熱流率源產生熱量，熱量經過傳導熱模塊傳遞給熱質量塊，在經過可導熱的管道，使外鍋內的水升溫，鍋內的水通過一個壓力泵實現內循環，外鍋專門有一個導熱口，通過這個口使外鍋的溫度傳遞給內鍋，內鍋與外鍋模型基本一致，在導熱口對接的是外界溫度，為一個蒸發散熱過程。

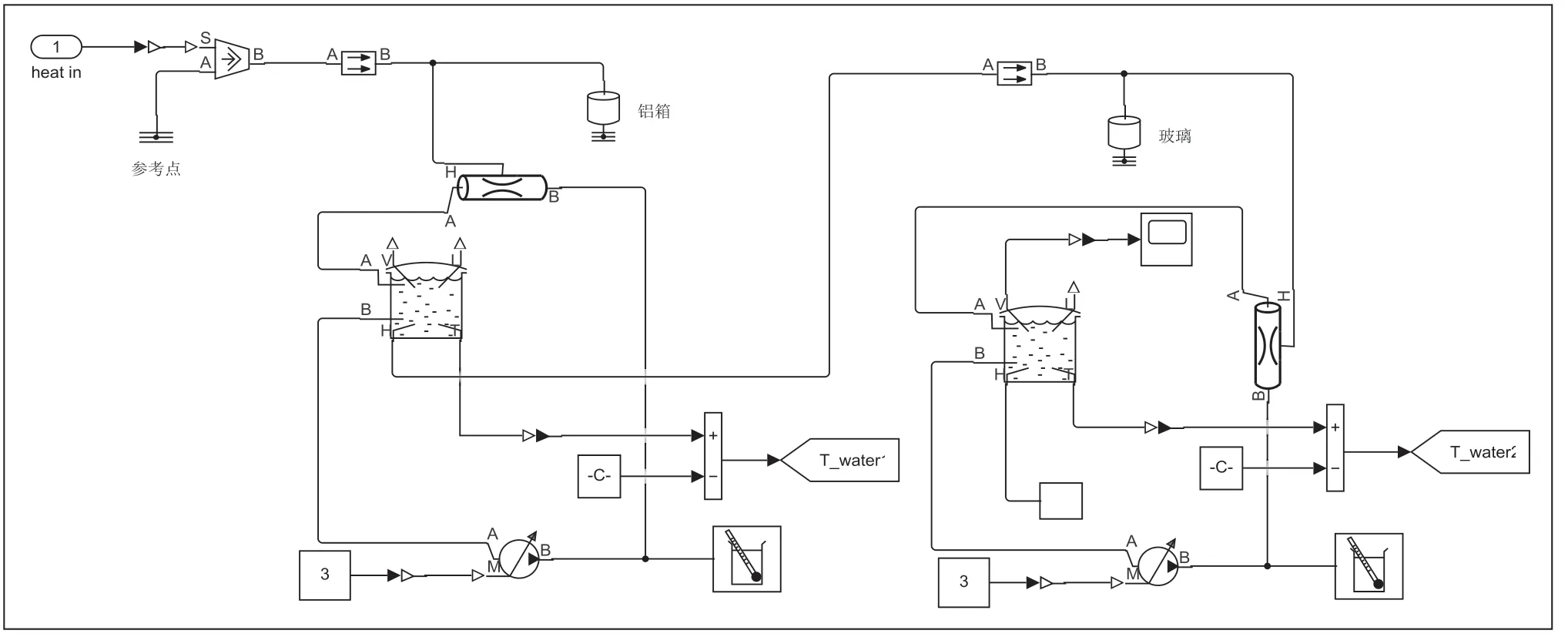
圖1 水浴鍋加熱物理模型

內外鍋傳熱仿真模塊內部見圖2 所示，溫度輸入從TANK(B)端A 端流入，熱源通過TANK(B)的H 口傳遞給TANK(S)的H 端。

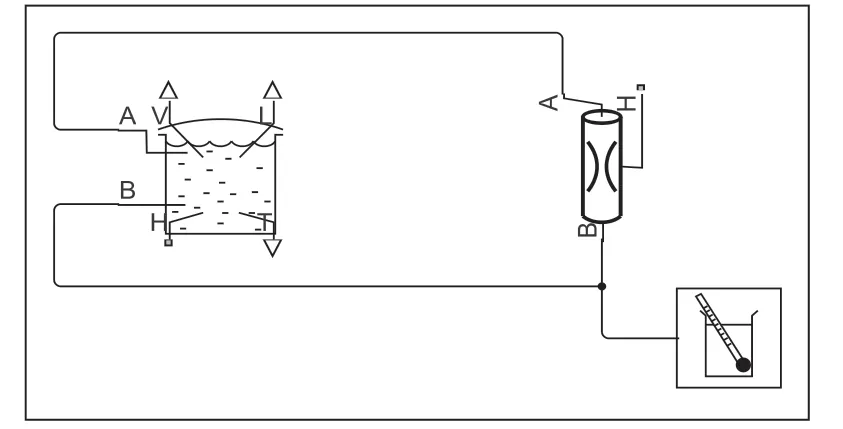
圖2 內外鍋傳熱模型塊

管道能量守恒公式：

熱液與管壁之間的熱流率為：

燒杯內部能量守恒公式：

2 基于Fuzzy-RBF 神經網絡PID 設計

2.1 PID 控制

傳統PID 作為最經典的控制方式，本身有很多優點，結構簡單，調整方便，使用方式是將三個固定的參數比例(kp)、積分(ki)、微分(kd)組合在一起傳遞給被控對象，使系統達到穩定的控制效果。圖3 為傳統PID 控制原理圖。

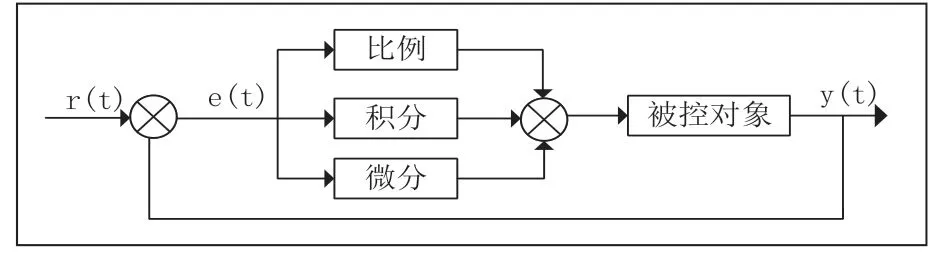
圖3 傳統PID 控制器原理圖

PID 控制器的輸出e(t)與輸出u(t)的關系為[17]：

上式中，Kp是比例系數，Ki是積分系數，Kd是微分系數。

2.2 模糊PID 控制

模糊PID 根據模糊邏輯將輸出值y(t)和給定值r(t)運用模糊規則，經過模糊化、模糊推理、去模糊化三個步驟得到參數通過特定的組合疊加到傳統PID 上，從而達到修正傳統PID 的值，但是模糊PID 對于一些控制系統效果不佳，對于有滯后的、非線性的系統控制起來就顯得吃力，并且模糊PID 中模糊域中參數依賴于工程師的經驗，受人為影響大，這對在以后控制中出現的偏差難以解決，圖4 為模糊PID控制器的結構。

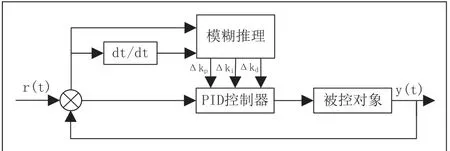
圖4 模糊PID 控制器

2.3 Fuzzy-RBF 神經網絡PID 控制

為了消除模糊 PID 使用時存在人為主觀因素的影響，將模糊控制、RBF 神經網絡和傳統 PID 優點結合到一個控制系統中，使控制系統產生更加穩定的控制效果，見圖5 Fuzzy- RBF 神經網絡 PID 控制器的結構圖，其控制基本原理為：將溫度偏差e(t)與溫度偏差變化率ec(t)輸入到神經網絡中，通過Fuzzy-RBF 神經網絡中模糊控制器的模糊化和模糊推理，對 PID 的三個參數進行在線自我整定，來實現理想的控制效果[12]。

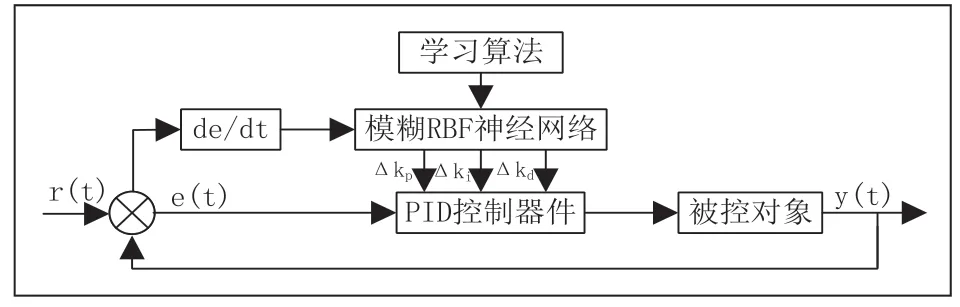
圖5 模糊 RBF 神經網絡 PID 控制器的結構圖

2.4 模糊神經網絡的結構

RBF 神經網絡共有4 個層，分別為輸入層、模糊化層、模糊推理、輸出層，輸入層由兩個節點組成，其作用是接收偏差和偏差變化率，將其傳入下一層模糊化層，主要是根據模糊網絡的規則，將其分為7 個節點，把輸入層的參數生成隸屬度函數，第三層主要是將每個模糊規則的隸屬度函數調節至合適值，然后通過第四層把模糊參數反模糊化，生成輸出層三個參數，分別為kp、ki、kd。圖6 是模糊神經網絡結構圖以及各層的關系式。

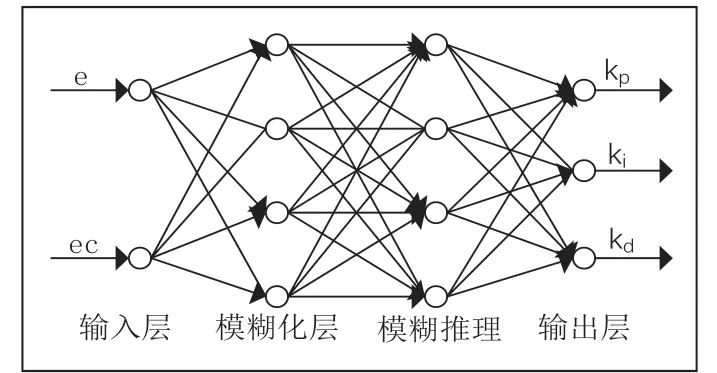
圖6 模糊神經網絡結構圖

第1 層為輸入層。

第2 層為模糊化層。

式中，i= 1,…,N,j= 1,2,3, …,M,cij和bij表示第i 個輸入變量第j個模糊集合隸屬度函數的中心和基寬[12]。

第3 層為模糊推理層。

式中，i1=1,2,…,M,i2=1,2,…,M,n=1,2,…,MN。

第4 層為輸出層。

其中，模糊推理層和輸出層直接用權矩陣w 鏈接，i= 1,2,3。

2.5 模糊神經網絡PID 學習算法

Fuzzy-RBF 神經網絡是利用自身的智能學習能力，重新規劃模糊控制器中的模糊規則，通過線性方式來改變連接權wij、隸屬度函數中心cij和基寬bij，該控制器的輸出為：

PID 算法為：

式中：e(k)為第k次采樣時刻的系統偏差。

自我學習的目標函數：

式中：w分別為該系統在kT時，刻的理想輸出與實際輸出，r(k) -y(k)則表示為迭代步驟k的控制誤差。

本文采用梯度下降法對參數進行計算，通過不斷搜索最小值，使系統中參數達到最優，結束迭代，然后輸出權重wij、隸屬度函數中心cij和基寬bij，具體算法為下式：

式中，α為迭代步驟；α為慣性系數，α∈[0,1]；η為學習效率η∈[0,1]。

2.6 模糊神經網絡PID 學習步驟

（1）初始化系統中c、d、w、η、α。他們分別是隸屬度函數、基寬、權值、學習效率、慣性系數。

（2）根據系統傳遞過程計算，得出溫度差值e(k)以及溫度差變化量ec(k)。

（3）將各個參數傳遞給神經網絡，通過迭代計算出下一次系統輸出的溫度值y(k+)1 。

（4）重新從系統中獲取的參數c、b、w。

（5）令k=k+1 ，繼續采樣，然后返回步驟（1），再進行重新計算。

3 仿真分析

圖7 是Fuzzy-RBF 算法的模型，由于算法結構復雜，神經元數目數目眾多，難以用模塊來搭建其結構，因此采用S 函數來搭建算法，不僅實現了其功能，同時使操作行大大提高，為了檢驗Fuzzy-RBF 算法的性能，分別與普通PID算法、模糊PID 算法對比，通過Simulink 建立的物理模型。

圖7 Fuzzy-RBF 仿真結構圖

首先我們給系統期望值為40 度的初始值，通過三種不同算法檢驗系統到達期望值的時間、超調量、穩定時間，具體參數如圖8 所示。

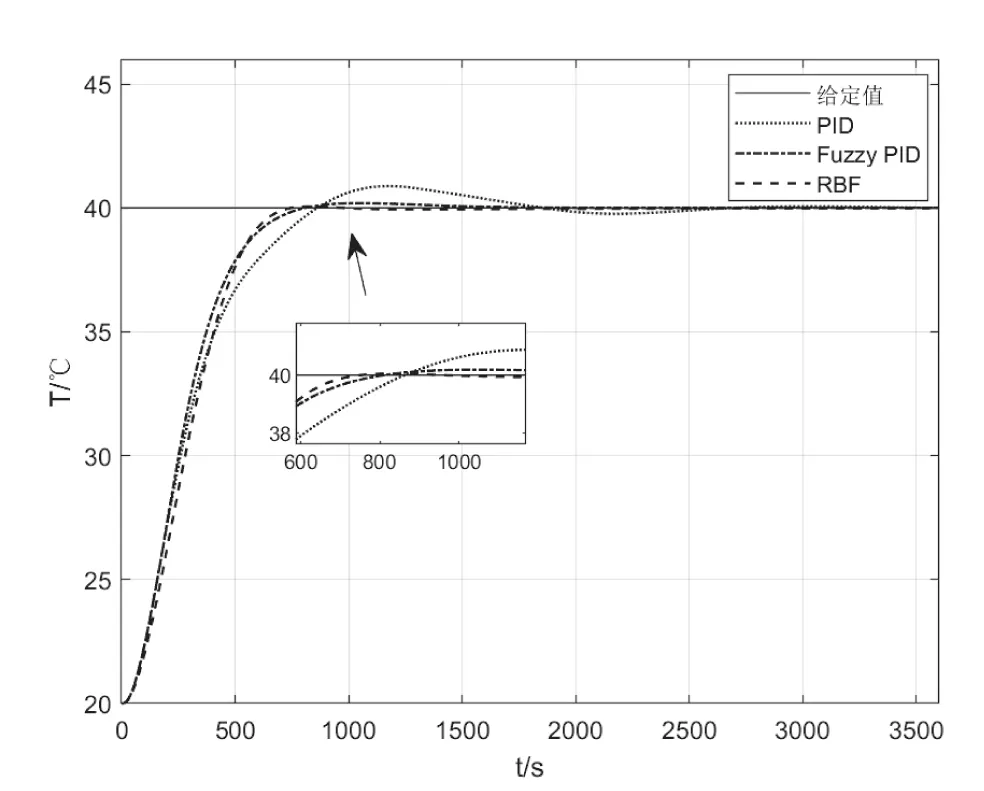
圖8 三種控制方式仿真結果比較圖

通過上面的圖8 和表1 我們可以看到，普通PID 的控制效果最差，達到上升時間為862s，并且該算法在系統中超調量達到了2.199%，最后達到期望穩定的溫度區間需要2335s，模糊PID 的上升時間、超調量、調節時間中的參數雖然優越于普通PID，但對于Fuzzy-RBF 還是有很多不足，Fuzzy-RBF 中的上升時間低于800s，超調量為0.128%，幾乎可以忽略，且調節時間遠遠小于另外兩種算法，通過上述分析，Fuzzy-RBF 神經網絡PID 控制算法在恒溫水浴鍋加熱系統有優越的性能，在控制過程中反應速度快、穩定性好、精度高。

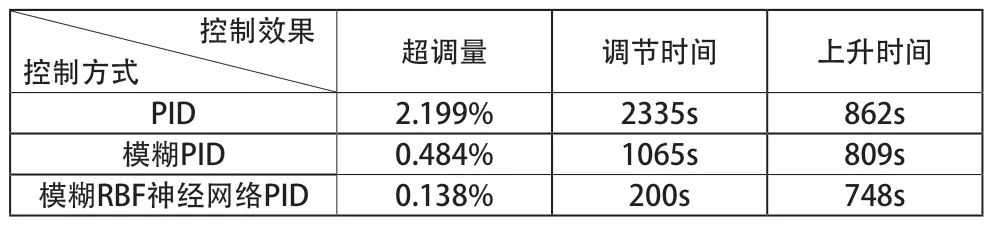
表1 三種控制方法比較數據統計表

圖9 和表2 為檢驗Fuzzy-RBF 神經網絡 PID 控制系統的跟隨效果，首先給水浴鍋物理系統輸入一個40°階躍，使其達到期望的溫度后且穩定后，在 t=2000s 時，再給階躍信號疊加一個溫度為5 的階躍信號，Fuzzy-RBF 神經網絡PID 控制系統是最快達到二次階躍的溫度，從穩態40°到期望的45°僅用了458s，其他兩種控制算法都超過500s，在超調量和調節時間指標下，控制效果都比其他兩種算法好很多，穩定性和波動性效果明顯，Fuzzy-RBF 神經網絡PID控制算法在跟隨階躍上具有良好的跟隨性能和魯棒性。

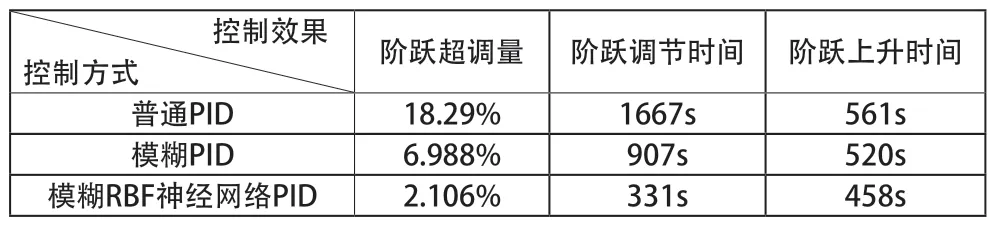
表2 改變輸入信號時三種控制方法比較數據統計表

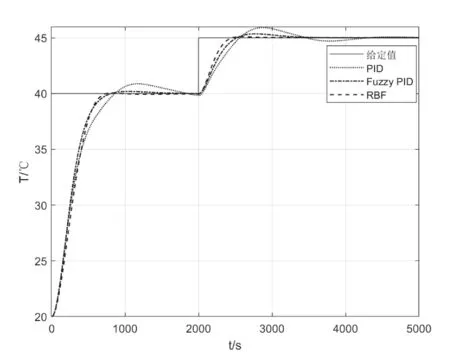
圖9 改變輸入信號時三種控制方式仿真結果比較圖

對于恒溫水浴鍋加熱控制系統，不僅要快速、精準到達期望溫度，還要有一定抗干擾能力，抵抗外界擾動對系統產生影響，本次改變了外界環境的溫度，控制系統溫度穩定后，在3000s 處升高外界的溫度，擾動效果如圖10 和表3 所示，通過比較不難發現，對于同樣的擾動，通過對比，Fuzzy-RBF 神經網絡 PID 控制系統能夠很好抑制外界溫度升高帶來的不穩定現象，同時該算法產生的超調量和調節時間優越于其他兩種。

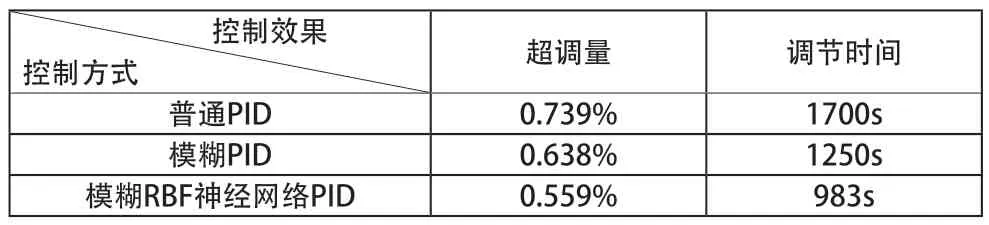
表3 加入擾動時三種控制方式對比圖

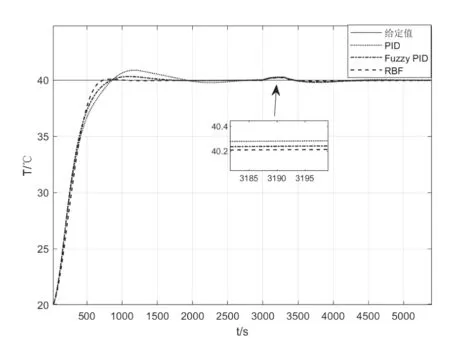
圖10 加入擾動時三種控制方式仿真結果比較圖

4 結論

針對恒溫水浴鍋在搭建數學模型不準確，函數擬合度低的情況，本文建立了基于物理模型的仿真，提出了一種基于Fuzzy-RBF 神經網絡PID 控制系統控制的恒溫水浴鍋加熱，通過Simukink 仿真驗證，在不同期望溫度值，能夠達到期望的效果，實現了對溫度的快速、精確、穩定的控制。