基于Multisim 的分形分抗逼近電路仿真分析

汪志濤，袁曉

（四川大學電子信息學院, 四川成都，610064）

0 引言

近年來，分數(shù)階微積分作為熱門領域受到國內外學者的廣泛研究，并逐步發(fā)展為數(shù)學分析中的一個重要領域[1]。具有分數(shù)階微積分運算功能的電路與系統(tǒng)——分數(shù)階電路與系統(tǒng)[2-3]的研究與應用也越來越廣泛，尤其是具有任意實分數(shù)階微積算子的分抗逼近電路[4]的研究。分抗元件是構建分數(shù)階電路與系統(tǒng)的核心部分，理想μ階分抗元的阻抗函數(shù)為：

式中，s是拉普拉斯變量，也稱為頻率運算變量；μ是分抗元的運算階，取值為分數(shù)時，稱sμ為分數(shù)階算子；F(μ)表示分抗元的集總特征值。

理想的分抗元是不存在的，目前在工程上，往往都是借助整數(shù)階元件(電阻、電容、電感等)構建一個有限的無源二端電路網(wǎng)絡，使得該電路網(wǎng)絡在特定的頻段范圍內具有理想分抗元的運算特性[5～6]，這種電路網(wǎng)絡被稱為分抗逼近電路。經(jīng)典的分形分抗逼近電路, 如負半階Oldham 分形鏈類、任意階Liu-Kaplan 分形鏈、Carlson 分形格分抗逼近電路等。

本文的目的在于借助Multisim 軟件對經(jīng)典的分形分抗逼近電路進行仿真分析，得出分抗逼近電路的幅頻特征和相頻特征曲線，將幅頻特征數(shù)據(jù)通過Matlab 進行差分求導運算得出分抗逼近電路的階頻特征曲線，并運用蒙特卡羅法進行容差分析，得出電路元器件參數(shù)對電路運算性能的影響。從分數(shù)階微積分運算角度——運算階特征和恒相特征兩方面考察分抗電路的運算特性[7～9]。

1 分形分抗逼近電路理論分析

Oldham 等人在20 世紀70 年代初期引進了一類具有負半階運算特征的規(guī)則分形鏈結構——Oldham Ⅰ型分形鏈電路[10～13]，原型電路及其迭代電路如圖1(a)和圖1(b)所示。文獻[4]根據(jù)對偶操作原理構建出同樣具有負半階運算性能的Ⅱ型、Ⅲ型、Ⅳ型分形鏈電路如圖1(c)，圖1(d)，圖1(e)所示。根據(jù)Oldham Ⅰ型分形鏈分抗迭代電路，由迭代算法公式算出它的輸入阻抗序列為：

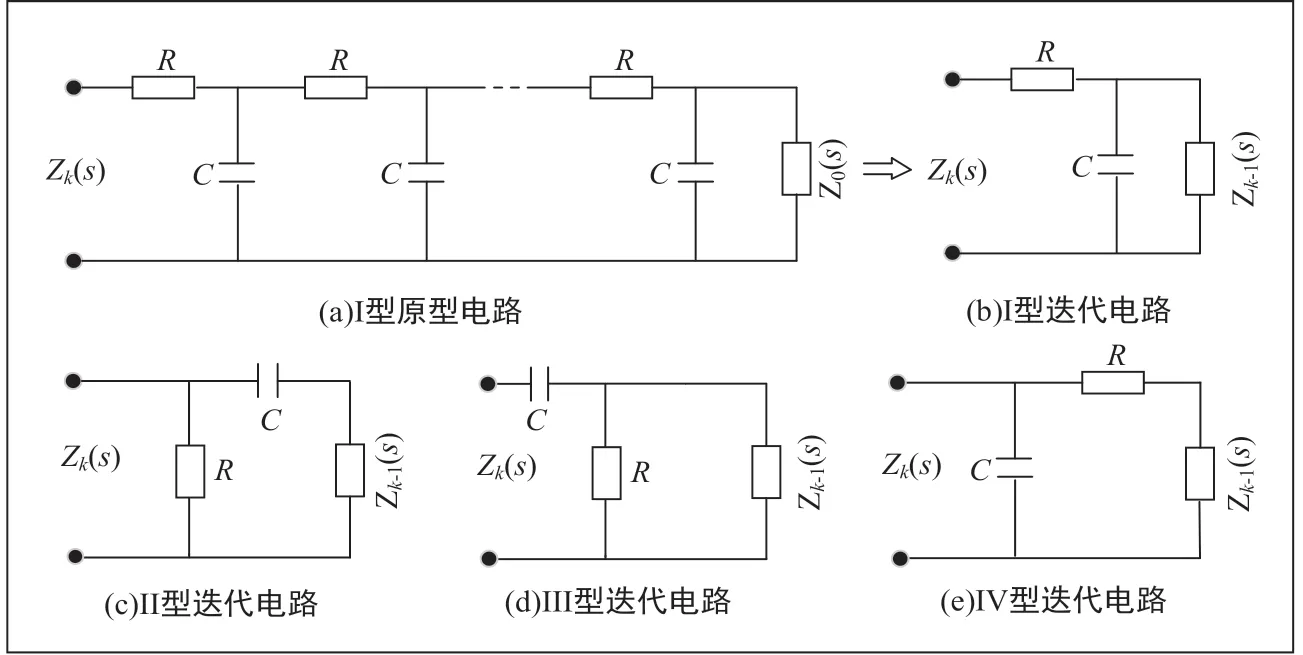
圖1 Oldham 分形鏈類分抗逼近電路

如果令R=a，(Cs)-1=b，Z k(s)=xk，則得到一個代數(shù)迭代運算公式：

式中代數(shù)函數(shù)F(x)(a≠b,x∈?+)稱為Oldham Ⅰ型鏈分抗的迭代函數(shù)，且函數(shù)F(x) 是收斂的，其不動點r即迭代方程式(4)的正實根。

式(2)中當k無窮大時的極限阻抗Z(s) 就是迭代函數(shù)F(x)的不動點r(s)，即有：

式中，Ω0=1RC，是Oldham Ⅰ型鏈分抗的本征頻率。

從式(5)和式(7)可以直接看出，Oldham Ⅰ型鏈分抗逼近理想的負半階分抗不如Oldham Ⅰ型鏈分抗好，并且它們都是在低頻段逼近理想分抗。

式中F(y)稱為Oldham Ⅰ型鏈分抗的歸一化迭代函數(shù)。

表1 Oldham鏈分抗類電路的數(shù)學描述

2 分形分抗逼近電路仿真分析

Multisim14 電路仿真軟件提供了非常齊全的仿真與分析功能[15]，仿真分析方法主要有：交流掃描分析方法 (AC Sweep Analysis) 用于計算電路的頻率響應，輸入信號源都將用設定頻率的正弦信號代替；蒙特卡羅分析 (Monte Carlo Analysis) 采用統(tǒng)計的方法分析元件特性對電路性能的影響；最壞情況分析 (Worst Case Analysis) 也是以統(tǒng)計分析的方式，來研究元件參數(shù)變化時可能對電路性能造成的最壞影響。其中蒙特卡羅分析方法和最壞情況分析方法是電子電路容差分析主要的兩種方法。

借助Multisim 電路仿真軟件，建立起Oldham Ⅰ型鏈分抗仿真電路如圖2 所示，電路中的電阻阻值R=1 k Ω，電容容值C=1μF時，初始迭代值Z0(s) =R= 1 k Ω。

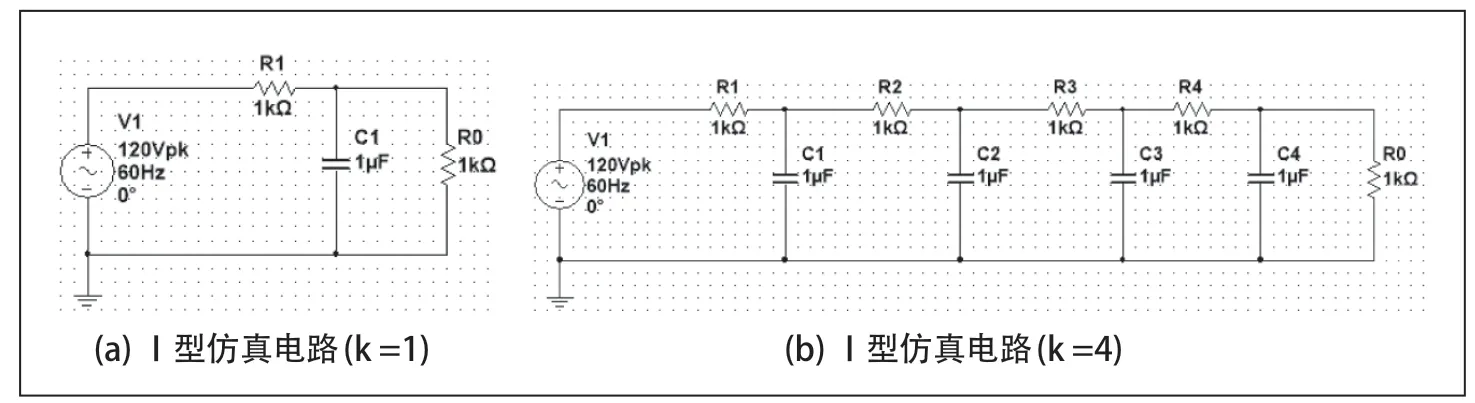
圖2 Oldham Ⅰ型鏈分抗仿真電路

2.1 交流分析

在Multisim 中進行交流掃描分析，設置交流分析的起始頻率為0.0001 Hz，截止頻率為10 kHz，掃描方式為默認的十倍刻度掃描，每十倍頻采樣點數(shù)為100 個，垂直刻度選擇對數(shù)刻度，輸出中選定用于分析的變量為V(1) I(V1) ，既分抗電路的輸入阻抗，當逼近級次數(shù)k分別為1、4、16、64、256 時，運行后得到的幅頻特征曲線和相頻特征曲線數(shù)據(jù)導入到Excel 中，再通過Matlab 進行數(shù)據(jù)處理得出OldhamⅠ型鏈分抗電路輸入阻抗隨迭代次數(shù)（逼近級次數(shù)）k變化的幅頻特征曲線和相頻特征曲線如圖3 (a)和圖3(b)所示，隨著迭代次數(shù)的增大，逼近電路原來越復雜，帶來的逼近帶寬也越來越大。其中虛直線是運算階數(shù)μ=-1 2的理想分抗的頻域特征函數(shù)曲線。圖3 (c)的階頻特征曲線由幅頻特征微分所得，階頻特征和相頻特征可完全表征分抗逼近電路的運算特性。對于一個給定的分抗與分數(shù)階電路系統(tǒng)，考慮其運算階才是首要的。經(jīng)過對比分析，通過Multisim 軟件進行交流仿真分析所得頻域特征曲線與在Matlab 中數(shù)值求解所得的頻域特征曲線幾乎一致，由此可見在Multisim 中進行仿真分析的可行性。

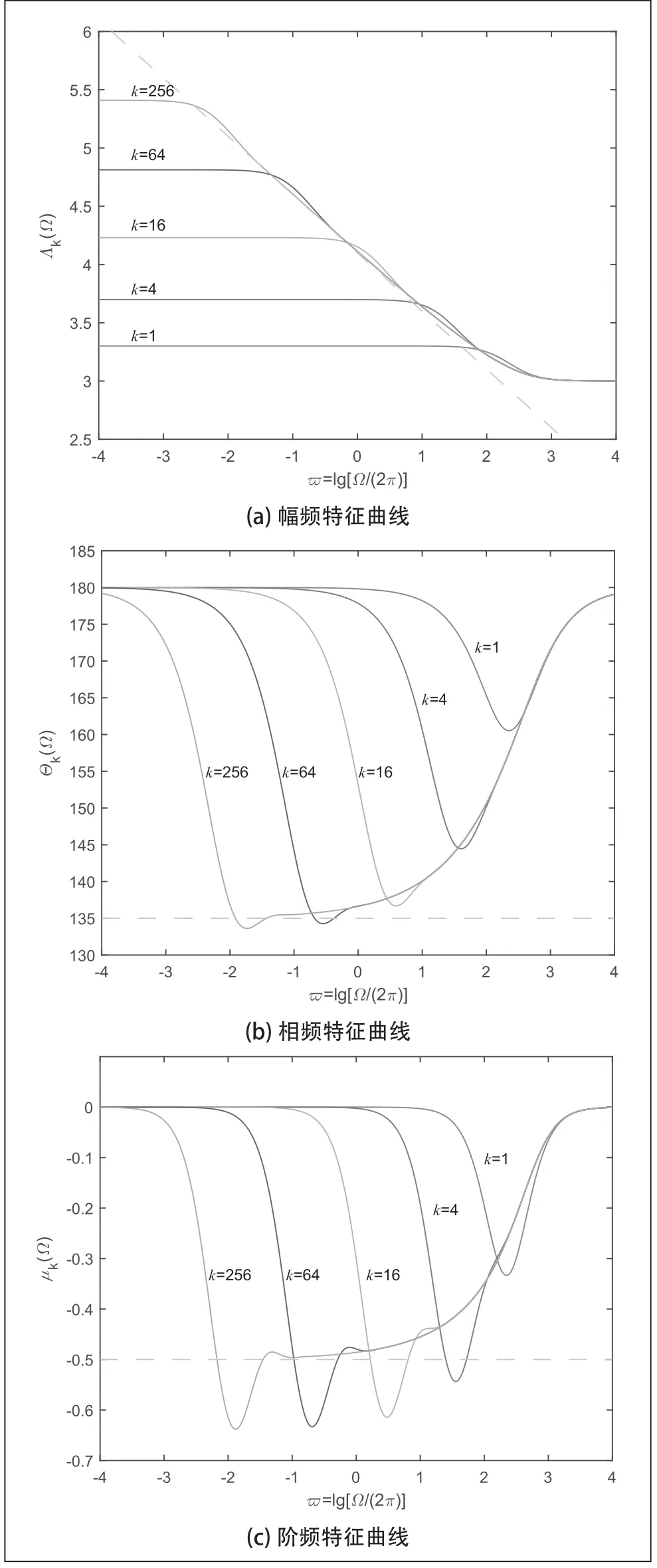
圖3 Oldham Ⅰ型鏈分抗頻域特征曲線

2.2 蒙特卡羅分析

在Multisim 軟件的分析菜單中選擇蒙特卡羅分析，圖2(a)所示的電路分別將電阻 1R阻值、電容 1C容值的容差范圍及其分布規(guī)律選擇正態(tài)高斯分布百分比為50，選擇交流分析類型，蒙特卡羅分析次數(shù)為5，輸出變量為V(1) I(V1) ，既分抗電路的輸入阻抗，啟動并運行后得到圖4 所示的OldhamⅠ型鏈分抗逼近電路 1R、1C標稱值與有50%容差情況下的幅頻響應和相頻響應的曲線簇波形。由蒙特卡羅分析結果，可以看出當元器件參數(shù)值按50%正態(tài)高斯分布規(guī)律隨機變化時，分抗電路的幅頻響應及相頻響應呈現(xiàn)了一定的分散性。

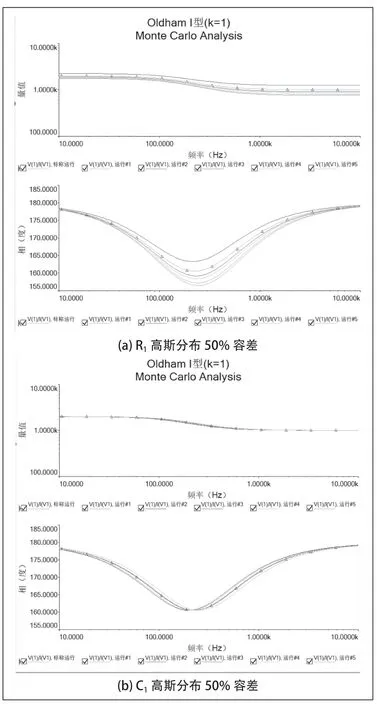
圖4 蒙特卡羅分析結果(k=1)

對應容差分析電路的階頻特征曲線如圖5 所示，根據(jù)分析結果可知k=1 時電阻 1R參數(shù)容差相比于 1C參數(shù)容差對Oldham Ⅰ型鏈分抗逼近電路的運算性能影響更大。對于改進的Oldham型鏈分抗，從式(5) 和式(7)可以直接看出，Ⅰ型改進型鏈分抗逼近理想的負半階分抗效果更好，上述的蒙特卡羅分析結果也是從仿真實驗上證實了這一特性。

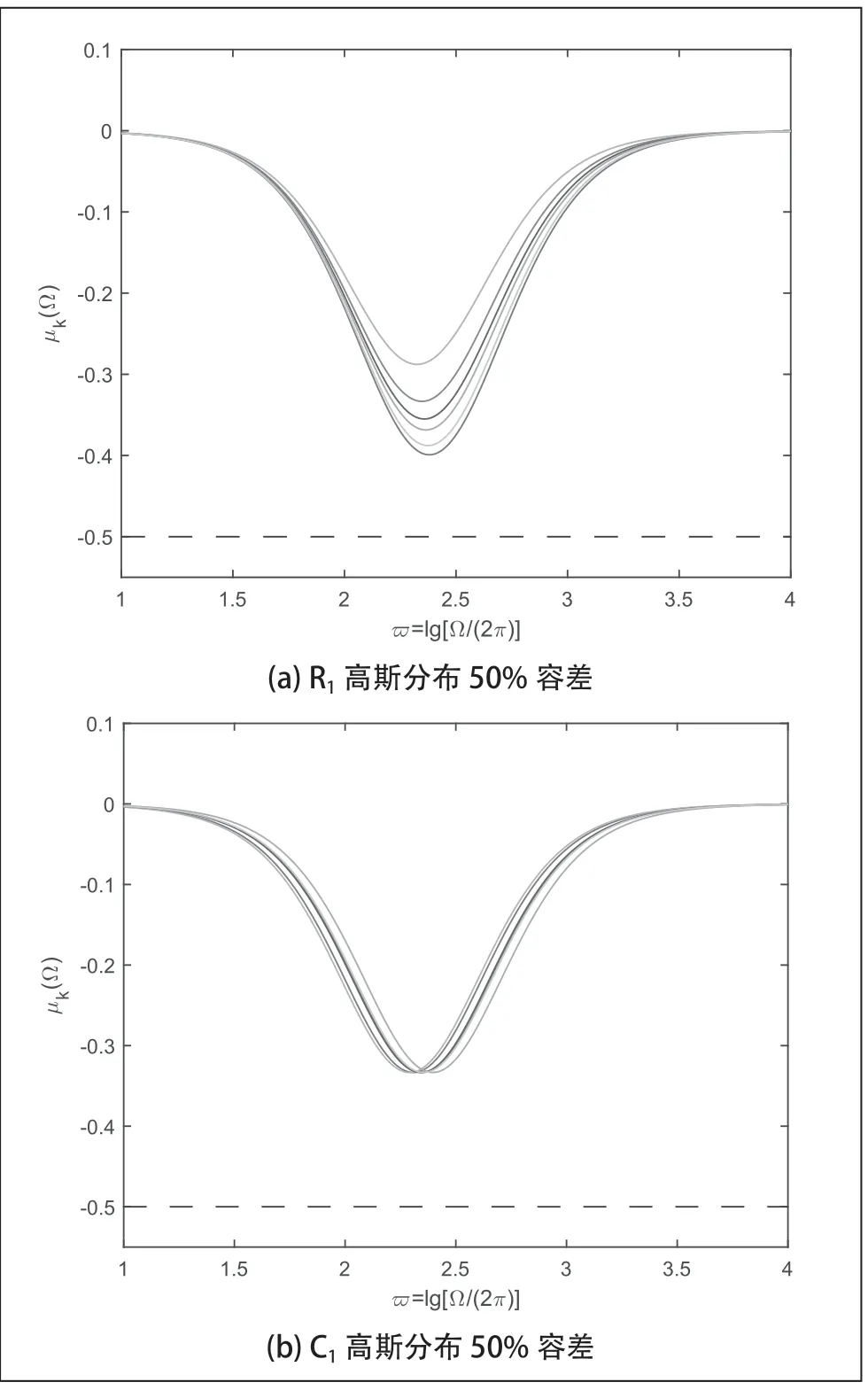
圖5 階頻特征曲線(k=1)

在圖2 (b)所示k=4 時的Oldham Ⅰ型鏈分抗逼近電路中分別將電阻 1R、2R、3R、4R阻值的容差范圍及其分布規(guī)律選擇正態(tài)高斯分布百分比為50，Multisim 軟件中其它仿真設置與k=1 時一致。根據(jù)運行后得到的頻率響應曲線簇波形，通過Matlab 進行數(shù)據(jù)處理得到對應容差分析電路的階頻特征曲線如圖6 (a)所示，可以看出電阻 1R取值分布對分抗電路的運算階影響最大，電阻阻值越接標稱值的一半時，對分抗逼近電路而言所帶來的逼近帶寬越大，并且越靠近初始電阻 0R的電阻參數(shù)容差對電路運算階的影響越小，所以在工程中進行電路設計時，對電阻 1R阻值的精度要求更嚴格，電阻 1R的容差越小越好。

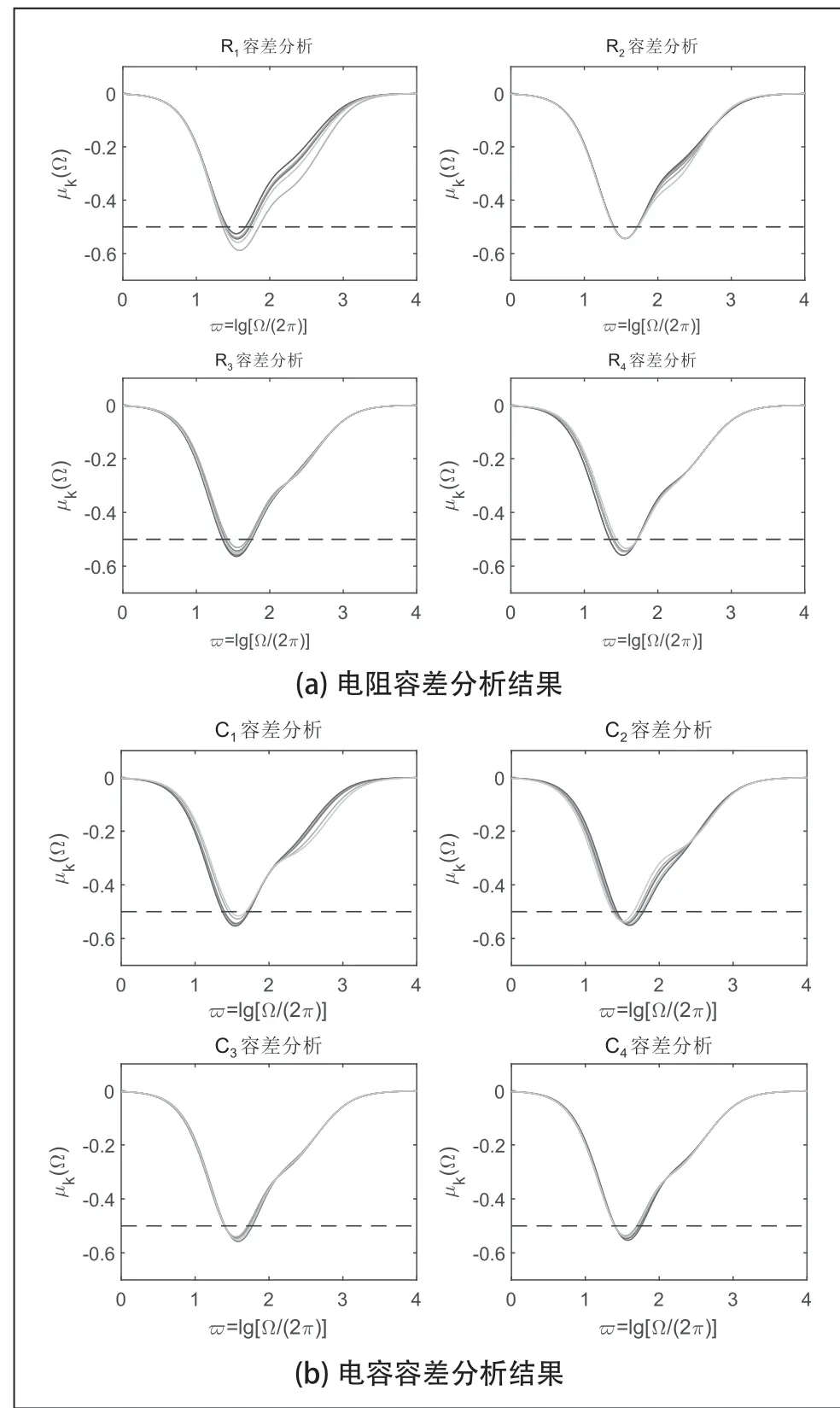
圖6 容差分析階頻特征曲線(k=4)

再將k=4 時的Oldham Ⅰ型鏈分抗逼近電路中分別電容 1C、C2、3C、C4的參數(shù)容差范圍及其分布規(guī)律選擇正態(tài)高斯分布百分比為50，其它設置與對電阻進行容差分析時一致。進行蒙特卡羅分析后得到頻率響應曲線簇波形，圖6 (b)為將數(shù)據(jù)導入Matlab 進行處理后得到各個電容對應容差分析的分抗電路的階頻特征曲線。經(jīng)過分析得出越靠近初始電阻 0R的電容參數(shù)容差對電路運算階的影響越小，相反，1C的容差對電路運算性能的影響最大，意味著在工程上設計分抗電路時，電容 1C的容差也是越小越好。

3 結論

由以上分析結果可以看出，利用Multisim 軟件可以方便快速地對分抗逼近電路進行仿真，通過交流分析可以得出電路的幅頻特征和相頻特征，蒙特卡羅分析方法通過改變電路元件的參數(shù)，可以得到不同電路元件參數(shù)容差對電路運算性能的影響，十分便于我們從分數(shù)階微積分運算的角度考察分抗電路的運算特性，為分抗電路可靠性設計提供有意義的依據(jù)，從而節(jié)省設計時間與設計費用，提高電子產(chǎn)品的設計效率。