學(xué)情前測：精準(zhǔn)把握單元整合的有效手段

于飛

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》（以下簡稱“新課標(biāo)”）中提出要重視單元整體教學(xué)設(shè)計，并指出：“單元整體教學(xué)設(shè)計要整體分析數(shù)學(xué)內(nèi)容本質(zhì)和學(xué)生認(rèn)知規(guī)律，合理整合教學(xué)內(nèi)容，分析主題—單元—課時的數(shù)學(xué)知識和核心素養(yǎng)主要表現(xiàn)，確定單元教學(xué)目標(biāo)，并落實到教學(xué)活動各個環(huán)節(jié)，整體設(shè)計， 分步實施，促進(jìn)學(xué)生對數(shù)學(xué)教學(xué)內(nèi)容的整體理解與把握，逐步培養(yǎng)學(xué)生的核心素養(yǎng)。”“前測”是教學(xué)前為了準(zhǔn)確把握學(xué)情，教師設(shè)計有針對性的評測題，對學(xué)生進(jìn)行測試，然后根據(jù)測試數(shù)據(jù)，提出相應(yīng)的教學(xué)改進(jìn)策略，做到以學(xué)定教。那么，前測“前”，教師應(yīng)該思考什么？前測“題”，應(yīng)該如何定位目標(biāo)？前測“數(shù)據(jù)”，應(yīng)該反映什么問題？前測“后”，應(yīng)該如何進(jìn)行教學(xué)改進(jìn)？筆者以人教版數(shù)學(xué)教材三年級下冊第四單元“兩位數(shù)乘兩位數(shù)”單元教學(xué)為例做一些探討。

一、思單元整體

（一）整體分析——關(guān)鍵期與轉(zhuǎn)折點

“兩位數(shù)乘兩位數(shù)”是整數(shù)乘法學(xué)習(xí)的關(guān)鍵期和轉(zhuǎn)折點，它是學(xué)生在二年級上冊學(xué)習(xí)了表內(nèi)乘法，三年級下冊學(xué)習(xí)了多位數(shù)乘一位數(shù)的基礎(chǔ)上教學(xué)的，也是為四年級上冊學(xué)習(xí)三位數(shù)乘兩位數(shù)做筆算表征知識的準(zhǔn)備。筆算豎式表征從多位數(shù)乘一位數(shù)“一層”跨越到兩位數(shù)乘兩位數(shù)“兩層”，是豎式表征形式上的一次飛躍，但運(yùn)算的算理和算法又是相通的，原理都是“拆分”。“兩層”豎式掌握了，四年級上冊的三位數(shù)乘兩位數(shù)，以及更多層數(shù)的筆算，學(xué)生就能自主遷移了。

（二）單元分析——小步走與析學(xué)情

筆者發(fā)現(xiàn)，人教版教材的編排步子較小，本單元的學(xué)習(xí)重點是理解和掌握兩位數(shù)乘兩位數(shù)的筆算乘法算理和算法。而“口算乘法”安排3課時，為筆算乘法所做的鋪墊為：兩位數(shù)乘一位數(shù)關(guān)聯(lián)乘法豎式第一層，兩位數(shù)乘整十?dāng)?shù)關(guān)聯(lián)第二層，內(nèi)容劃分過細(xì)，忽略了真實學(xué)情（如表1）。

基于以上單元整體分析，筆者設(shè)想整合這一單元口算乘法“兩位數(shù)乘一位數(shù)”“兩位數(shù)乘整十?dāng)?shù)”和筆算乘法“兩位數(shù)乘兩位數(shù)”（不進(jìn)位）”為1課時，將口算乘法中的“拆分”融于豎式計算中，充分展開“拆分”的教學(xué)，溝通聯(lián)系豎式，理解每一步的含義，最后拓展到四年級上冊“三位數(shù)乘兩位數(shù)”，以提高學(xué)生的遷移能力。

二、定前測目標(biāo)

為了準(zhǔn)確把握學(xué)情，通過思考第1課時能否基于單元整體分析進(jìn)行有效的內(nèi)容整合，筆者擬定了如下前測題（“兩位數(shù)乘兩位數(shù)”前測單）。

1.直接寫得數(shù)：

15×3= 150×3= 15×6= 150×6= 6×10= 18×10= 12×20= 120×20=

2.用你想到的或者喜歡的方法，計算出14×12的得數(shù)，寫出必要過程。

3.列豎式計算（學(xué)生沒學(xué)過，有挑戰(zhàn)）：12×44= 48×37=

前測目標(biāo)為：

第1題，題目選自教材第41～42頁例題及“做一做”，意在檢測學(xué)生對兩位數(shù)乘一位數(shù)和兩位數(shù)乘整十、整百數(shù)的掌握情況，即口算乘法，少教，甚至不教，是否可行？

第2題，題目選自教材第46頁例題，但不限定方法，用自己喜歡或者想到的方法，算出得數(shù)。檢測學(xué)生是否能用“拆分”的方法，將新知轉(zhuǎn)化為舊知，即拆分，學(xué)生會嗎？

第3題，題目選自教材第47頁練習(xí)題及第49頁例題，限定方法，只能用豎式計算。檢測第2題學(xué)生采用“拆分”的方法，第3題能否成功列出“兩層”豎式以及進(jìn)位乘法對學(xué)生影響有多大，即會拆分與會豎式之間有多大距離？

以上3題的前測目標(biāo)，均圍繞預(yù)設(shè)的單元整體設(shè)想，采集有針對性的數(shù)據(jù)和典型案例。

三、析數(shù)據(jù)價值

為保證樣本數(shù)據(jù)的真實性和代表性，筆者選取了本校4位教師任教的4個不同班級共178名學(xué)生進(jìn)行了前測，數(shù)據(jù)如表2、表3和表4。

（一）口算乘法要少教

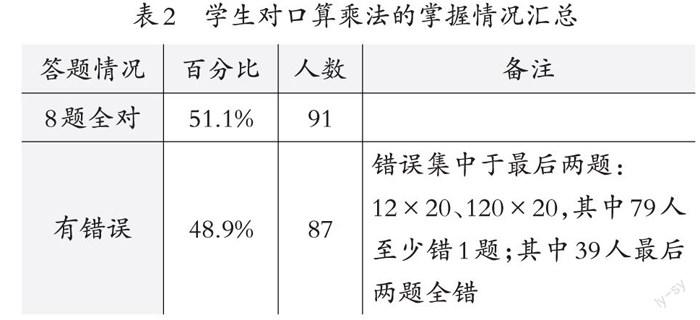
表2數(shù)據(jù)反映：

1.超過一半的學(xué)生對兩位數(shù)乘一位數(shù)的口算掌握得很好，該知識點因此可以不作為完整一課時單獨教學(xué)。

2.學(xué)生對兩位數(shù)乘整十?dāng)?shù)、整百數(shù)的口算，還存在一定問題，需要關(guān)注學(xué)生在口算時對“拆分”和末尾添0的理解和熟練運(yùn)用。

表3數(shù)據(jù)反映：超過60%的學(xué)生在不限定方法時，能通過自主嘗試求出14×12的積，并且有合理的過程。這其中采用“拆分”且計算正確的人數(shù)占到正確總?cè)藬?shù)的68.5%，說明學(xué)生對于“拆分”的原理已經(jīng)有了較強(qiáng)的理解，能夠運(yùn)用此方法將新知轉(zhuǎn)化成舊知。不管是正確的還是錯誤的，采用“豎式”計算的學(xué)生人數(shù)都比采用“拆分”的人數(shù)少很多。

表4數(shù)據(jù)反映：限定豎式計算，正確率比不限定下降明顯，僅有26.4%的學(xué)生兩題豎式計算正確，而做對的47人中的38人，還是前測第2大題也采用“兩層”豎式計算的學(xué)生，正確轉(zhuǎn)化率高達(dá)95%。但是，僅有9位學(xué)生能從第2大題時的拆分轉(zhuǎn)化到豎式計算，并正確，正確轉(zhuǎn)化率僅有13%。這表明“會拆分”與“會豎式”之間看似是一層窗戶紙，實則猶如一條鴻溝難以跨越。兩題全對47人，做對1題9人，這表明“進(jìn)位乘法”對于已經(jīng)掌握兩層豎式的學(xué)生而言，并沒有太大挑戰(zhàn)。表內(nèi)乘法的難點不在于進(jìn)位，而是從“一層”到“兩層”這中間的飛躍。

基于以上3道前測題的目標(biāo)設(shè)定，以及相關(guān)數(shù)據(jù)分析，筆者得到了如下4條教學(xué)啟示：一是減少甚至取消口算作為完整一課時的節(jié)數(shù)，但要關(guān)注兩位數(shù)乘整十?dāng)?shù)的口算，可以通過拆分和末尾添0熟練計算；二是增加拆分方法與直觀圖形“形、式”的溝通，充分理解算理算法，在會拆分與會豎式的鴻溝之間，架起溝通的橋梁；三是整合兩位數(shù)乘兩位數(shù)與三位數(shù)乘兩位數(shù)筆算，溝通聯(lián)系；四是弱化進(jìn)位筆算，不作為完整一課時教學(xué)，引入拓展課。

因此，本單元兩位數(shù)乘兩位數(shù)計算部分，筆者對課時內(nèi)容劃分作如表5調(diào)整。

四、促理法遷移

筆者將本課整合為一節(jié)新課：兩位數(shù)乘兩位數(shù)（不進(jìn)位），進(jìn)行了如下教學(xué)設(shè)計。

（一）口算引入，強(qiáng)化口算過程，為筆算乘法做鋪墊

根據(jù)前測第1題的數(shù)據(jù)反映，學(xué)生對于口算乘法總體已經(jīng)有較強(qiáng)的基礎(chǔ)，特別是兩位數(shù)乘一位數(shù)。雖然兩位數(shù)乘整十、整百數(shù)有一定錯誤率，但仔細(xì)分析，其實質(zhì)主要還是在于如何“拆分”以及末尾添0。因此，在口算引入環(huán)節(jié)，主要是讓學(xué)生表達(dá)清楚是怎么口算的，無論是拆分的方法，還是末尾添0，要讓學(xué)生充分表達(dá)，為筆算乘法做知識上的鋪墊。

【課件出示】 15×3= 23×4= 12×20= 31×30=

150×3= 230×4= 12×200= 310×30=

【要求】課件逐一閃現(xiàn)每題，讓學(xué)生說一說是怎么口算的。主要關(guān)注最后兩組題目學(xué)生的說理過程。

（二）自主嘗試，溝通“拆分”與“豎式”間的聯(lián)系

筆算兩位數(shù)乘兩位數(shù)的原理是“拆分”，兩層豎式只是一種比較合理、簡潔的表征方式。因此，教學(xué)重點不是用怎樣的豎式計算，因為對于從來沒有見過兩層豎式的學(xué)生而言，要其自主“創(chuàng)造”出兩層，這是極其有挑戰(zhàn)的，而那些已經(jīng)會用兩層豎式計算的學(xué)生，也都是課外提前知道了有兩層豎式。所以，溝通“拆分”與“豎式”之間的聯(lián)系，使學(xué)生理解每一步的含義，才是教學(xué)的真正重點。

【課件出示】每套書有14本，王老師買了12套。一共買了多少本？

【要求】（1）自主嘗試，用自己喜歡或者想到的方法，寫出完整過程，算一算；（2）小組交流，結(jié)合點子圖，圈一圈，畫一畫，說說你是怎么算的？（3）投影典型計算方法（如圖1），問學(xué)生看懂了哪種方法，分享交流。

1.理解拆分

生：第一幅圖是把12拆成10+2，10個14+2個14，140+28=168。

生：第二幅圖是把14進(jìn)行了拆分，分成了10和4，10個12+4個12，等于120+48=168。

生：第三幅圖是把12拆成了9和3，因為14×9，14×3，兩位數(shù)乘一位數(shù)是可以口算的，126+42=168。

師：雖然它們看上去都有點不一樣，但本質(zhì)都是相同的，你知道是什么？

生：都用到了拆分的方法，把其中一個兩位數(shù)拆分成兩個一位數(shù)，或者是一個10，一個一位數(shù)。都可以進(jìn)行口算。

2.溝通豎式

師：有一位同學(xué)是這樣做的（如圖2），你能看懂嗎？

用喜歡的方法，算出14×12

生：它用的是豎式計算。

師：這個豎式和我們以前學(xué)的有什么不一樣？又和剛才的拆分方法有什么聯(lián)系？

生：它是兩層的豎式，我們以前學(xué)的是一層的豎式。12的2先和14相乘得到28，然后12的10和14相乘得到140，最后相加得168。

師：這位同學(xué)的豎式，其實和哪位同學(xué)的拆分是一樣的？

生：和圖1中的第二幅圖是一樣的，都是把12拆成10和2，分別和14相乘，最后相加。

師：是的，用第二個因數(shù)12中的每個數(shù)分別與第一個因數(shù)14相乘，最后把兩個積28和140相加，得到最后的結(jié)果168。那為什么兩位數(shù)乘兩位數(shù)的豎式要兩層呢？而以前的豎式只有一層。

生：因為以前多位數(shù)乘一位數(shù)，第二個因數(shù)只有一個數(shù)字，只需要計算1次，而現(xiàn)在第二個因數(shù)是兩位數(shù)，拆分后要計算兩次，所以是兩層。

生：如果14×12也用一層豎式的話，和拆分的方法就對應(yīng)不起來了，一層要計算兩個不同的算式，容易出錯。

（三）學(xué)會遷移，類推三位數(shù)乘兩位數(shù)，探理法相通

兩位數(shù)乘兩位數(shù)是整數(shù)乘法的關(guān)鍵期和轉(zhuǎn)折點，學(xué)生理解和掌握了，有助于遷移類推到三位數(shù)乘兩位數(shù)，因為二者在算法和算理上是相通的，豎式的表征形式也都是兩層。因此，在本課時教學(xué)中，可以作為拓展部分，讓學(xué)生根據(jù)今天所學(xué)知識延伸拓展探究三位數(shù)乘兩位數(shù)的筆算。通過4個大問題，檢測學(xué)生遷移能力。

【問題1】兩位數(shù)乘兩位數(shù)的筆算是兩層的豎式，那三位數(shù)乘兩位數(shù)，你知道豎式會是幾層嗎？先想一想。

生：3層。

生：還是2層。

【問題2】到底三位數(shù)乘兩位數(shù)豎式是幾層？算一算123×21，驗證你的猜想。

（學(xué)生獨立嘗試豎式計算123×21，一位學(xué)生在黑板上板書：兩層）

【問題3】豎式計算時跟這位同學(xué)一樣，也是兩層的請舉手，為什么還是兩層？

生：因為都是用下面的因數(shù)去乘上面的因數(shù)，21的1去乘123得到第一層123，21的20去乘123得到第二層2460。方法和14×12是一樣的。

【問題4】三位數(shù)乘兩位數(shù)要到四年級上冊才學(xué)習(xí)，為什么你們現(xiàn)在就會了？

生：因為三位數(shù)乘兩位數(shù)的計算方法和今天學(xué)習(xí)的兩位數(shù)乘兩位數(shù)方法是一樣的，都是拆分第二個因數(shù)，然后分別和第一個因數(shù)相乘，最后加起來。

以上是我們基于前測實證研究“兩位數(shù)乘兩位數(shù)”單元整合思路與第1課時實踐，闡述了如何基于單元整體分析，研制有針對性的前測題，再結(jié)合數(shù)據(jù)分析，進(jìn)行單元整合教學(xué)。在本課中展現(xiàn)的數(shù)據(jù)實證研究為優(yōu)化單元整體結(jié)構(gòu)、促進(jìn)理法的深度遷移提供了重要的方向支撐。

（責(zé)任編輯：楊強(qiáng)）