是巧合還是必然

程峰 鮑光發(fā)

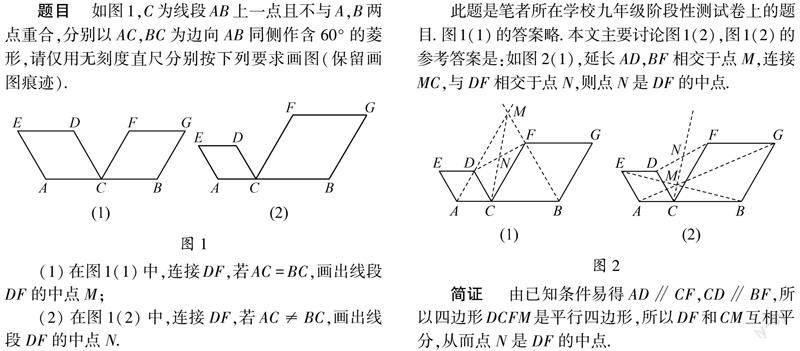
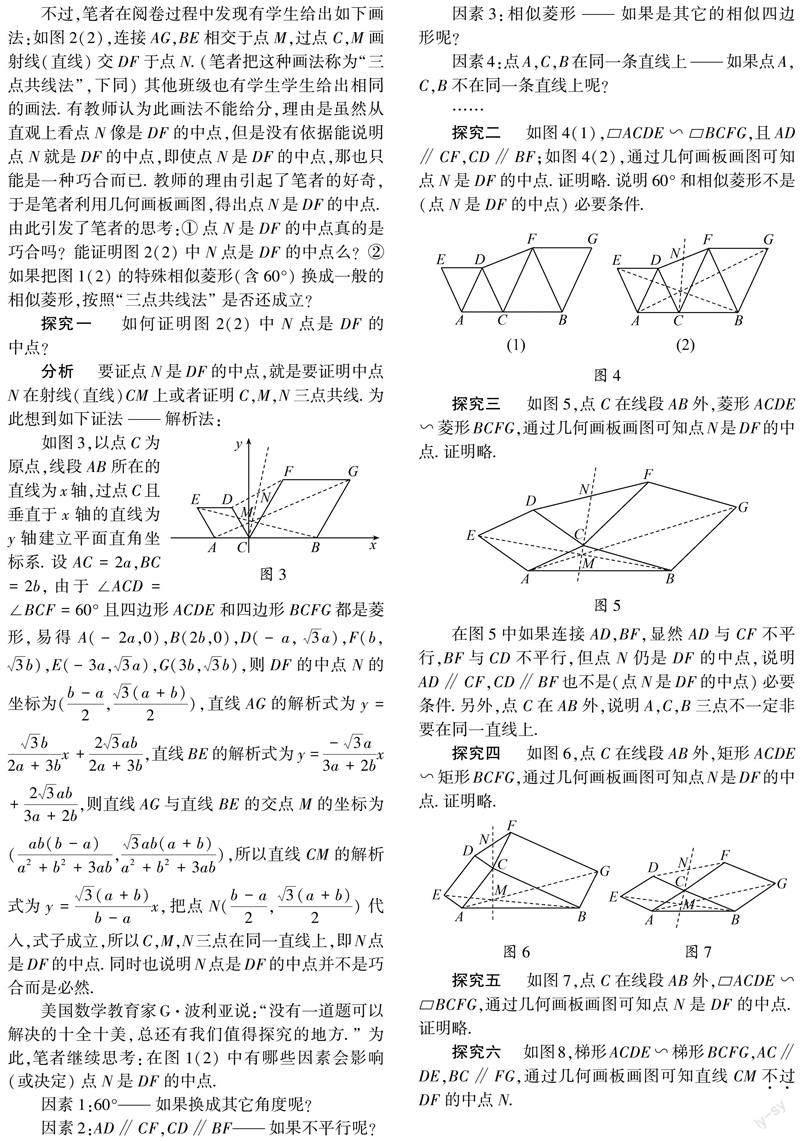
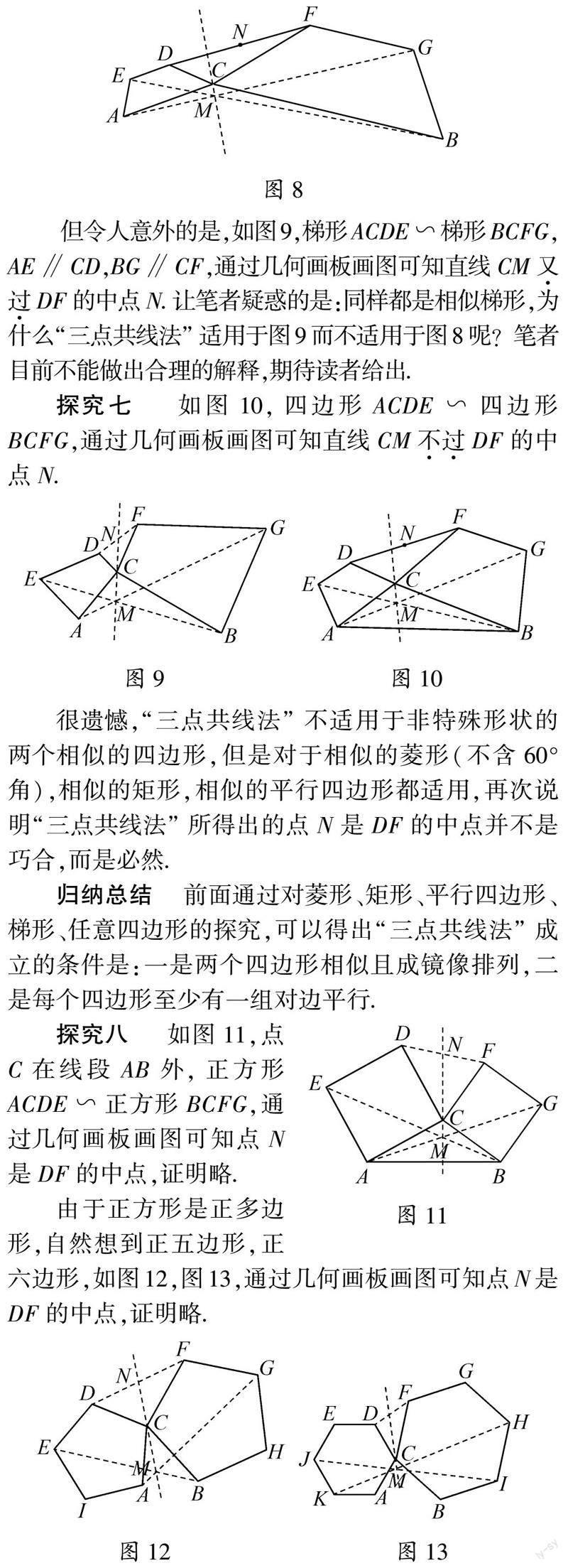
【摘?要】?一道用無刻度直尺的畫圖題，由于學生的畫法不同于參考答案且難以確定畫法是否正確，因此被老師認為是巧合，缺乏依據(jù)，從而引發(fā)了筆者的思考和探究.

【關鍵詞】?巧合；必然；相似菱形；探究；三點共線法

顯然“三點共線法”還適用于正多邊形（正四邊形，正五邊形，正六邊形），由此猜想“三點共線法”適用于正n邊形（n≥4）.

筆者在講評試卷時花了大半節(jié)課專門講解此題，學生既興奮又驚訝，紛紛發(fā)出感嘆，一道小小的畫圖題竟然可以挖掘出這么多相關的問題.

教學啟示

1.思畫法之理，提升思維的嚴密性

有許多學生在解決僅用無刻度直尺的畫圖題時，毫無目的地用刻度尺把所有能連的兩個點連起來，線是畫了不少，但是沒能找出真正有用的點或線，導致問題還是沒有解決.即使碰巧畫對了，思維也沒得到任何提升.筆者在教學時要求學生在連線的過程中就要邊思考，為什么要連這條線，有什么用途，依據(jù)何在，也就是明確畫法后面隱藏的道理，經常這樣思考，就能形成良好的合乎邏輯的思維品質，從而提升思維的嚴密性.本題運用解析法證明了點N是DF的中點，讓學生理解“三點法”的依據(jù)，打消了學生的疑惑，讓學生知其然也知其所以然.

2.悟一法多用，培養(yǎng)思維的發(fā)散性

在教學過程中，要從不同的認識層次，觀察角度，知識背景和問題特點進行一題多變，一法多用，這樣不僅能調動學生學習數(shù)學的興趣，養(yǎng)成積極思考的習慣，而且能培養(yǎng)學生深度思考和分析問題、解決問題的能力，從而在潛移默化中提升發(fā)散性思維.本題從特殊的菱形到一般菱形到矩形到平行四邊形再到正多邊形，發(fā)現(xiàn)用“三點法”都可以找到DF的中點，這樣學生對“三點法”有了更深層次的理解，同時也培養(yǎng)了學生思維的發(fā)散性.

3.明探究過程，培養(yǎng)探究能力

數(shù)學新課標的理念之一是“自主探究，合作交流”.如何讓學生有自主探究的意識，知道怎樣去探究，筆者認為教師自己首先要有自主探究的意識和習慣，才能更好地引領學生探究.教師要善于發(fā)現(xiàn)值得去探究的資源.本題筆者用幾何畫板驗證了點N是DF的中點，并給出了證明，但并沒有就此停下，而是進行更深層次的思考和探究.在講解此題時，筆者把對此題的探究歷程展示給學生，讓學生對“探究”一詞有更深層次的認識和理解，當然對此題也有了新的認識和理解.

參考文獻

[1]周煉.談“作圖題”教學[J].中小學數(shù)學（初中版），2020（9）：39-42.

[2]易良斌.注重幾何直觀強化邏輯推理豐富數(shù)學模型——2018年杭州市中考數(shù)學第23題賞析及教學啟示[J].教學月刊·中學版（教學參考），2018（10）：58-62.

作者簡介

程峰（1975—），男，中小學高級教師;主要研究課堂教學、解題（變式）教學等;發(fā)表文章20余篇.

鮑光發(fā)（1971—），男，中小學高級教師;主要研究初中數(shù)學課堂教學;曾獲市級比賽課一等獎.