國外中小學代數(shù)推理研究的主要成果及其啟示

謝春艷 黃娜娜 潘禹辰 徐文彬

【摘?要】?支持代數(shù)推理能力發(fā)展的基礎性與連貫性，是國外中小學代數(shù)推理研究的基本特征.具體而言，其代數(shù)推理研究從算術與代數(shù)、算術思維與代數(shù)思維的區(qū)別與聯(lián)系出發(fā)，提出“早期代數(shù)”的可行性，繼而從代數(shù)推理的認知分析與發(fā)展策略兩個方面展開深入研究，呈現(xiàn)出理論與實踐互相補充的大致發(fā)展趨勢.由此，我國中小學代數(shù)推理研究應該提高對概念理解的重視程度，考慮代數(shù)推理任務的連貫性，促進教師專業(yè)發(fā)展，以改善算術與代數(shù)教學割裂的現(xiàn)實狀況.

【關鍵詞】?代數(shù)推理；代數(shù)思維；認知分析；發(fā)展策略

代數(shù)在不同國家的現(xiàn)行中小學數(shù)學課程中基本都處于核心地位，而真正關注到（低年級）代數(shù)教學的重要性是在2000年之后.代數(shù)作為一種解決問題的工具，為分析數(shù)量之間的關系、建立模型以及說明和證明提供了一般化的語言和結構，而代數(shù)思維中代數(shù)推理能力的培養(yǎng)是代數(shù)教學的核心問題.國外代數(shù)推理研究要早于國內(nèi)，研究成果也較為成熟.本研究試總結國外代數(shù)推理研究的主要成果，并為國內(nèi)相關研究的開展提出若干啟示.

1?研究概貌

在“Web of Science”中以“Algebraic Reasoning”為標題進行檢索，數(shù)據(jù)庫選擇SCI-Expanded、SSCI、CPCI-S和CPCI-SSH，截至2022年8月，共檢索到77篇文獻，經(jīng)篩選得到相關性較高的文獻16篇.同時在“ERIC”中以“Algebraic Reasoning”為主題詞進行檢索，共檢索到419篇文獻，經(jīng)閱讀排除無關或低相關文獻，得到文獻74篇.在相關中文文獻閱讀過程中補充了12篇外文文獻，最終以102篇代數(shù)推理研究文獻作為分析對象，其中，期刊論文64篇，會議論文30篇，研究報告8篇.

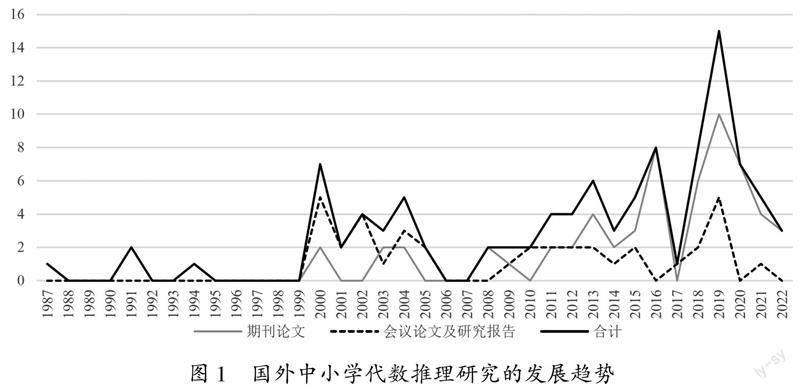
1.1?年度分布

如圖1所示，國外的中小學代數(shù)推理研究自2000年后表現(xiàn)出小幅波動的發(fā)展態(tài)勢.期刊論文與會議論文數(shù)量相差不大，2010年之前以會議論文及研究報告居多，這類研究常出現(xiàn)在數(shù)學教育研究、數(shù)學教育心理學研究等國際會議上；2010年之后期刊論文數(shù)量逐步增加，會議論文數(shù)量基本持平，“代數(shù)推理”仍然是國際會議中關心的問題.與此同時，更多數(shù)學教育者對“代數(shù)推理”的數(shù)學教育實踐展開行動干預，給出調(diào)查結論.

1.2?關鍵詞分布

通過對文獻關鍵詞的統(tǒng)計分析（有些文獻資料未寫明關鍵詞，則根據(jù)摘要與文章內(nèi)容提取關鍵詞），可將研究主要分為代數(shù)推理的理論研究、代數(shù)推理的認知分析以及代數(shù)推理的發(fā)展策略三個部分.代數(shù)推理的理論研究中，以對算術與代數(shù)的基本了解為基礎，進一步區(qū)分算術思維與代數(shù)思維（算術推理與代數(shù)推理），并提出“早期代數(shù)”的想法.代數(shù)推理的認知分析中，可以將關鍵詞歸為認知內(nèi)容、認知層次和認知困境三類.認知內(nèi)容方面，“概念理解”“概念教學”“乘法思維”“方程”“代數(shù)表達式”等詞出現(xiàn)頻次較高，是學生代數(shù)推理思考的重要部分.認知層次方面，主要是“評估”類研究，相對較少.認知困境主要體現(xiàn)在問題解決中不同類型問題的設置，語言表達方式和知識類型對學生理解并完成代數(shù)任務的影響.代數(shù)推理的發(fā)展策略中，主要關注教師在代數(shù)推理教學中所發(fā)揮的關鍵作用，兼顧教師的教學觀念、專業(yè)知識以及教學技能.

1.3?研究方法

教育研究主要包括理論研究、實證研究、實踐研究三種方法.其中，理論研究又可分為演繹研究（先驗推理論證）、歸納研究（經(jīng)驗推理論證）與類比研究；實證研究可分為歷史研究、調(diào)查研究與實驗研究，實證研究報告具有完整的問題假設、過程與方法、結果與討論；實踐研究主要表現(xiàn)為日常的教學經(jīng)驗總結和策略分析.

基于上述分類統(tǒng)計國外代數(shù)推理研究的研究方法，發(fā)現(xiàn)其以實證研究為主（82篇），其次是理論研究（16篇）和實踐研究（4篇）.實證研究大多基于已有研究成果的基本觀點進一步分析測試結果與訪談記錄，其中以定性研究居多，因為代數(shù)推理相比算術推理更具動態(tài)性，需要對學生的概念理解、程序技能及問題解決展開連續(xù)的觀察.另外，實驗研究也是關注代數(shù)推理能力動態(tài)發(fā)展的重要研究方法，尤其在培養(yǎng)教師代數(shù)推理教學能力的過程中，研究往往通過課程干預的方式，發(fā)展教師的“教學敏感性”.

2?研究內(nèi)容

根據(jù)前述對關鍵詞分析所確定的三大研究內(nèi)容，下面將作具體分析.

2.1?代數(shù)推理的理論研究

與國內(nèi)研究從邏輯學角度出發(fā)理解代數(shù)推理不同，國外研究者多從代數(shù)意義進行理解，因此在探究代數(shù)推理的本質(zhì)意義之前，對算術與代數(shù)的基本理解在研究中受到重視，而且由此可發(fā)現(xiàn)算術思維與代數(shù)思維的密切聯(lián)系.

2.1.1?算術與代數(shù)的區(qū)別與聯(lián)系

算術的基本對象是數(shù)，包括數(shù)的認識與數(shù)的運算等，而代數(shù)的基本對象除了數(shù)以外，還有更具廣泛意義的符號，主要體現(xiàn)為數(shù)的關系.出于代數(shù)的本體意義和功能意義兩種不同的視角，研究者對代數(shù)的理解有所不同（詳見表1）.本體意義上，代數(shù)主要包括算術的一般化、關系、結構、函數(shù)、模型等；功能意義上，代數(shù)主要在概括描述、規(guī)則操作、問題解決程序中體現(xiàn)出特殊的代數(shù)思想和方法.以上雖有不同，但這些理解也體現(xiàn)出，從算術到代數(shù)的學習，表現(xiàn)為從具體到一般的運算，而且學生在代數(shù)學習過程中也更要懂得代數(shù)的符號化、形式化、結構化與操作化的特點.

要說清算術與代數(shù)的區(qū)別是相對較難的.從符號意義來看，算術與代數(shù)存在許多相同的符號，但意義卻大相徑庭，比如對“等號”的理解是計算結果還是等價關系、對“字符”的理解是傳統(tǒng)的未知數(shù)還是任意一個數(shù)；從解題活動來看，算術是面向解決問題的答案，而非解決問題本身，代數(shù)的解題活動重在發(fā)現(xiàn)關系，操作代數(shù)規(guī)則[6]328.由此可知，兒童在算術中對“符號”“關系”“關系的轉換”的理解，可能會影響代數(shù)學習，因為算術與代數(shù)是緊密聯(lián)系的.兩者的聯(lián)系可以用數(shù)學概念的二重性理論解釋.抽象數(shù)學符號必須基于兩種不同的方法來思考，一是結構性（視為對象），二是操作性（視為過程），而算術與代數(shù)之間的聯(lián)系，就需經(jīng)歷操作—結構（過程—對象）的轉換，包括內(nèi)化、壓縮與客體化的過程，代數(shù)思維與代數(shù)推理體現(xiàn)其中[7]，需要將概念理解、程序技能和解決問題的能力融入學生的早期學習經(jīng)驗[8].

2.1.2?算術思維與代數(shù)思維的區(qū)別與聯(lián)系

算術思維注重利用數(shù)量的計算得出結果，聯(lián)結題目與答案，這個過程是程序性的、含情境的，具有特殊性、計算性的特點；而代數(shù)思維倚重的是關系的符號化及其運算，聯(lián)結量與量之間的關系，這個運算是結構性的、去情境的，具有一般性、形式化的特點[6]327.在算術思維到代數(shù)思維的過渡中，兩者可能基于同一套符號體系，是轉換的基礎，但是需意識到兩者對符號的解釋有所不同，對符號的使用也存在不同的操作，更涉及觀念的轉變.

具體而言，代數(shù)思維的特征主要包括五個方面.首先，代數(shù)思維的核心是一般化的思想.Kaput認為“代數(shù)是算術推理和定量推理的一般化，代數(shù)是一種句法導向的形式操作”是代數(shù)最關鍵的基本特征，代數(shù)思維體現(xiàn)一般化與形式化[2]4；Harel和Tall進一步指明代數(shù)的一般化主要有擴展性一般化、重構性一般化與分離性一般化三種類型[9].其次，代數(shù)思維是一種形式的符號操作，“成功地操作代數(shù)符號的能力要求我們首先能理解數(shù)學運算和關系的結構屬性……代數(shù)表征和符號操作的本質(zhì)特征是它應該來自于對語義或它所指意義的理解”[10].第三，代數(shù)思維是一種基于規(guī)則的推理，“代數(shù)是一種句法導向的形式操作，此種句法是指代數(shù)規(guī)則”[3]10.第四，代數(shù)思維是一種建模活動，在代數(shù)思維中可通過模式反映對象之間的某種規(guī)律，Berlin等人認為，從模式入手的課程能夠提升學生的思考與理解能力，學生需要從實際情境中選取素材，轉化為數(shù)學問題，再回到實際情境以評價結果，從而提升數(shù)學的真實感[11].最后，代數(shù)思維是多種推理能力的重要預測指標.有研究指出代數(shù)思維的多面性及其與認知能力的關系，除了類比和歸納等推理形式外，空間推理也是學生代數(shù)思維能力的重要預測指標[12].代數(shù)思維的以上五個特征，就一般思維的意義而言，學生將發(fā)展抽象概括、概念理解、理性分析、聯(lián)系實踐和推理能力的思考方法.

在目前的代數(shù)推理研究中，基本確定“代數(shù)推理是一個過程，學生通過這種過程來尋找某些數(shù)學問題或情境的模式，在數(shù)量之間建立關系，并通過形式化的象征表征和操縱來進行概括”[13].

2.2?代數(shù)推理的認知分析

基于對算術與代數(shù)、算術思維與代數(shù)思維的分析，許多研究者繼而關注學生在代數(shù)推理方面的認知情況.實際上，教師不僅要提供數(shù)學材料，還應了解學生如何學習數(shù)學，即他們的認知過程（包括認知內(nèi)容、認知層次、認知困境）[14]，所以關注這方面的研究很重要.

2.2.1?認知內(nèi)容

在確定代數(shù)推理的認知內(nèi)容時，研究者多關注學生的學習進程或軌跡，提出了代數(shù)的“大概念”以及相應的“核心概念”，并以此作為代數(shù)思維實踐的教學任務序列.“大概念”主要有：等價、表達式、方程和不等式；廣義算術；泛函思維；變量；比例推理[15].譬如，“喬治亞數(shù)學與科學行動”（Georgia Initiative in Mathematics and Science，簡稱GIMS），按照學段給出了代數(shù)的“Big Ideas”（大概念），每階段代數(shù)推理學習的核心思想保持一致，本質(zhì)上都是理解一般化、關系、結構，區(qū)別在于認知對象范圍的擴大以及認知階段目標的發(fā)展[6]310.結合其他研究來看，代數(shù)推理內(nèi)容的學習主要以理解等價關系和乘法思維、發(fā)現(xiàn)乘法推理與加法推理的區(qū)別為主，這可能是因為等價關系是代數(shù)結構進行轉化的依據(jù)，而乘法是理解其他運算規(guī)律的基本概念.熟悉以上代數(shù)課程的基本內(nèi)容，可以更好地建立起小學與初中代數(shù)內(nèi)容的聯(lián)系，算術與代數(shù)并非完全割裂的兩部分，如何在算術中教代數(shù)，體現(xiàn)了對代數(shù)思維及代數(shù)推理的關注.

一些研究者從代數(shù)推理能力的要求出發(fā)，結合完整的代數(shù)推理過程確定認知內(nèi)容.Harper在調(diào)查研究中業(yè)已證實學生在代數(shù)學習時，對一些問題的回答依次對應每一階段的代數(shù)方法，即“修辭代數(shù)——半符號代數(shù)——符號代數(shù)”[16].有研究者提出“戰(zhàn)略代數(shù)推理”的概念，關注學生的戰(zhàn)略能力及自適應推理，并提出五大能力的代數(shù)學習內(nèi)容：閱讀和解釋文本，理解問題陳述中的故事情節(jié)（背景）；確定數(shù)量和它們之間的關系（識別數(shù)量、發(fā)現(xiàn)關系）；使用數(shù)量之間關系的代數(shù)表示（生成表示、解釋表示）；精確執(zhí)行計算和程序并檢查結果的合理性；提供令人信服的解釋[17].Sarah R. Powell在研究中概括了代數(shù)推理過程所涉及的三種不同活動：代表性的——學生將口頭信息翻譯成符號表達式和方程式，還努力理解數(shù)學概念、運算和關系的概念基礎；變革性的——學生學習基于規(guī)則的活動，例如因式分解、擴展、替換、求解方程和簡化表達式；概括和證明——學生學習解決問題、建模、注釋結構、證明和預測[10]327.以上內(nèi)容也基本概括了多數(shù)研究中代數(shù)推理測試或代數(shù)推理教學的過程，代數(shù)推理支持學生有機會掌握一種代數(shù)的方法來解決問題，在證明推理、使用多種表示的過程中識別結構和關系.

2.2.2?認知層次

大型測評項目中的研究者傾向于選擇構建金字塔評價模型來測評代數(shù)推理的認知層次，譬如，美國國家數(shù)學科學教育研究中心開展的基于情境中的數(shù)學的評價項目（MIC）[19]，但是這類模型對代數(shù)的內(nèi)容細化不夠，不足以充分反映代數(shù)推理的特征.還有研究者使用SOLO模型，將代數(shù)學習的四個重要方面（一般特征、模式、表征、變量）與SOLO模型中的四個水平（前結構、單結構、多結構、關系）相結合，最終確定學生代數(shù)推理學習的具體表現(xiàn)，但是，同一個問題情境中往往不止體現(xiàn)代數(shù)學習的一個方面，代數(shù)推理能力的層次應該也體現(xiàn)在多個代數(shù)概念的聯(lián)結水平中.此外，澳大利亞RMF Ⅱ項目根據(jù)Rasch分析創(chuàng)建的項目層次結構確定了八個區(qū)域來假設學生的學習進程，學生行為的描述源于對每個區(qū)域內(nèi)項目的認知需求的考慮[20].這種方式既能細化代數(shù)內(nèi)容，確定代數(shù)推理的核心概念，又能基于核心概念的學習進展給出每一階段的層次水平，有助于學習者識別出自己在代數(shù)推理學習進程中的位置，并基于即時的學習體驗，在下一步的學習中找到聯(lián)系.

2.2.3?認知困境

研究者多通過問卷測試與訪談來分析并比較結果，從而發(fā)現(xiàn)導致學生在代數(shù)推理上存在差異的因素，進而判斷其認知困境.從學生自身來說，年齡、性別以及認知風格等方面都是可能的影響因素，所以學生的學習模式應該有所不同[21].從代數(shù)問題的設置來說，問題的難易程度、問題的類型、未知數(shù)量在問題中的位置、問題的語言表達以及有趣的問題情境等都會影響代數(shù)推理的進行[22][3]169.解題過程還會受到知識遷移、計算技巧的掌握、問題的求解策略等方面的影響[23][24].究其根本，主要是學生對代數(shù)的抽象性和形式化不適應，不能熟練運用代數(shù)的符號表征系統(tǒng)和形式規(guī)則，數(shù)學符號的學習還存在口語挑戰(zhàn)、閱讀挑戰(zhàn)及書寫困難，需要在學習過程中激發(fā)學生的學習動機，體會符號表達的重要性[6]339.再者，需要注意的是學生在代數(shù)推理過程中，最困難的是對代數(shù)結構的理解.代數(shù)結構的出現(xiàn)，對習慣于完成具體化操作的大多數(shù)學生而言是比較陌生的，因為他們無法觀察整體對象，如解方程時使用逆運算而非先觀察到方程的整體平衡關系.

2.3?代數(shù)推理的發(fā)展策略

以上代數(shù)推理認知維度的分析，表明了發(fā)展代數(shù)推理需要遵循學科的發(fā)展規(guī)律、學生的認知規(guī)律以及教學規(guī)律，因此在發(fā)展代數(shù)推理的過程中，“早期代數(shù)”、教師專業(yè)發(fā)展、教學策略的提出可能有助于學生獲得較好的代數(shù)推理學習效果.

2.3.1?“早期代數(shù)”

經(jīng)過一定訓練的學生要明顯比沒有提前滲透代數(shù)內(nèi)容和思想的學生能更合理地進行推理，而在小學算術教學中有效滲透代數(shù)推理是“早期代數(shù)”研究的主要觀點，并在相關研究項目中得以證實[25].在“早期代數(shù)”中滲透代數(shù)推理，美國研究者建議教師可以利用四則運算中的逆運算和重復運算，在小學課堂的算術推理中使用多種表征方式[26]；澳大利亞在小學階段的計算教學中提到了一種“皮特的算法”，是指在計算“32-5”這一等式時，不是直接計算得出答案，而是使用像“32+5-10”這樣的步驟來學習知識和培養(yǎng)推理能力[27]；新西蘭通過“學生數(shù)字運算的代數(shù)性質(zhì)”的研究，給出像“47+25=47+3+25-3=50+22”這樣的算式例子，體現(xiàn)出學生對數(shù)字間一般化關系的理解，不依靠字母或符號也可以實現(xiàn)一般化的策略，這種方法也被表示為“準變量表達式”[28].不管是可逆性變換，還是借用多種語用表達或外部模型，都體現(xiàn)出教學支架的作用，可以幫助學生降低代數(shù)推理的學習難度.

2.3.2?教師專業(yè)發(fā)展

國外研究非常重視教師在代數(shù)教學過程中的影響，認為教師應改變對代數(shù)的看法和教學方式，并關注學生對學習的看法[29].因此，代數(shù)推理的教學應該關注學生、教師與課程的整體聯(lián)系.基于Bair和Rich構建的數(shù)學教學知識框架[30]，對職前或在職教師的代數(shù)推理教學能力分析中，都會從教學內(nèi)容知識與學科關鍵知識出發(fā)進行專業(yè)發(fā)展干預，教師在代數(shù)推理教學實踐中，需要經(jīng)歷“對代數(shù)概念的認識與關注——制定修改任務——開發(fā)課堂實踐提供推理機會——開發(fā)數(shù)學實踐支持代數(shù)推理”四個階段[31].除了對代數(shù)推理教學提出要求，多數(shù)研究中提及元認知指導以幫助教師更好地把握課堂.有研究者提出教師可通過自我提問來思考數(shù)學步驟，調(diào)節(jié)自身學習的能力，這會反過來影響代數(shù)推理.具體表現(xiàn)為：知道該做什么（理解問題）；尋找全局（聯(lián)系問題）；知道如何、何時和為什么做（戰(zhàn)略問題）；監(jiān)測和評價這一進程（反思問題）[32].總之，既要關注對教師適應知識內(nèi)容的有效性進行分析與評估，又要通過提升教師的自我調(diào)節(jié)，優(yōu)化學生對學習過程的參與.

2.3.3?教學策略

在代數(shù)推理的教與學過程中，研究者會從學習心理的角度，為增強學生的代數(shù)推理能力，提供一些教學建議.首先是確保學生具備學習新數(shù)學策略所必需的先驗知識，在建模時教師可以使用“大聲思考”的技巧指導學生具體的技能[3]186.其次，研究者發(fā)現(xiàn)學生構建知識的類型和他們形成的模式之間存在一定的聯(lián)系，學生通過使用這些模式對口頭表述和符號表征之間的關系進行識別和擴展[33]，圖式策略有助于學生建構完整知識結構，促進其用結構和模型的思想來解決代數(shù)推理問題.第三，培養(yǎng)學生的符號意識，代數(shù)推理需要學生實現(xiàn)具體問題情境與關系表達的轉化，符號意識體現(xiàn)的也是學生進行分析、概括與推理的代數(shù)方法.第四，多元表征，即“文字的、表格的、圖形的和符號的以及各種表征之間的靈活轉換”[34]，能夠讓學生根據(jù)具體的代數(shù)內(nèi)容或自己的操作能力進行恰當?shù)倪x擇，有助于理解數(shù)學符號和抽象方程在具體層面上的運行，尤其對小學生有益.最后，可以實施分階段的漸進式教學，包括從具體到抽象的解釋，從簡單到復雜的問題的例子，或是始于簡單概念的教學[14]101.

綜上可見，在早期代數(shù)中，因為學生的數(shù)學思維習慣尚不完善，教師在代數(shù)推理教學中發(fā)揮著關鍵的引領作用，但是，仍需學生在代數(shù)推理教學中積極進行數(shù)學思考，尤其要營造課堂“推測”氛圍.因此，代數(shù)推理教學，是一個充分交流、展示、互動的教學過程.

3?結論與討論

綜合以上國外中小學代數(shù)推理研究的文獻分析，對國外研究的主要成果作如下總結，并結合我國研究現(xiàn)狀提出幾點啟示.

3.1?基本結論

首先，國外代數(shù)推理研究相對較為成熟，理論與實證研究相得益彰.對算術與代數(shù)、算術思維與代數(shù)思維的辨析與比較，是理解代數(shù)推理的奠基石；代數(shù)思維和代數(shù)推理的認知分析與發(fā)展策略，則指向理論到實踐的過渡，最終是要發(fā)展中小學生的代數(shù)思維和代數(shù)推理能力，這是代數(shù)教學的發(fā)展目標與方向.

其次，從研究對象與研究方法來看，研究者比較關注“早期代數(shù)”的影響，因此，對小學階段的代數(shù)思維和代數(shù)推理發(fā)展有較多的實證研究，用實驗數(shù)據(jù)論證觀點.

再者，從研究結果的預期發(fā)展而言，國外的代數(shù)思維與代數(shù)推理研究能夠較好地用于教學實踐，美國、俄羅斯、澳大利亞、新西蘭等國家都有相應的教育報告或研究項目來支持中小學校中代數(shù)課程的發(fā)展，給予數(shù)學教師專業(yè)發(fā)展的培訓機會，也促進學生在代數(shù)思維和代數(shù)推理方面的提升.最后，在研究基礎上，國外的代數(shù)推理研究相對而言較為重視對學習心理學的研究成果的借鑒，代數(shù)推理教學的發(fā)展策略也離不開對學生心理的分析.

3.2?研究討論

與國外相比，我國的代數(shù)推理研究還比較少，在理論與實踐的相互支持以及教師專業(yè)發(fā)展上都有所欠缺.我國代數(shù)推理研究具體可從以下幾個方面做出努力.

3.2.1?把握算術與代數(shù)、算術思維與代數(shù)思維的本質(zhì)區(qū)別與聯(lián)系

雖然有不少研究者明確提出“在算術中教代數(shù)”或者“從算術思維過渡到代數(shù)思維”，但在理解算術與代數(shù)、算術思維與代數(shù)思維時，會局限于體會數(shù)與符號的區(qū)別、程序與結構的區(qū)別，教師仍需有意識地將區(qū)別與內(nèi)容聯(lián)系起來，具體地就一般化、結構、關系、函數(shù)、變化、模型、問題解決等做出細致辨別，由此，或許能對每一部分的內(nèi)容提出發(fā)展目標，并在算術與代數(shù)中找到相對應的聯(lián)系.

3.2.2?要在問題解決中找到代數(shù)推理任務設計的思考性與連貫性

根據(jù)已有研究，代數(shù)推理任務設計有兩個基本條件，一是問題解決的重點不在于得到事實性的答案，而是關注學生展開關系轉化的思考過程；二是問題解決的情境創(chuàng)設，可以是生活情境，聯(lián)系學生的生活經(jīng)驗，更要呈現(xiàn)數(shù)學情境，使學生能夠?qū)W會觀察、想象、描述與概括.在中小學數(shù)學課程安排上，我國主要是以“數(shù)與代數(shù)”作為一個課程領域，數(shù)與運算、數(shù)量關系、數(shù)與式、方程與不等式、函數(shù)等內(nèi)容進行交叉學習，如何保持代數(shù)內(nèi)容的連貫性以及與算術內(nèi)容的聯(lián)系，是需要考慮的問題.而且，在我國課程標準中可發(fā)現(xiàn)，數(shù)學推理主要強調(diào)合情推理與演繹推理能力的發(fā)展，對代數(shù)推理任務的設計也要遵循一般推理的規(guī)范.因此，為了在“數(shù)與代數(shù)”中促進學生代數(shù)推理能力的發(fā)展，任務設計需要兼顧學生認知特點、代數(shù)知識特征、一般推理規(guī)范三個方面，以滿足學生展開任務過程的心理邏輯與知識邏輯.

3.2.3?關注教師代數(shù)教學內(nèi)容知識的專業(yè)發(fā)展

一方面，考慮到過去常常以學生的測試成績作為評估教師教學的標準，在代數(shù)推理教學中，學生與教師的評估方式和內(nèi)容都應發(fā)生改變.代數(shù)推理作為一種思維方式，更多地表現(xiàn)為教師與學生的思考能力，而且代數(shù)推理中“關系的轉換”需要過程性的記錄，因此以定性描述來給予教師專業(yè)素養(yǎng)的判定是必要的.另一方面，基于社會文化的視角，代數(shù)推理教學應該是一種集體實踐，教師與學生都要參與思考過程，教師才能依據(jù)對學生的“說理”過程進行思維判斷，抓住代數(shù)推理引導的契機.這對教師而言，既要考慮其教學專業(yè)素養(yǎng)的培養(yǎng)，也對其代數(shù)推理專業(yè)內(nèi)容知識的學習提出嚴格要求.

總之，國外中小學代數(shù)推理研究已經(jīng)獲得了較豐富的成果，并且關注到了早期階段代數(shù)推理能力的培養(yǎng)，其研究關注點和研究方法等都可以為我國相關研究提供借鑒與啟發(fā).

參考文獻

[1]Kieran， C.. Learning and Teaching Mathematics[J]. Psychology Press Lid， 1997 （3）： 136-137.

[2]Kaput， J.. Transforming Algebra from an Engine of Inequity to an Engine of Mathematical Power by “Algebrafying” the K-12 Curriculum[C]// National Council of Teachers of Mathematics & Mathematical Sciences Education Board （Eds.）. The Nature and role of algebra in the K-14 curriculum： Proceedings of a National Symposium. Washington， DC： National Research Council， National Academy Press， 1998： 25-26.

[3]Koedinger， N. K. R.. Teachers＼＼" and researchers＼＼" beliefs about the development of algebraic reasoning[J]. Journal for Research in Mathematics Education， 2000， 31（2）： 168-190.

[4]?全美數(shù)學理事會. 美國學校數(shù)學教育的原則和標準[M]. 蔡金法譯. 北京：人民教育出版社，2004：73.

[5]?Godino， J. D.， Castro， W. F.， Ake， L. P.， & Wilhelmi， M. R.. The Nature of Elementary Algebraic Reasoning[J]. Bolema-Mathematics Education Bulletin-boletim De Educacao Matematica， 2012， 26（42B）： 483-511.

[6]鮑建生，周超著. 數(shù)學學習的心理基礎與過程[M]. 上海：上海教育出版社，2009：310-339.

[7]?Anna Sfard. On the dual nature of mathematical conceptions： reflections on process and objects as different sides of the same coin[J]. Educational Studies in Mathematics， 1991， 22（1）： 1-36.

[8]Glassmeyer， D.， & Edwards， B.. How middle grade teachers think about algebraic reasoning[J]. Mathematics Teacher Education & Development， 2016， 18（2）： 92-106.

[9]?Tall， H. D.. The general， the abstract， and the generic in advanced mathematics[J]. For the Learning of Mathematics， 1991， 11（1）： 38-42.

[10]?Booth， G.. Dynamic representation and the development of a process understanding of function Research[J]. Issues in the Learning and Teaching of Algebra， 1988， 4（3）： 11-15.

[11]?Berlin， D. F.， & Hillen， J. A.. Making connections in math and science： identifying student outcomes[J]. School Science and Mathematics， 1994， 94（6）： 283-290.

[12]?Pitta-Pantazi D.， Chimoni M.， Christou C.. Different types of algebraic thinking： an empirical study focusing on middle school students[J]. International Journal of Science and Mathematics Education， 2020， 18（5）： 965-984.

[13]Blanton， M.L.， & Kaput，J.J.， Elementary Grades Students' Capacity for Functional Thinking[J]. International Group For The Psychology Of Mathematics Education， 2004：136.

[14]Basir M A， Waluya S B. How Students Use Cognitive Structures to Process Information in the Algebraic Reasoning？[J]. How Students Use Cognitive Structures to Process Information in the Algebraic Reasoning？， 2022， 11（2）： 821-836.

[15]?Fonger， N. L.， Stephens， A.， Blanton， M.， & Knuth， E.. A Learning Progressions Approach to Early Algebra Research and Practice[C]. 37th annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education， 2015：201-204.

[16]?Harper， E.. Ghosts of Diophantus[J]. Educational Studies in Mathematics， 1987， 18（1）： 75-90.

[17]?Lepak， J. R.， Wernet， J. L. W.， & Ayieko， R. A.. Capturing and characterizing students strategic algebraic reasoning through cognitively demanding tasks with focus on representations[J]. The Journal of Mathematical Behavior， 2018， 50： 57-73.

[18]?Powell， S.R.， Mason， E.N.， Bos S E， et al. A Systematic Review of Mathematics Interventions for Middle‐School Students Experiencing Mathematics Difficulty[J]. Learning Disabilities Research And Practice， 2021， 36（4）：295-329.

[19]張春莉. 小學生數(shù)學能力評價研究[M]. 北京：人民教育出版社，2010：28-30.

[20]?Siemon， D.， Day， L.， Stephens， M.， Horne， M.， Callingham， R.， & Watson， J.. Reframing Mathematical Futures： Using Learning Progressions to Support Mathematical Thinking in the Middle Years. 40 years on： We are still learning！[C]// Proceedings of the 40th Annual Conference of the Mathematics Education Research Group of Australasia. Melbourne： MERGA， 2017： 651-654.

[21]?Indraswari， N. F.， Budayasa， I. K.， & Ekawati， R.. Algebraic reasoning in solving mathematical problem based on learning style[J]. Journal of Physics： Conference Series， 2018， 947： 012061.

[22]?Walkington， C.， Petrosino， A.， & Sherman， M.. Supporting algebraic reasoning through personalized story scenarios： how situational understanding mediates performance[J]. Mathematical Thinking & Learning， 2013， 15（2）： 89-120.

[23]?Powell， S. R.， & Fuchs， L. S.. Does early algebraic reasoning differ as a function of students difficulty with calculations versus word problems？[J]. Learning Disabilities Research & Practice， 2014， 29（3）： 106-116.

[24]?Ana， S.， Andreja， B.， Andrija， V.， & Maja， P.. Development of abstract mathematical reasoning： the case of algebra[J]. Frontiers in Human Neuroscience， 2014， 8： 679.

[25]?Carpenter， T. P. & Levi， L.. Developing conceptions of algebraic reasoning in the primary grades[C]. Paper presented at the Annual Meeting of American Educational Association， Montreal， Canada， 2000： 3.

[26]?Christine Ormond. Two key ways to establish some early algebraic ideas in primary classroom[J]. APMC， 2012 （17）： 13-18.

[27]章勤瓊，譚莉. 早期代數(shù)思維的培養(yǎng)：小學階段“數(shù)與代數(shù)”教學的應有之義[J]. 江蘇教育，2013（33）：7-9.

[28]張文宇，傅海倫. 新西蘭小學運算能力項目的影響及啟示[J]. 外國中小學教育，2010（05）：48-53.

[29]?Tunks， J.， & Weller， K.. Changing Practice， Changing Minds， from Arithmetical to Algebraic Thinking： An Application of the Concernsbased Adoption Model（CBAM）[J]. Educational Studies in Mathematics， 2009， 72（2）： 174.

[30]?Bair， S. L.， & Rich， B. S.. Characterizing the development of specialized mathematical content knowledge for teaching in algebraic reasoning and number theory[J]. Mathematical Thinking and Learning， 2011， 13（4）： 292-321.

[31]?Hunter， J.. Teacher actions to facilitate early algebraic reasoning[J]. Mathematics Education Research Group of Australasia， 2015：58-67.

[32]Kramarski， B.. Promoting teachers algebraic reasoning and self-regulation with metacognitive guidance[J]. Metacognition and Learning， 2008， 3（2）： 83-99.

[33]?Steele， D. F.， & Johanning， D. I.. A schematic“theoretic view of problem solving and development of algebraic thinking[J]. Educational Studies in Mathematics， 2004， 57（1）： 65-90.

[34]?Choike， J. R.. Teaching strategies for “algebra for all”[J]. The Mathematics Teacher， 2000， 93（7）： 556-560.

作者簡介?謝春艷（1996—），女，湖南邵東人，教育學碩士;主要從事數(shù)學教育研究.

黃娜娜（1996—），女，內(nèi)蒙古通遼人，碩士研究生;主要從事數(shù)學教育研究.

潘禹辰（1998—），女，江蘇蘇州人，碩士研究生;主要從事數(shù)學教育研究.

徐文彬（1966—），男，安徽宣城人，教授，博士生導師;主要從事數(shù)學教育研究.