基于ARIMA-LSTM的高速公路交通安全組合預測模型研究
梁乃興,閆 杰,楊文臣,曹源文,房 銳
(1. 重慶交通大學 土木工程學院,重慶400074;2. 云南省交通規劃設計研究院有限公司 陸地交通氣象災害防治技術國家工程實驗室,云南 昆明 6502001;3. 重慶交通大學 交通裝備與系統集成重慶市重點實驗室,重慶400074)
0 引 言
全球每年大約有124萬人死于交通事故,超過2 000萬人因事故受傷,若以此趨勢,2030年道路交通事故或將成為全球第7大死亡原因[1]。此外,高速公路的百公里事故率、百公里傷、亡率與普通公路相比將增加2.0倍、2.8倍、4.0倍[2]。因此,探索高速公路交通事故在時間維度上的分布規律,并建立具備良好預測能力的高速公路交通事故預測模型,主動研判交通事故態勢及源頭治理對策,一直是宏觀道路交通安全管理的重要問題。
道路交通事故預測已經從傳統的定性預測發展為定量預測,定量預測的模式又可分為基于因果關系和基于時空關系建模2種[3]。因果模型主要基于道路幾何特征、道路基礎設施、交通環境(交通量、大型車比例等)等影響因素與交通事故評價指標之間的邏輯關系進行建模,其代表性預測方法為邏輯回歸分析法。時空模型主要基于交通事故在時空維度上的分布規律進行建模,通過捕捉歷史事故數據中的時空特征規律,進行外延預測和安全調控。多數學者對交通事故因果關系模型進行了大量的研究,而對于高速公路時序交通事故預測研究相對較少,其主要預測方法包括時間序列法、馬爾科夫法、神經網絡法等。
經典的時間序列統計回歸模型最早應用于交通事故時空模型,J.KARTIKEYA等[4]對比分析了多種時間序列模型在印度交通工程中的應用及其局限性;張杰等[5]基于1970—1997年全國交通事故10萬人口死亡率數據建立自回歸差分移動平均(ARIMA)模型,該模型能較好擬合交通事故數據并具備良好的短期預測能力;C.CHUKWUTOO等[1]基于ARIMA與ARIMAX(帶回歸項的ARIMA)模型對尼日利亞阿南布拉州的道路交通事故進行了預測,表明引入外部變量的ARIMAX模型優于ARIMA模型;黃宇等[6]通過建立向量自回歸(VAR)模型對交通事故與經濟損失之間的關系進行了研究。經典時間序列模型大多建立在眾多前提與假設之上,實際應用中很多目標事件并不能完全滿足這些假設,限制了經典時序模型的預測效果。
近年來,系統工程和機器學習理論模型逐漸應用于交通事故時間序列預測。吳盧榮[7]運用聚類分析與馬爾科夫鏈建立了宏觀交通安全預測模型,預測了未來31個地區的交通安全趨勢;陳玉飛等[8]基于交通事故數據,建立了灰色關聯模型(GM),結果表明GM(1,5)模型優于GM(1,8);蔣艷輝[9]建立了基于指數平滑和馬爾科夫鏈的交通事故預測模型,用以預測交通事故造成的死亡人數;張志豪等[10]利用1997—2016年交通事故統計數據,分別建立了多元線性回歸、BP及LSTM神經網絡,發現LSTM模型預測結果最好。
為提高交通事故單一時序模型的預測精度,許多學者提出組合預測的方法。X.H.JIN等[11]建立了灰色馬爾科夫組合預測模型,其相對誤差低于灰色預測模型;G.REN等[12]等基于粒子群算法與SVR建立了事故預測模型,其結果優于BP模型;謝學斌等[13]基于ARIMA及XGBoost算法建立了組合預測模型,用于擬合1973—2010年全國交通事故統計數據;Z.H.ZHANG等[14]以1997—2016年全國交通事故死亡人數為基礎,建立了基于LSTM和梯度提升回歸樹(GBRT)的事故組合模型。研究表明,與單一模型相比,組合模型的預測能力和魯棒性均有所提升,是目前時序交通事故預測的主要方向。
LSTM神經網絡能夠有效逼近時序數據的不確定性和周期性,已在金融、交通流等多個領域取得好的應用效果,但其對樣本數據量要求較高。ARIMA模型可以較好擬合線性時序特征,提供先驗知識,但對非線性特征的捕捉能力弱,目前鮮有將ARIMA和LSTM組合并應用于交通事故預測方面的成果。因此,研究以重慶市11條高速公路交通事故數據為研究對象,分析交通事故總數和死亡人數的月分布規律,通過ARIMA時序統計模型和LSTM神經網絡分別擬合時序交通事故數據的線性和非線性特征,構建山區高速公路交通事故ARIMA-LSTM組合預測模型,可為高速公路主動交通安全管理和綜合治理提供參考。
1 方法模型
1.1 ARIMA模型
ARIMA (p,d,q) 模型是應用最為廣泛的一種時間序列預測方法[15],模型建立后可根據歷史值和當前值來預測未來值。基本建模流程為:首先檢驗時間序列平穩性,通過差分對非平穩序列進行平穩化處理,確定差分參數(d);其次通過觀察偏自相關(PACF)和自相關圖(ACF)確定自回歸參數(p)和移動平均參數(q),以此建立模型,如式(1)[16]:
(1)
式中:Φ(·)、Θ(·)分別代表p階自回歸系數多項式、q階移動平均系數多項式;d=(1-B)d為差分計算;B為延遲算子,且Bnxt=xt-n;{εt}為隨機誤差序列;E(·)、Var(·)分別為·的期望與方差。
1.2 LSTM模型
LSTM神經網絡是遞歸神經網絡(RNN)的一個變種,LSTM神經元的獨特結構很好的解決了長期依賴(時間步長很大)情況下,傳統RNN模型的梯度消失或爆炸等問題,使神經網絡模型具備傳遞較遠節點歷史信息的能力[17]。LSTM通過在遞歸神經網絡神經元結構中增添遺忘門、輸入門以及輸出門,不斷調整自循環中的的權重,當參數固定時,各時點的積分尺度可以動態浮動,從而規避梯度消失或爆炸問題,其示意如圖1[18]。
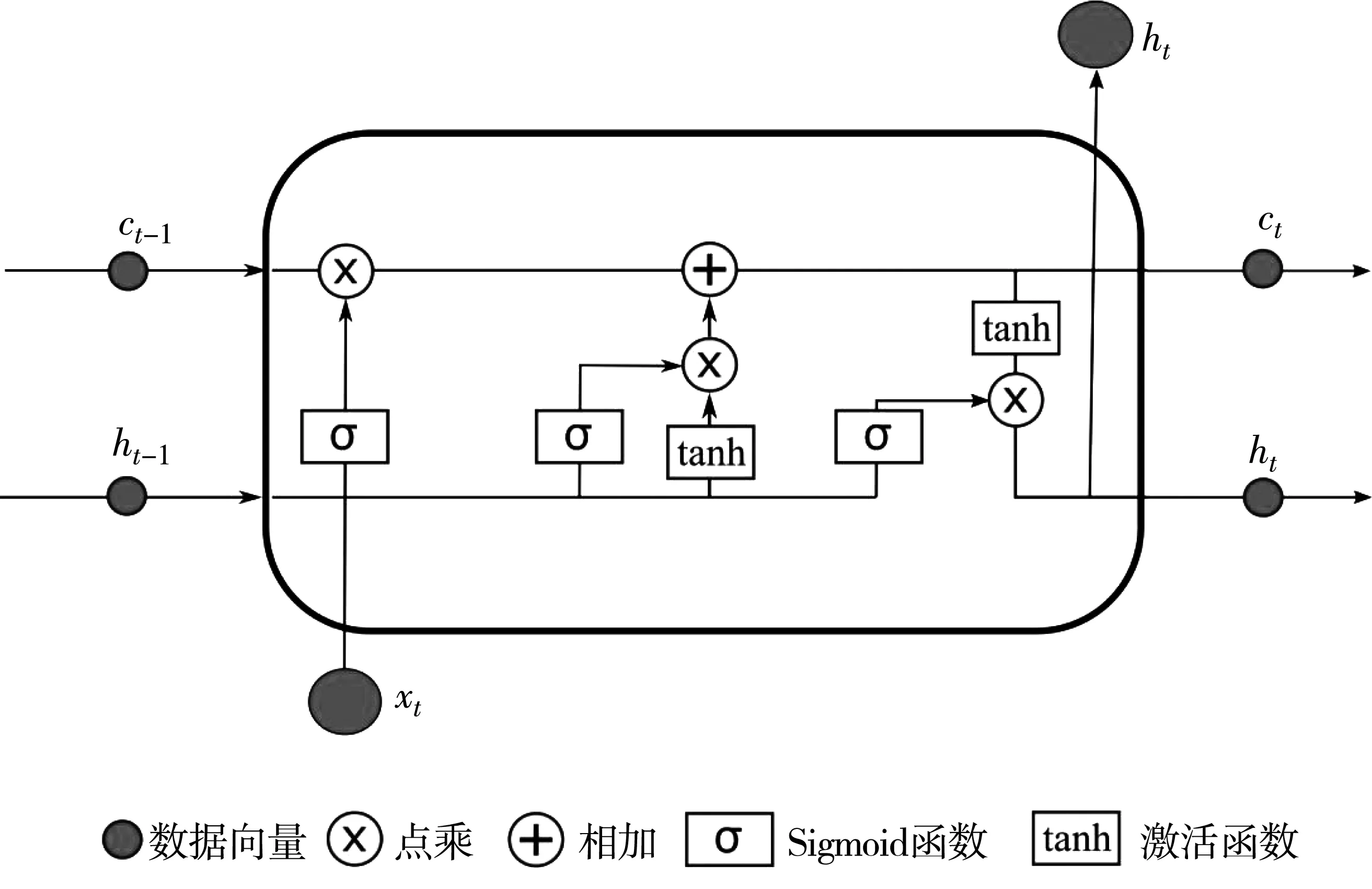
圖1 LSTM神經網絡示意Fig.1 Schematic diagram of LSTM neural network
假定時間步長為T′,LSTM神經網絡的輸入序列為X={x1,x2,…,xt,…,xT′}。圖1中xt為t時刻神經元的輸入,ht-1為上一神經元的輸出,ct-1為截止到上一時刻的神經元狀態。LSTM神經網絡基本公式如式(2)~式(6)[19]:
ft=σ(Wf×[ht-1,xt]+bf)
(2)
it=σ(Wi·[ht-1,xt]+bi)
(3)
(4)
ot=σ(Wo·[ht-1,xt]+bo)
(5)
ht=ot×tanh(Ct)
(6)
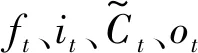
以t時刻為例,LSTM神經網絡首先通過遺忘門處理傳入t時刻的神經元狀態ct-1,舍棄無效信息,如式(2);然后通過式(3)、式(4)建立輸入門,根據上一時刻的輸出與當前時刻的輸入將神經元狀態更新為Ct。最后通過輸出門輸出Ct中的相關信息,此功能的實現如式(5)、式(6)。
1.3 ARIMA-LSTM組合模型
道路交通事故數據沿時間維度的分布既包含線性特征又包含非線性特征。ARIMA模型隸屬線性模型,只能擬合時間序列數據中的線性特征, LSTM神經網絡則可以彌補這一缺點[20]。先采用ARIMA模型對交通事故數據中的線形特征進行擬合預測,然后采用LSTM神經網絡模型對殘差序列中的非線性特征進行擬合,最后將二者進行線形組合得到組合模型最終值。具體建模步驟如下:
1) 整合、處理高速公路交通事故數據,將事故數據延時間維度展開,以單位根(ADF)法檢驗各序列的平穩性,采用差分、平滑等方法將非平穩序列轉為平穩序列。
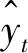
(7)
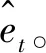
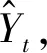
(8)
2 數據選取
2.1 數據來源
將重慶市包茂高速等11條高速公路2011—2016年共計65 131起交通事故數據為研究對象,由于事故數據不完整,將不完整的高速事故記錄剔除后,共使用65 119起交通事故數據用于構建交通事故月分布序列,事故統計信息如表1。將2016年8月1日前的序列數據作為模型的訓練集,將2016年8月1日及之后時刻的序列數據作為模型的測試集,訓練集樣本量約占全集的93%,測試集約占比7%。
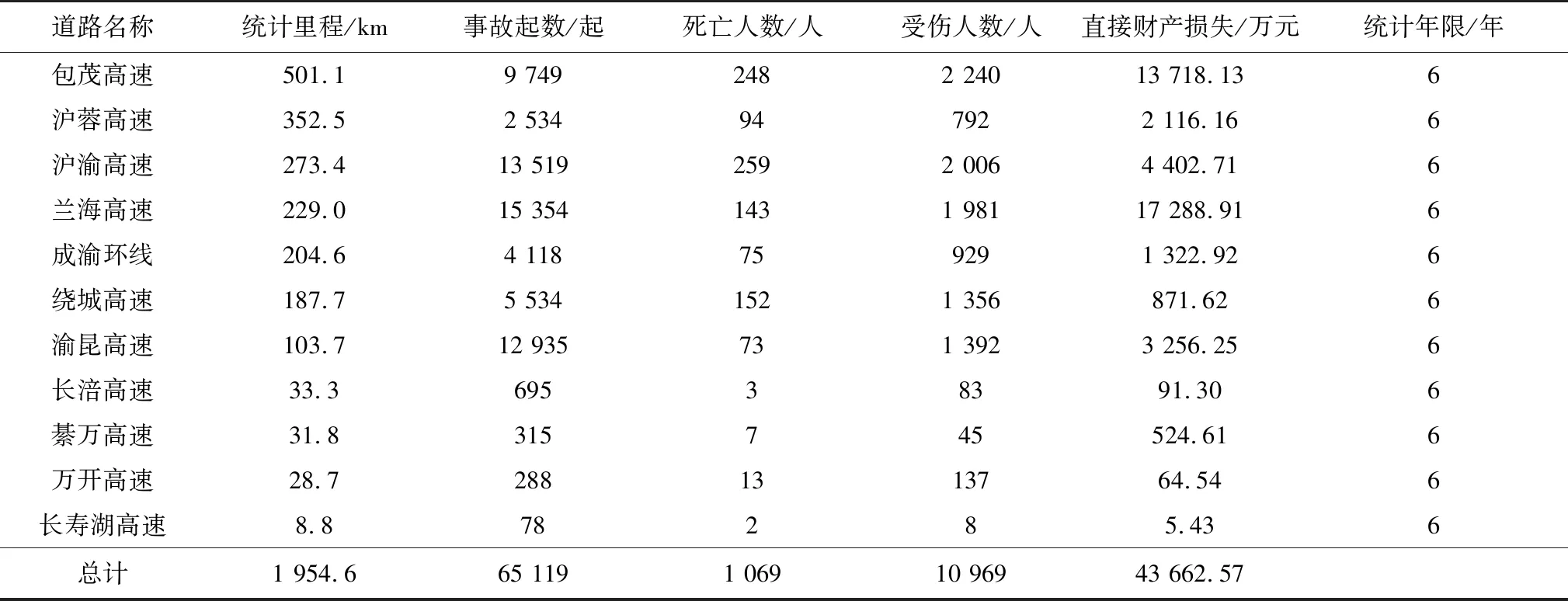
表1 2011—2016年11條高速公路交通事故統計
2.2 指標選取
道路交通事故的總量指標主要包括事故數量、死亡人數、受傷人數和財產損失4項。由于數據原因僅采用事故數量和死亡人數2項指標,時間以“月”為單位,將高速公路交通事故數據按各指標在時間維度展開,見圖2、圖3。

圖2 “事故數量”初始序列分布Fig.2 Initial sequence distribution of “number of accidents”
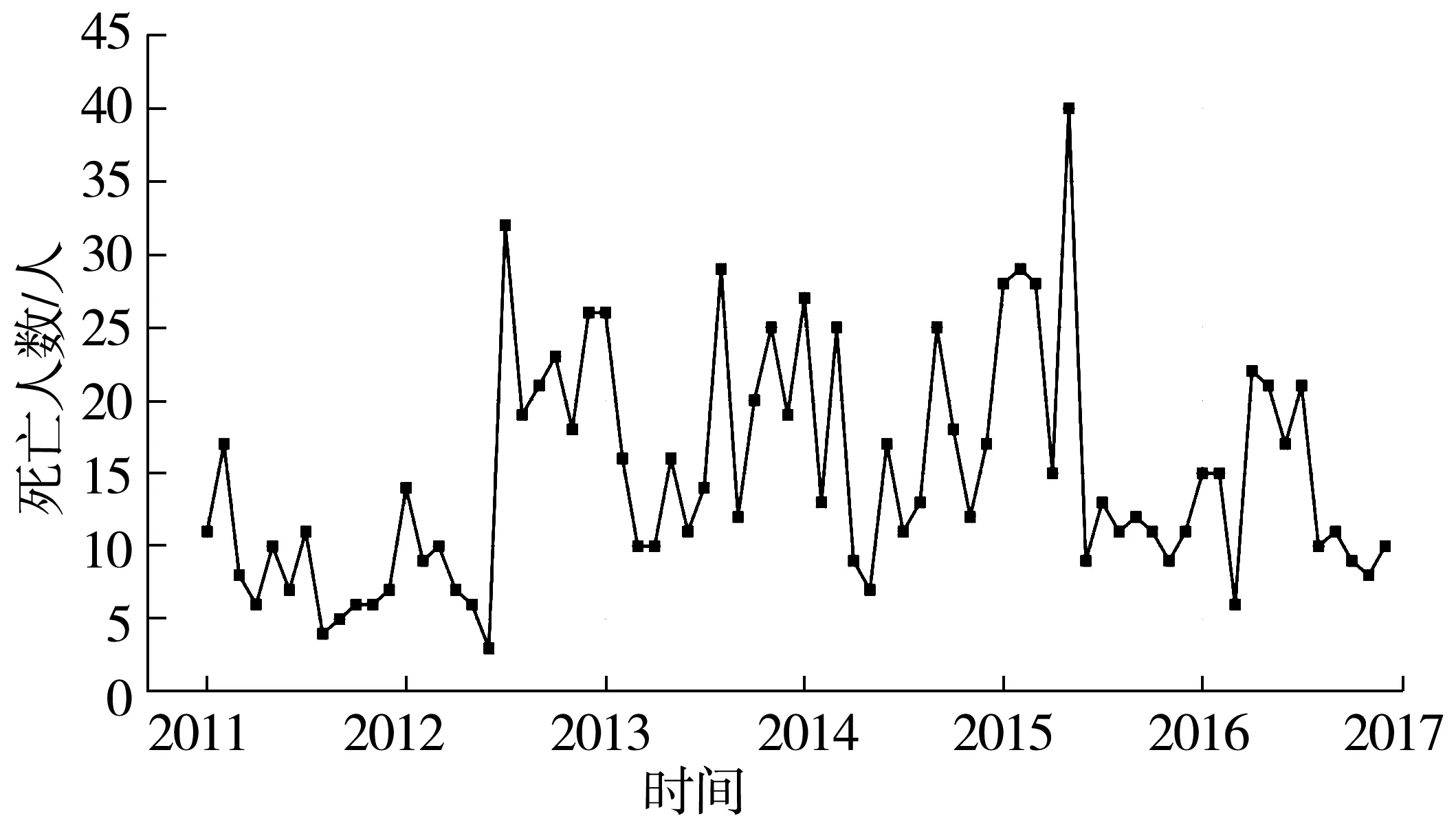
圖3 “死亡人數”初始序列分布Fig.3 Initial sequence distribution of “death toll”
此外,以均方根誤差(RMSE)以及平均絕對百分比誤差(MAPE)作為評價模型優劣的衡量指標。如式(9)、式(10):
(9)
(10)
式中:Ttotal為樣本總量,即總時間步長;ERMSE為均方根誤差;EMAPE為平均絕對百分比誤差。
3 實例分析
3.1 數據處理
ARIMA時間序列模型要求序列數據為平穩序列,因此建模之前首先檢驗序列數據的平穩性。采用ADF法分別檢驗“事故數量”與“死亡人數”初始序列,如表2。由表2可以看出“事故數量”初始序列的P值 >0.05且T值大于3個置信區間的臨界值,故“事故數量”序列為非平穩序列,該序列需要進一步平穩化處理。而“死亡人數”初始序列P值 <0.05,為平穩時間序列。
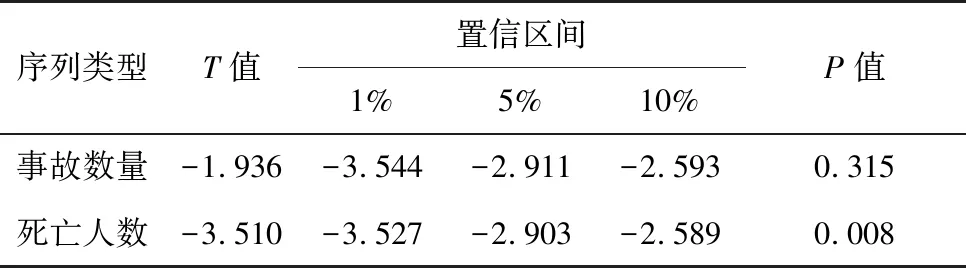
表2 初始序列ADF檢驗
由圖2可以看出“事故數量”初始序列振動幅度較大且呈“年”周期性變化。首先對該序列進行對數轉換,以減小序列數據的振動幅度;之后運用滑動窗口為12的移動平均方法剔除序列中的周期性因素;最后采用差分法將序列處理成為平穩時間序列,過程中分別采用ADF檢驗序列的平穩性,結果如表3。
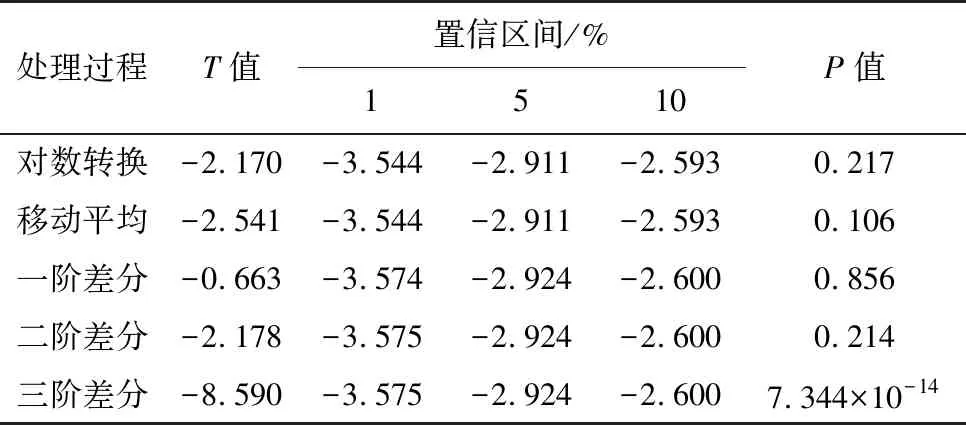
表3 “事故數量”序列ADF檢驗
3.2 ARIMA模型建立
通過處理后的平穩時間序列生成的偏自相關圖(PACF)與自相關圖(ACF)對ARIMA模型進行參數估計,如圖4、圖5,圖中灰色區域為置信區間。
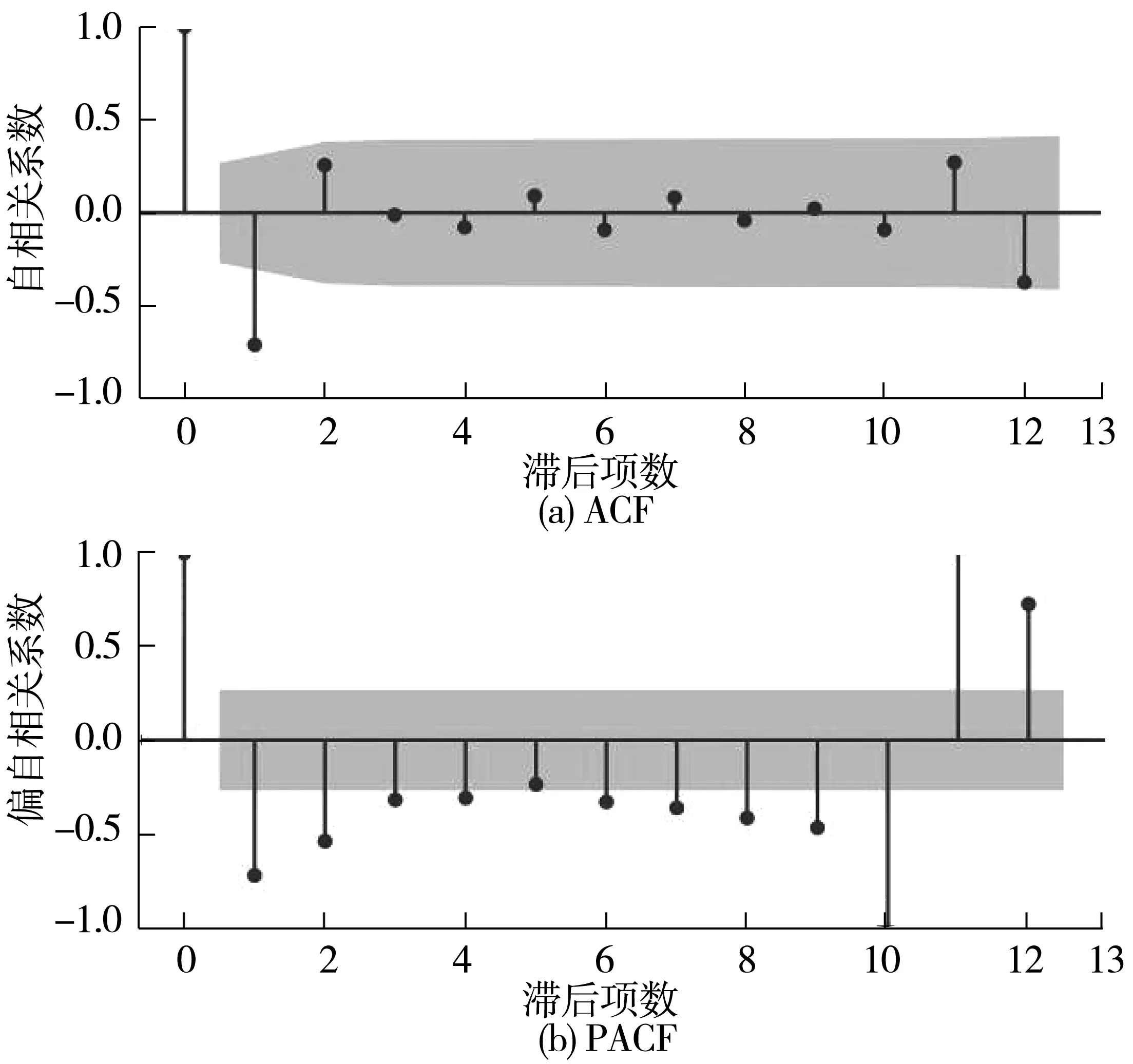
圖4 “事故數量”序列的ACF與PACFFig.4 ACF and PACF diagrams of the “number of accidents” sequence
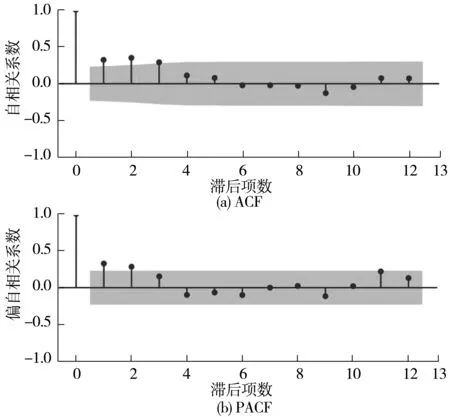
圖5 “死亡人數”序列的ACF與PACFFig.5 ACF and PACF diagrams of the “death toll” sequence
以“死亡人數”序列為例,其自相關系數為2階截尾,偏自相關圖呈拖尾狀況。故模型參數可以估計為ARIMA(0, 0, 2)、ARIMA(1, 0, 2)、ARIMA(1, 0, 1),3個模型進行試算后求出AIC值,分別為465.38、461.85、462.17。依據最小信息量原則,“死亡人數”指標的最佳模型為ARIMA(1, 0, 2)。同理,“事故數量”指標的最佳模型為ARIMA(1, 3, 2)。
“事故數量”和“死亡人數”序列的ARIMA模型預測結果如圖6,圖中豎直虛線用以區分樣本集,虛線左側為訓練集樣本,右側為測試集樣本。此外模型建立后還需要對模型的殘差序列進行正態性和自相關性檢驗,以確保模型的有效性。由圖7的正態性檢驗可以看出,殘差序列基本服從正態分布;同時對殘差進行D-W檢驗,“事故數量”模型的D-W檢驗值為2.31,“死亡人數”模型的D-W檢驗值為1.99。兩者的D-W檢驗值都接近2,模型滿足自相關檢驗。
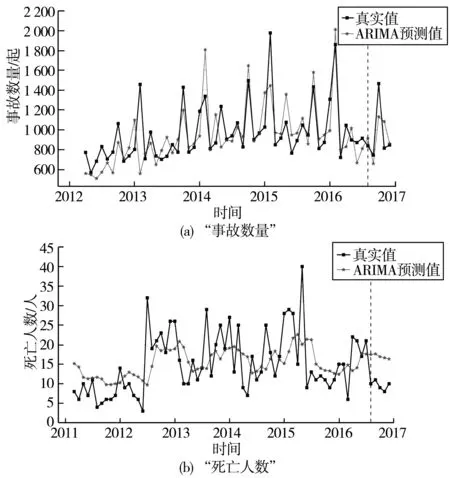
圖6 “事故數量”和“死亡人數”ARIMA模型預測Fig.6 “Number of accidents” and “death toll” ARIMA model prediction
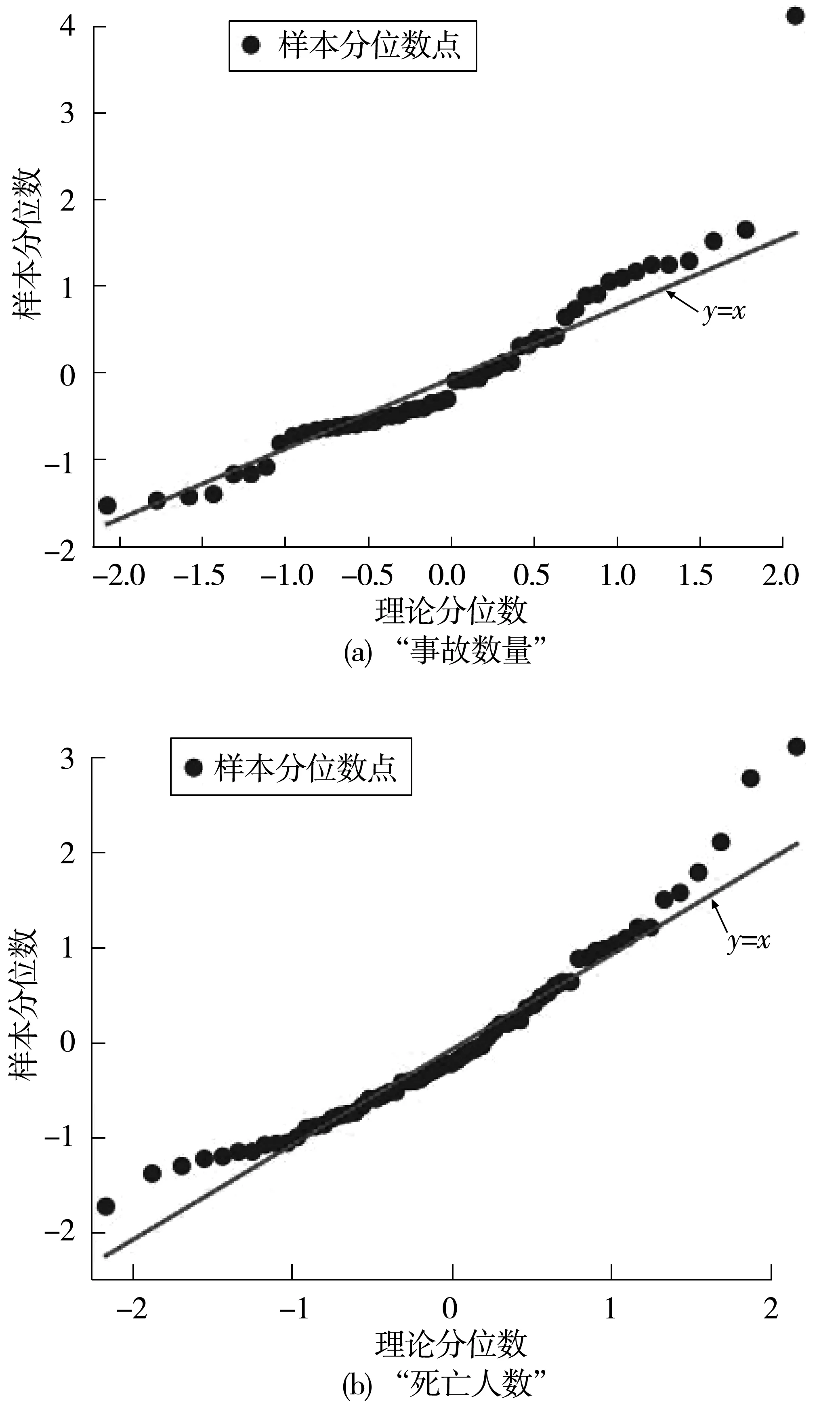
圖7 殘差QQ圖Fig.7 Residual QQ plot
由圖6可知,“事故數量”ARIMA模型的預測效果良好,比較接近初始序列數據的分布曲線,并能夠預測出該序列測試集數據的變化趨勢;“死亡人數”ARIMA模型對原始序列的擬合預測效果一般,存在一定的滯后性,并且隨著時間步長的增長,模型對于測試集的預測能力逐漸下降,無法準確預測出測試集的變化趨勢。
3.3 LSTM模型建立
基于Pytorch 1.7.1搭建LSTM神經網絡,分別根據“事故數量”和“死亡人數”ARIMA模型的殘差序列建立LSTM預測模型,旨在通過擬合訓練集中殘差序列的非線性時序特征,對測試集中的殘差進行預測,使組合模型獲得更優的預測效果。殘差序列的訓練集與測試集劃分同樣采用上述時間節點,以“死亡人數”LSTM模型為例,具體建模流程為:
1) 對序列進行歸一化,將數據壓縮到 [-1,1] 范圍內,以確保LSTM模型能夠快速收斂;
2) 對模型進行超參數選擇,經過反復對比發現,當殘差序列的時間步長為4時模型能很好地捕捉殘差序列中的非線性因素。經過反復調整,最終超參數選擇為:Adam優化器、學習率為0.001、batch_size = 1、神經網絡層數為1、神經元個數為45、迭代次數為140;
3) 最終模型輸出結果需要反歸一化,對數據進行還原。
模型預測結果如圖8,可以看出LSTM神經網絡模型能夠從殘差序列中提取一定的有效時序信息。
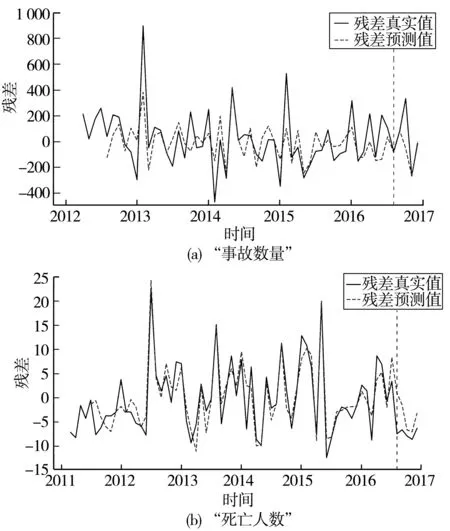
圖8 “事故數量”和“死亡人數”LSTM殘差預測Fig.8 “Number of accidents” and “death toll” LSTM residual prediction
3.4 ARIMA-LSTM組合模型建立
將ARIMA預測值與LSTM得到的殘差預測值依據式(8)進行線性組合,得到最終的組合模型預測值。“事故數量”和“死亡人數”指標的初始序列、ARIMA模型預測值以及組合模型預測值對比分析(圖9)。圖9中兩個指標的組合模型相較于單一的ARIMA模型都有很大的提升,更接近原始序列,并且組合模型能夠更好擬合預測出序列中的趨勢變化。然而,在每年2月和10月的事故數量和死亡人數峰值月份,組合模型的預測誤差仍較大,這是因為在春運和國慶節重大假日,這2個月的交通流量激增,交通事故的發生更為集中,加之研究節假日的樣本數量少,所構建的組合模型尚不能有效逼近事故數據的非時序特征所致。
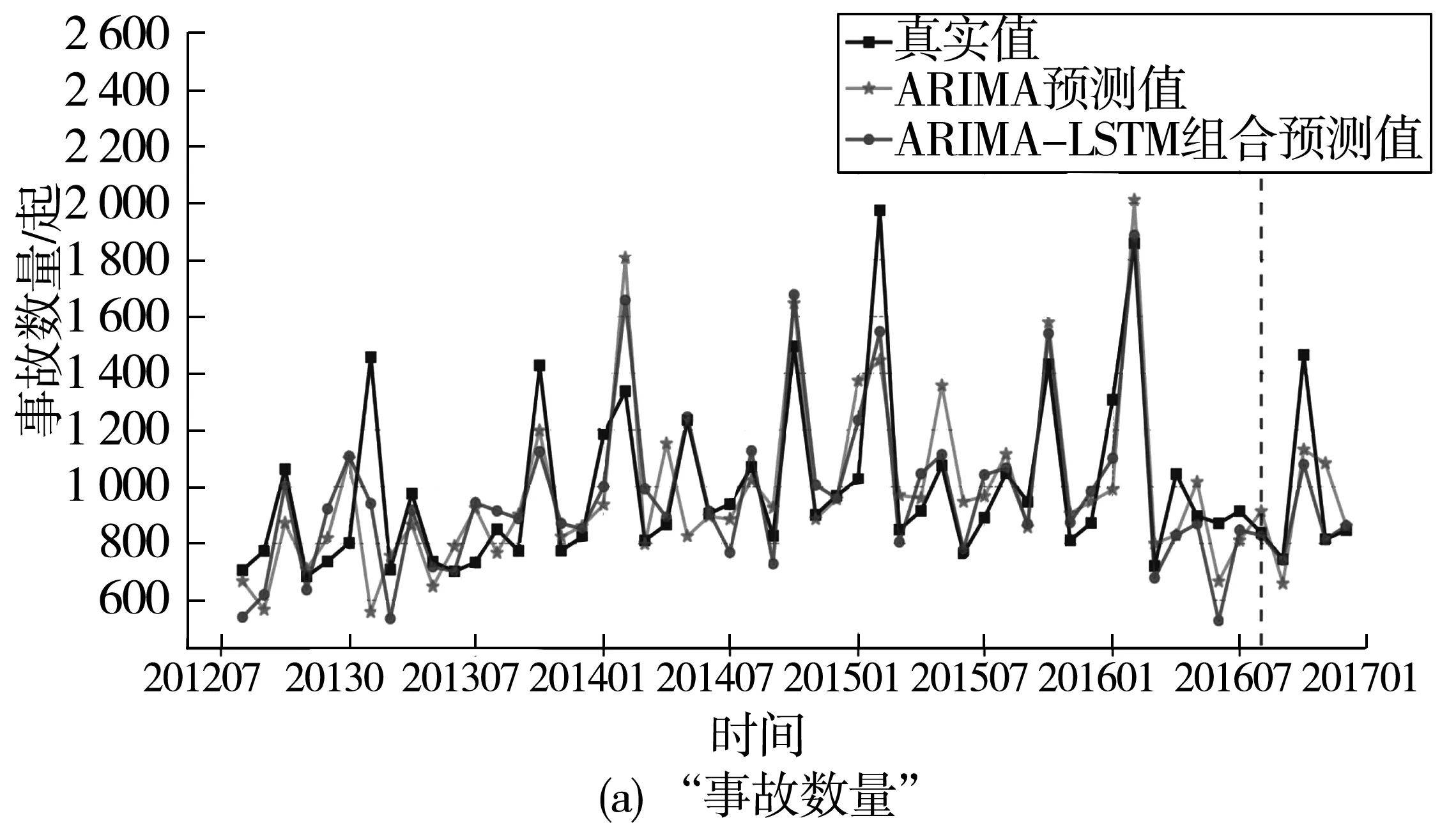
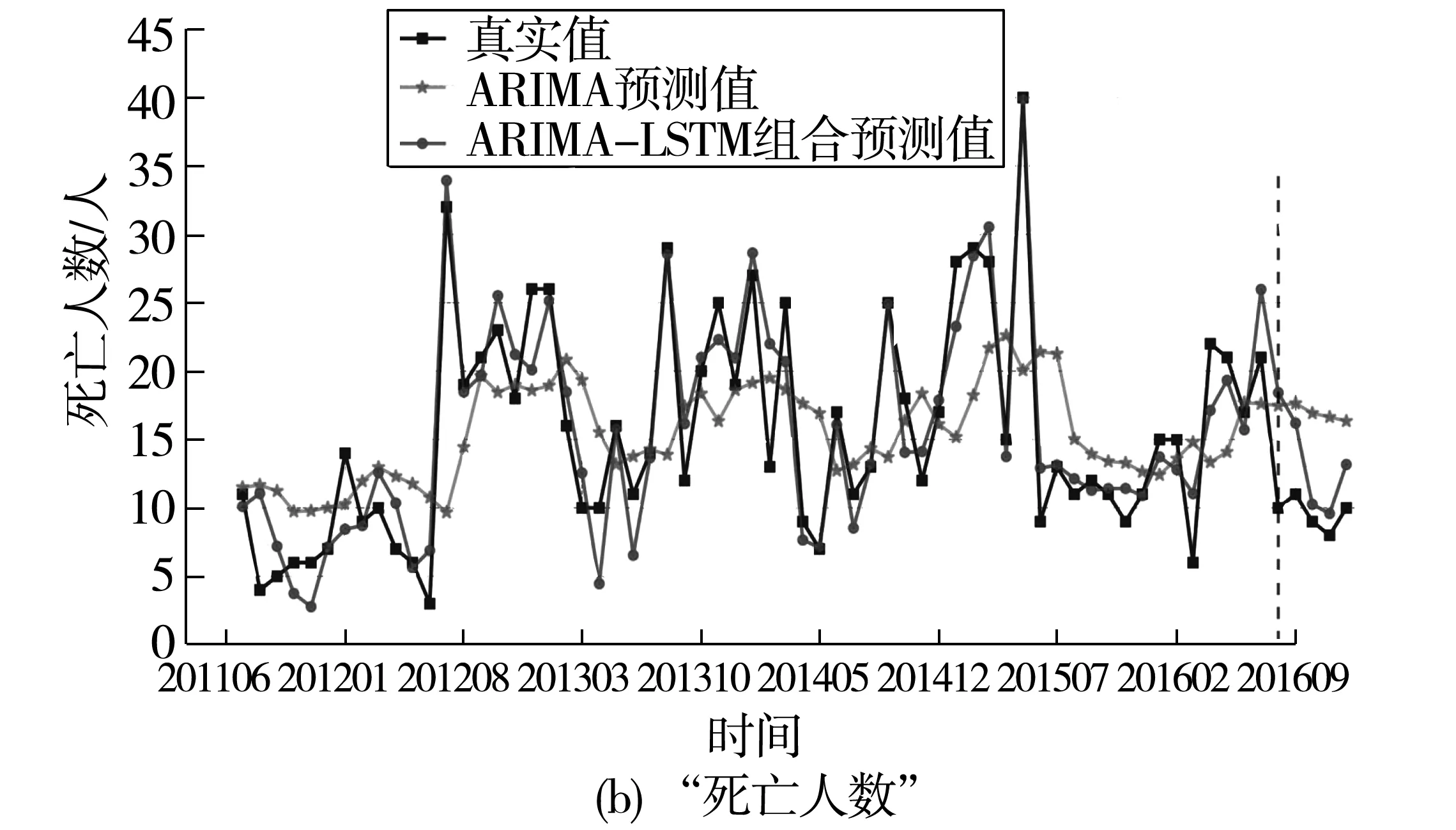
圖9 “事故數量”和“死亡人數”各模型預測結果對比Fig.9 Comparison of the predicted results between models of “Number of accidents” and “death toll”
采用RMSE以及MAPE來衡量模型的預測效果,如表4。可以看出組合預測模型的各項指標更優,以“死亡人數”組合預測模型改善最為顯著,其 ARIMA-LSTM組合模型與ARIMA模型相比,RMSE與MAPE分別降低了4.02與27.99%,即相較于單一模型,組合模型的RMSE和MAPE分別改善了55.83%和54.80%;“事故數量”的ARIMA-LSTM組合預測模型的RMSE和MAPE相較于ARIMA模型分別降低了51.91與3.71%,組合模型的RMSE和MAPE分別改善了23.15%、23.29%。
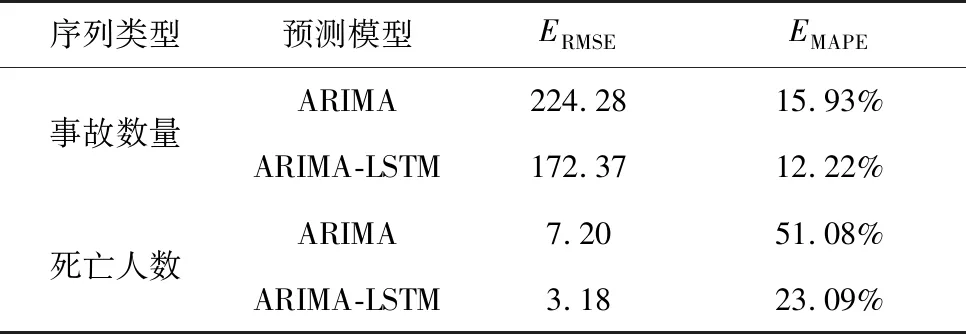
表4 模型評價Table 4 Model evaluation
4 結 論
1)選取事故數量和死亡人數兩項指標,建立了基于ARIMA-LSTM的高速公路交通安全時序組合預測模型,通過ARIMA模型可捕捉各項指標時序數據中的線性因素,而LSTM神經網絡模型可預測各指標殘差序列中的非線性因素。
2)單一的ARIMA模型對“事故數量”序列的預測效果較好,平均絕對百分比誤差為15.93%;ARIMA模型對“死亡人數”原始序列的預測精度一般,但總體上能預測出死亡人數的變化趨勢。
3)ARIMA-LSTM組合預測模型相較于單一的ARIMA模型在預測能力上有一定程度的提升,能夠更好挖掘出時間序列中的有效信息。對于事故數量指標,組合預測模型的RMSE和MAPE相較于ARIMA模型分別改善了23.15%、23.29%;對于死亡人數指標的改善更為顯著,與ARIMA模型相比,其組合模型的RMSE和MAPE分別改善了55.83%和54.80%。

