基于Shapley值分配原則的鐵路應急資源調度研究
湯兆平,鄒 揚,劉鈺玲,孫劍萍
(1. 華東交通大學 交通運輸工程學院,江西 南昌 330013;2. 寧波市軌道交通集團有限公司,浙江 寧波 315101)
0 引 言
隨著我國鐵路路網密度的持續增大,列車運行時速不斷提高,行車組織愈加復雜,路網之中出現多個地點同時發生事故的可能性也逐漸增大,如遇到特殊地形地質或自然災害時,更容易引發大規模的鐵路突發事故。由于事故發生存在不確定性,以及鐵路應急資源的儲備成本高等特點,各救援點的應急資源不可能無限制配備[1]。因此,針對救援初期資源不足的情況,對多事故點多救援點的資源公平調配問題的研究顯得尤為重要。
在多事故點-多資源-多救援點的應急資源分配調度方面,相關學者已進行了一定的研究。如王東海等[2]通過TOPSIS模型來評估事故點的救援優先權,模型中以成本系數和時間系數的形式表示事故點的優先權,使救援優先權較高的事故點優先獲得其所需的資源。范雪琳[3]以應急控制程度最大化和線路停運損失最小化為目標,研究了鐵路接觸網多故障的資源調度問題;王旭坪等[4]以效用滿意度和需求滿意度為目標來描述并求解救援初期的應急物資分配問題;CHAI Gan等[5]提出了一種以救援路線行程時間估計為依據的應急救援資源調度方法,根據應急救援路徑的總長度與救援車輛排隊在時間上的延誤的對應關系,計算出救援路徑行程的大致時間,并以此為據建立改進的資源調度模型;湯兆平等[6]考慮事故點的需求為模糊需求,運用塔木德公平分配理論對大規模鐵路突發事件下多事故點-多救援點-多種資源的資源分配問題,基于此分配原則進行資源調度,可以較好地保持博弈規則的公正性;陳治亞等[7]通過AHP模糊綜合評價法對鐵路多事故點的受災程度進行評分,并以運輸成本和懲罰成本最小化為目標建立資源調度優化模型。Shapley值分配原則能夠兼顧公平與效益,已有學者對其在收益分配機制方面進行了研究。張宇翔等[8]通過考慮項目內部成員的產權比例、風險承擔和工作貢獻,構建了國際高鐵項目收益分配概念模型,并采用合作博弈理論和Shapley值法對收益分配方案進行了修正;WANG Yuanhua等[9]研究了在n人合作對策下的對稱和加權Shapley值,利用博弈者定義的非對稱權重設計加權Shapley值的收益函數,從而保證最優分配是純Nash均衡;趙璇[10]針對產學研聯盟收益分配中存在收益值的不確定性以及聯盟的不穩定性2個問題,使用估計值來衡量聯盟的收益,建立了基于H-Shapley值法的產學研聯盟收益分配模型,得出的H-Shapley分配解能夠使產學研聯盟合作保持長久穩定;楊靛青等[11]利用Choquet積分定義模糊合作對策中局中人可能形成的多層級聯盟結構,在此基礎上提出Shapley值解概念及其解法,通過算例分析合作對策Shapley值和Banzhaf值的異同特性,結果表明Shapley值的聯盟結構相對固定;武士超等[12]通過熵值法和Shapley值法對快遞行業組建末端配送聯盟利益進行分配,最后對影響因素權重進行修正,得到最終分配結果,結果符合個體理性和集體理性;K.M.CUBUKCU[13]證明了在合作博弈框架下發展起來的Shapley值公平分割方案,可以實現土地所有者之間剩余開發權的公平分割。
筆者將Shapley值分配原則引入鐵路應急資源的分配中,通過計算出各事故點對不同資源的Shapley值以確定分配比例和分配量,再綜合考慮調度時間和調度成本等因素建立優化模型,最后進行模型求解。使調度方案實現公平與效益的統一,在減小系統綜合損失的同時,該種分配方案也更易被多方接受。
1 Shapley值分配理論
假設合作博弈系統內有n個成員,由N={1,2,…,n}表示,不同成員之間互相排列組合成不同的聯盟S(S?N),特征函數w(S)為聯盟S的收益,w(S)具有超可加性,其性質表示為:若聯盟S1和S2之間沒有交集,則S1和S2合并形成新聯盟的收益應該不小于聯盟S1與S2的收益之和[14]。即:
(1)
聯盟內成員i的收益為該成員i在所有聯盟的參與中創造的邊際貢獻均值,表示為φi(w):
(2)
式中:S為包含成員i的所有子聯盟;|S|為子聯盟S中成員的個數;w(S{i})為子聯盟S除去成員i后的收益;w(S)-w(S{i})為成員i對子聯盟S的邊際貢獻;θ(|S|)為聯盟S出現的概率,其計算公式為:
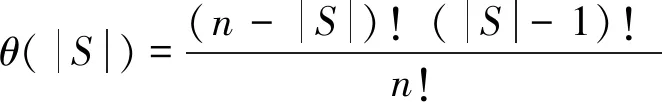
(3)
2 問題描述
3 多目標優化模型建立
為了方便計算,筆者只考慮由于事故造成的直接損失。由于鐵路應急救援具有緊迫性,因此優化模型目標函數的主要考慮因素是資源調度的時間最短,其次還應該盡可能使資源的調配成本最小。
根據上述分析,建立多目標優化模型如下:
(4)
(5)
(6)
(7)
(8)
(9)
(10)
模型中:式(4)為救援時間最短的目標函數;式(5)為總調度成本最小的目標函數;式(6)為事故點i和救援點j之間構成事故點-救援點對;式(7)為事故點i和救援點j之間不構成事故點-救援點對;式(8)為應急救援點向事故點實際運送應急資源的量等于救援點對該事故點應急資源的調運量總和;式(9)為應急救援點向事故點實際運送應急資源的量應該小于或等于救援點j的資源儲備量;式(10)為救援點向事故點的實際運送量應該不小于0。
4 基于Shapley值分配原則的需求點資源分配數量的確定
將事故點的應急救援工作類比于合作博弈問題,其中的事故點可看作博弈問題中的參與方,應急資源的分配可看作參與項目的過程,各事故點由于應急資源得到滿足所減少的損失可類比于參與到項目中獲得的收益。
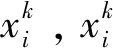
1)列舉出所有包含事故點i的救援方案S,分別計算各個救援方案S下所減少的損失為:
(11)
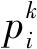
2)計算在救援方案S中除去事故點i后所減少的損失為:
(12)
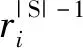
3)計算得到事故點i在救援方案S下的邊際收益為:
(13)
4)根據式(2)得出事故點i對資源k的Shapley值為:
(14)
5)重復上述步驟,分別計算得出各個事故點i(i=1,2,…,n)的Shapley值,從而得到在現有的資源k總儲備量條件下各個事故點的資源分配比例為:
(15)
6)設y為規模比例系數,各個事故點對k資源需求量、分配比例與規模比例系數乘積之和應該與k資源的總儲備量相等,即:
(16)
7)根據式(16),可以得到y的具體數值,進而可以確定各個事故點i對k資源的具體分配數量為:
(17)
5 實例分析
5.1 實例概況
以中國鐵路某局集團公司為例,其局內設共有14個應急救援基地(A1,A2,…,A14),為了便于計算,假設在某局的部分區域內突發鐵路大規模事故,涉及的事故點有3處,分別用N1,N2,N3表示,參與救援的救援基地有5處,分別用M1,M2,…,M5表示。假設該事故中事故點需要的應急資源有醫療救援設備k1和鐵路搶修設備k2兩種。考慮到鐵路貨運單位千米運費以及救援時間成本,將單位救援物資和單位千米的運費設為c=7元,通過參考相關實例并根據決策者的偏好合理假設,將調運時間、調運成本的權重分別確定為ξ1=0.3,ξ2=0.7。各個救援點與事故點之間的信息如表1。
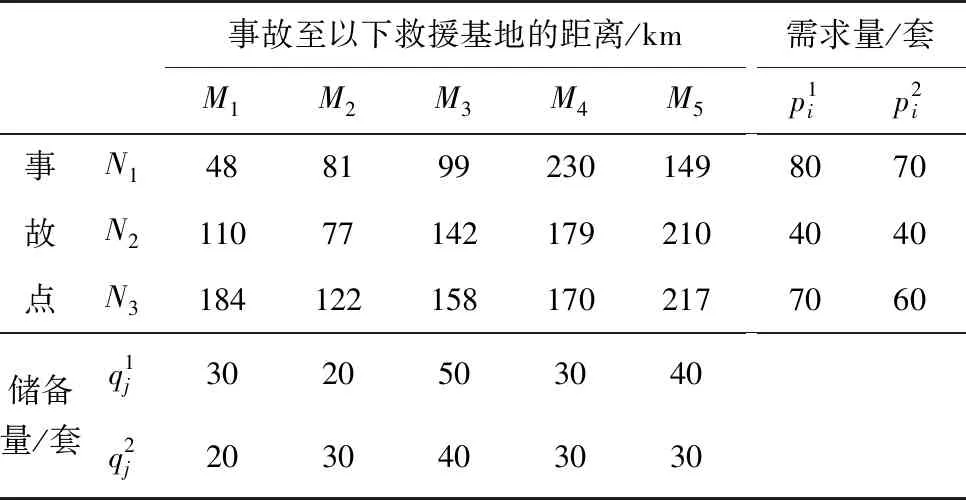
表1 各救援點和事故點信息
5.2 確定各需求點的實際分配數量
5.2.1 資源k1
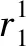
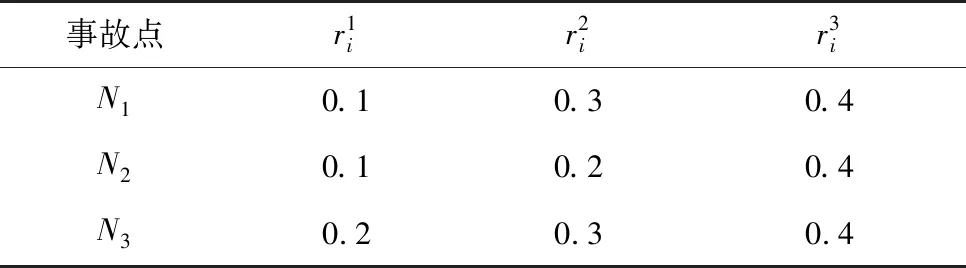
表2 各事故點由于資源k1未能得到滿足引起的損失
計算各個事故點對資源k1的Shapley值。
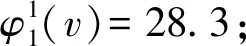
設y1為資源 的規模比例系數,已知資源k1的總儲備量為170,根據公式(16),有:(80×37%+40×24%+70×39%)×y1=170,從而得到y1=2.56。
最后根據式(17)計算得到資源k1的實際分配情況如表3。
5.2.2 資源k2
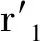

表4 各事故點由于資源k2未能得到滿足引起的損失
計算各個事故點對資源k2的Shapley值。
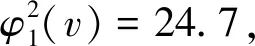
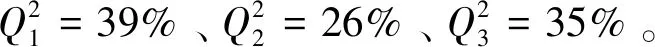
設y2為資源k2的規模比例系數,已知資源k2的總儲備量為150,根據公式(16),有:(70×39%+40×26%+60×35%)×y2=150,從而得到y2=2.55。
最后根據式(17)計算得到資源k2的分配情況如表5。

表5 資源k2分配情況
5.3 調度方案的最優解
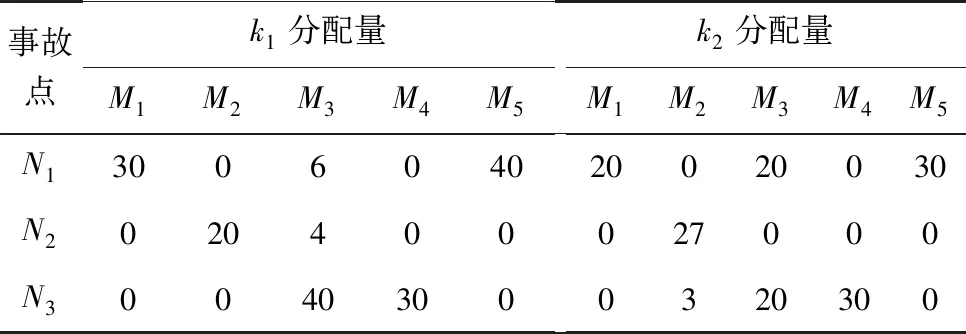
表6 最優調度方案
將優化后的結果代入式(4)和式(5),并根據調運時間以及調運成本的權重ξ1=0.3,ξ2=0.7,計算得到本次救援的最小綜合成本為194 221.3元。
6 多種分配方法下的比較分析
在資源公平分配方面,主要有約翰·羅爾斯的公平分配理論、亞里士多德的分配正義理論、Shapley值分配理論以及塔木德公平分配理論。
為了體現Shapley值分配原則在鐵路應急資源調度方面的良好適用性,下面以資源k1為例,對比分析比例分配理論和塔木德分配理論對上述案例的資源分配情況,計算得到具體分配情況見表7(不限定整數)。
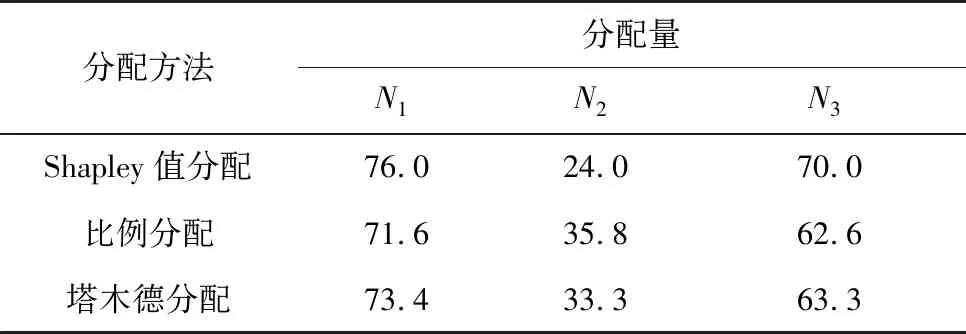
表7 不同分配方法下各事故點對資源k1的分配量
從資源需求量上看,事故點N1對資源k1的需求量最大,可以認為該事故點受災相對嚴重;N2的需求量最小,受災相對較輕。從3種方式的分配結果可以看出,Shapley值分配法分配給受災最嚴重的事故點N1的資源數量最多,其次是塔木德分配法,比例分配最少。該分配結果證明Shapley值分配法對受災最為嚴重的事故點進行了重點考慮N1,充分反映了在救援初期資源不足的情況下,Shapley值分配方法的天平是傾向于弱者的。對于受災程度相對較輕的事故點N2,資源分配數量最多的是比例分配法,其次是塔木德分配法,Shapley值分配法最少。3種分配方法分派給各個事故點的資源數量雖互有差異,但它們的變化范圍處在同一數量級上,說明Shapley值分配法在優待弱者的同時,依然保證了博弈的公平性原則。
3種分配方法對資源k1的最優調度方案如表8。

表8 不同分配方法下資源k1的最優調度方案
將表8得出的最優調度方案代入式(4)和式(5),得到比例分配和塔木德分配對于資源k1的綜合成本分別為105 804.7元和105 480.3元,而Shapley值分配法的綜合成本為105 457.8元。由此可知,根據Shapley值分配原則進行資源分配調度時所產生的綜合成本最小,能最大程度上減少事故造成的經濟損失。
與比例分配原則相比,Shapley值分配原則基于公平分配理論,根據減少損失的程度對事故點所需資源進行分配,考慮每種分配方法所減少的邊際損失,體現了“按勞分配”的原則,具有較強的合理性。相比于塔木德分配原則適用于應急資源較為充足的情況,Shapley值法分配原則在大規模鐵路突發事件初期,應急資源儲備量不足以滿足所有事故點的需求量的情況下更為適用。
7 結 論
針對鐵路突發事故初期多事故點多救援點的資源分配問題,通過綜合分析現有的資源公平分配方式,采用Shapley值分配法對各需求點進行了資源分配,在此基礎上以救援時間最短、資源運輸成本最小為目標建立多目標優化模型,并借助Lingo軟件求解,得到的結論如下:
1)將Shapley值分配原則用于鐵路應急資源調度工作中,為大規模鐵路突發事件下多事故點-多救援點-多種應急資源的資源調配提供了新的思路和方法。通過Shapley值計算結果來衡量各個事故點應急資源得到滿足時所減少損失的程度,并以此計算各事故點進行資源分配的比例系數,這個過程既考慮了分配的效益,又兼顧分配的公平性原則。
2)將Shapley值分配方法對資源k1的分配結果與比例分配和塔木德分配方法的分配結果進行對比,結果表明Shapley值分配方法能更好地考慮受災程度相對嚴重事故點。并且3種分配方法分派給各個事故點的資源數量雖互有差異,但它們的變化范圍處在同一數量級上,說明Shapley值分配法在優待弱者的同時,依然保證了博弈的公平性原則。

