基于PSO-SVDD的齒輪箱故障診斷*

駱東松 薛 鑫

（蘭州理工大學電氣工程與信息工程學院 蘭州 730050）

1 引言

運行可靠始終是旋轉設備的第一安全底線，也是企業發展的根本保障。齒輪箱作為旋轉設備中較復雜的結構部件，工作運行環境復雜，故障種類繁多，在服役期內，受徑向和軸向負荷突變，引起嚴重損傷，直接影響設備的安全運行，甚者引發安全事故。因此，設備的在線檢測和故障判斷對齒輪箱的維護和或更換具有重大的變被動為主動的戰略意義。軸承箱作為復雜機械部件，故障數據獲取存在困難，且不同設備之間故障數據存在較大差異，導致常用的故障監測方法因故障數據的缺乏以及系統開發的困難程度，成為制約齒輪箱設備狀態監測的一個重要原因。

支持向量數據描述（SVDD）是對支持向量機（SVM）的一種延伸。與傳統的SVM 算法不同，SVDD 是一種單值分類方法，就是可以對某一類數據進行分類，SVDD 的支持向量決定的最小超球體能夠包含被分類數據中的絕大部分，對樣本依賴度小，不會出現過擬合，具有計算速度快、魯棒性強、適合小樣本數據的處理，更適合在嵌入式設備中的應用，同時在文本分類、垃圾郵件識別、圖像分類、蛋白質分類中被廣泛應用。

本文提出了一種經PSO 優化后的SVDD 算法，該算法在本文用來對齒輪箱故障進行診斷。利用經典的振動信號處理方法，對不同故障狀態下齒輪箱振動數據進行降噪與特征參數的提取，用SVDD算法將處理后的振動數據先求取支持向量，然后利用支持向量求取最小超球體，進而求取特征參數所存在的特征域，構造能夠表征羅茨風機齒輪箱在不同故障下運行狀態的特征域，對相關結果進一步分析總結出本文提出的方法是可行的［1］。

2 支持向量數據描述（SVDD）

SVDD 早期首先是由TAX 等人結合了SVM 思想提出來的，是低維空間向高維空間的延伸。在機械故障診斷、圖像檢測等方面得到了廣泛應用，因為有了核函數的引入，導致SVDD 的性能將會直接受到核參數選擇的影響，要想達到理想的效果只有選擇較為合適的核參數才能實現［14］。SVDD是一種單值分類算法，可以對單組數據進行空間向量描述。

最小超球體示意見圖1，其中：a 是最小超球體的球心，R 是最小超球體的半徑。假設樣本集空間中包含N 個樣本xi（i=1，2，…，N），在實際工程當中，由于外界噪音的干擾，在構造超求體時，會將一些奇異值包含在內，使得分類準確率下降或構造的超球體并非為最小超球體。為減少奇異值的影響，引入松弛變量ξi［2］，對應優化問題的數學描述為

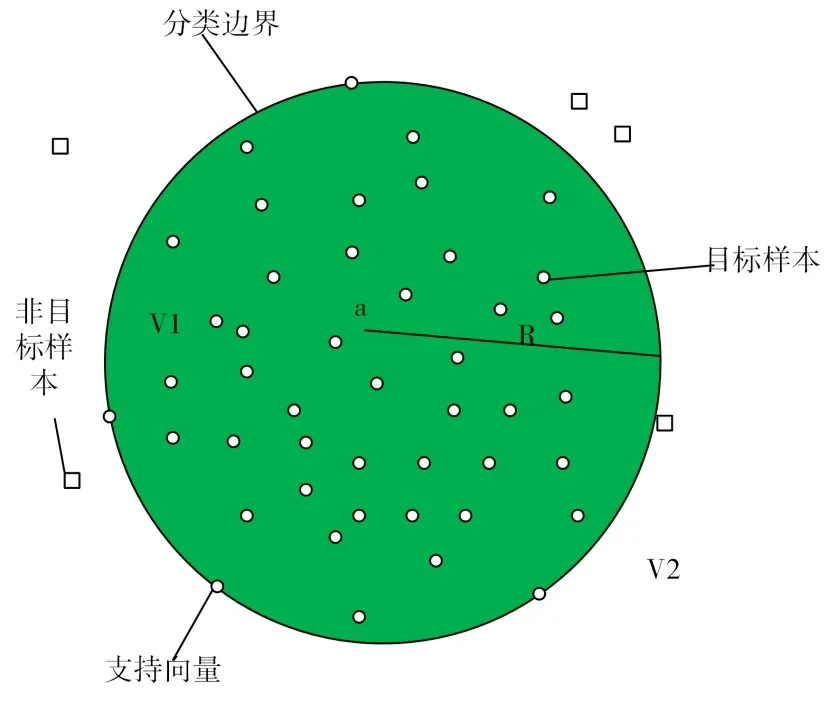
圖1 二維空間超球體示意

式（1）中：C 為懲罰因子，用來平衡目標樣本和非目標樣本的比例。

為方便求解，引入拉格朗日乘子。

式（2）中：αi≥0，βi≥0 為引入的拉格朗日乘子。將LP(a，R，α，β)由L代替，則式（2）的對偶形式為

對該優化問題進行求解可以得出αi的值，當αi≠0 時，其對應的樣本即為支持向量［2］，超球體的球心與半徑的求解公式為

對于任何一個測試樣本點z，如果滿足：

通常情況下，在低維空間中數據的分布不會呈球狀，故引入徑向基核函數K(xi·xi)代替式（3）中的內積運算，將低維空間中的非線性問題轉化為高維空間中的線性問題［15］，求解過程變得簡單。即

測試樣本z為目標樣本只需滿足：

3 線性變換粒子群優化算法

粒子群優化算法（Particle Swarm optimization，PSO）又翻譯為粒子群算法。PSO 初始化為一群隨機粒子（隨機解），然后通過迭代找到最優解。假設n 維空間中第i 個粒子的位置和速度分別為Si=(Si1，Si2，…Sid) 和Vi=(Vi1，Vi2，…Vid) ，為了找到全局最優解，算法進行迭代計算，每次迭代計算中，粒子通過跟蹤個體最優解Pbest，Pi=(Pi1，Pi2，…Pid)與全局最優解（gbest）來更新自己［14］。

粒子通過式（8）更新自己的速度和位置：

其中：ω為慣性權重因子，c1和c2為大于0 的學習因子，r1和r2為隨機數，其分布區間為0～1。

在PSO 算法中ω是最重要的可調參數，t和t+1 分別代表迭代次數當前值和下次值。由于慣性權重越大越有利于PSO算法跳出局部極小點［14］，防止算法進入局部循環，提高算法算法收斂速率，采用可變化的權重因子，權重因子ω在定區間內進行變化，以適應不同時期權重因子的最優值。ω隨算法迭代次數的變化公式為

其中：ωmax-ωmin表示權重因子的取值空間，t代表當前迭代次數，tmax代表最大迭代次數。

優化PSO 算法的參數組[K，α]，將其初始種群數量初始化為10，最大迭代次數初始化為30，學習因子c1和c2都初始化為1.5，根據圖2 可以看出PSO 在尋求最優解的過程中，局部極小值EP隨種群進化，當迭代次數為4時，算法收斂。

圖2 PSO種群進化

4 基于PSO-SVDD的故障診斷過程

針對某熱源廠大型羅茨風機減速齒輪箱故障診斷中存在的響應時間長，響應精度低等問題。本文提出將粒子群算法PSO 與支持向量數據描述SVDD 相結合，通過兩種算法的結合，發揮各算法的優勢，而后對齒輪箱進行故障診斷。故障診斷過程如圖3所示。

圖3 故障診斷過程

步驟1：對廠區羅茨風機運行振動數據進行采集并進行特征提取，樣本數據集包括：正常樣本數據集D1、點蝕樣本數據集D2、點蝕磨損樣本數據集D3、斷齒樣本數據集D4、磨損樣本數據集D5、斷齒磨損樣本數據集D6。

步驟2：利用優化后的PSO-SVDD 算法對樣本數據所包含的正常樣本和已知故障類型樣本數據構建超球面，用做后面兩步故障類型判斷的依據。

步驟3：利用數據集D1構建的故障診斷模型對測試樣本進行第一輪診斷，判別式為函數式（7）。如果滿足則說明羅茨風機運行正常；反之，則說明樣羅茨風機存在故障。

步驟4：第一輪診斷后部分測試數據顯示該齒輪箱存在故障，對存在故障信號的測試數據進行第二輪診斷。分別將測試數據用數據集D2構建的故障診斷模型進行故障診斷，判別式依然為函數式（7），若輸出有故障，則實際數據并無該故障。同理，依次用不同故障樣本數據構建的超球面對測試數據進行故障診斷，當輸出顯示無故障，則測試數據存在此類故障，并進行故障顯示。

5 試驗分析

本次設計應用于某熱源廠2#羅茨風機的變速齒輪箱中，模型訓練數據集通過設計的下位數據采集器采集得來，設備額定功率為75KW，額定轉速為800r/min，驅動端軸承型號為SKF6205 數據集采集轉速為額定轉速的70%，即羅茨風機的變頻器頻率為35Hz，振動信號采樣頻率為12KHz，16 位AD采樣，采樣時長8s，將采集到的數據集劃分為60組，其中40 組作為訓練數據，取SVDD 算法的拒絕率為百分之一，徑向基核函數的σ參數為5，進而求出支持向量、球心和半徑。其余20 組作為測試數據。齒輪箱狀態包括正常、點蝕、點蝕磨損、斷齒、磨損以及斷齒磨損。經PSO-SVDD診斷后得到的故障診斷結果如圖4所示。

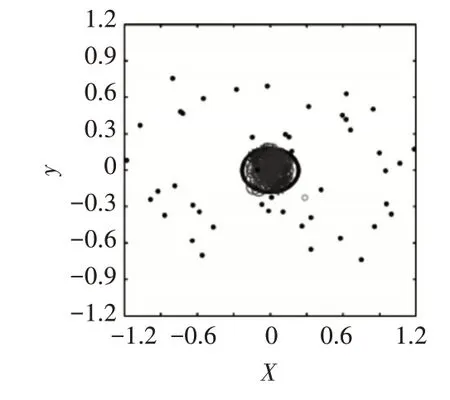
圖4 PSO-SVDD算法診斷結果

傳統的SVDD 算法，作為典型的單值分類器，其缺點也是顯而易見，通過該模型只能簡單判斷出設備在運行過程中是否出現故障，但對于出現故障的具體類型卻不能夠做出判斷，即使如此簡單也已經對事故的預防起到了重大的作用。本文提出的通過將單一故障樣本假設為正常樣本進行的第二次故障診斷，通過邏輯運算，可以很好地解決SVDD 算法因其單值分類這一特性所造成的無法對機器的故障類型做出更準確的判斷這一缺憾，完成了齒輪箱相應的故障診斷，此法亦可用于其他部件故障診斷中。

6 結語

齒輪箱的故障診斷在大型風機系統中是不可或缺的一環，但僅憑單一的傳感器及傳統的齒輪箱故障診斷方法很難準確診斷出具體故障類型，影響設備安全運行以及企業的經濟效益。

本文提出的利用PSO-SVDD 單值分類器對采集到的振動數據進行兩輪診斷，通過對結果的邏輯運算，分析出齒輪箱故障。在用SVDD 模型進行故障診斷時，核函數的選擇是重中之重。本文選取的徑向基核函數相比于其他核函來說較為簡單，編程難度較低。試驗結果表明，與傳統的旋轉設備故障診斷技術相比，該診斷算法更加簡單，對硬件要求更加簡單，適合便攜式故障監測設備開發所需要的智能診斷算法。

本課題由于傳感器安裝位置、傳感器誤差和特征提取誤差導致的數據間的沖突忽略不計。