基于改進NURBS曲線的水下機械臂軌跡規劃*

孫颙琰 郭文勇 孫云嶺 王晶航

（海軍工程大學動力工程學院 武漢 430033）

1 引言

水下機械臂已經越來越多的應用于艦船水下檢測與維修［1］，為了水下機械臂能夠穩定、快速地完成水下維修任務，滿足艦船水下應急維修的需求，基于實驗室的六自由度水下機械臂如圖1所示，對水下機械臂進行軌跡規劃研究。

圖1 水下機械臂實物圖

機械臂通常主要是在關節空間或笛卡爾空間進行軌跡規劃［2］。在關節空間中進行軌跡規劃主要是針對機械臂各個關節變量，將關節的位移、速度、加速度等參數表示成時間的函數，由于不需要考慮末端執行機構的運動狀態，該方法主要應用在點位控制（PTP）中。在笛卡爾空間中的進行軌跡規劃則主要針對末端執行機構得運動狀態，將末端執行機構的位姿、速度、加速度等參數表示成時間的函數，該方法適用于連續軌跡控制（CP）中，常運用于對末端執行機構的運動狀態有特殊要求的軌跡規劃［3］。

笛卡爾空間軌跡規劃對于機械臂末端雖然能準確控制位姿、速度等參數，但是在規劃過程中需要不斷地進行運動學逆解來得到其他關節角，將位姿序列映射成關節角度，而運動學逆解的運算量比正解的運算量大了好幾倍，使得求解時間增加，而在關節空間中進行軌跡規劃則省去了這一步，使得計算量大量減少，不用考慮奇異問題［4］，還可以直接反映出各關節的參數變換，機械臂各關節的速度、加速度和加加速度等參數在關節空間中實時性更好，且控制和描述更方便［5］，因此本文采用在關節空間下進行軌跡規劃的方法。

2 關節空間軌跡規劃方法

在關節空間中進行軌跡規劃最常用的方法有三次多項式曲線插值、五次次多項式曲線插值、B樣條曲線插值和NURBS曲線插值等。

2.1 NURBS曲線插值算法

B 樣條曲線是貝塞爾曲線的一般化，就是通過控制點進行局部控制形狀的曲線，廣泛應用于曲線擬合中。B 樣條曲線在保留了貝塞爾曲線優點的基礎之上，同時也克服了它的缺點，能夠對曲線進行更加方便的控制，在曲線次數較低時仍有較多控制點去控制曲線；可以通過某個控制點去修改局部曲線而不會導致整個曲線形狀的發生變化；同時有著更好的凸包性質，對曲線的形狀能夠進行更加細致的控制。常用于需要經過多個關鍵節點的軌跡規劃中。司艷偉等［6］對通過分析三次B 樣條曲線和七次B 樣條曲線，證明了三次B 樣條曲線比七次B 樣條曲線運算效率高，且能夠有效的避免龍格現象。Guan Y.S［7］結合三次B 樣條四次B 樣條曲線的優點，提出了4-3-4 復合軌跡規劃方法，該方法在保持較高運算效率的同時，也能夠保證加速度曲線的連續性與平滑性，但無法保證加加速度的連續。

NURBS（Non-Uniform Rational B-Spli-nes）即非均勻有理B 樣條曲線，最早由美國西拉丘茲大學的Versprille 在其博士論文中提出。波音公司的羅溫首先將有理參數曲線曲面引入到了形狀設計中，隨后，1991年在國際標準化組織頒布的工業產品數據交換標準STEP 中，決定將NURBS 確定為定義工業產品幾何形狀的唯一數學方法［8］。為解決插值點較遠時曲線產生尖點和突變問題，Kubota 等［9］采用三次NURBS 曲線插值進行軌跡規劃，發現三次NURBS 曲線能夠較好地控制端點，有效地避免了曲線突變，得到的位移、速度曲線平滑無突變。

無論是多項式插值擬合方法還是B 樣條方法，都具有很大的局限性［10］，比如對小范圍復雜曲線的擬合能力差，范圍過大又需要進行分段處理等。將NURBS 曲線應用在機械臂的軌跡規劃方法中可以解決大部分問題，NURBS 曲線優秀的局部性能由其定義決定，通過改變任意單個參數對曲線形狀的修改，均只影響相應的局部位置，整體性能不變，并且k次NURBS曲線的k-1階導數連續［11］。為降低軌跡規劃所得曲線關節位置的跟蹤誤差，從而減少機械臂的系統損耗，最終達到延長其使用壽命的目的，所提出的軌跡規劃方法須保證結果的位移、速度、加速度平滑并且加加速度連續。故本文采用四階導數連續的五次NURBS 曲線進行插值軌跡規劃。

B樣條曲線方程可以表示為

其中di(i=0，1···，n)是控制頂點。Ni，k(u)(i=0，1···n)稱為基函數，u為節點矢量，是由非遞減的參數組成的序列：u0≤u1≤···un+k+1。

在本文的軌跡規劃問題中，用機械臂運行的時間來表示節點矢量。

B 樣條有著許多種等價定義，其中最為常用的是得布爾-考克斯遞推公式：

由式（2），要確定第i個k次B樣條基函數需要k+2 個節點，節點矢量如下：

ui，ui+1，···，ui+k+1

由于求解曲線方程中相應n+1 個控制頂點需要n+1 個k次B 樣條基函數，而確定這些基函數所需的節點構成整條曲線的節點矢量U，參數的數量為n+k+2。并且在參數u軸上任意一點u∈[ui，ui+1]處，至多有k+1 個k次B 樣條基函數是非零的，即：

Nx，k(u)(x=i-k，i-k+1，···i)≠0

因為適用于自由型曲線的B 樣條曲線無法滿足初等曲線的要求，于是把B 樣條方法改造成為有理B 樣條方法來滿足使用要求。而在實際應用中，B 樣條曲線往往出現非均勻的特性，所以研究者們決定將這種曲線稱為非均勻有理B 樣條曲線，即NURBS 曲線。之所以在軌跡規劃中使用NURBS曲線，是因為NURBS 曲線在進行有理的過程中引入了權因子ω，這就讓曲線有了較好的幾何解釋，并且ω能夠影響曲線的局部變化，這一點在軌跡規劃中有著重要意義［12］。一條k次NURBS 曲線可表示如下：

由NURBS 曲線的定義可知，確定一條NURBS曲線需要知道節點矢量U 和控制頂點di(i=0，1···，n)，由于本文中的節點矢量代表時間分配，是待優化項，可以先采用平均分配或隨機分配的方式給定初始值，確定NURBS 曲線后再對時間進行優化。所以，再通過已給定曲線需要經過的路徑點求出出NURBS 曲線的控制頂點，就能夠畫出NURBS曲線。

給定m+1 個需要經過路徑點qi，其中i=1，2，···，m-1。為方便計算取ωi=1。

則k次B樣條曲線方程就可以簡寫為

由于控制頂點d0和dn分別與路徑起點q0與終點qm重合，故d0和dn兩個控制點已知，還需求出n-1 個未知控制頂點。將節點值帶入式（4），即：

由式（5）可得n-k=m+1 個方程，分別對應m+1 個路徑點。另外，軌跡始末速度和加速度的方程如下：

其中、為關節初始速度與加速度，、為其關節停止時速度與加速度，一般均設置為0。

于是現有n-1 個未知參數，n-k+4 個方程，當k=5 時，位置參數與方程式數相等，故當使用5次NURBS 曲線對關節位置進行插值所得軌跡曲線時，可以將初始速度與加速度、停止速度與加速度作為邊界條件。由曲線特性可知，五次NURBS 曲線是C4連續的，可以滿足加速度與加加速度曲線連續的要求。根據給定軌跡點可以求出NURBS 曲線的全部n+1 個控制頂點。再根據式（3）得到五次NURBS曲線方程。

2.2 基于五次多項式速度控制的NURBS 曲線插值算法

通過NURBS 曲線插值算法得到曲線，會產生曲率突變，曲線峰值過高現象，導致機械臂速度突變，抖動嚴重，甚至超過機械臂的加減速度的最大范圍，從而無法完成規定軌跡。為改進一般NURBS 曲線插值算法的缺點，提出一種基于五次多項式速度控制的NURBS 曲線插值算法，簡稱QV-NURBS曲線插值算法。

該改進算法首先通過NURBS 曲線插值得到軌跡曲線，然后通過分析曲率的變化情況找到特征點，將曲線分成曲率平緩段和曲率突變段，通過對曲率突變段的曲線進行分析，獲該突變段的速度、加速度以及加加速度等參數，采用五次多項式對該段進行速度規劃控制，利用式（7）的C4連續性，通過控制速度使得曲率突變段更加平滑，實現在突變段能夠穩定運行，以保持機械臂全程的穩定性。

該算法分為5步：

1）根據式（2）和式（3），由給定的時間節點矢量和軌跡點求出NURBS曲線。

2）掃描特征點。特征點包括曲線間斷點和曲率突變點。曲線間斷點一般位于節點處，能夠通過節點矢量得到，不在節點處的大曲率點可以利用式（7）進行判定得到。

其中，ρi為第i各插值點的曲率半徑。

3）判斷相鄰特征點的速度規劃交叉類型。當兩相鄰特征點之間的曲線弧長出現較小情況時，一般由于加速度限制，速度就無法加速至最大。兩相鄰特征點的速度軌跡規劃就出現了交叉區域。具體分為以下七種類型［13］。

類型1：速度軌跡規劃無交叉區域。其中為第i-1 個特征點加速度階段的位移，為第i個特征點減速階段位移，Si為第和第i個特征點間的曲線弧長。

4）針對上訴7種類型進行速度規劃。

（1）若判定為類型1，則加速至最大速度Vmax后，然后保持勻速運，最后到減速點后減速。

（2）若判定為類型2或類型5，速度加速到Vi后減速。Vi可以使用二分法［14］計算得到。

（3）若判定為類型3或類型4，以起始特征點開始，按照五次多項式軌跡曲線運動至終止特征點，其中五次多項式曲線的起點、終點速度與起始、終止特征點的速度相同。

（4）若判定為類型6或類型7，則把此類特征點從特征點序列中除去。

5）得到經過五次多項式速度控制的NURBS 曲線，即QV-NURBS曲線。

3 軌跡規劃算法仿真分析

通過表1中的D-H 參數，利用Robotic Toolbox建立機械臂仿真模型，如圖2。機械臂執行一段曲線軌跡，起點A 坐標為（0.557，-0.134，-0.289），終點坐標為（-0.458，-0.028，-0.395），通過逆運動學方程求解出各關節對應的關節角度如表2。

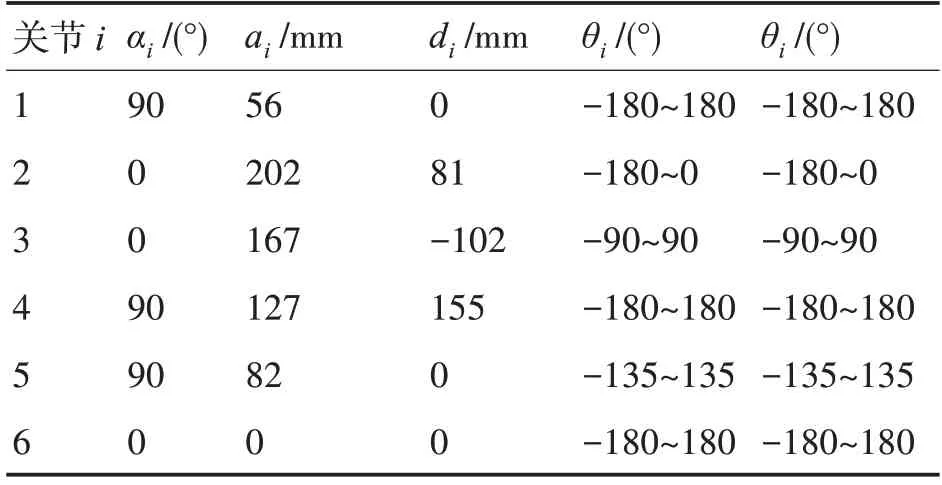
表1 水下機械臂D-H參數

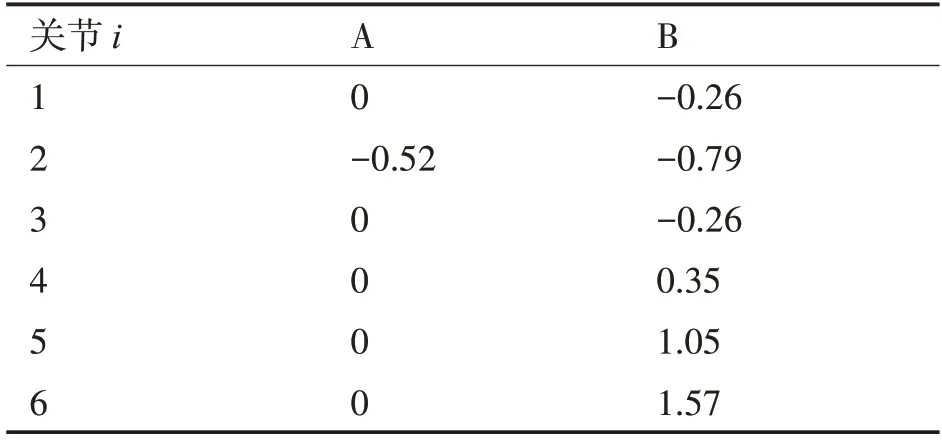
表2 起點與終點的各關節角

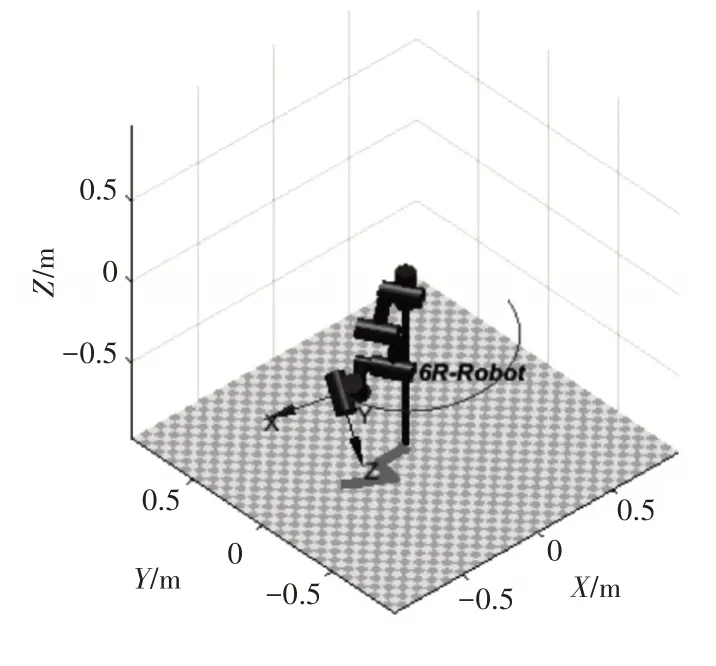
圖2 水下機械臂仿真模型

要求機械臂末端從A 點運動到B 點，運動時間為5s，初始速度和加速度、終止速度和加速度均為0，然后運用五次多項式插值和QV-NURBS 曲線插值進行軌跡規劃。其中通過五次多項式插值得到機械臂各個關節角度位移、速度、加速度以及加加速度曲線如圖3所示。

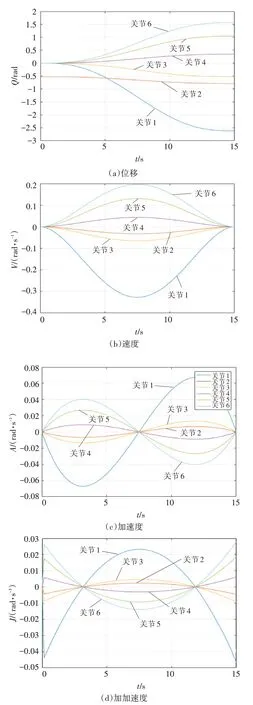
圖3 五次多項式插值各個關節角度位移、速度和加速度曲線

通過圖3可知，五次多項式插值的位移、速度、加速度曲線光滑連續，無突變，但是加加速度曲線初始有突變，但后續也能保持光滑連續且無突變，能夠保證機械臂較為平穩的運行，但在初始階段機械臂所受沖擊較大。

通過QV-NURBS 曲線插值對路徑點進行軌跡規劃，得到機械臂各關節角度位移、速度、加速度和加加速度曲線如圖4所示。

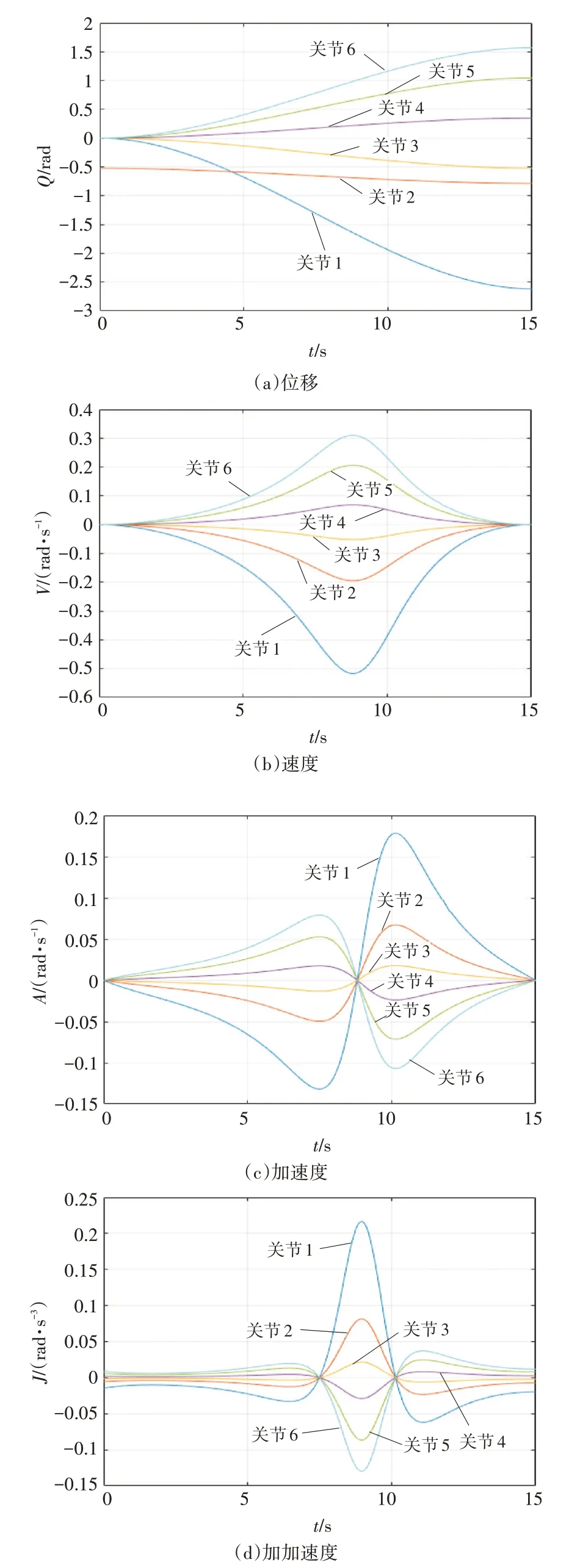
圖4 QV-NURBS曲線插值各個關節角度位移、速度和加速度曲線

通過圖4可知，QV-NURBS 曲線插值算法可以使得機械臂各關節的位移、速度、加速度以及加加速度曲線光滑連續且無突變，使得機械臂能夠在運行軌跡的整個過程中保持運動的平穩性。

通過對兩種種插值算法的仿真對比可知：兩種插值算法均能保持位移、速度曲線的連續平滑；對于加加速度曲線，五次多項式插值在啟動階段有突變，但在運行階段可以較好保持平滑，QV-NUBRS曲線插值則可以很好的保持曲線全程平滑。綜上所述，QV-NUBRS 曲線插值可以解決起始位置的震動和運行過程的不平穩問題，從而完成對各關節運行角度、速度以及加速度的連續有效控制。

4 結語

對關節空間中NURBS 曲線插值算法進行公式推導，并針對NURBS 曲線插值算法的缺點進行改進，提出了QV-NURBS 曲線插值算法，并建立該插值算法在六軸水下機械臂軌跡規劃中的數學模型。

對機械臂軌跡規劃的兩種插值算法進行Matlab 仿真分析，對比優劣性，結果表明基于QV-NURBS 曲線插值的軌跡規劃，使得機械臂末端運行穩定，軌跡平滑連續，任意一條路徑都可以采用QV-NURBS 曲線插值的方法進行規劃實現，為水下機械臂試驗驗證以及機械臂控制系統的設計奠定了基礎。