基于三維走時的沖擊波超壓場重建方法*

劉曉佳 李 劍 孫澤鵬 馬明星 魏曉曼

（中北大學信息探測與處理山西省重點實驗室 太原 030051）

1 引言

爆炸原理是物體在某極短的時間范圍內，釋放射出來大量熱能量，產生高溫，同時破壞性極強，難以通過直接觀察的方式研究。隨著戰斗部研制向著智能化，一體化發展，對于爆炸場的壓力毀傷能力等參量研究具有重要意義。但是由于傳感器節點布設難度大等問題，有限的數據無法直接、全面地判斷彈藥的毀傷能力，因此沖擊波場重建對于彈藥研發過程和定性驗證是至關重要的。

目前，沖擊波超壓場重建的方法有層析成像法，插值重建法等，白苗苗等［1］針對爆炸過程中獲得的數據較少，對反演速度和精度進行分析，加入先驗值進行EM 反演；郭亞麗等［2］針對沖擊波峰值超壓經驗公式的求解的局限性，利用廣義逆方法進行系數矩陣求解，對網格單元加重權，對沖擊波速度場參數進行反演，再進而根據沖擊波峰值的超壓系數與沖擊波速度分布的函數關系可得到超壓分布，其重建的結果遠遠優于經驗公式；楊志等［3］采對沖擊波壓力場進行插值，對比多種方法，表明B樣條插值算法效果最好；趙化彬等［4］提出了一種基于非均勻的有理B 樣條（NURBS）“蛛網”插值的場重建方法；張曉光［5］將多元多項式理論應用到沖擊波峰值插值理論計算中，擬合出波后衰減波形進行彈藥沖擊波重建；姚悅［6］利用Biharmonic 樣條曲面插值算法進行超壓峰值重建；郭晶［7］提出了一種利用攝像機對沖擊波場進行拍照記錄得到沖擊波波陣面的傳播速度對當量進行估算，分析爆炸過程。目前科研人員集中研究二維沖擊波場重建方法。由于爆炸沖擊波是各向異性，常規的二維傳播模型無法有效表征三維空間的傳播特性。因此，三維沖擊波超壓場重建是大威力彈藥毀傷威力評估時亟待解決的瓶頸問題。

針對上述問題，本文在二維走時層析成像模型的基礎上，結合射線追蹤理論，建立了三維沖擊波超壓場重建模型，由于三維超壓場重建問題是大型稀疏矩陣求解問題，且傳統重建算法對邊緣噪聲的抑制效果較差，在層析成像的基礎上結合了壓縮感知理論中的字典學習（Dictionary Learning）聯合全變分（Total Variation）正則化，提出了TV-DL 迭代修正算法，為三維沖擊波超壓場重建及實現其全方位可視化提供了一種新方法，提高了沖擊波超壓場的重建精度。

2 三維沖擊波超壓場重建原理

炸藥在空氣中快速爆炸，瞬時所產生爆炸的爆炸高壓一般可達1010Pa，空氣爆炸的瞬時初始壓力大約為105Pa，爆炸產物極速膨脹，對空氣進行壓縮，形成爆炸沖擊波，由于沖擊波傳播速度較快（瞬時10-6s）可以認為是沿直射線方向傳播的，走時可以通過速度和路徑長度之間的函數來表示，如下式：

其中，t為沖擊波到達探測點的時間，即為走時；L為沖擊波到達測點的傳播路徑；v 為沖擊波波速；S 為慢度；r為對應射線。

假設將重建范圍劃分為M×N×K=J個網格，對式（1）進行離散化處理，如圖1所示。

圖1 三維離散化示意圖

圖2 求解三維投影矩陣流程圖

上圖為三維空間中第i 條射線路徑上射線穿過各網格的投影值之和，其函數表達式如下式：

其中，I 為射線總數，即測點個數；J 為離散網格總數；ti為第i 條射線的走時，即信號到達第i 個探測點前的時間；aij為第i 條投影射線穿過第j 個投影網格的投影射線長度，即系數投影矩陣。

上式可總結為矩陣形式：

其中，A 為投影矩陣向量，其大小為I×(M×N×K)的二維矩陣，S 為慢度向量矩陣，其大小為(M×N×K)×1 的一維矩陣，T 為走時向量矩陣，其大小為I×1的一維矩陣。

在建立三維沖擊波超壓場模型的基礎上，矩陣A 的求解是構建三維模型的關鍵，投影矩陣A 實際上就是I 條射線在三維空間中所有網格的長度信息，本文基于射線追蹤最短路徑的原理計算矩陣A，具體實現流程如下。

在求射線與網格交點的時候，本文采用先得到射線與網格交點一軸的坐標點，根據比例關系求得其他兩軸坐標點，計算步驟如式（4）。

其中，steplen 為步長，lx為區域長度，Bx為傳感器x坐標，By、Bz同理為傳感器的y、z坐標。

本文投影矩陣A 為二維矩陣，索引函數就是將求得的離散網格內的數據還原到對應三維空間位置處。

3 三維重建模型迭代修正算法

三維沖擊波超壓場重建過程中，重建區域大，但是爆炸過程破壞性極大，導致可布設的測點少，三維重建問題是一個典型的病態稀疏矩陣的求解問題。傳統的迭代重建算法重建誤差較大，針對這個問題，利用壓縮感知在稀疏矩陣約束方面的優勢［10～12］，本文在建立三維沖擊波超壓場模型（3）基礎上，利用字典學習對圖像的稀疏表征優勢［14～15］，全變分（Total Variation，TV）最小化將重建問題轉變為求解最小值的問題，TV 最小化理論對圖像邊緣紋理的保真特性［13］，實現對層析模型的正則約束。將TV 最小化與字典學習相結合，重新構建了重建模型：

其中A為投影矩陣，S為重建矩陣，T為投影數據。第一項為重建數據的保真項，第二項為正則項，第三項為字典學習項。μ為保真項系數，λ和β為正則項系數。

求解目標函數（5）步驟如下：

步驟一：固定D和αj，更新重建矩陣S，目標函數為

為求解式（6），引入輔助變量dx，dy，bx，by，得到目標函數（9）：

步驟二：固定S，更新D和αj，對應的目標函數如下：

首先進行字典更新，固定αj更新D，使用K-SVD 方法從重建數據S中學習字典。然后進行稀疏表示，固定D更新αj，采用OMP 方法來更新稀疏表示系數αj。

4 實驗仿真與結果分析

為驗證本文的三維沖擊波超壓場重建模型的可行性，采用ART 算法、SART 算法和TV-DL 方法進行三維仿真重建實驗，比較上述三種算法各自的重建仿真效果以及實現沖擊波三維重建的可視化。

設置大小為24m×24m×12m 的矩形區域為重建區域，區域被均勻地劃分為1m×1m×1m 的網格，重建模型中添加了7.5%的隨機噪聲，炸點位置坐標為（0，0，0），仿真以整個重建區域的四分之一為例，待重建區域大小為12m×12m×12m，被劃分為1728 個網格，布設了36 個傳感器（即36 個測點），圖3為傳感器布設，圖4為各射線與三維網格的交點圖。在圖4中，共有36 條不同顏色的點線，每個顏色的點線代表著一條射線（即爆炸點到一個測點的傳播路徑）與途經網格的交點。

圖3 傳感器分布圖

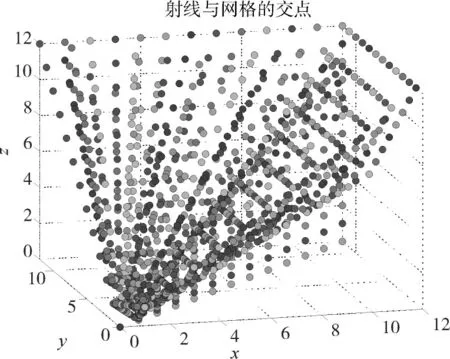
圖4 射線與網格交點

仿真實驗的TNT 當量為5kg，重建模型選用Henrych 沖擊波超壓經驗公式，根據沖擊波峰值超壓與速度的關系將模型轉化為沖擊波波速，將對沖擊波超壓場重建問題轉化為對沖擊波速度場重建問題。迭代終止修正條件若只是滿足給定的迭代次數或終止修正值與初始值的誤差精度，迭代結果會出現局部收斂的情況，本文的迭代終止條件采用修正后的到達時間與初始到達時間的估計誤差小于0.1%，圖5為重建初始模型。

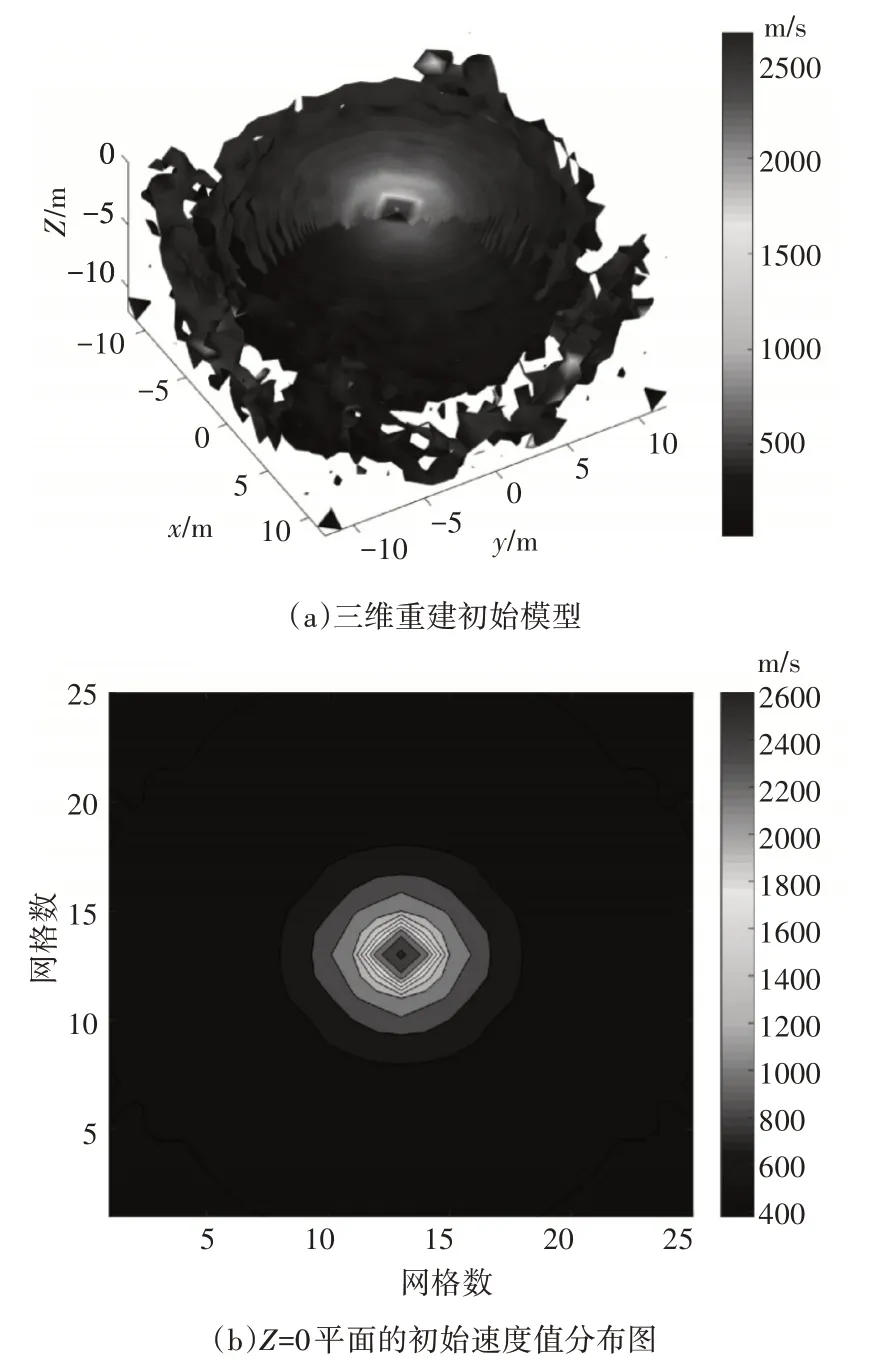
圖5 三維沖擊波重建初始模型

三種方法分別迭代300 次進行反演重建，三維重建結果和Z=0平面的速度值分布如圖6所示。

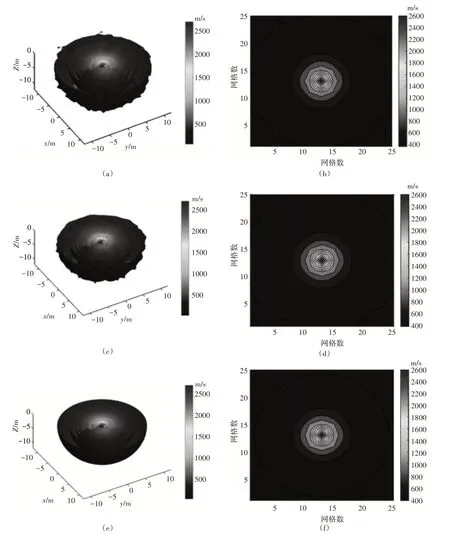
圖6 三種算法分別迭代300次的重建結果

圖6（a）～（b）分別為ART 迭代算法的三維重建結果和Z=0平面的重建速度分布；圖6（c）～（d）分別為SART迭代算法的三維重建結果和Z=0平面的重建速度分布；圖6（e）～（f）分別為TV-DL 迭代修正算法的三維重建結果和Z=0平面的重建速度分布。

由圖6可以看出，與ART 算法和SART 算法的三維重建結果相比，在重建區域邊緣采用本文方法進行的三維重建結果與采用傳統迭代算法的三維重建結果相比更為光滑，為了更直觀地觀察三種方法對于邊緣噪聲的抑制情況，本文觀察了三種重建結果的Z=0 平面的速度值分布，觀察比較圖6（b）、（d）、（f）可以明顯看出，在有效抑制邊緣噪聲問題上，TV正則化具有較大優勢。

為了客觀闡述以上三種算法對于重建區域的重建精度，本文將采用相對誤差（RE）和均方根誤差（RMSE）作為重要評價參數，RE一般用來客觀評價三種方法的重建速度模型與初始速度模型在一個速度重建區域范圍內的各網格之間的實際重建的效果，RMSE 一般用來客觀評價一個整體區域內的實際重建結果與重建初始模型結果的偏離的程度，值越小，表明重建結果越接近實際情況。三種算法重建結果的RE曲線見圖7。

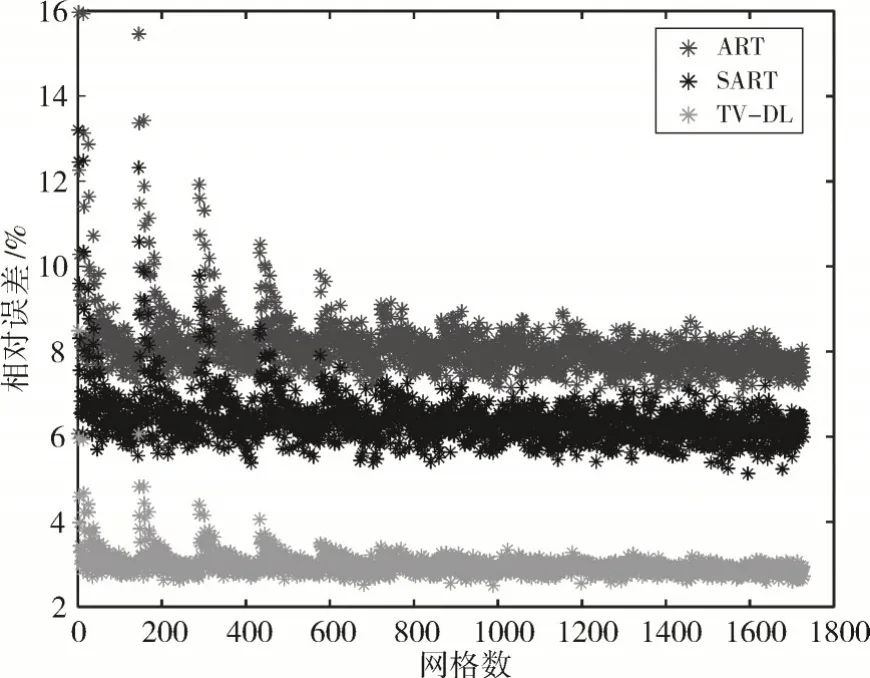
圖7 每個網格內速度的相對誤差

圖7為三種迭代算法重建后的速度與初始速度在重建區域內的1728 個網格中的相對誤差，可以明顯看出，在重建區域內，相對誤差曲線呈周期性衰減，究其原因是重建網格的劃分是逐層排序共記12 層。由圖7可看出曲線衰減大致分為12 段，爆炸沖擊波場在近場區超壓值變化極快，與遠場相比，重建誤差大，因此，誤差曲線呈分段衰減的趨勢。在圖7中，TV-DL算法的相對誤差基本能保持在3%左右，與ART 算法相比，降低了5%左右，與SART算法相比，降低了3%左右。進一步用均方根誤差來作為重建后整體誤差，三種算法的RMSE 值如表1所示。

表1 重建結果的均方根誤差

已知重建區域整體的速度范圍大約在400m/s～3000m/s，由上表可知，三種算法整體的速度場重建的總誤差依次為45.81m/s、38.79m/s、9.85m/s，即本文方法的整體重建效果顯著優于ART 算法和SART 算法。通過分析綜合運用以上兩個參數，可以進一步直接證明本文提出的方法在區域重建方面更具優勢。從數據整體重建的效果來看，TV-DL方法所獲得的結果與真實的模型小，三維重建的誤差遠比其他兩種算法小，綜合分析來看，在三維峰值超壓場重建模型的實際開發應用層面上，TV-DL方法的獲得三維重建模型效果最優。

5 結語

為得到爆炸沖擊波三維空間分布情況，并達到良好的可視化效果，首先本文深入研究了沖擊波二維走時層析成像的原理，在二維走時層析成像模型的基礎上，根據射線追蹤理論，構建起了三維沖擊波峰值超壓強場的重建模型；然后，運用了壓縮感知算法在稀疏約束方面的優點，給出了一種基于TV-DL 沖擊波超壓強場迭代修正算法；開展了模擬試驗，并對比了傳統重構算法ART、SART 和TV-DL 的重構結果。對試驗結論分析表明，本文首次提出的三維射線走時層析成像方法已經能夠初步實現三維沖擊波超壓場重建。TV-DL 修正代數重建精度的相對誤差基本保持在3%左右，與ART 算法相比，降低了5%左右，與SART 算法相比，降低了3%左右，本文僅對沖擊波三維重建進行了仿真實驗，但由于實際傳感器布設困難，后續會繼續研究在滿足重建精度的前提下減少傳感器個數，實現沖擊波三維重建。