基于變權(quán)TOPSIS模型的圍巖質(zhì)量評(píng)價(jià)方法研究*
王鳳山 錢 津
(陸軍工程大學(xué)野戰(zhàn)工程學(xué)院 南京 210007)
1 引言
圍巖作為支撐地下結(jié)構(gòu)荷載的主要成分,其質(zhì)量評(píng)價(jià)是工程界研究的熱點(diǎn)問(wèn)題[1]。圍巖受巖體結(jié)構(gòu)面、受力狀態(tài)、地應(yīng)力環(huán)境及開(kāi)挖擾動(dòng)等因素影響,易引起塌方、巖爆、涌水等工程災(zāi)害,有效把握圍巖自然屬性與工程特性,科學(xué)提取和分析圍巖質(zhì)量評(píng)價(jià)指標(biāo),是圍巖質(zhì)量評(píng)價(jià)的關(guān)鍵事項(xiàng)。
辨析圍巖變形與破壞的衍化機(jī)理和致災(zāi)過(guò)程,是解析圍巖質(zhì)量評(píng)價(jià)所要解決的核心節(jié)點(diǎn)問(wèn)題[2],全面考察影響圍巖穩(wěn)定性的多重要素,以期把握圍巖質(zhì)量評(píng)價(jià)中的模糊性、隨機(jī)性特征。以彌補(bǔ)常權(quán)決策的偏差為目標(biāo),變權(quán)TOPSIS 模型強(qiáng)調(diào)因素權(quán)重與因素狀態(tài)值的聯(lián)系、演變特征。集合TOPSIS[3]方法應(yīng)用于圍巖質(zhì)量評(píng)價(jià),尋求基于正、負(fù)理想方案間的一致和妥協(xié),以期提高決策結(jié)果的科學(xué)有效性。
2 圍巖質(zhì)量影響因素概述
圍巖有著穩(wěn)定性的系統(tǒng),但其同時(shí)還具有開(kāi)放性,根據(jù)位置和時(shí)間的不同而變化,遵循地表、地下等外力作用下圍巖地質(zhì)體系統(tǒng)物質(zhì)、能量和信息的交互機(jī)制和平衡作用,適應(yīng)量化評(píng)估圍巖質(zhì)量仿真推演的需要,從系統(tǒng)化角度建立影響圍巖質(zhì)量的結(jié)構(gòu)、要素、介質(zhì)的規(guī)范化描述[4],實(shí)現(xiàn)了影響圍巖質(zhì)量要素及指標(biāo)提取的一致性語(yǔ)義表達(dá),如圖1所示。

圖1 影響圍巖質(zhì)量要素描述
圖1中,圍巖質(zhì)量評(píng)價(jià)要素在結(jié)構(gòu)上反映評(píng)價(jià)模型的本質(zhì)思想和關(guān)鍵概念,是考察圍巖質(zhì)量整體作用體系的重要工具[5]。圍巖穩(wěn)定性受巖體質(zhì)量、完整程度、地殼外力等多種內(nèi)外因素的影響,對(duì)圍巖質(zhì)量評(píng)價(jià)要素的辨識(shí)和集合設(shè)計(jì),目的是構(gòu)建圍巖質(zhì)量評(píng)價(jià)模型的指標(biāo)體系,為質(zhì)量評(píng)價(jià)模型和系統(tǒng)分析建立基礎(chǔ),參考文獻(xiàn)資料和行業(yè)規(guī)范[6],選取6 個(gè)因素作為圍巖穩(wěn)定性評(píng)價(jià)的指標(biāo),分別為巖石抗壓強(qiáng)度(單軸)K1、巖石質(zhì)量指標(biāo)K2、巖體完整性系數(shù)K3、地下水發(fā)育狀態(tài)K4、巖體聲波速度K5以及結(jié)構(gòu)面走向與洞軸線夾角K6,建立指標(biāo)體系集合,K={K1,K2,……Kn},(1≤n≤6)。
3 指標(biāo)權(quán)重計(jì)算
3.1 熵值法計(jì)算指標(biāo)權(quán)重
熵值法[7]以原始信息作為數(shù)據(jù)支撐,是一種度量無(wú)序程度的客觀賦權(quán)方法。其中心思想是通過(guò)監(jiān)測(cè)各項(xiàng)指標(biāo)的變異程度來(lái)測(cè)算出指標(biāo)熵值的大小:熵值越大,反映出該指標(biāo)信息的不確定性越大,包含的信息越小;反之,熵值越小,則該指標(biāo)信息的穩(wěn)定性越好,相應(yīng)包含的信息越大。
1)設(shè)對(duì)m種方案si(1≤i≤m)構(gòu)成圍巖質(zhì)量方案集合S={si|1≤i≤m} 進(jìn)行對(duì)比評(píng)價(jià),結(jié)合n項(xiàng)指標(biāo)屬性構(gòu)成m×n原始數(shù)據(jù)矩陣,記作Smn={sij}m×n,即為
式(1)中,i表示評(píng)價(jià)方案數(shù)量,j表示指標(biāo)屬性個(gè)數(shù),sij為第i個(gè)方案第j個(gè)指標(biāo)值。
2)采取極差法對(duì)圍巖質(zhì)量評(píng)估原始數(shù)據(jù)矩陣Smn進(jìn)行標(biāo)準(zhǔn)化處理。結(jié)合式(2)、式(3)計(jì)算標(biāo)準(zhǔn)化矩陣S'。
圍巖質(zhì)量指標(biāo)呈現(xiàn)效益型特征時(shí):
圍巖質(zhì)量指標(biāo)呈現(xiàn)成本型特征時(shí):
3)根據(jù)熵值計(jì)算方法(4),圍巖質(zhì)量第i個(gè)要素指標(biāo)下Si的熵值為
式(4)中pui表示圍巖質(zhì)量第i項(xiàng)指標(biāo)下,第m個(gè)標(biāo)段的特征比重,則:
式(4)中,zi表示圍巖質(zhì)量各指標(biāo)要素的信息熵值,熵值越大,表示出圍巖質(zhì)量指標(biāo)體系的整體穩(wěn)定性越差,權(quán)重越小。至此,計(jì)算圍巖質(zhì)量評(píng)估指標(biāo)的權(quán)重αi為
式(6)中,0≤αi≤1,
3.2 變異系數(shù)法計(jì)算指標(biāo)權(quán)重
傳統(tǒng)熵值法僅依賴于數(shù)據(jù)本身的離散性,在測(cè)算權(quán)重時(shí)出現(xiàn)有的權(quán)重過(guò)大或過(guò)小的情況,對(duì)應(yīng)指標(biāo)數(shù)據(jù)為0 和1 時(shí)算出熵值均為0,很容易會(huì)造成關(guān)鍵信息的丟失。變異系數(shù)[8]是衡量方案中各個(gè)屬性值變異程度大小的統(tǒng)計(jì)值,變異系數(shù)法[9]則是通過(guò)計(jì)算各屬性在被評(píng)價(jià)對(duì)象上變異程度而得到權(quán)重的客觀賦值方法。
第一步:對(duì)第j個(gè)被評(píng)價(jià)屬性參數(shù)值求取均值和標(biāo)準(zhǔn)差σj:
第二步:計(jì)算第j個(gè)屬性指標(biāo)的變異程度γj:
第三步:計(jì)算出各項(xiàng)指標(biāo)的權(quán)重βj,通過(guò)對(duì)相應(yīng)指標(biāo)的變異程度進(jìn)行“歸一化”處理:
3.3 均值化計(jì)算指標(biāo)權(quán)重
考慮不同單一賦權(quán)法間偏差值較大,利用熵值法和變異系數(shù)法分別確定圍巖評(píng)價(jià)權(quán)重{αj}、{βj}(1≤j≤n),雖然消除了方案屬性量綱的差異,但也消除了各指標(biāo)變異程度上的差異,因此,通過(guò)引入均值思想[10]對(duì)指標(biāo)權(quán)重進(jìn)行平衡處理,具體如下:
式(10)中,ωj=a·αj+(1-a)βj,本文取a=0.5。
4 變權(quán)TOPSIS評(píng)價(jià)模型
TOPSIS 法[11]又叫逼近理想解的排序法,是經(jīng)典的多屬性決策方法。其中心思想在于:對(duì)方案進(jìn)行評(píng)價(jià)時(shí),首先計(jì)算出最佳方案和最差方案,即:評(píng)價(jià)問(wèn)題的理想解和負(fù)理想解,然后利用歐式距離計(jì)算法求出各指標(biāo)對(duì)象與正理想解和負(fù)理想解之間的貼近程度,進(jìn)而通過(guò)與理想解的相對(duì)貼近度對(duì)方案進(jìn)行排序和評(píng)價(jià),若評(píng)價(jià)對(duì)象距離正理想解最近且距離負(fù)理想解最遠(yuǎn),則為最佳方案,反之最差[8]。
但TOPSIS 方法[12]所采取的指標(biāo)權(quán)重基本上是由專家主觀確定的,其客觀準(zhǔn)確度較低。因此運(yùn)用均值化方法組合計(jì)算信息熵和變異系數(shù)法的指標(biāo)權(quán)值,取代了以專家經(jīng)驗(yàn)主觀上確定權(quán)重的方法,同時(shí)根據(jù)TOPSIS 法結(jié)合各指標(biāo)屬性的評(píng)價(jià)值[13],對(duì)最終的目標(biāo)方案進(jìn)行整體評(píng)價(jià)。
1)建立目標(biāo)方案評(píng)價(jià)模型的決策矩陣并進(jìn)行相應(yīng)的標(biāo)準(zhǔn)化處理,得到矩陣S,如式(11)。
2)根據(jù)確定的各評(píng)價(jià)指標(biāo)權(quán)重系數(shù),構(gòu)建加權(quán)標(biāo)準(zhǔn)決策矩陣U,如式(12)。
3)確定正理想值U+和負(fù)理想值U-,計(jì)算正、負(fù)理想值,如式(13)、(14)。
式(13)、(14)中,J+為效益型評(píng)價(jià)指標(biāo)集,J-為成本型評(píng)價(jià)指標(biāo)集。
4)求任一解yij到正負(fù)理想解的距離Li+、Li-,如式(15)、(16)。
式(15)、(16)中,u+、u-分別表示正負(fù)理想解的第j個(gè)分量。
5)計(jì)算各方案到理想解的貼近度Gi。
式(17)中,0≤Gi≤1,i=1,2,…,m。
6)根據(jù)相對(duì)貼近度Gi對(duì)各個(gè)方案進(jìn)行排序,選擇貼近度最大的方案為較優(yōu)方案。
5 模型計(jì)算
5.1 標(biāo)準(zhǔn)化決策矩陣
以地下洞室內(nèi)典型區(qū)域?yàn)槔鶕?jù)文獻(xiàn)[11]對(duì)4 個(gè)標(biāo)段內(nèi)圍巖穩(wěn)定性指標(biāo)為例,給出圍巖穩(wěn)定性樣本s1、s2、s3、s4的相關(guān)特征指標(biāo)取值,構(gòu)建地下洞室結(jié)構(gòu)的圍巖穩(wěn)定性質(zhì)量評(píng)價(jià)樣本集,其量化參數(shù)如表1。
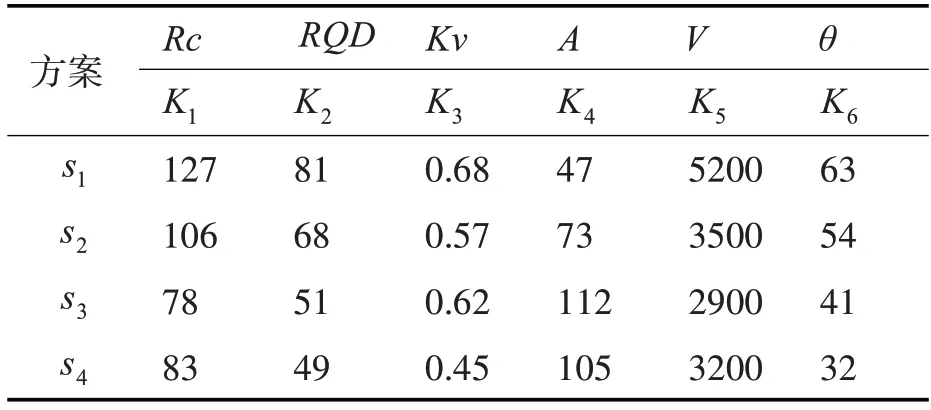
表1 圍巖穩(wěn)定性質(zhì)量評(píng)價(jià)樣本集
建立方案決策矩陣Y,利用式(11)對(duì)矩陣Y進(jìn)行規(guī)范化處理,則標(biāo)準(zhǔn)化矩陣S表示如下:
5.2 計(jì)算指標(biāo)權(quán)重
根據(jù)公式計(jì)算熵值法、變異系數(shù)法、均值化法下的指標(biāo)權(quán)重,具體如表2所示。
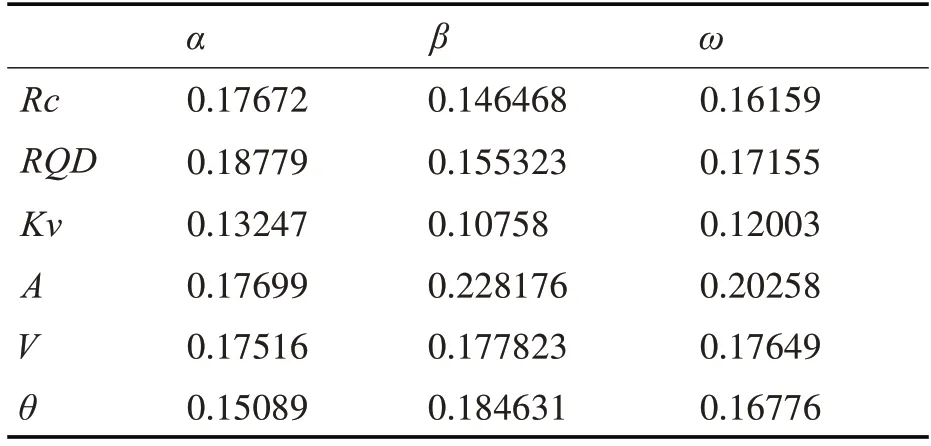
表2 圍巖質(zhì)量評(píng)價(jià)指標(biāo)權(quán)重
表2中,分別表示出三種方法下的指標(biāo)權(quán)重α、β、ω,并以此為數(shù)據(jù)支撐進(jìn)行各方案正、負(fù)理想解求解。
5.3 求解各方案正、負(fù)理想解
依據(jù)式(13)~(14)依次求得各方案正、負(fù)理想解,如表3所示。

表3 圍巖質(zhì)量評(píng)價(jià)方案正、負(fù)理想解
5.4 計(jì)算到正負(fù)理想解的距離
依據(jù)式(15)~(16)依次求得各方案到正、負(fù)理想解的距離,如表4所示。

表4 評(píng)價(jià)方案到正、負(fù)理想解的距離
5.5 計(jì)算相對(duì)貼近度并排序
根據(jù)式(17)依次求得各方案的相對(duì)貼近度G,如表5所示。
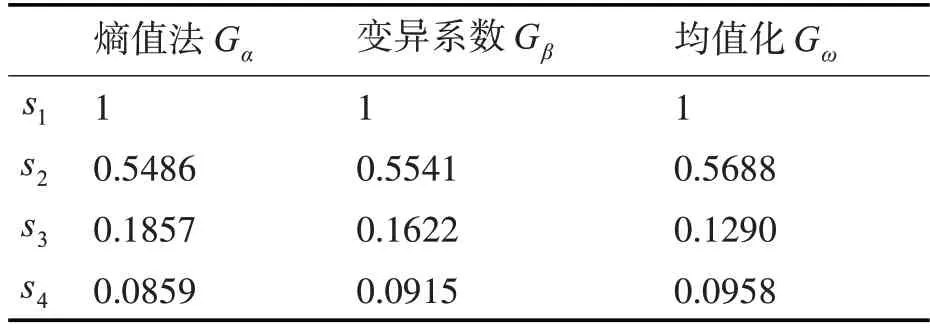
表5 圍巖質(zhì)量評(píng)價(jià)方案貼近度
5.6 模型效果分析
根據(jù)表5對(duì)圍巖質(zhì)量評(píng)價(jià)方案貼近度進(jìn)行排序,熵值法、變異系數(shù)法與均值化下的方案貼近度排序一致,結(jié)果為s1>s2>s3>s4。數(shù)據(jù)顯示,均值化作用后的圍巖質(zhì)量評(píng)價(jià)方案中,方案s2的貼近度高于常權(quán)作用下的方案貼近度,且方案s3、s4的貼近度更接近,對(duì)比工程實(shí)測(cè)數(shù)據(jù)更符合實(shí)際。通過(guò)貼近度大小排序可以清晰得出方案s1的圍巖質(zhì)量最好、穩(wěn)定性最高,對(duì)比工程實(shí)測(cè)結(jié)果一致,表明基于變權(quán)TOPSIS的圍巖質(zhì)量評(píng)價(jià)模型計(jì)算結(jié)果可靠,準(zhǔn)確性較高,具有較好的應(yīng)用價(jià)值。
6 結(jié)語(yǔ)
1)針對(duì)圍巖質(zhì)量評(píng)價(jià)的多指標(biāo)性,從系統(tǒng)化的角度提取影響圍巖質(zhì)量的各種因素,選取圍巖單軸抗壓強(qiáng)度、巖石質(zhì)量指標(biāo)、巖石完整性系數(shù)、地下水發(fā)育狀態(tài)、巖體聲波速度、結(jié)構(gòu)面走向與洞軸線夾角作為評(píng)價(jià)指標(biāo),構(gòu)建圍巖質(zhì)量評(píng)價(jià)模型[11]。
2)在評(píng)價(jià)過(guò)程中,采用熵值法、變異系數(shù)法對(duì)評(píng)價(jià)指標(biāo)進(jìn)行均值化賦值,克服了單一賦權(quán)法中指標(biāo)差異度較大、敏感性較強(qiáng)等特征對(duì)圍巖質(zhì)量評(píng)價(jià)結(jié)果的影響,增強(qiáng)了圍巖質(zhì)量評(píng)價(jià)模型的科學(xué)性、安全性。
3)以工程實(shí)例為數(shù)據(jù)支撐進(jìn)行仿真計(jì)算,在圍巖現(xiàn)地指標(biāo)測(cè)算值和方法算出組合權(quán)重值的基礎(chǔ)上,計(jì)算理性點(diǎn)貼近度與實(shí)例工程數(shù)據(jù)對(duì)比,結(jié)果表明基于變權(quán)TOPSIS的圍巖質(zhì)量評(píng)價(jià)模型得出的結(jié)論與實(shí)際結(jié)果一致,表明該方法、模型的合理可行。

