基于聲陣列炸點定位系統的時延判定算法研究*

王 琦 李 明 英俊杰

（西安工業大學電子與信息工程學院 西安 710021）

1 引言

炸點位置測試是常規靶場中重要的測試項目之一。利用爆炸時產生的聲信號正確估計出炸點的空間位置坐標，是炸點坐標測試技術中的關鍵環節。被動聲傳感器陣列定位技術成本低、隱蔽性強且可全天候探測，根據特定的幾何結構布置聲傳感器，采用時間差方法進行定位，即可探測到彈丸爆炸的位置信息［1］。爆炸聲通過聲波傳播時，近地炸點的爆炸物在膨脹過程中易受地面阻擋或山體、建筑遮擋，會形成混響，從而造成炸點信號識別困難［2］。聲傳感陣列定位技術中一般采用無線傳感器網絡，將具有無線通信功能的傳感器模塊搭載在聲傳感器上作為一個傳感器節點，通過信號處理方法對采集到的聲源信號進行處理，結合聲傳感器陣列的幾何結構得到目標的位置信息。并行分布式聲傳感器陣列利用各個聲傳感器所測聲源的目標信號，經過信號處理的方法計算出聲源的坐標［3～5］，僅在每個節點采用一個聲傳感器，因此分布式聲傳感陣列的計算復雜度要求不高，利于達到定位系統的實時實現。其中王洋等［6］提出基于時間差技術的五元十字陣算法，而本文選用的立體五元聲陣列較平面陣能給出更準確聲源三維位置。嚴天峰［7］結合接收信號自相關和互相關函數的特性，提出了基于二次相關的時延估計方法，減少了噪聲對互相關函數的影響。這些文獻所研究的方法對測量彈丸炸點參數具有推動作用，為了進一步提升彈丸落炸點參數精度，本文提出一種基于時延判定法的分布式聲傳感陣列炸點位置融合算法，研究一種存在混響時的炸點位置測試方法。

2 五元聲陣列探測模型的建立

本文構建的多聲傳感陣列彈丸炸點位置測試系統主要由五個相同的聲傳感器組成，其中五個聲傳感器呈正四棱錐分布。測試系統的工作原理為當彈丸在指定的探測區域爆炸時，會觸發聲傳感器采集炸點爆炸的聲信號。同時，根據五元聲陣列的空間布置關系，結合每個聲傳感器輸出炸點位置的時刻值，解算出彈丸炸點位置坐標為P(x，y，z)。如圖1所示五個聲傳感器呈正四棱錐分布，聲傳感器N0位于正四棱錐頂點處，其余四個聲傳感器分別分布在底面四個頂點，聲傳感器N1，N2，N3和N4沿逆時針方向分別放置，各個頂點到坐標系原點的距離記為D，聲傳感器N0的高度記為H。其中，N0，N1，N2，N3，N4為五個聲傳感器，則N0，N1，N2，N3，N4的坐標分別為(0，0，H)，(D，0，0)，(0，D，0)，(-D，0，0)，(0，-D，0)。

圖1 五元聲陣列炸點位置測試示意圖

為了方便計算彈丸炸點位置，假設在坐標系oxyz中的炸點位置為點P(x，y，z)，炸點P與每個聲傳感器的距離分別為r0～r4，每個聲傳感器N0、N1、N2、N3、N4捕獲的彈丸爆炸聲時刻分別記為t0、t1、t2、t3、t4，則爆炸聲信號到達N0與到達N1的相對時延為T0i=ti-t0，其中i=1，2，3，4，可獲得彈丸炸點位置與五個聲傳感器的時空函數，即：

式中，c為當前聲速。

同時，根據圖1可知，在坐標系oxyz中，炸點P相對于坐標原點O 的方位角為α，俯仰角為θ，彈丸炸點坐標P(x，y，z)的球面坐標系可表示為

結合式（1）和式（2），可以得到，方位角、俯仰角和探測距離的表達式為

將式（3）、（4）、（5）帶入式（2），可以解算出炸點P在坐標系oxyz中的位置信息。由式（3）～（5）可以看出，影響坐標測試的關鍵因素是時延值的獲取，所以能夠準確識別彈丸炸點的時刻值獲取到精確的時延值對系統的測試精度十分重要。

3 時延判定算法

對于任意兩路聲信號的時延差值可以采用廣義互相關法（Generialized Cross-Correlation）來估計一個信號達到兩個傳感器的時間延遲。假設兩個聲傳感器接收到的信號可以分別表示為x1(t)和x2(t)，兩路信號的廣義互相關函數Rx1x2(τ)等于互功率譜的傅里葉變換［8～10］，如下式表示：

其中，Gx1x2(ω)=x1(ω)x2*(ω)表示被測信號x1(t)、x2(t)的互功率譜密度函數；x1(ω)、x2(ω)分別表示聲傳感器N1，N2接收到信號x1(t)、x2(t)的傅里葉變換，*表示復共軛。

但在復雜背景的環境下，各類噪聲下的干擾容易引起互相關函數峰值變寬，出現假峰值。為了抑制噪聲的干擾，選擇在信號中加入加權函數，提高互相關函數的抗噪聲能力。在實際應用中，選擇合適的加權函數對GCC 函數的性能非常重要，本文經過對比之后選擇PHAT加權函數：

將PHAT 加權函數帶入式（6），兩信號的廣義互相關函數如下：

在高信噪比（SNR）的情況下，Rx1x2(τ)會得到明顯的峰值，但是存在混響以及噪聲信號與目標信號相似時［11～12］，PHAT 加權廣義互相關函數也會出現多個峰值的情況。除了在真實時延處出現一個峰值外，還會受到相似信號的影響在其他位置出現另外的峰值，其相關程度與相似信號的幅度大小有關。針對以上情況，同時考慮到聲源定位中無線傳感器網絡的特點，本文提出了一種時延判定算法，探討了在有混響的情況下，采用時延判決的方法對已經得到的時延值進行二次處理，該方法通過最小均方誤差準則在一組可能的TDOA 估計值中檢測出真實值，從而計算目標的聲源位置。

將五元立體聲陣列中聲傳感器N0為中心節點，其余四個聲傳感器節點以半徑為R的距離分布在中心節點四周。因為聲傳感器陣列有著特定的幾何結構，故任意兩個聲傳感器之間的真實時延差值與目標同傳感器節點之間的距離存在著嚴格的對應關系，而由混響產生的時延差值則不具有這樣的特性，即相關函數中虛假峰值，所以本文提出的時延判定算法如下。

根據經驗得出的信噪比選定閾值H，分別搜索相關函數R01(τ)、R02(τ)、R03(τ)、R04(τ)大于這一閾值時所對應時延的值。假設通過廣義互相關法每兩個傳感器得到的時延分別都存在n 個時延量，說明有虛假信號的出現。其R0i(τ)得到的時延分別為{ΔTi1，ΔTi2，…，ΔTin}，其中i=1，2，3，4。在四個集合中分別選取一個元素進行組合一共可以得到組時延向量，分別記為

其中，將A1，A2，…，Am稱為原時延向量組。

分別將以上的m組時延向量根據五元立體聲陣列炸點位置定位計算方法建立方程組求解目標位置，得到m個目標位置向量P1，P2，…，Pm。

用得到的目標位置向量計算時延向量為

其中，v為聲速，將τ1，τ2，…，τm稱為新時延向量，計算均方誤差：

其中使RMSE達到最小值時的m對應的Pm作為炸點目標的位置(x，y，z)。

本文提出的時延判定算法的流程圖如圖2所示，其基本思想就是只有真實的時延與目標同聲傳感器節點之間的距離存在嚴格的對應關系，而由混響和外界環境產生的相似信號得到的時延則不具有這樣的特性，所以當由虛假的時延得到的定位結果反演時延前后的均方誤差較大。而由真實時延得到的定位結果反演時延前后的均方誤差較小。當新時延向量均方誤差達到最小時的原時延向量即為真實的時延向量。因為在實際測試中，每個聲傳感器得到的原始聲信號進行相關函數運算中由于混響產生的尖峰數目不會很多，所以A1，A2，…，Am的值不會很大，整個過程的計算量也不會很大，所以具有實用價值。

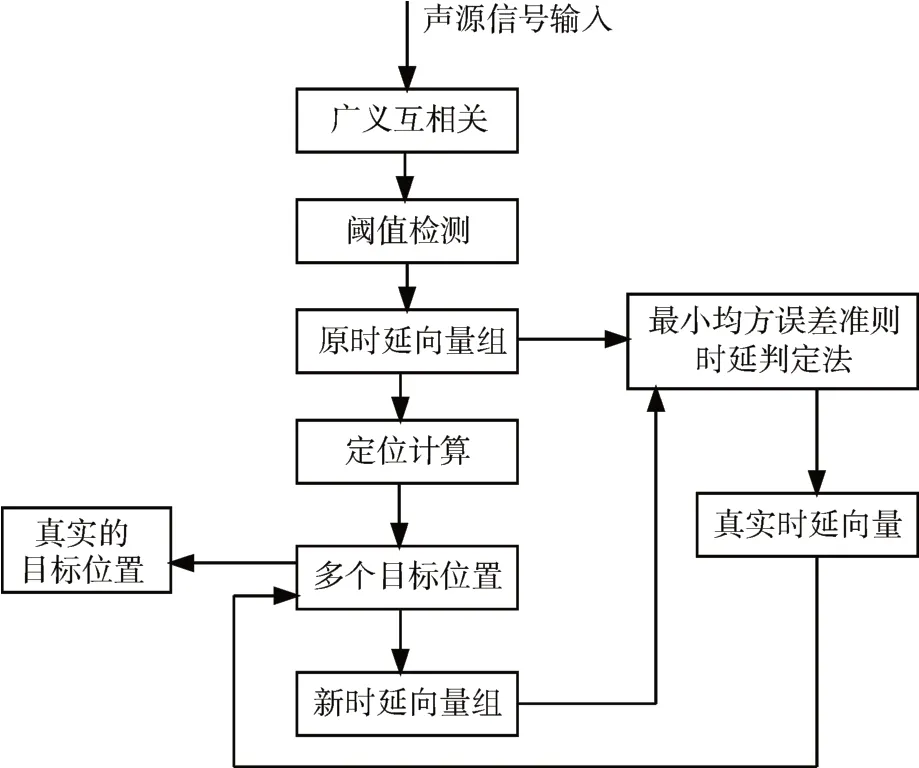
圖2 時延判定法流程圖

4 實驗與分析

為了評估基于時延判決準則的并行分布式融合算法在真實環境中的可行性，在空曠的室外進行測試，選擇無風的天氣進行實驗，測試出當時的聲速為c=341m/s。采用5個高精度聲傳感器按照第2 節建立的聲陣列炸點位置探測模型進行布置，其中，5個聲傳感器節點N0，N1，N2，N3，N4的坐標分別為(0，0，2)，(2，0，0)，(0，2，0)，(-2，0，0)，(0，-2，0)，單位為m。每個聲傳感器都設有獨立的采集裝置，采集裝置帶有同步觸發信號輸入端口和無線傳輸模塊。當彈丸爆炸后，聲傳感器開始采集聲信號，再由無線通信模塊傳送到終端處理計算機，終端處理計算機根據接收到的多路聲傳感器信號，經信號濾波處理和互相關函數法，提取各個聲傳感器輸出彈丸炸點聲信號的時延信息。

通過選取采集的語音信號，對其分別進行互相關算法和廣義互相關算法求取其時延值。五個聲傳感器對某一發爆炸聲音采集到的聲信號進行處理，采集到的炸點原始聲信號波形信號如圖3所示。

圖3 爆炸聲原始信號

當測試現場空曠無混響時，普通互相關法和廣義加權互相關法都可以得到準確的時延值，選取N0和N1聲傳感器進行互相關求解，得到的時延值為3.5ms，如圖4所示。由圖4也可看出，在現場環境中存在未知噪聲時，PHAT 加權的廣義互相關法比普通互相關法能更加明顯地獲取到波形峰值。

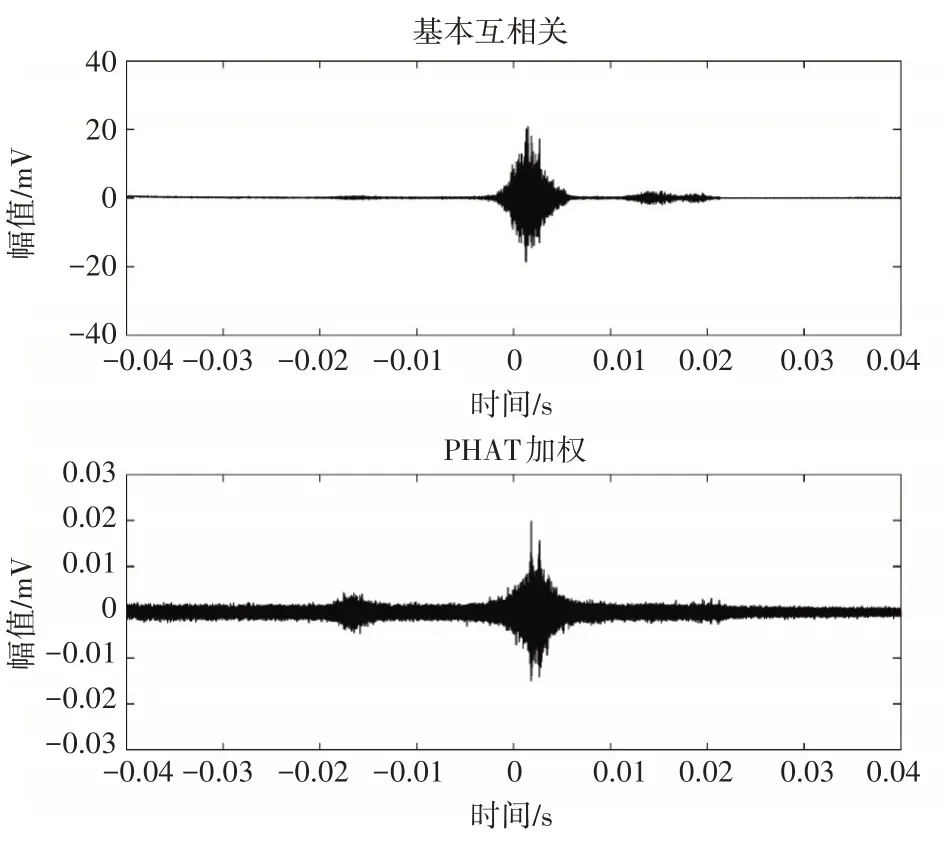
圖4 無混響時互相關結果

本文通過將某一路信號時延后模擬混響信號，得到帶混響的信號后，再次采用兩種相關函數法進行仿真，如圖5所示。從圖5中可以看出，普通互相關法和PHAT 加權法都得到了若干個峰值，此時無法分辨真正的時延。若再次用峰值檢測法獲取時延時會得到錯誤時延值，所以我們選擇獲取閾值H以上的時延值，采用時延判定法進行處理。

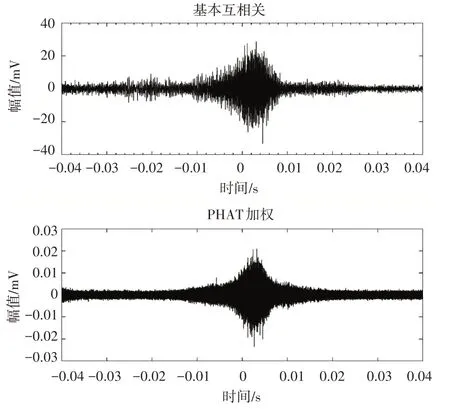
圖5 存在混響時的互相關結果

從上面的實驗結果中可以看出：在真實的測試環境中，由于環境因素的復雜，PHAT 加權的廣義互相關法比普通互相關法獲取的波形峰值更加明顯，更適合于獲取到準確的時延；而在存在混響及相似信號的影響下，PHAT 加權的廣義互相關法仍然比普通互相關法獲取的虛假峰值少，表明其濾除噪聲的性能更強，但其仍舊不能準確地獲取到時延信息，由此采用本文提出的時延判定法進行二次處理。

通過選取不同測量值時RMSE較小時的值，將該時延值作為分布式聲源定位的準確時延值。為了進一步驗證分布式時延判定法的可行性，本文對這發彈丸進行誤差計算。根據現場測定，爆炸聲位于P(8，7，2)處，依據本文提出的五元立體聲陣列炸點位置測試方法可知節點N0與節點N1，N2，N3和N4的真實時延向量為(3.5，2.9，-5.1，-4.6)，單位是ms，聲速c=338.9m/s。時延判定法的閾值為H=0.017，得到以下時延向量組：

R01(τ)={ΔT11，ΔT12}={3.5，3.2}，

R02(τ)={ΔT21，ΔT22}={2.9，2.5}，

R03(τ)={ΔT31}={-5.1}，

R04(τ)={ΔT41}={-4.6}。

分別將其排列組合成四組時延向量，即A1，A2，A3，A4，將其代入式（2）進行聲源定位，得到目標位置P1，P2，P3，P4。再利用得到的目標位置以及聲傳感器的位置代入式（1）重新計算時延得到新時延向量組τ1，τ2，τ3，τ4。原時延向量和新時延向量的均方誤差統計見表1。

表1 前后時延的均方誤差統計

根據表1可以看出，第一組原時延向量與新時延向量的均方誤差與其他組相比最小，僅為0.5，同時第一組就是真實時延向量組，而其它含有混響得到的時延向量組的前后時延的均方誤差均比真實時延向量組的大。仿真數據驗證了本文中提出的時延判定法的可行性與有效性。同時驗證了真實時延與目標同傳感器節點之間的距離有著嚴格的對應關系，而由混響產生的時延則不具有這樣的特性。所以當由虛假的時延得到的定位結果反算時延時前后時延誤差較大。而由真實時延得到的定位結果反算時延時前后時延誤差較小。以上分析說明，本文中提出的基于時延判定法的分布式聲傳感融合算法是可靠有效的。

5 結語

在聲陣列炸點位置測試方法中，互相關法由于其簡單實用具有廣泛的應用價值，但在存在混響或者相似信號的情況下，將很難獲取到準確的時延值，甚至會給出錯誤值導致炸點定位誤差極大。考慮到基于聲傳感器的無線傳感網絡這一領域，本論文以五元立體聲陣列為炸點測試基陣，運用廣義互相關法進行多彈丸爆炸聲信號的時延估計，采用時延判定法能夠在一組多個時延向量中判決出真實的時延向量，根據得到的真實時延向量計算出目標的真實位置。由于靶場的試驗環境存在多種隨機干擾因素，對強烈的外界干擾及相似信號的干擾本測試方法提出新的時延判定法為后續的炸點位置估計提供了很好的解決方案。