曲率障礙下四階變分不等式的交替方向乘子法*

張霖森, 程 蘭, 張守貴

(重慶師范大學 數學科學學院, 重慶 401331)

0 引 言

迄今為止,已有很多關于各種變分不等式問題的研究[1-6].但相對而言,關于曲率障礙的四階橢圓變分不等式問題的研究還不多[7-9].在這類障礙問題中,彈性膜在邊界固定和垂直方向受到外力作用與曲率障礙條件下,需要確定彈性膜的平衡位置.對于這類問題的數值解法,有間斷Galerkin方法[1]、有限元方法[3,7-8]、有限差分法[6].交替方向乘子法(ADMM)在結構優化問題中有著廣泛的應用,例如二維的變分不等式[10]、接觸問題[11-12]和Stokes問題[13].ADMM的每一次迭代,只需要求解一個線性問題,而且輔助未知量和Lagrange乘子是顯式計算的.對于任意的正參數,ADMM都是全局收斂的.但是該方法對罰參數非常敏感,很難根據具體問題選擇合適的罰參數.

本文重點分析了ADMM和罰參數的自適應法則求解關于單側曲率障礙四階變分不等式的組合算法[14-15].首先將ADMM應用于求解曲率障礙問題,由于ADMM的收斂速度嚴重依賴于罰參數,為了改進算法性能,我們提出了一種自適應法則,通過平衡原理和迭代函數來選擇合適的罰參數[16-17],然后得到了一種自適應交替方向乘子算法(SADMM),并分析了該方法的收斂性.最后給出了一些數值結果來驗證該方法的可行性和有效性.

1 單側曲率障礙問題的ADMM

本文考慮以下四階橢圓變分不等式問題:給定f∈L2(Ω),求解u∈K,使得

(1)

其中Ω是平面區域R2中的有界閉區域,其邊界為Г=?Ω,閉凸集

(2)

定義以下符號:

則問題(1)可以寫成如下變分不等式:求解u∈K,使得

a(u,v-u)≥l(v-u), ?v∈K.

(3)

由式(3)可知式(1)是一個變分不等式問題.則式(3)有如下性質:

其中C>0;

由于雙線性形式a(·,·)是對稱的,故變分不等式問題(1)等價于如下變分形式的極小值問題:求解u∈K,使得

J(u)≤J(v), ?v∈K,

(4)

其中

(5)

由式(1)、(4)和文獻[8]定義如下Lagrange函數L:H2(Ω)×(L2(Ω))2→R,

(6)

和函數空間

(7)

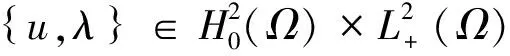
(8)

(9)

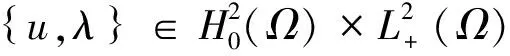
L(u,μ)≤L(u,λ)≤L(v,λ).

(10)

由式(10)中L(u,μ)≤L(u,λ)直接得到的結論(8),可以推出

Δu≤0, a.e. inΩ,

(11)

(12)

則

L(u,λ)=J(u).

(13)

在此基礎上,考慮增廣Lagrange乘子法.我們觀察到,問題(1)和(4)都等價于:求解{u,p}∈H,使得

j(u,p)≤j(v,q), ?{v,q}∈H,

(14)

其中

(15)

(16)

對于ρ>0,由增廣Lagrange乘子法

定義

(17)

接著定義

(18)

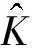
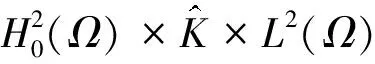
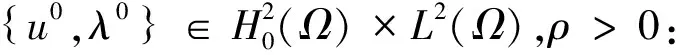
求解pn+1∈L2(Ω),使得

Lρ(un,pn+1,λn)≤Lρ(un,q,λn), ?q∈L2(Ω).

(19)

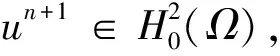
(20)

更新Lagrange乘子,得到

λn+1=λn+ρ(Δun+1-pn+1).

(21)

在這種方法中,最小化問題(19)中的pn+1可以由un和λn顯式求解.最小化問題(20)形成一個變分問題,對于給定的λn,pn+1和ρ>0,該變分問題具有唯一的解.因此,我們得到下面的ADMM[10,16].

算法1(ADMM)

第二步 計算輔助變量pn+1∈L2(Ω),

(22)

(23)

第四步 更新Lagrange乘子

λn+1=λn+ρ(Δun+1-pn+1).

(24)

2 單側曲率障礙問題的SADMM

對于算法1,我們注意到它對于任何固定參數ρ>0都是無條件收斂的.然而,如果參數太小或太大,該方法的效率將大大降低.為了改進ADMM的性能,我們提出了一個可變參數ρn的自適應規則.下面我們假設一個非負序列{sn}滿足

(25)

在此基礎上,我們提出SADMM,具體算法過程如下[11].

算法2(SADMM)

第二步 計算輔助變量pn+1∈L2(Ω),

(26)

(27)

第四步 更新Lagrange乘子

λn+1=λn+ρn(Δun+1-pn+1).

(28)

第五步 選取罰參數,使得

(29)

關于算法2中第五步罰參數的選取將在算例分析部分詳細說明.為了證明算法2的收斂性,需要如下的基本結論.

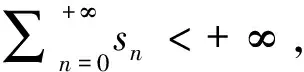
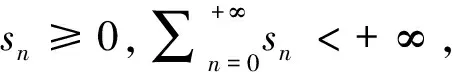
定義以下符號:

根據問題的性質和算法的原理,可得算法2的收斂性結果.

定理1 設{un,pn,λn}是算法2產生的序列,則

(30)

其中p=Δu.

證明令δun=un-u,δΔun=Δun-Δu,δρn=ρn-ρ,δλn=λn-λ.由式(9)和(23),有

在以上兩式中取v=δΔun+1,將它們相減得到

a(δun+1,δun+1)=(δλn+ρn(Δun+1-pn+1),-δΔun+1),

(31)

在式(31)中,用p=Δu,我們得到

a(δun+1,δun+1)=(δλn+ρn(δΔun+1-δpn+1),-δΔun+1).

(32)

根據式(28),有

δλn+1=δλn+ρn(δΔun+1-δpn+1).

(33)

從引理1的式(11)和(12),有λ≥0,-Δu≥0,且在Ω上(-Δu,λ)=0,因此可以得到

ρn(-Δu,(λn+ρnΔun)+-λ)≥0,

(34)

又有

(λn+ρnΔun-(λn+ρnΔun)+,(λn+ρnΔun)+-λ)≥0.

(35)

結合式(34)和(35),有

(λn+ρnδΔun-(λn+ρnΔun)+,(λn+ρnΔun)+-λ)≥0.

再根據式(26),可得到

(-ρn(Δun-pn+1)+ρnδΔun,δλn+ρn(Δun-pn+1))≥0,

因此

(36)

根據式(28),可得到

δλn+1-ρnδΔun+1=δλn-ρnδΔun+ρn(Δun-pn+1).

最后,由式(36)得到

因此,該定理得證.

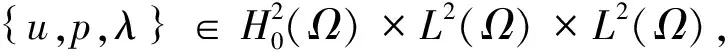
證明根據sn≥0,0≤ρn+1≤(1+sn)ρn和式(33),有

(37)

將式(30)代入式(37),有

(38)

由式(33)和(38),可得

(39)

即存在一個常數C>0,使得對于任意的n≥0,有

(40)

根據式(38),我們也可以得出

(41)

由式(33)、(40)和(41),有

因此

(42)

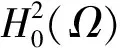
(43)

因為p=Δu,再結合式(43),可以得到

(44)

因此,在L2(Ω)上,pn→p.

對于?n≥1,由式(39),有

(45)

根據式(33)和(45)可知{λn}是有界的,可得λn→λ.

注1 在算法2的第五步中令sn=0,有ρn=ρ0,則算法2中罰參數為固定參數,即為算法1,從而可以得算法1也是收斂的.

3 算 例 分 析

本文利用自適應交替方向乘子算法求解四階單側曲率障礙的變分不等式問題,迭代過程中通過迭代函數自動調整罰參數,用變參數ρn代替ρ,從而達到提高算法效率的目的[2,10,13].下面具體考慮算法2(SADMM)中選擇罰參數ρn的自適應法則.根據算法的收斂性證明式(30)知下式成立:

‖λn+1-λ-ρn(Δun+1-Δu)‖≤‖λn-λ-ρn(Δun-Δu)‖.

利用平衡加快收斂,我們希望

‖λn-λ‖≈‖ρn(Δun-Δu)‖.

使用以下方法來確定合適的參數ρn,給定常數μ>0,如果

‖λn-λ‖>(1+μ)‖ρn(Δun-Δu)‖,

那么在下次迭代的時候要增加ρn;如果

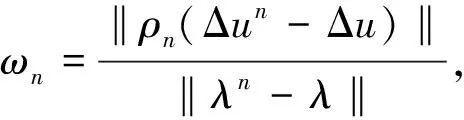
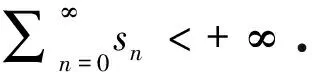
用cn計算ρn改變的次數,令c0=0,則

采用如下方法得到非負序列{sn}:

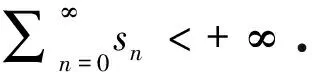
為了檢驗本文算法的可行性,這里根據具體的算例進行數值分析.考慮一個具體的障礙問題:求解u∈K,使得

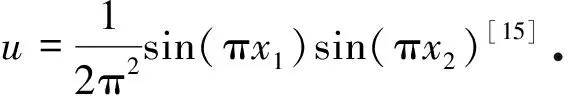
采用本文的ADMM 和SADMM兩種方法進行求解,取步長h=1/40和參數ρ=1,u和-Δu的數值解結果如圖1和圖2所示,解析解如圖3所示,圖4為逐點誤差,可見數值解和精確解是吻合的.

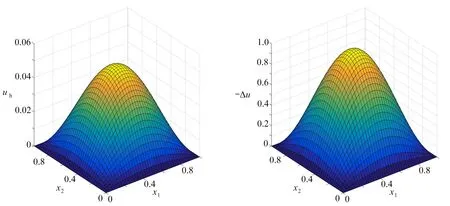
圖1 u的數值解 圖2 -Δu的數值解

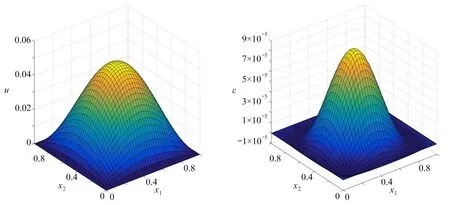
圖3 精確解u 圖4 逐點誤差

對于不同的初始罰參數取值ρ,表1分別對步長h=1/10,1/20,1/40,1/80時ADMM和SADMM所需的迭代次數進行了比較,表中*表示迭代達到了最大迭代次數200后即停止.表2分別給出了迭代所需的CPU運行時間,單位為s.表1和表2的結果表明,SADMM不僅有效減少了迭代次數,收斂速度更快,而且很穩定.SADMM的收斂速度和CPU運行時間受初始參數ρ的影響很小.

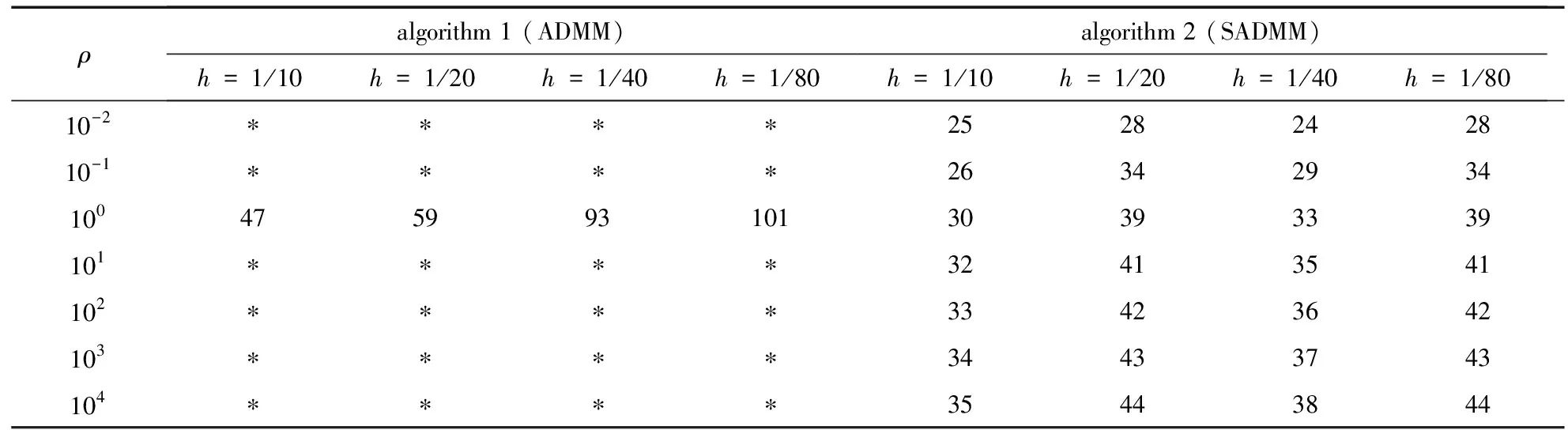
表1 算法隨步長變化所需迭代次數的情況

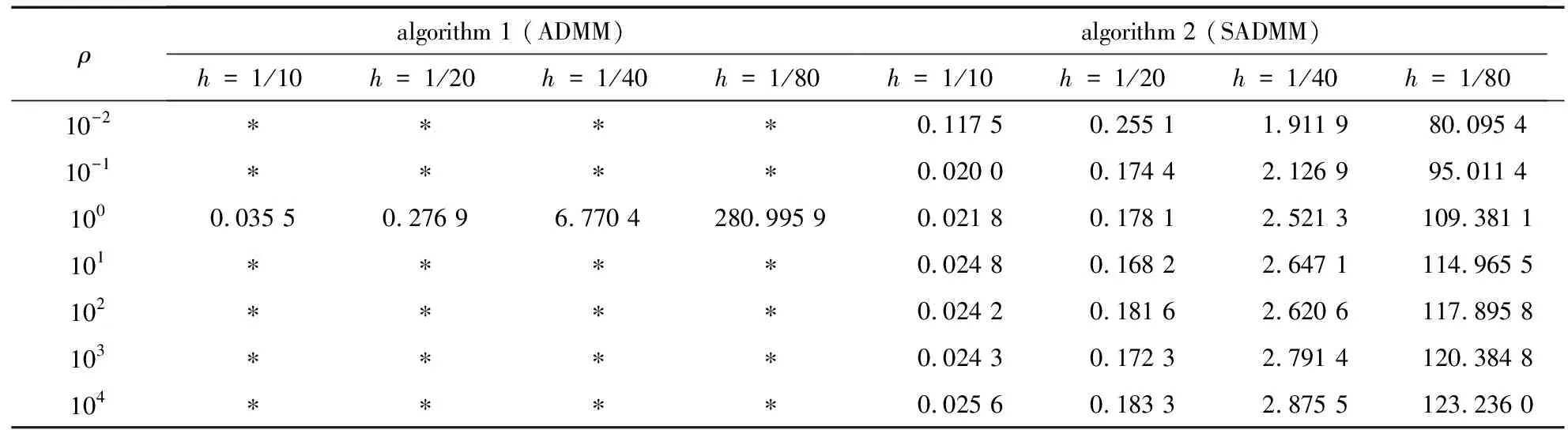
表2 算法隨步長變化所需CPU時間情況

4 結 論

本文提出了求解四階單側曲率障礙變分不等式問題的SADMM.先引入輔助函數和Lagrange函數,將問題轉化為鞍點問題,使用ADMM求解.為了提高計算效率,通過平衡原理和迭代函數,迭代過程使用自適應法則選取合適的罰參數.數值算例的結果表明,參數對SADMM影響較小,該方法加快了收斂速度,且較為穩定.該方法還可以推廣到四階雙側曲率障礙問題的數值求解中.

致謝本文作者衷心感謝重慶師范大學教學改革研究項目(xyjg007;sz202114)對本文的資助.