立足結構化教學優化題組設計

陳明珠

數學知識是有結構的，數學教學也是有結構的，實現教學結構化，可以助力學生知識、方法和思維的有效建構，結合教學實踐，教師立足結構化教學，從這四個方面優化題組設計：固點（理解知識點的本質）、串線（大單元整合成一條清晰的知識線）、組面（單元與單元延伸成知識模塊）、成體（構建小學生的知識結構體系），將學生的知識結構體系進行優化，培養學生擁有一個完整的結構化思維，達到培養學生數學核心素養的教學目標。

認知心理學家布魯納曾經說過一句話：“已經掌握的知識，如果沒有經過結構進行完美的聯系，隨著時間的推移就會變成被人所遺忘的知識。”小學數學結構化教學，是指教師站在系統的高度，從整體的角度出發，針對學習的發生以及過程進行審視，以此來對學生的結構思維進行培養，形成“帶的走”的學習方法和能力。“題組”能夠做到的就是將內容、形式、思維方法、解法相似的題目結合在一起組成一個組題。筆者通過實踐發現只要立足結構化教學，從固點、串線、組面、成體這四個方面優化題組設計，就可以優化和完善學生的知識結構體系，推動學生結構化思維的飛速發展，進而達到提高學生數學核心素養的教學目的。

一、立足結構化教學的生長點 ，優化“固點”題組設計

新課標指出，數學的結構化教學是一個整體，它的生長點指的是每個“碎片化”的單一的知識點，而“固點”就是在每一章節的學習、小結中，結合教材的知識點，從多角度、多方面，針對概念、意義以及知識點進行深入了解，并進行分析和總結。要透徹理解知識點的本質，而不僅僅停留在知識的表面。只有鞏固好每個知識點，才能進行知識間的溝通和關聯，這樣結構化教學才有生長的力量，因此我們要立足結構化教學的生長點 ，優化“固點”題組設計。牢牢地掌握知識點，為學生學習數學知識打下堅實的基石，從而進一步提高學生的學習質量以及學習能力。

例如，教師進行“圓柱的表面積”這一節課的結構化教學時，側面積公式就是結構化教學的生長點，只有扎實的掌握了側面積公式，才能靈活解決有關于圓柱表面積的實際問題，做好知識間的溝通和串聯，因此筆者設計了以下的“固點”題組，力求讓學生深刻理解并掌握圓柱的側面積就是底面周長×高。

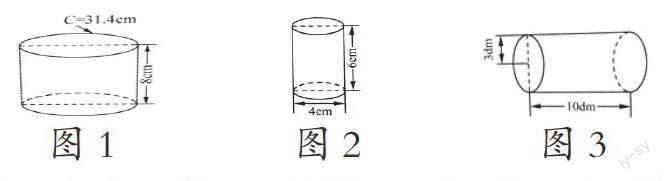
固點題組：求以下圓柱的側面積。

第一題是已知底面周長和高，求圓柱的側面積（如圖1），第二題是已知直徑和高，求圓柱的側面積（如圖2），第三題是已知半徑和高，求圓柱的側面積（如圖3）。它們內在聯系為圖2將圓的直徑轉化為圓底面周長，圖3將圓的半徑轉化為直徑，再轉化為底面周長，從而求圓柱的側面積。

通過以上練習，厘清 “已知圓柱的半徑、直徑、底面周長，求圓柱的側面積”三種題型之間的內在聯系。都是要把它轉化成底面周長，通過底面周長×高，求出側面積。學生就在腦海里的認知結構中存入了“已知底面周長和高求圓柱的側面積”這個固點，像這樣抓住概念本質，優化“固點”題組的設計，有利于學生及時鞏固理解知識本質，觸類旁通，舉一反三。因此，在教學每一節新課時，都要牢牢抓住該章節的生長點，優化“固點”題組設計，領悟知識的本質，扎實的掌握生長點，提高學習效率，優化學生的認知結構。

二、立足結構化教學的整合點，優化“串線”題組設計

結構化教學的核心就是整合，將知識點與知識點溝通、串聯起來，用結構化的思維對單元知識、方法、思維進行整合，指導學生從碎片的學習到整體的學習，整體性越強、概括性越強，就越有利于學習的保持和遷移。因此在整合時不能僅僅是簡單知識點的羅列，而是要優化“串線”題組設計，所謂的“串線”題組就是從單元整體的視角，將零散的知識點放到整個單元知識的結構當中，引導學生整理清楚知識脈絡。有助于學生厘清單元各知識間的內在聯系，縱向整合成一條系統的、明確的知識線，為結構化教學整合提供保障，從而構建學生新的認知結構，實現思維的拔節、提升。

例如，在“圓柱和圓錐”這一單元的結構化教學中，包含的知識有圓柱的特征、表面積和體積，圓錐的特征和體積等比較碎片的知識點，因此筆者立足“線”的構建，系統地將這些知識進行整合，優化設計了以下的“串線”題組：

一做。用一張長30㎝，寬20㎝的長方形紙疊出了一個圓柱。想一想，圓柱與長方形各部分之間有什么聯系？什么變了？什么沒變？

二思。制作無蓋圓柱體形狀的水桶需要多少鐵皮是求什么？

三算。一個圓柱體的底面半徑為2㎝，高為8㎝，它的表面積為多少？

四切。①把底面直徑為20㎝，高為8㎝的蛋糕從沿底面垂直切成2半，什么變了，什么沒變？如果沿底面垂直切成N半呢？②把底面直徑為20㎝，高為8㎝的蛋糕平行于切成2段圓柱，什么變了，什么沒變？那如果平行于底面切成N段呢？

五涂。同學們如果要在這個雙層蛋糕的表面部分（如圖4），涂上一層厚厚的奶油，但是下底面不涂，你們知道涂奶油部分的面積是多少嗎？

六挖。為了做造型，陳老師在這個直徑為20㎝，高8㎝蛋糕里挖了一個直徑為10㎝，高2㎝的圓柱（如圖5），需要涂奶油（底面不涂）的面積是多少㎝2？

七伸。為了做造型，從棱長為10㎝的蛋糕中挖走了一個直徑為3㎝，高為6㎝的圓柱，剩下的蛋糕是多少m3？

八變。一塊圓柱形的橡皮泥，底面積是12㎝2，高是5㎝，如果把它捏成等底的圓錐，這個圓錐的高是（? ? ），如果把它捏成等高的圓錐，這個圓錐的底面積是（? ? ）。通過做（復習圓柱的特征及由來），思（復習表面積的概念），算（數形結合復習表面積兩種計算公式），切（復習表面積的變化），通過涂和挖（復習整體求表面積的方法，并對比發現不管是涂N層還是挖N層都是求一個大的圓加幾個側面積），再通過伸（拓展了圓柱的體積），最后通過變（復習圓錐的體積）等一系列的練習將碎片化知識進行整合，以知識的由來、運用、拓展的順序為線，串成一條完整的單元知識鏈，像這樣優化“串線”題組的設計，使學生對“圓柱和圓錐”這一單元知識的認識從零散到條理，從模糊到清晰，從清晰到深刻，便于學生更深層次理解知識脈絡，掌握學習方法，積累學習經驗，從而建構了新的認知結構，因此在教學單元知識完后，教師要立足結構化教學的整合點，抓住本單元的核心知識點，優化設計一系列的“串線”題組，將知識點由點延伸成線，讓學生觸到知識的本質，從而提高學生的學習效率，進一步打開學生的眼界和思路。

三、立足結構化教學的聯結點，優化“組面”題組設計

結構化教學強調聯結點即教師要深入研讀教材，挖掘單元與單元之間相關知識、方法、思維等內在關聯和異同之處，并將其聯結起來，從而展開結構化、科學化、系統化的教學，加深學生對知識含義的掌握，構建一個屬于自己的數學網絡圖，同時也培養了學生認真仔細的觀察能力以及自由發揮的想象力，有效提高了學習效率。因此我們可以立足結構化教學的聯結點，優化“組面”題組設計，所謂的“組面”題組即打破常規單元內的知識梳理，找到聯結點重組關聯，將分散在各單元有聯系的、相關的，本質是一樣的知識點，通過對比、聯想、歸納等方法進行橫向整合，形成“知識面”。這樣的“面”相較于“線”，更能讓學生理清知識盲點，觸及知識的本質，使知識更加系統化，從而完成模塊知識的構建，為結構化教學的實施搭建了有力的橋梁，實現學生認知的升華。

例如，分數乘法、分數除法、比和百分數的應用題，他們零散的分布在六年級上冊，但知識聯系密切，他們的聯結點是本質一樣，都是分數乘除法應用題，用的線段圖也一樣。因此筆者優化設計了如下的“組面”題組：

一編。你們能根據下面的線段圖編一道乘除法應用題嗎？（如圖6）

二解。①一條路長1000米，工程隊已修了全長的1/4，還剩多少米沒修？②一瓶牛奶，喝了300毫升，已經喝了1/4，這瓶牛奶一共多少毫升？③一本書有100頁，看了和未看的比是1∶3，看了多少頁？④一條泳道已經游了100米，是全長的25%，全長是多少米？

三比。比一比，這些題目有什么共同點，把你的發現寫下來。

一編：先讓學生根據線段自主編題，引導學生使用數形結合來理解知識的本質；二解：通過對學生編的不同題目進行分類整理，比如第一類是分數乘法，單位“1”已知，量和率不對應，第二類是分數除法，單位“1”未知，量和率對應，第三類是比的應用題，但是比可以轉化成分率，單位“1”已知，量和率也對應，第四類是百分數的應用題，也可以轉化成分率，也是單位“1”已知，量和率對應的問題。三比：學生通過自己分析，溝通聯系，得出分數、比、百分數應用題，他們都是分數乘除法應用題。當單位“1”已知時，用單位“1”×對應分率＝對應量，當單位“1”未知時，對應量÷對應分率＝單位“1”。這樣從“線”聯結成“面”，既復習了舊知，也形成了新的知識網，建構了新的數學模型，有助于數學方法的運用、數學思想的產生，因此，在教學中可以立足于結構化教學的聯結點，優化“組面”題組設計，注重單元知識之間的聯系，抓住聯系設計“組面”題組，對單元與單元的知識進行分析、比較、歸納、總結，實現練一組題，通一類題，從而“把書越讀越薄”，數學思維更加深刻。

四、立足結構化教學的落腳點，優化“成體”題組

結構化教學的落腳點是幫助學生形成結構化的知識與技能和結構化的思想與方法。《義務教育數學課程標準（2022 年版）》針對數學基礎知識的教學明確提出，教師要對數學課本進行熟練的掌握，不管是什么學段的學生都要有對課本局部的理解，同時，對整個小學階段的數學課本要有全面的掌握，從而構建一個整體的結構化教學，有助于學生構建屬于自己的知識網絡。因此可以立足結構化教學的落腳點，優化“成體”題組設計，所謂“成體”題組是將知識點放到每個學段，乃至整個小學數學體系的知識結構上，從整體上把握知識結構設計題組，了解知識的產生和發展以及知識背后蘊藏的思維和內涵，從點—線—面—體感受知識之間的關聯性，最終將知識與技能、思想與方法融為一體，從而實現結構化教學，完善學生的認知結構，形成結構化、一體化、系統化的知識體系。

例如，在結構化教學“長方體、正方體、圓柱和圓錐等立體圖形的表面積和體積”時，其落腳點是溝通這些立體圖形的表面積和體積之間的聯系，統一成同一個計算方法，促使學生對立體圖形的認識進一步系統化、一體化，因此筆者設計如下“成體”題組：

1.基礎題：你能完成下面的表格嗎？

2.綜合題：你能自己探究出正三棱柱、正五棱柱等的表面積和體積嗎？

以上題組涵蓋了長方體、正方體、圓柱、圓錐、三棱柱、五棱柱等的表面積和體積。首先通過對長方體、圓柱等已學的表面積和體積公式的梳理，激發學生的原有經驗，通過綜合題拓展探究正三棱柱、正五棱柱等的表面積和體積，從而通過觀察、對比、分析等構建小學階段完整的立體圖形表面積和體積的知識體系，發現所有直柱體的側面積都是“底面周長×高”（圖7），表面積都是“側面積＋兩個底的面積”，體積都是“底面積×高”圖8，讓學生對立體圖形進行系統化的認識，了解知識與知識之間存在的關系，豐富完善學生的認知結構。

小學的知識具有“螺旋上升”的特點，每一年所學的新內容，都是前面基礎的深化，越來越復雜、越來越抽象，從而形成完整的知識體系。實踐也證明，學生大腦比較容易記住的是一定范圍內各種關系、框架和體系，因此，我們可以立足結構化教學的落腳點，優化“成體”題組，將知識點放進學段里甚至整個小學階段，做到心中裝綠洲、眼中看森林，助力學生逐步構建每個知識體系，對知識形成整體的結構化認知，促進結構化教學。

五、結語

總之，我們要在結構化教學的基礎上，尋找知識與知識之間存在的聯系，優化設計“固點→串線→組面→成體”的題組，將碎片化的知識連成線、結成網、筑成塊、構成體，不斷對知識進行系統的總結、消化、提煉、升華，有助于學生學習能力的大幅度提升，以及將知識點、學習方法和思維方式進行結構化建構，推動學生結構化思維的發展，進一步提高學生的數學核心素養。