心“中”有“線”　筆下有路

吳佑泉

為有效減輕義務教育階段學生過重的作業負擔，落實“雙減”政策，2021年4月，教育部辦公廳印發了《關于加強義務教育學校作業管理的通知》，著力健全作業管理機制，嚴控書面作業總量，要堅持以習近平新時代中國特色社會主義思想為指導，全面貫徹黨的教育方針，落實立德樹人根本任務，堅持以學生為本，強化學校教育的主陣地作用，大力推進學校減負提質工作，做強做優校內教育，提升作業設計質量，探索分層作業、個性化作業、有效作業等實施途徑，健全教育良好形態，促進學生全面發展、健康成長。

加強學校作業調控，督促各地各校落實作業管理通知要求，制定完善作業管理辦法，有效控制作業量和時長，特別是數學作業要做到精選、精練，要讓學生的知識系統得到夯實和擴充，要讓學生的做題水平得到質的飛躍，做到減量不減質和減而不簡，不做重復性和機械性作業，把體力勞動變成腦力勞動，要讓學生對數學產生熱愛，發揮學生的主觀能動性，主動探索數學難點，培養學生的“五大”核心素養，從橫向上擴大知識面，從縱向上研究知識的本質，從事物的表象到內部的本質和規律，深刻地領會數學知識的重要性。

努力提高課堂教學質量，堅持“兩個”并重，“減負”和“提質”兩手抓、兩手都要硬，做到持之以恒、久久為功。兩者是相輔相成的、密不可分。“減負”，學生的作業量少了，重復和低等的學習，使學生的認知水平和素質結構沒得到提高；“提質”通過“題海戰術”，只能增加學生的做題經驗，讓學生的知識面得到擴大，單純從橫向發展，縱向得不到加深，學生的數學核心素養得不到有效提高。

“雙減”要求作業能夠靈活設計，選題更有代表性，精選題型，滿足不同學生的學習需要，達到減負、提質、增效的目的。本文從中點為切入口，把初中階段的中點知識形成一個知識體系，層層深入，融合數學知識點和圖形的直觀性，培養學生思考的維度，提高書寫方向。

傳統教學是“只見樹木不見森林”，我們要走向關聯、重整體的教學。傳統教學是分—總式學習，大單元教學是總—分—總式學習，課前老師把握課標，駕馭教材，分析學情，敘寫目標，基于大單元進行知識建構、情境建構、主題建構，這是關鍵，讓所教所學知識點具有系統性、關聯性、遞進化、科學化，即最小的課程單位。

串聯式復習不僅可以減輕學生學習負擔，以核心知識為載體，培養學生學科思想和方法，以及核心素養，指向學生遷移應用知識和解決問題的能力，而且還把知識點進行區分、對比、深度加工，讓學生思維得到提升，使學生形成知識間的豐富聯系，建立良好的認知結構，使教學內容“結構化、一體化、網絡化”。

中點在華師大版初中數學各冊中都有出現，是初中數學教學中不可缺少的知識點。在七年級上冊中，中點出現在線段中點，主要考查學生對線段的計算，初步認識中點的意義，讓學生感受數形結合思想；在七年級下冊中，學生從線到封閉圖形的發展，從一維上升到二維，學習三角形的中線，為計算三角形面積和三角形全等，以及研究等腰三角形提供知識基礎；在八年級上冊中，學生研究等腰三角形的性質“三線合一”，即底邊的中線和高、頂角的平分線；在八年級下冊中，為深入研究特殊四邊形的幾何性質提供思路，結合平面直角坐標系點坐標的中點坐標公式，倍長中線的思想為作輔助線解決問題提供突破口；在九年級上冊中，研究三角形的中位線、重心及其性質和在直角三角形中斜邊上的中線的性質；在九年級下冊中，研究圓中的垂徑定理和弧的中點的性質。

在不同的環境中起到的作用也不同，主要涉及三角形、四邊形和圓，在考試中，特別是中考經常出現數學中點問題，因此探索此類中點問題的解題規律對初中幾何的學習有著十分重要的意義，可以培養學生數形結合的思想。

一、中點在三角形中的性質及其運用

初中階段主要研究的圖形是三角形，幾何教學中有兩大基本元素：角和線段，中點主要涉及解決線段問題，再推廣到其他問題，如面積、周長等。

（一）三角形的中線

幾何語言：在三角形ABC中（如圖1），D為BC的中點，則BD=BC，s△ABC=s△ACD=1/2s△ABC證明性質成立中，要體現三角形等底同高的數學思想方法。

例1? 在三角形ABC中（如圖2），D是BC中點，E是AD中點，且三角形ABC的面積為24cm2。

求三角形BEC的面積。

分析思路：

首先，計算面積，但未知高，突破口在三角形的中線;其次，AD、BE、CE分別是△ABC邊BC上的中線、△ABD邊AD上的中線、△ACD邊AD上的中線;最后，三角形BEC的面積與三角形ABC的面積的關系。

（二）等腰三角形的“三線合一”

因為等腰三角形的軸對稱性，則有等腰三角形的頂角平分線、底邊上的中線、底邊上的高在同一條線上，簡稱等腰三角形的“三線合一”。

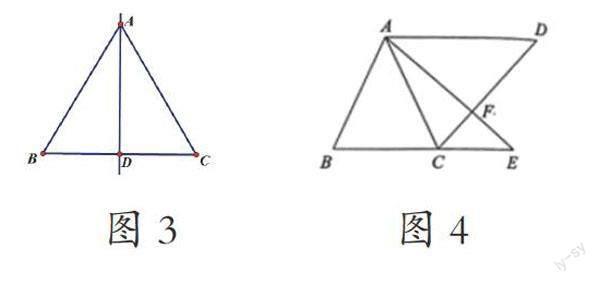
幾何語言：在等腰三角形中（如圖3），AD所在直線是三角形的對稱軸，則有：AD平分∠BAC，AD⊥BC，AD是邊BC的中線。

例1：如圖，AB=AC，作三角形ADC，使得點B、D在AC異側，且AD=CD，∠ADC=∠BAC，E是BC延長線上一點，連接AE交CD于點F，若AB2=2CF·AD，試判斷三角形ACF的形狀，并說明理由。

分析思路：

首先，△ABC和△ACD都是等腰三角形;其次，分析AB2=2CF.AD，由線段比例關系猜想出兩個相似三角形：△ABC相似于△ACD，列出對應邊成比例，得出BC=2CF;其次，從等式的特點思考：BC=2CF，由等腰三角形“三線合一”可知，過點A作AH垂直于BE交BC于點H；最后，在證明△AHC全等于△ACF，得證三角形ACF是直角三角形。

學生在分析問題時，要突破兩點：等式的運用和輔助線。學生從已知分析，會感覺“山重水復疑無路”，只要把AH畫出來，思路就豁然開朗，整道題的思路就“柳暗花明又一村”，有利于提高學生分析已知的能力。

（三）直角三角形斜邊上的中線

在直角三角形中，兩個銳角互余和邊長滿足勾股定理外，還有其邊角關系，斜邊上的中線也有特殊性。在直角三角形中，斜邊上的中線等于斜邊的一半，且是直角三角形外接圓的半徑。

幾何語言：在直角三角ABC中（如圖5），∠C=90°，D為斜邊AB邊上的中線，則AB=2CD（證明此定理，采用倍長中線）。

例1：如圖6，在正方形ABCD和正方形CEFG中，點D在CG上，BC＝1，CE＝3，H是AF的中點，求CH的長。

思路分析：

首先，找到含CH的三角形，連接AC和CF；其次，由勾股定理求AC和CF；最后，在直角三角形ACF斜邊上中線CH的性質，求CH的長。

（四）三角形的中位線及其重心

三角形的中位線平行于第三邊，并且等于第三邊的一半。

幾何語言：在三角形ABC中（如圖7），EF是三角形ABC的中位線，則EF∥BC，BC=2EF 。

例1：如圖8，在邊長為8的等邊△ABC中，D，E分別為AB，BC的中點，EF⊥AC于點F，G為EF的中點，連接DG，求DG的長。

思路分析：

首先，連接DE，構造三角形DEG；其次，DE是三角形ABC的中位線；最后，在Rt△EFC中，求出EF的長。在Rt△DEG中，再由勾股定理求出DG；在同一個三角形的兩條邊上分別取中點，構造中位線，既有數量關系，也有位置關系。

例2：如圖9，在Rt△ABC中，∠ACB=90°，AC=6，點D是斜邊AB的中點，點G為△ABC的重心，DG=2，求BC的長。

思路分析：

首先，由三角形的重心性質可知，CD：DG=3：1，求出CD的長；其次，AB=2CD；最后，在Rt△ABC中，再由勾股定理求出BC。

二、中點在四邊形中的性質及其運用

四邊形各邊的中點連線四邊形，簡稱中點四邊形，主要運用三角形中位線的性質，培養學生知識遷移的能力，以及轉化思想，把未知條件轉化為已知條件，讓知識點貫穿在一起，形成一個整體和體系，體現單元整體教學。

例：在四邊形ABCD中（見圖10），E、F、G、H依次是邊AB、BC、CD、DA的中點，連接EF、FG、GH、HE形成四邊形EFGH，求證：四邊形EFGH是平行四邊形。

思路分析：

中點主要出現在三角形中，所以連接AC，形成三角形ABC和三角形ACD。

首先，EF和HG分別是△ABC和△ACD的中位線；其次，AC是兩個三角形的公共第三邊；最后，EF平行且等于HG，得出四邊形EFGH是平行四邊形。

小結：

若四邊形ABCD是矩形，則中點四邊形EFGH是菱形；若四邊形ABCD是菱形，則中點四邊形EFGH是矩形。

三、中點在圓中的性質及其運用

垂徑定理? 垂直于弦的直徑平分這條弦，并且平分這條弦所對的兩條弧。

幾何語言：在○O中（如圖11），直徑CD⊥弦AB，則有AB⊥CD，弧CA=弧CB，弧DA=弧DB。

例1：如圖12，⊙O的直徑AB和弦CD相交于點E，AE=2cm，EB=8cm，∠DEB=60°，OF⊥CD于F．求CD的長。

思路分析：

首先，由垂徑定理得CD=2DF；其次，連接OD，在Rt△ODF中，只需已知OF和半徑OD；最后，OF在Rt△OEF中，利用銳角三角函數可求，再由勾股定理求出DF。

四、結語

在圓中，由直徑所引發的兩種數量關系和一個位置關系：平分弦、平分弧、垂直弦，知其一，便可得二。此性質在解決圓中的弦、弦心距、拱高、半徑等計算時，將圓中的問題劃歸到特殊三角形（等腰三角形、直角三角形等）問題。

這幾個性質相互聯系，再做出合理的輔助線，放“中點”歸圖，在中點問題教學中，要培養學生的觀察能力，提高學生的圖形結合能力，培養學生的分析能力與概括能力，并幫助學生實現知識之間的聯系與轉換，從而提高學生的綜合分析問題和概括問題的能力。

注：本文系鯉城區教育科學“十四五”規劃課題（第一批）2021年度課題“基于核心素養下初中數學校本作業有效性研究”（項目編號：LCJG145-157）研究成果之一。