邊坡滑坡安全狀態的評判標準研究

黃 兵

（遵義市交通勘察設計有限公司，貴州 遵義 563126）

0 引言

在實際邊坡工程中，易受到外部荷載和人為因素的影響而發生邊坡失穩破壞，對人民安全和財產造成損失。因此，對邊坡穩定性的研究和判斷一直是工程領域的重點。

李騰[1]根據某邊坡實際工程案例，采用坡面修整和錨桿格柵的方式對邊坡加固的施工方法進行研究。趙輝等[2]考慮到了降雨的影響，模擬了強降雨條件下邊坡飽和滲流的時程變化情況，探究了邊坡安全系數與土體飽和度之間的關系和變化規律。徐小樂等[3]研究了牽引式滑坡在暴雨、地震等不離條件下的失穩概率。熊楊福[4]利用實際工程土樣進行了不同含水率下的膨脹力試驗，推導邊坡受到膨脹力作用的穩定性分析表達式。

該文為研究邊坡滑坡在自然災害和人為因素影響下的破壞情況，對在滑坡過程中的累計位移-時間關系和St-t關系進行理論研究和梳理，對比了理論和實際的差異。對滑坡的4 種變形階段進行劃分，推導出加速變形階段與急劇變形階段之間的臨界點劃分標準。

1 滑坡變形曲線

圖1 為在塑性累計破壞中的經典滑坡表面時間-位移曲線。從圖中可以看出，在開始階段，滑坡受到外部荷載（地震、強降雨、列車）和人為因素擾動發生初始變形，位移增加速度較為緩慢。在勻速變形階段，累計位移增加緩慢，相對來說比較穩定。在勻速變形階段末端和加速變形階段開始時，位移-時間曲線出現拐點，位移增加速度逐漸加快。最后在急劇變形階段，邊坡出現較大的變形，開始出現失穩。

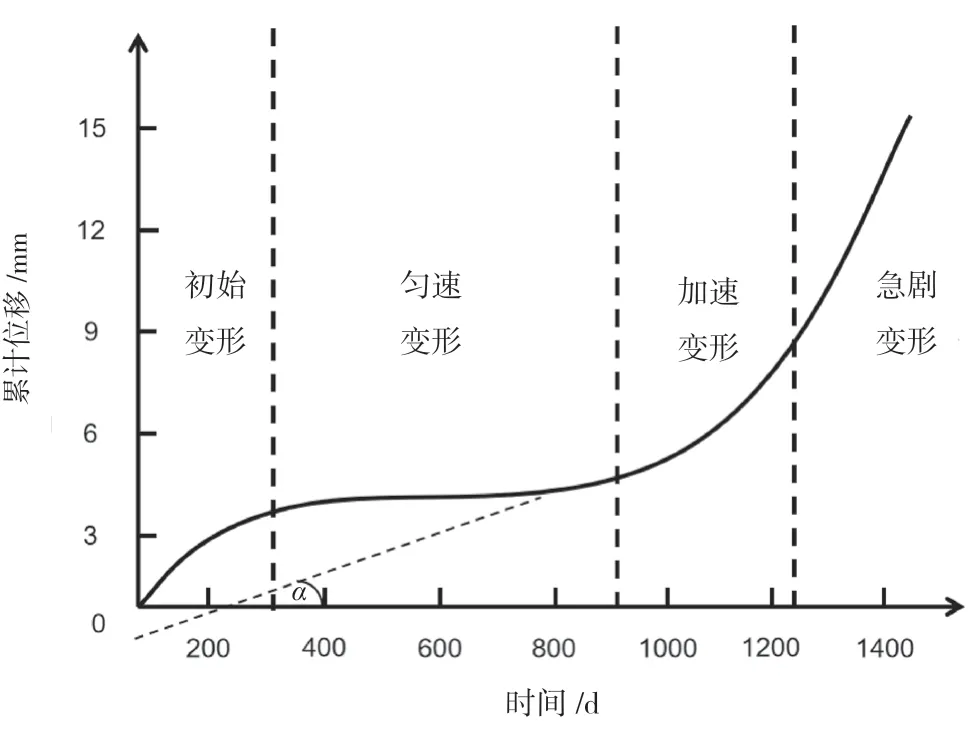
圖1 滑坡累計時間-位移曲線

將累計位移/時間定義為St，即在t時刻該點對應的原點坐標割線正切值。圖2 為滑坡割線斜率-時間曲線，從圖2 得知，St=tanα，表示在圖1 累計時間-位移曲線中該點連線坐標原點的連線與水平橫坐標軸的夾角，因此該St-t曲線反映了在累計時間-位移曲線中的割線正切值隨著時間的變化趨勢。

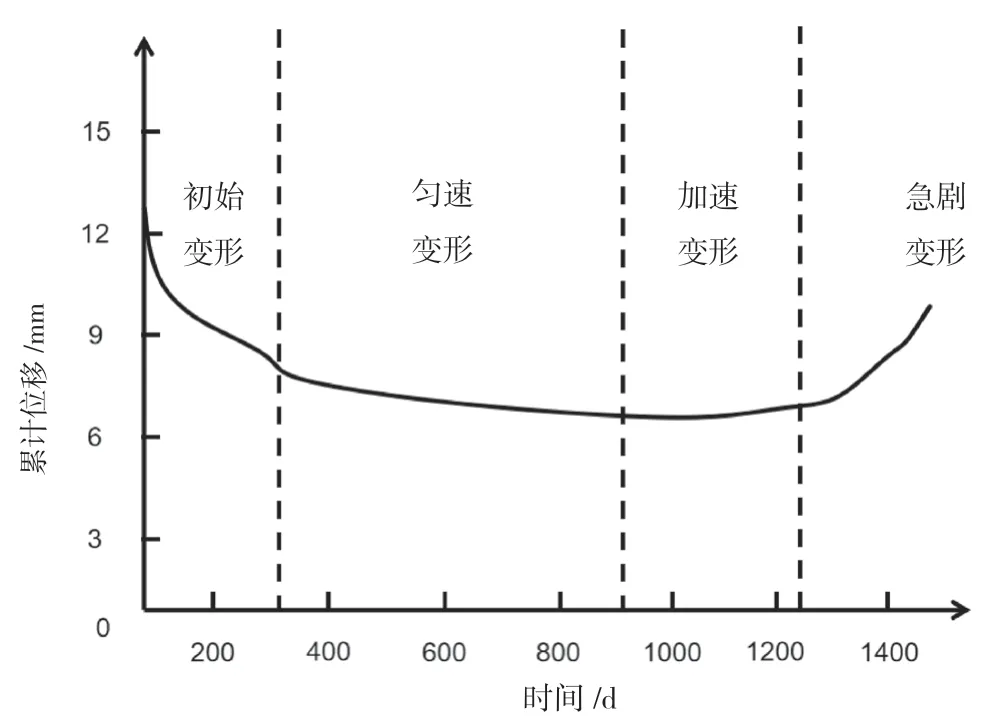
圖2 滑坡割線斜率-時間曲線

如果該曲線囊括邊坡從初始階段直到最后急劇變形發生失穩破壞，St-t曲線具有以下3 種特征：1）在1 初始變形階段，St呈現下降趨勢，斜率小于0。2）在1 勻速變形階段，St下降幅度微小，斜率逐步由負轉變到0 附近。3）在3 加速變形階段，St呈現開始逐步增加，斜率由0 變正。4）在4 急劇變形階段，St呈現快速增長的趨勢，邊坡開始出現過大的變形，進而出現失穩破壞的情況。

然而在實際邊坡檢測過程中，很難從初始變形階段監測，很可能在某一特定變形階段進行監測，這時的St-t曲線則與圖2 所呈現的存在差異。圖3 為不同變形階段的累計位移-時間曲線和St-t曲線。

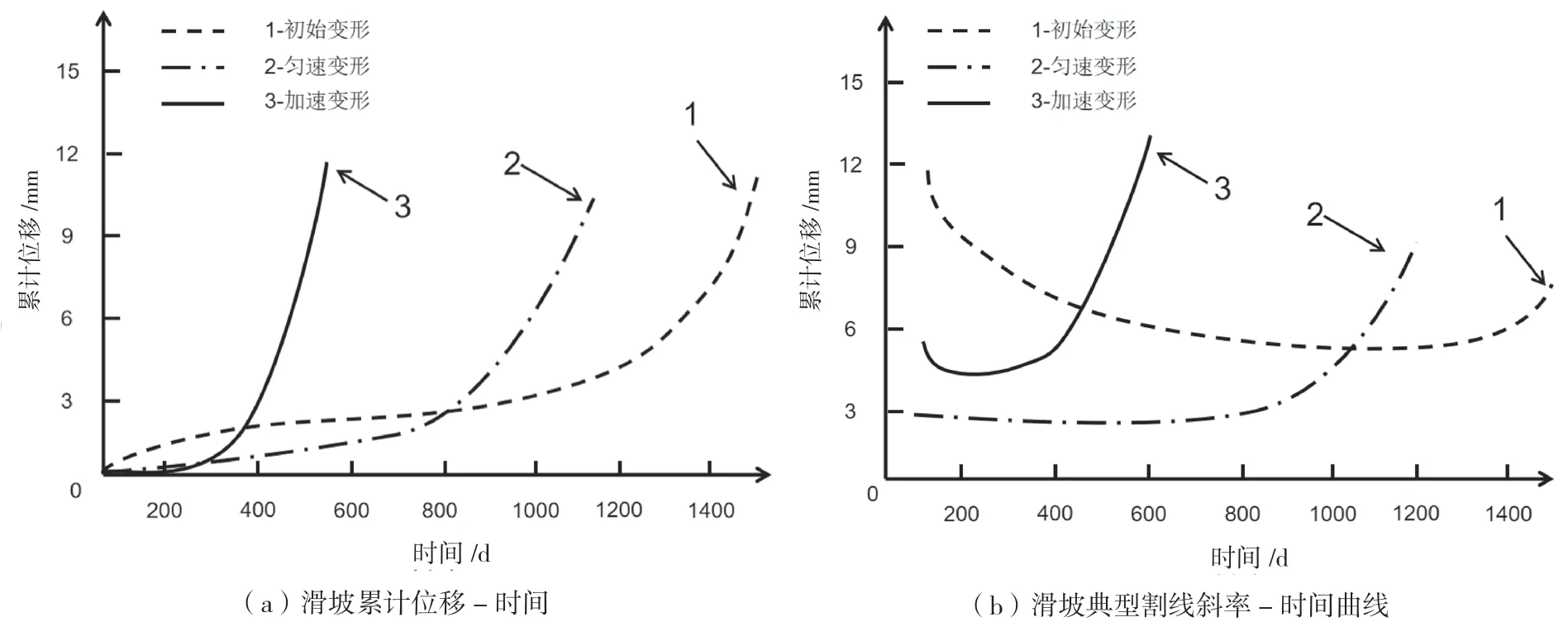
圖3 邊坡變形曲線

2 滑坡變形的St-t 曲線

在實際的滑坡案例中，由于受到許多外界因素的影響，因此在實際監測過程中不可避免地存在操作和設備上的誤差，滑坡變形的監測數據和St-t曲線很少呈現該文所描述的那種趨勢。

為了進一步對滑坡的變形規律進行探究，并由此獲得St-t曲線對滑坡進行分析和預測，該文采用間距為勻速階段1/20 時間段作為間隔的方式采用等間距描點法做出滑坡的位移-時間曲線。

2.1 案例1

案例1 為受人為因素影響導致的基巖滑坡，St-t曲線如圖4 所示。在初始變形前期，曲線波動較大，St從0.3 升至0.6，然后經過一段微小波動后開始變小。在勻速變形階段，曲線較為平穩，斜率逐漸變小，在末段接近于0。在加速變形階段，St開始逐漸上升，斜率越來越大，最后進入急劇變形階段，St和斜率都出現較快地增長，邊坡開始破壞。

2.2 案例2

案例2 為鐵礦附近的巖質滑坡，圖5 為案例2 的滑坡St-t曲線。在初始變形階段，案例2 與案例1 相近，曲線波動較大，St從1.3 升至2.6，然后經過一段波動后開始逐漸變小。在勻速變形階段，案例2 與案例1 不同，St下降幅度較大，最后加速度逐步遞增，到達急劇變形階段。

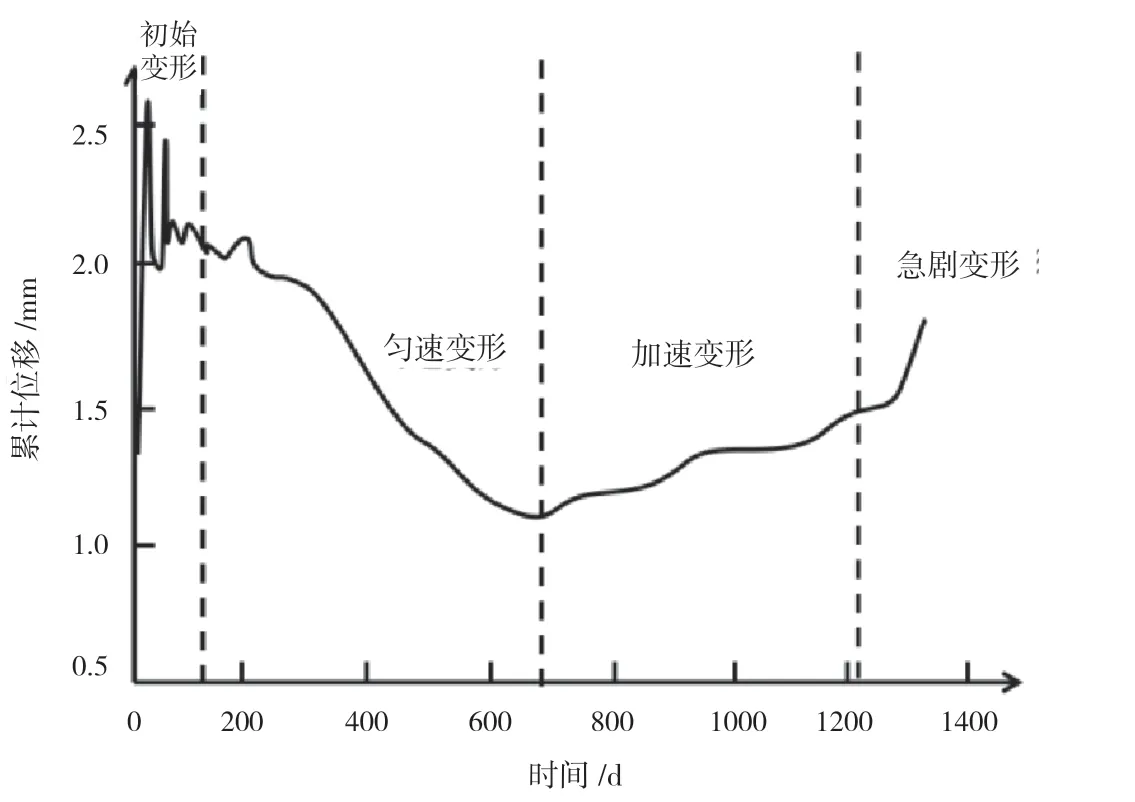
圖5 案例2 滑坡St-t 曲線

2.3 案例3

圖6 為案例3 的滑坡St-t曲線。該曲線與案例1 和案例2 略有不同。從圖中可以看出，隨著時間的增長，逐步從勻速變形階段到加速變形階段，這期間St數值變化不大，直到加速變形階段末期，St才開始增長，然后進入急劇變形階段，斜率越來越大。

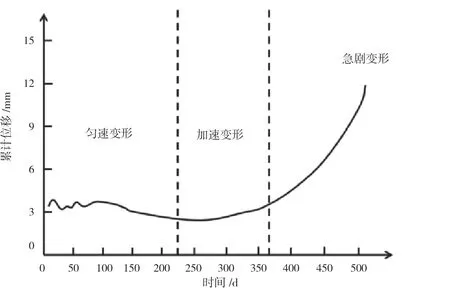
圖6 案例3 滑坡St-t 曲線

2.4 案例4

圖7 展示了案例4 的滑坡St-t曲線。該案例相對較為經典，經歷初始變形、勻速變形、加速變形和急劇變形4 個階段。在初始階段末到加速變形階段末，曲線較為平穩，然后進入急劇變形階段。

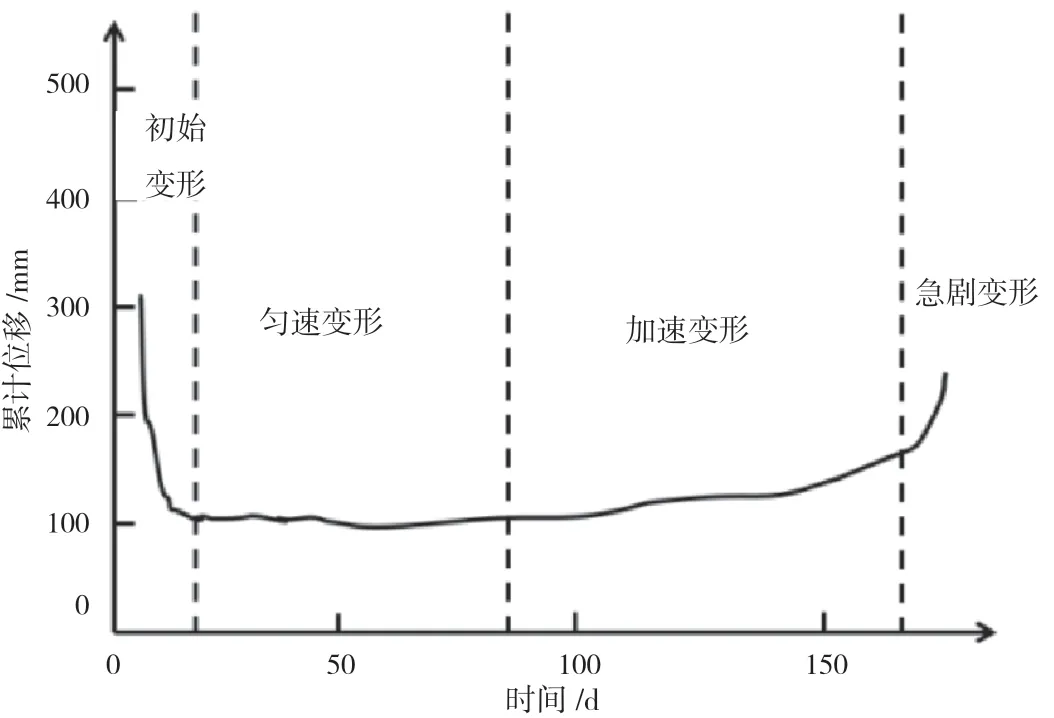
圖7 案例4 滑坡St-t 曲線

3 滑坡各階段判斷標準

為了便于實際工程施工和應用，更準確地對滑坡進行預測，對滑坡St-t曲線中的初始變形、勻速變形、加速變形和急劇變形4 個階段劃分標準進行確定。

當St-t曲線在起始階段時，斜率為負數且數值較大，則可由此判定該滑坡處于初始變形階段。

當斜率為負數但數值較小，曲線St數值緩慢下降，則可由此判定該滑坡處于勻速變形階段。

當斜率開始緩慢地由負轉為正，曲線St數值開始上升且上升趨勢逐步加快，由此判定該滑坡處于加速變形階段。由于斜率取值較為困難，需要進行擬合，實際工程中難以采用，因此通過公式（1）進行判斷。

式中：λ為該曲線的割線斜率；ti為在i時刻的時間；Sti為i時刻累計位移與時間的比值。

滑坡預警關鍵是判斷滑坡是否從加速變形階段到達急劇變形階段。常規方法一般是對一些物理量進行整合來進行判斷，如速率、加速度、位移量等。由于在實際工程中滑坡地質的復雜性和易受到人為、自然因素的影響，傳統的方式復雜且不實用。

經過對上述4 個案例的研究并且對相關文獻進行閱讀歸納，總結相應的判斷依據。通過5 期割線斜率和當期割線斜率進行計算的1 個以上割線斜率比判斷較為可靠。表1 為采用該方法進行滑坡加速變形階段與急劇變形階段之間臨界點的相關數據。

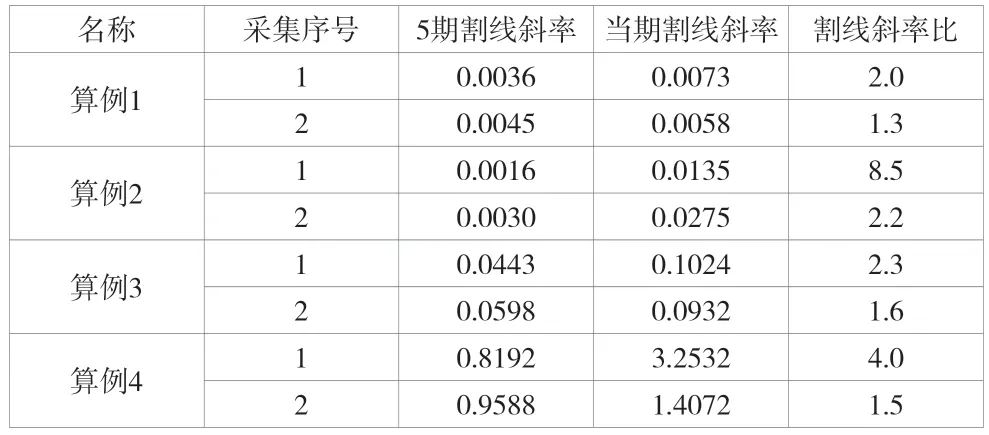
表1 滑坡割線斜率

從表1 的滑坡割線斜率比可以發現，曲線位于滑坡加速變形階段與急劇變形階段之間臨界點附近時，割線斜率比由連續兩期采集的，前一期大約在2.0～3.5，占66%，后一期割線斜率比約在1.2～2.0，占66%。為盡量避免滑坡危害，因此將第一期割線斜率比2.0，第二期割線斜率比1.0 作為臨界點，如果大于該數值就認定滑坡變形增速過大開始進入急劇變形階段。

根據以上標準，對以上案例滑坡進行判定預警，表2 展示了各滑坡利用該標準的報警次數。從表2 可以看出，4 種算例中，報警次數普遍為1～2 次。該預警方式較為準確，比較符合實際情況。因此，判斷邊坡是否開始進入急劇變形階段進而發生失穩破壞，該標準是較為實用的。

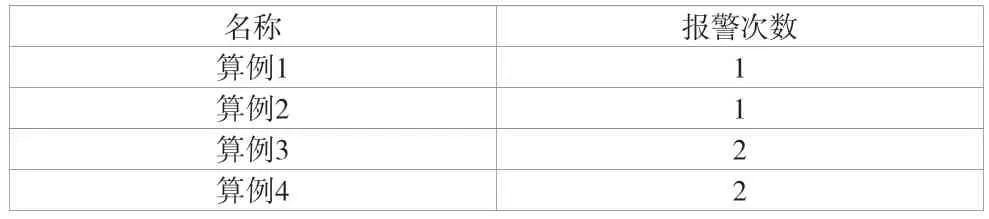
表2 各算例報警次數

4 結論

該文對在滑坡過程中的累計位移-時間關系和St-t關系進行理論研究和梳理，并根據不同的算例，對比了理論和實際的差異。對滑坡的四種變形階段進行劃分，推導出加速變形階段與急劇變形階段之間臨界點劃分標準，結論如下。

在開始階段，滑位移增加速度較為緩慢，斜率逐漸減少。在勻速變形階段比較穩定。在勻速變形階段末端和加速變形階段開始時，位移-時間曲線出現拐點。急劇變形階段，邊坡出現較大的變形，開始出現失穩。

土體本身存在不均勻性和各向異性等特點并且在實際監測過程中的誤差，實際滑坡變形的監測數據和St-t曲線與理論存在較大差異。

基于4 種算例驗證，通過5 期割線斜率和當期割線斜率計算的兩個以上割線斜率比來對加速變形階段與急劇變形階段之間臨界點進行判斷的方法較為可靠。