基于自抗擾對電磁耦合調速器的轉差控制研究
謝鼎盛,儲江偉,李 紅,張澤涵,劉梓敬
(東北林業大學 交通學院, 哈爾濱 150040)
0 引言
電磁耦合調速器是一種依靠磁拉力傳遞動力的裝置,在工業領域應用廣泛。但由于電磁耦合調速器機械特性較軟[1],增加負載時,轉速迅速下降,扭矩變化明顯,功率損失增大。PI雙閉環的控制策略,可通過人工控制的方法強化電磁耦合調速器的機械特性,提高輸出轉速的穩定性[2-3],但仍存在很大的優化空間。進一步對控制的優化需要先對電磁耦合機構的動力學特性與電磁轉矩進行模型分析[4-6]。
線性自抗擾控制(line auto disturbance rejection control,LADRC)算法是一種具有良好控制性能的算法[7-8],能夠實時估計并補償系統收到的不確定性干擾,借助反饋環節達到優于傳統PID算法的控制性能[9-11]。對于LADRC的研究,文獻[12-13]運用級聯擴張器的自抗擾技術,提高了永磁電機矢量控制系統的可靠性和對外界干擾的魯棒性。文獻[14]通過LADRC提高了永磁同步電機的魯棒性,優化了控制效果。文獻[15]通過自抗擾算法對步進電機進行控制,有效降低了步進電機中的扭矩脈動。文獻[16]針對電動汽車的穩定性,利用自抗擾技術提高了電動汽車的駕駛平順性。文獻[17-18]在對直線感應電機的控制中,加入了自抗擾控制算法,提高了電機的輸出穩定性能與抗干擾能力。
根據電磁耦合調速器的動力學特性,輸入轉速一定時,輸出轉矩與電樞和磁極之間的轉差存在非線性關系[19]。目的是為了找到對于電磁耦合調速器輸出轉矩最大的轉差速度,并通過LADRC算法進行轉差控制,在負載波動時保證了輸出轉速的穩定性,提高了電磁扭矩。
1 電磁耦合調速器模型
1.1 物理模型
電磁耦合調速器由電樞、磁極、電流控制器等部件組成,其原理是通過磁極繞組通入勵磁電流,與電樞之間建立磁拉力,磁極隨著電樞同方向轉動,傳遞動力。電磁耦合調速器結構示意圖見圖1。
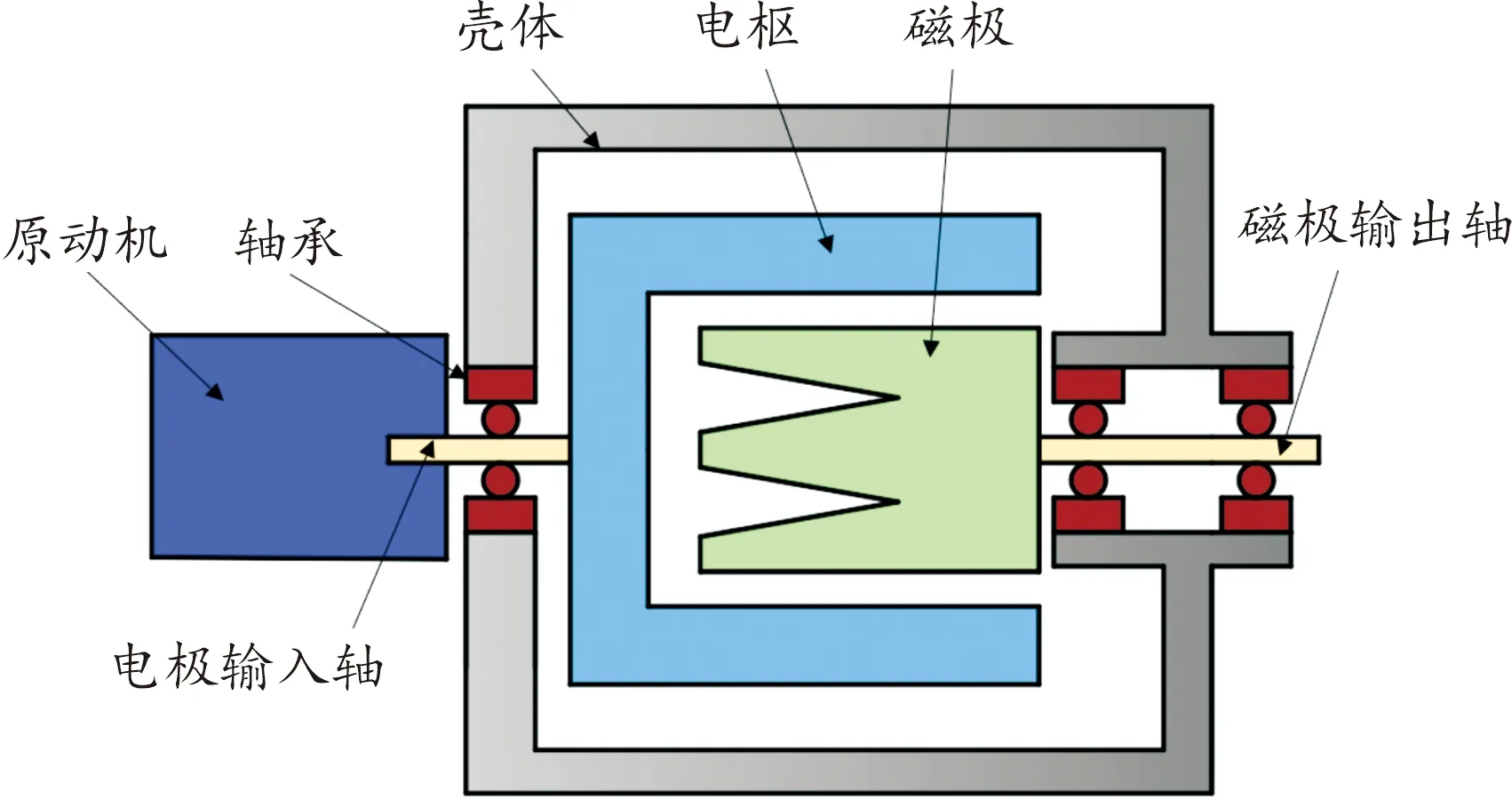
圖1 電磁耦合調速器結構示意圖
1.2 數學模型
電磁耦合調速器的基本模型如圖2所示。圖中,i為電流,u為電壓,θ為A相與d軸的夾角。
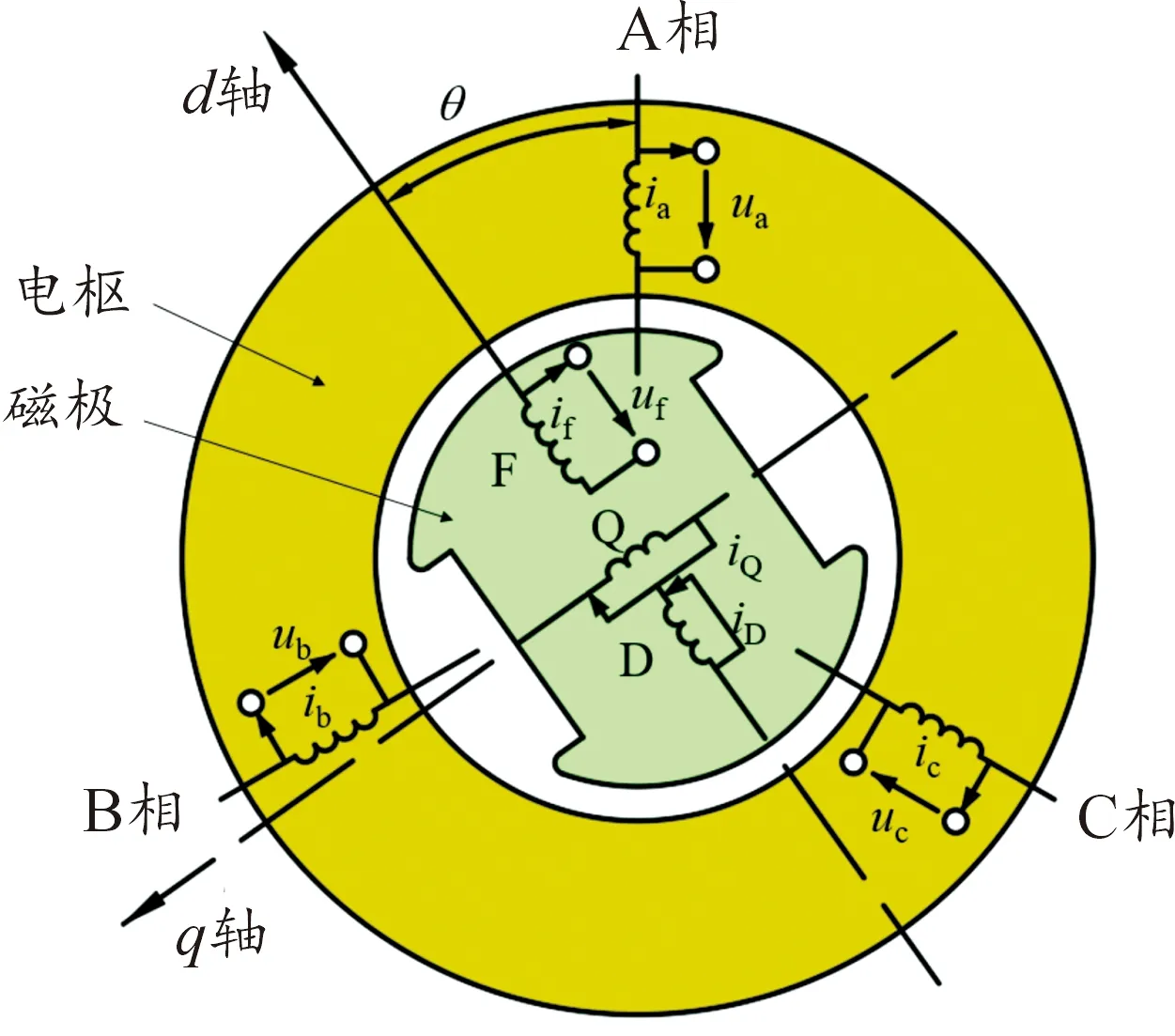
圖2 電磁耦合調速器基本模型示意圖
在建立電磁耦合調速器數學模型之前,需要對其做幾個假設,處于理想情況下易于建立其磁鏈方程、電壓方程、電磁轉矩方程與運動方程。假設如下:
1) 沒有磁路磁滯、飽和、渦流等現象。
2) 合成磁場間沒有相互作用力。
3) 電樞與磁極的磁場在換相過程中沒有電樞反應。
4) 沒有空間諧波、勵磁線圈漏磁等現象。
在推導電磁耦合調速器各方程之前,需要對電磁耦合部分進行電磁解耦[4],將電樞與磁極的各相電感、電流、電壓逐個分析,通過在電機自然坐標系下建立電磁耦合調速器的三相坐標,運用電機坐標變換理論(Clark-Park變換)進行線性變換,在旋轉坐標系(Odq坐標系)下表示。各坐標系關系見圖3。
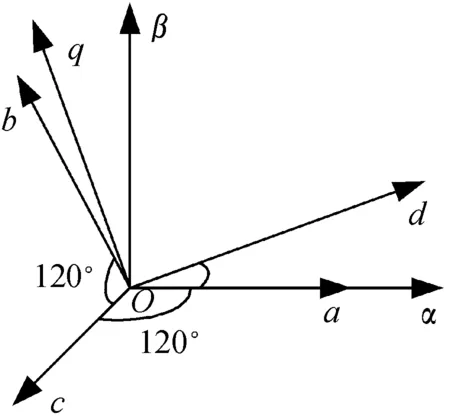
圖3 各坐標系的關系示意圖
在圖3中,Oαβ坐標軸為靜止坐標系,Oabc為電機自然坐標系,Odq為旋轉坐標系。通過電磁解耦推導電磁耦合調速器的數學模型。
1.2.1磁鏈方程
根據電磁感應定律,電磁耦合調速器的磁鏈方程為:
(1)
(2)
(3)
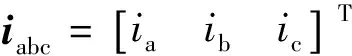
(4)
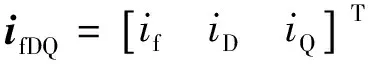
(5)
式中:L為電感系數矩陣;ψx為在x軸上的磁鏈(x= {a,b,c,f,D,Q});ix為在x軸上的電流(x={a,b,c,f,D,Q})。
由于繞組在旋轉坐標軸之間不存在相對運動,繞組通過電流產生的磁通恒定,阻尼繞組之間正交等因素,根據文獻[4]中的整理方法可得:
(6)
式中:Ld、Lq、Lo分別為d、q、o軸上的電感;Lf為勵磁繞組的自感;LD、LQ為阻尼繞組的自感;mof、moD、moQ分別為電樞三相繞組與磁極勵磁繞組、阻尼繞組D、阻尼繞組Q的互感振蕩幅值。
1.2.2電壓方程
電磁耦合調速器繞組示意圖見圖4。
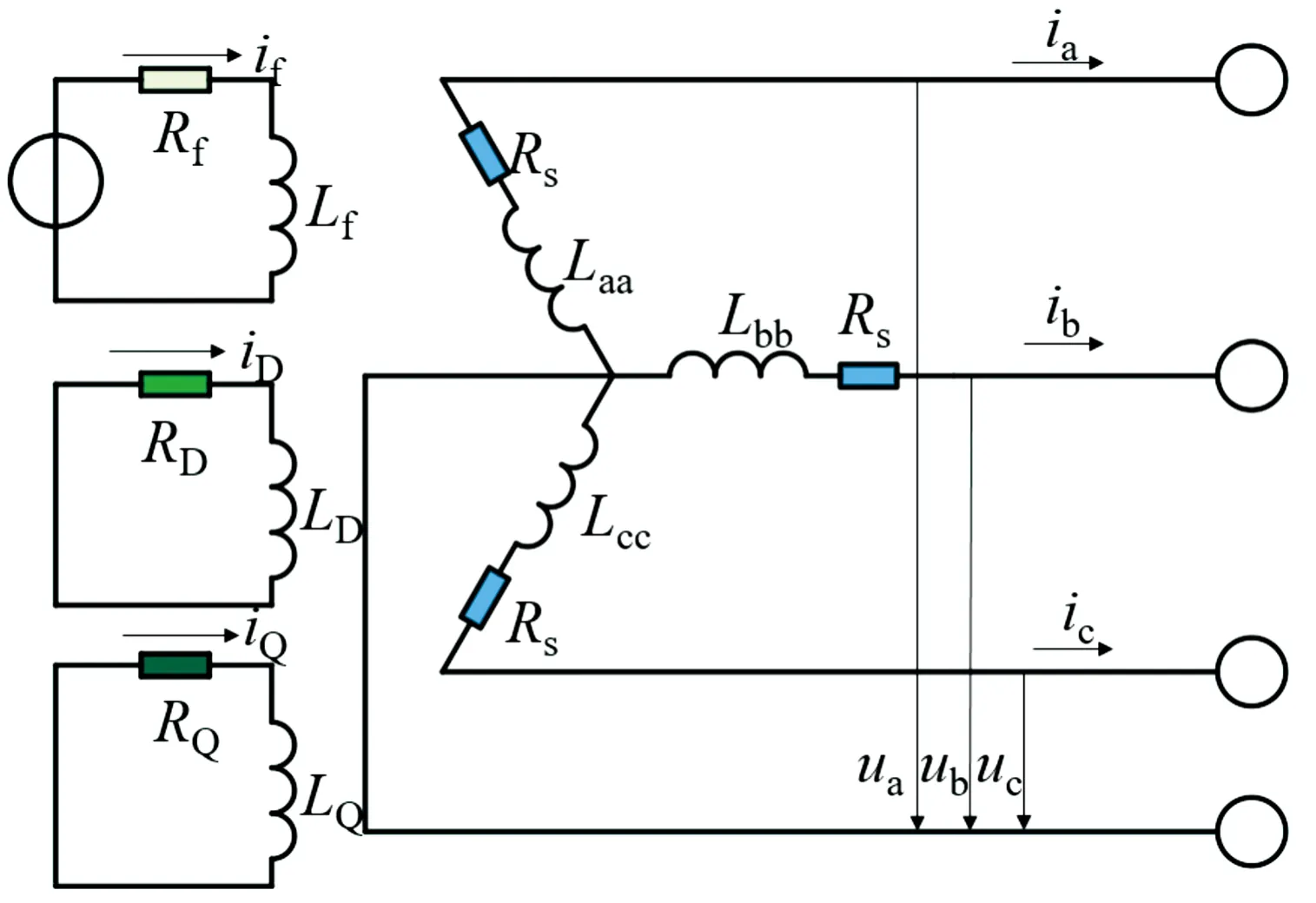
圖4 電磁耦合調速器繞組示意圖
根據基爾霍夫電壓定律求得各繞組的電壓方程:
(7)
(8)
(9)
Ro=RsE
(10)
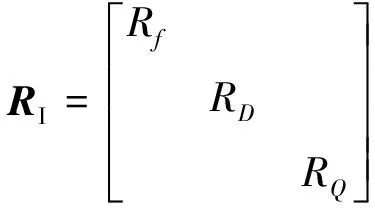
(11)
式中:ua、ub、uc分別為電樞a、b、c繞組相電壓;uf為勵磁繞組的勵磁電壓;Rs為三相繞組的電阻;Rf為勵磁繞組的電阻;RD、RQ為對應阻尼繞組的電阻;E為三階單位矩陣。將式(6)代入電壓方程整理可得:
(12)
式中:ΔΩ為電樞與磁極之間的相對轉速。
根據式(6)與(12)可得d軸與q軸的等效電路,見圖5和圖6。

圖5 d軸等效電路

圖6 q軸等效電路
1.2.3電磁轉矩方程
根據機電能量轉換原理[20],電磁耦合調速器的轉矩方程為:
(13)
整理后在Odq坐標系下表示為:
(14)
1.2.4運動方程
電磁耦合調速器輸入與輸出無直接的機械接觸,其具有與原動機相連的電樞和與輸出連接的磁極,對于其運動方程,需要單獨建立。運動方程參數詳情見表1。
電樞:
(15)
磁極:
(16)

表1 運動方程參數詳情
2 電磁耦合調速器仿真模型
2.1 Simulink仿真模型
對電磁耦合調速器數學模型中的磁鏈方程、電壓方程、電磁轉矩方程與運動方程進行整理可得:
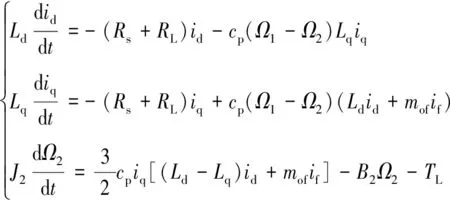
(17)
利用Matlab/Simulink進行仿真模型搭建,見圖7,其各參數見表2。
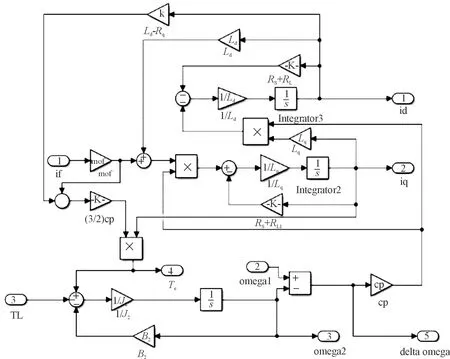
圖7 電磁耦合調速器的仿真模型示意圖

表2 電磁耦合調速器仿真模型參數
2.2 動力學特性分析
針對電磁耦合調速器,進行其動力學特性分析。將勵磁電流if、輸入轉速Ω1與負載扭矩TL作為仿真模型的輸入量,通過其數學模型得到d、q兩軸的電流id與iq,輸出轉速Ω2,電樞與磁極之間的電磁轉矩Te,與轉差ΔΩ。
當勵磁電流與負載轉矩為恒定時,改變輸入轉速影響轉差,得到其轉差與電磁轉矩之間的曲線關系。此為電磁耦合調速器的動力學特性曲線,見圖8(if=10 A)。
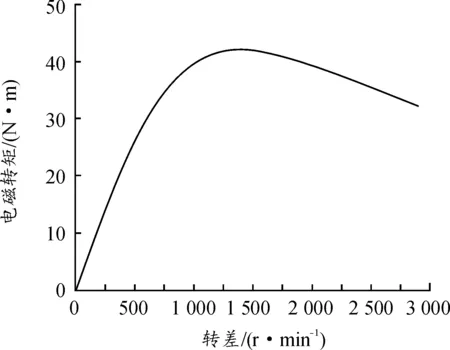
圖8 動力學特性仿真曲線
根據其動力學特性仿真曲線分析可得,當勵磁電流一定時,電樞與磁極之間的輸出扭矩受轉差的影響,當轉差在1 400 r/min附近時,電樞與磁極之間的動力傳遞效果明顯。根據損失功率計算公式
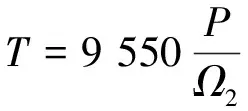
(18)
分析可得,輸入轉速為定值,當控制轉差一定時,輸出轉速n也為定值,傳遞扭矩T越大,則輸出功率P越大。針對目標轉差在1 400 r/min時,設計控制器并對其轉差進行控制。提高電樞與磁極之間的扭矩傳遞性能。
3 轉差自抗擾調節器設計
采用一階LADRC,其機構簡單,線性控制方便。基本控制模型見圖9。
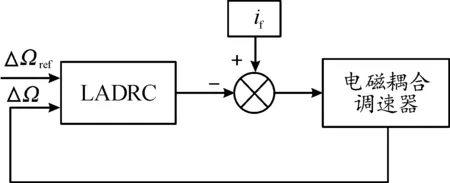
圖9 電磁耦合調速器轉差基本控制模型示意圖
設定目標轉差ΔΩref,通過LADRC控制器判斷誤差,調節勵磁電流的值,實現控制轉差的目的。
LADRC控制模型由比例微分器(tracking differentiator,TD),線性擴張狀態觀測器(liner extended state observer,LESO)與線性誤差反饋(liner state error feedback,LSEF)組成。圖10為一階自抗擾模型。
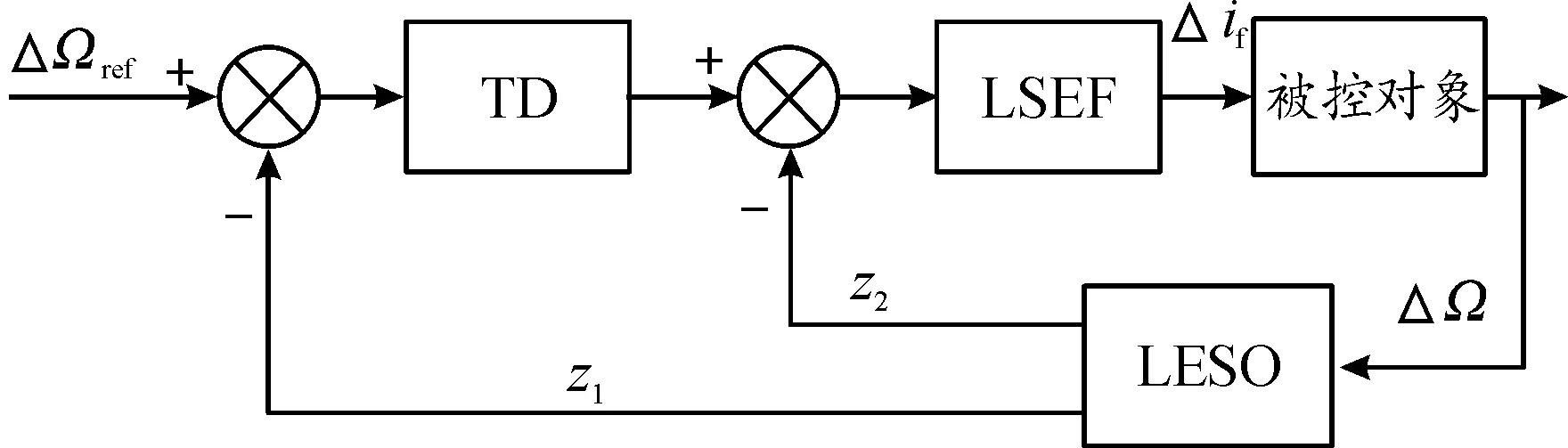
圖10 LADRC控制模型示意圖
在設定目標轉差ΔΩref后,TD可迅速跟蹤目標信號,將控制模型中的轉差迅速接近ΔΩref。將當前誤差傳遞給LESO進行誤差放大,LESO再將信號傳遞給LSEF,通過誤差反饋修正,輸出勵磁電流控制量Δif,調節轉速差,使其迅速消除誤差,達到ΔΩref。
3.1 TD設計
TD的設計目的在于迅速跟蹤目標轉差信號ΔΩref,可利用PID算法思想中的比例環節,通過設定誤差的比例迅速跟蹤目標值蹤,設定比例為kp。
3.2 LESO設計
LESO的設計目的在于將當前轉差輸出值與當前勵磁電流控制量之間的狀態觀測,將自身擾動與外界擾動相互抵消的策略,再將當前狀態變量反饋給TD與LSEF進行進一步的自抗擾調節。LESO的設計核心為控制狀態方程的設計。在圖10中的LESO可設計為:
(19)
(20)
對上式整理可得:
(21)
3.3 LSEF設計
LSEF的設計目的在于將TD與LESO輸出的反饋信號做誤差調節,輸出正確的反饋率,設計為常數調節,在仿真測試中進行測試。
4 自抗擾控制仿真
4.1 控制仿真模型
LADRC的仿真模型見圖11,控制參數設置見表3。電磁耦合調速器轉差控制仿真模型見圖12,仿真參數見表4。
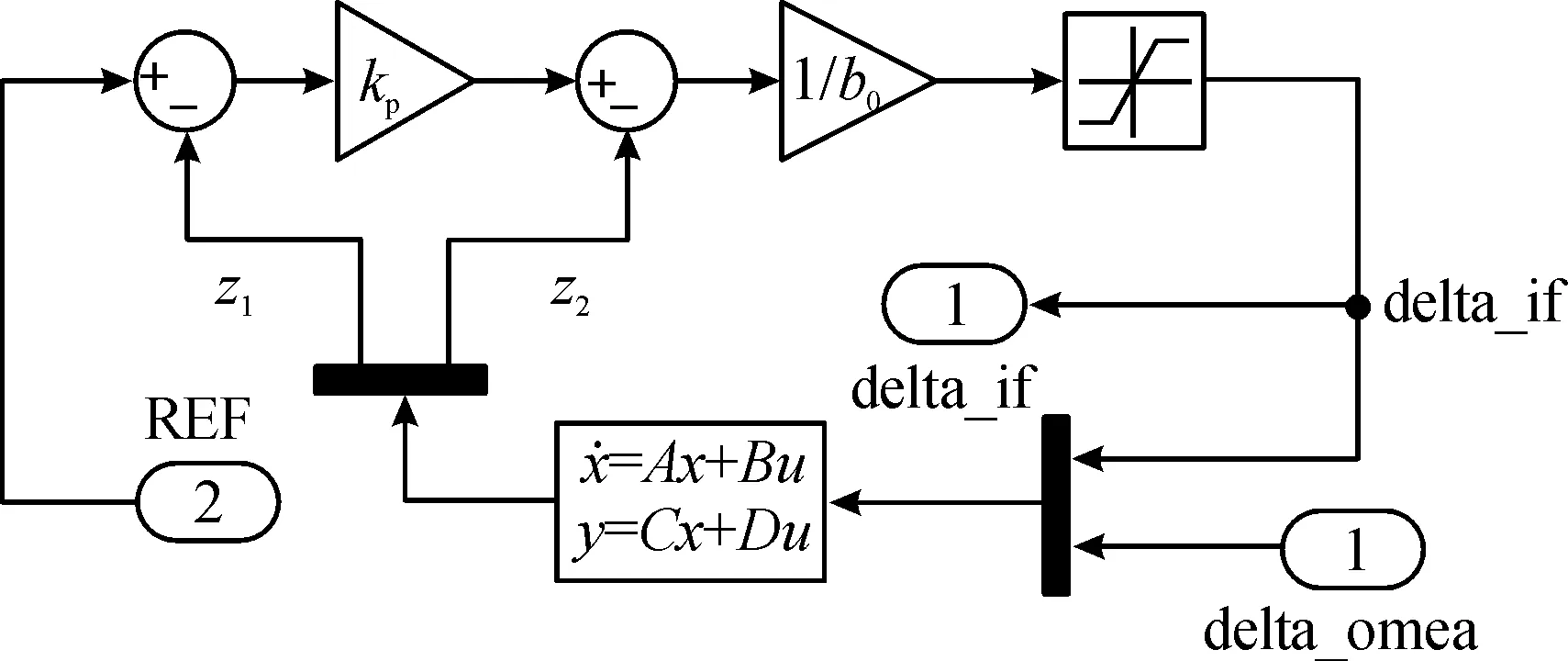
圖11 LADRC仿真模型示意圖

表3 仿真參數
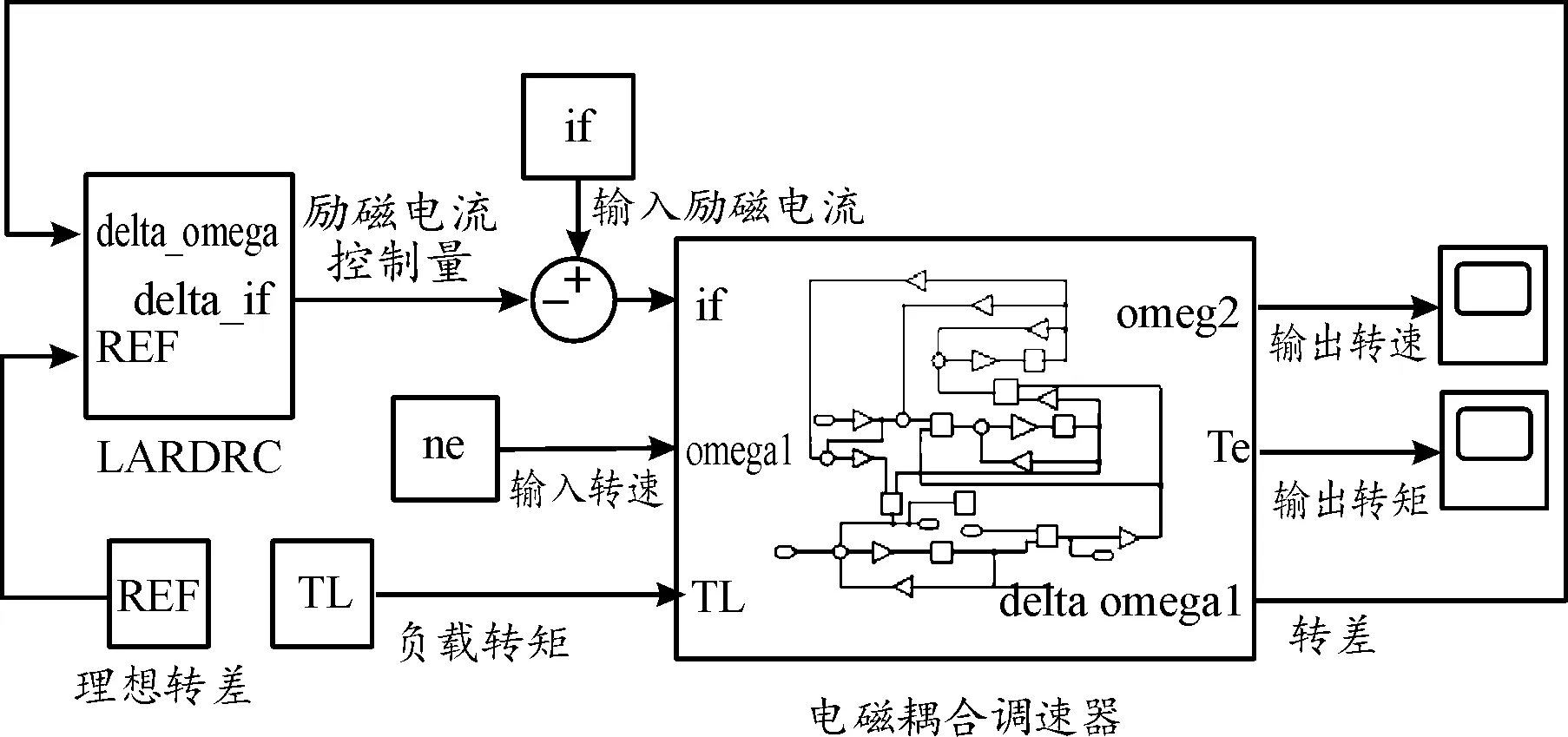
圖12 電磁耦合調速器轉差控制仿真模型示意圖

表4 電磁耦合調速器輸入仿真參數
4.2 仿真控制效果
為了方便觀測仿真效果,將LADRC與PID控制相比較,轉差仿真效果見圖13。其數值分析見表5。在相同勵磁電流下,以不用控制算法的電磁耦合調速器模型為對照組,電磁轉矩仿真曲線見圖14,當前轉差仿真曲線見圖15。具體數值分析見表6。
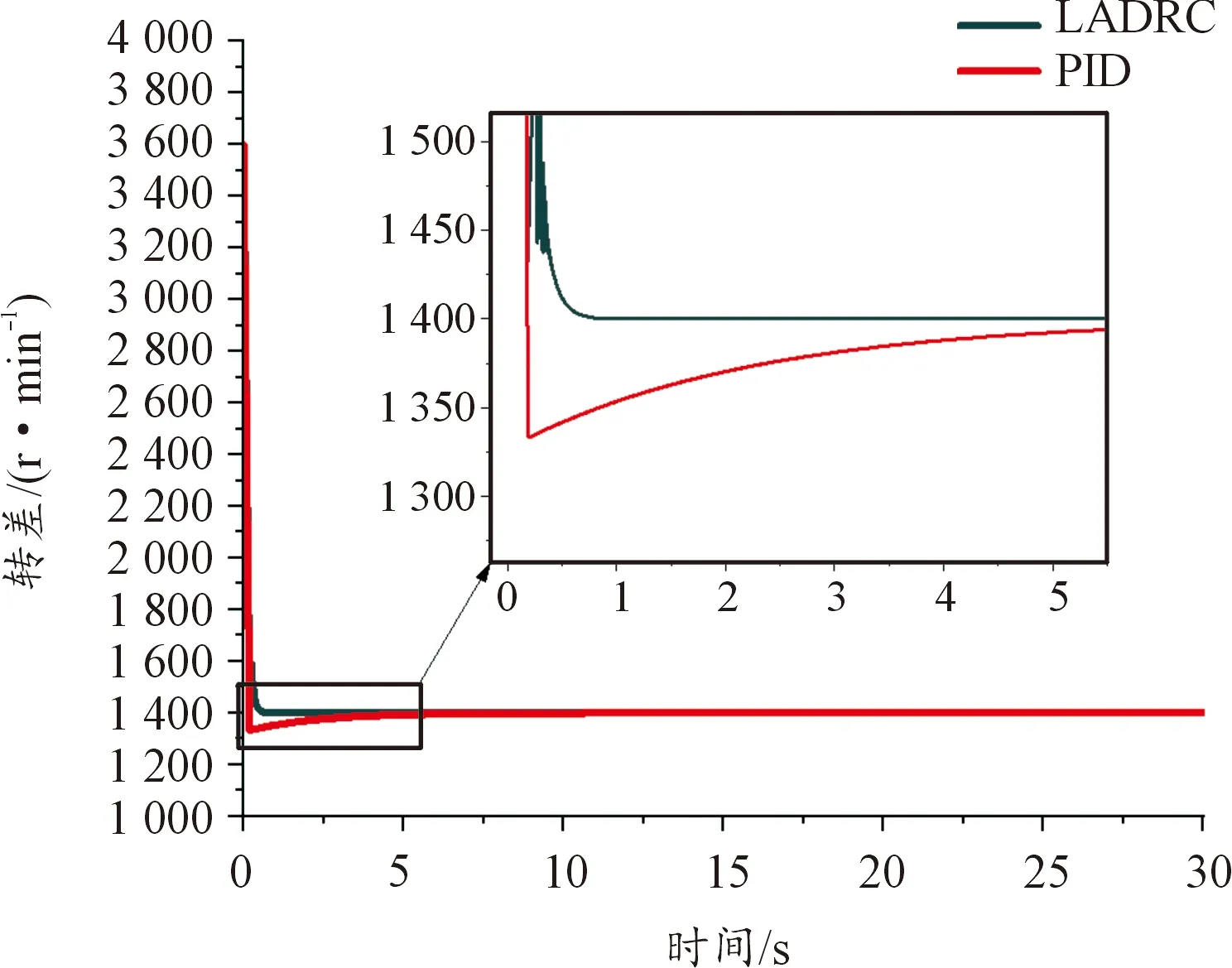
圖13 電磁耦合調速器轉差仿真曲線

表5 轉差仿真曲線數值分析
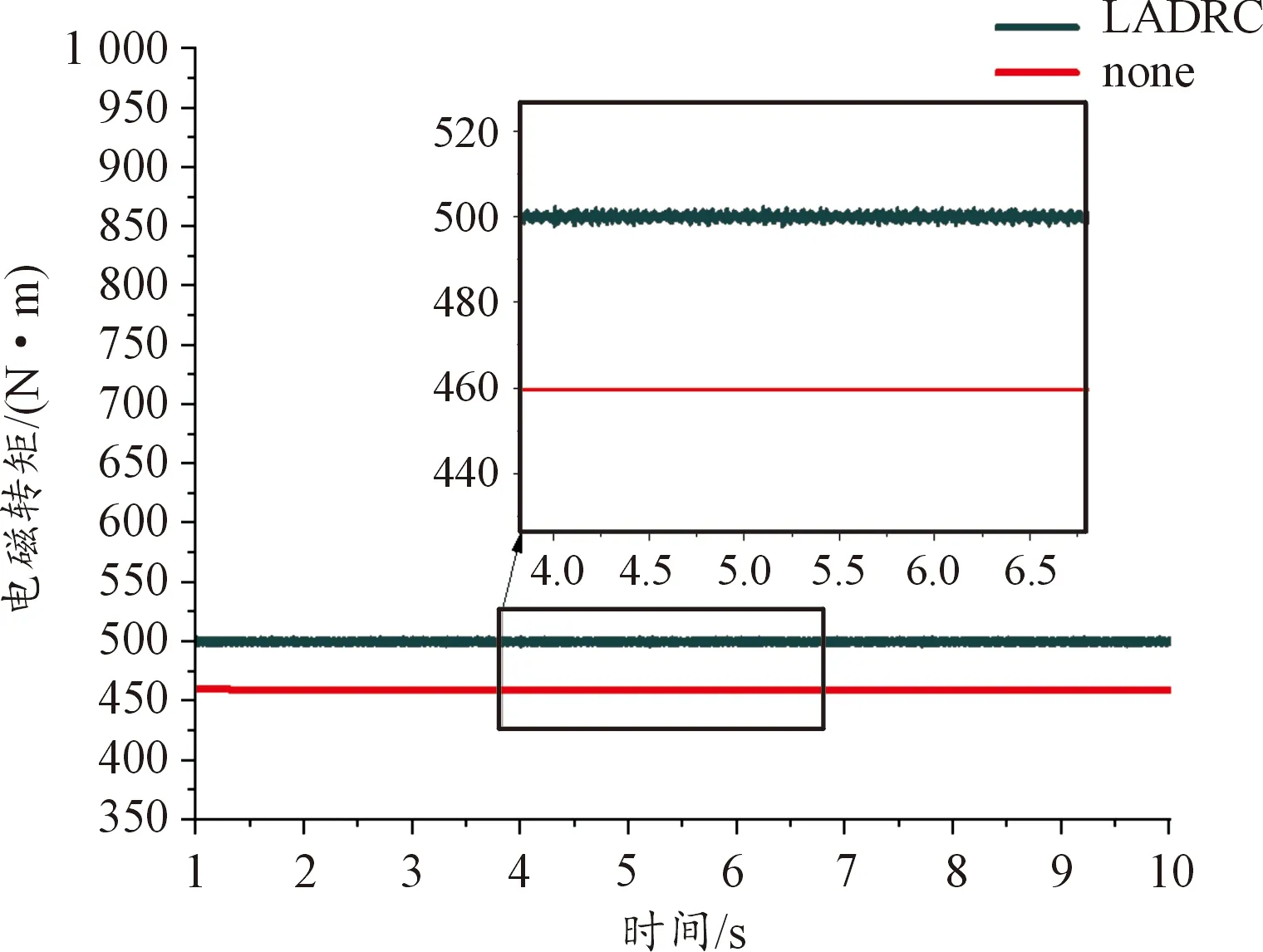
圖14 電磁轉矩仿真曲線
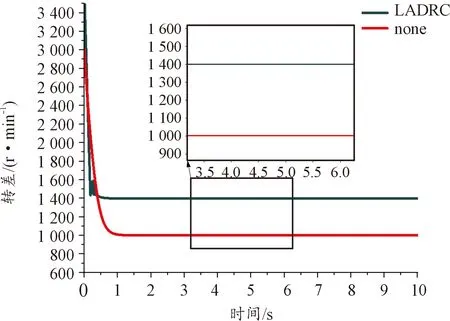
圖15 轉差仿真曲線

表6 具體數值分析
為了測驗自抗擾能力的魯棒性,在LADRC與PID同時穩定時,仿真時間第20 s加入20%的電磁扭矩擾動,觀測其曲線變化,具體見圖16,數值分析見表7。
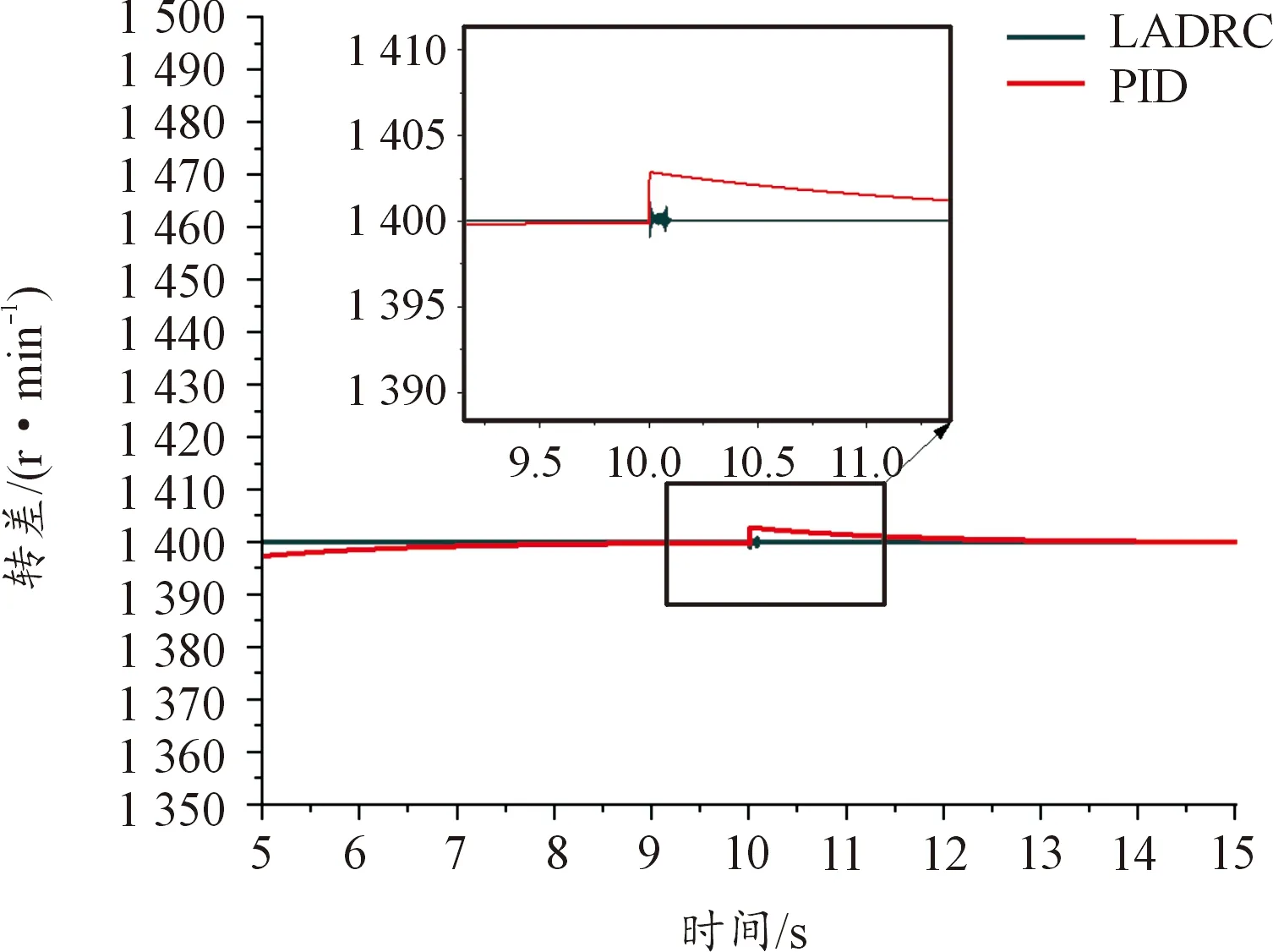
圖16 抗擾動能力仿真曲線

表7 轉差仿真曲線數值分析
嘗試在變負載情況下觀測自抗擾的穩定性,在LADRC與PID同時控制穩定后,輸入負載扭矩用隨機噪聲輸出,具體見圖17,效果圖見圖18。輸出轉速見圖19。
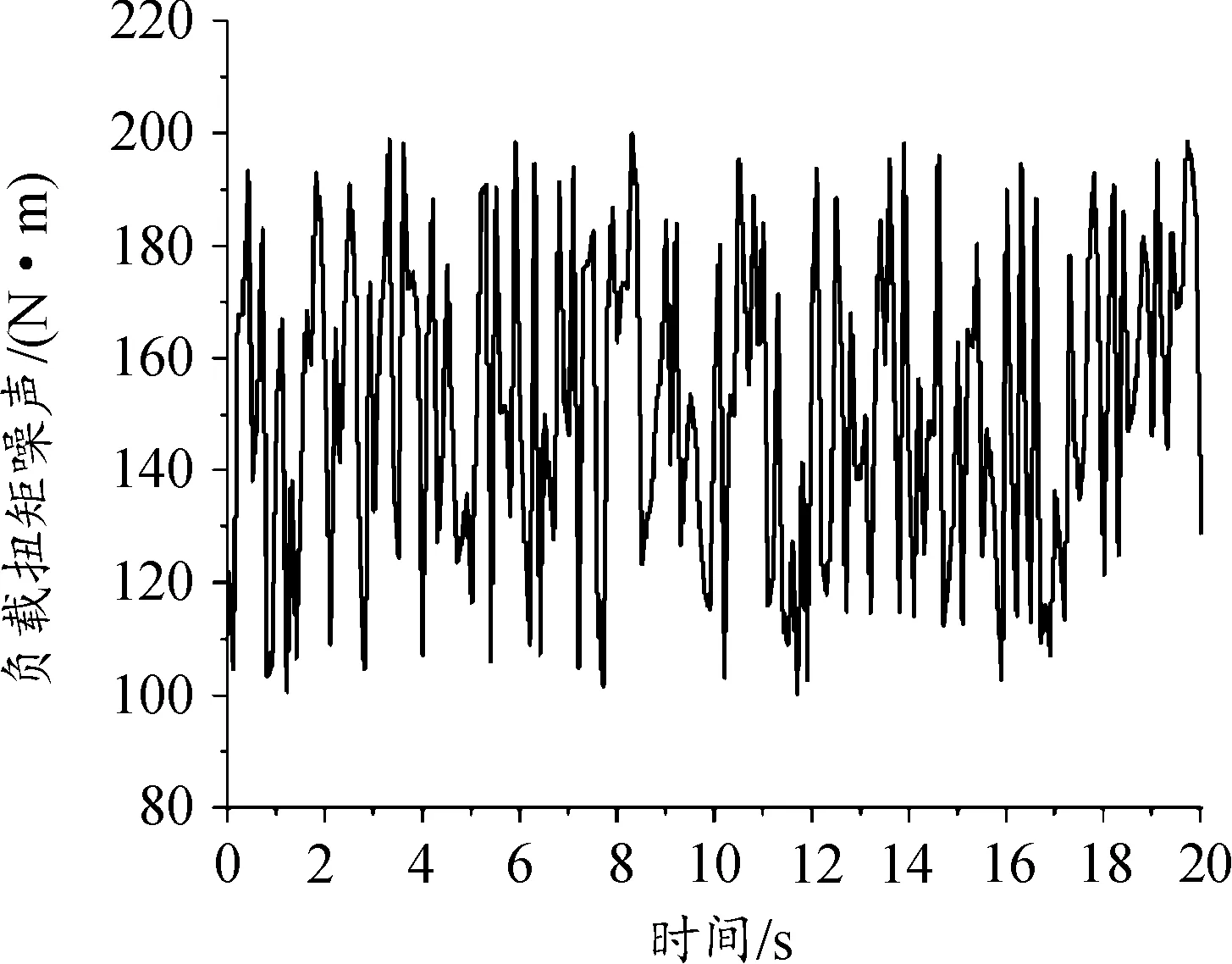
圖17 負載扭矩噪聲
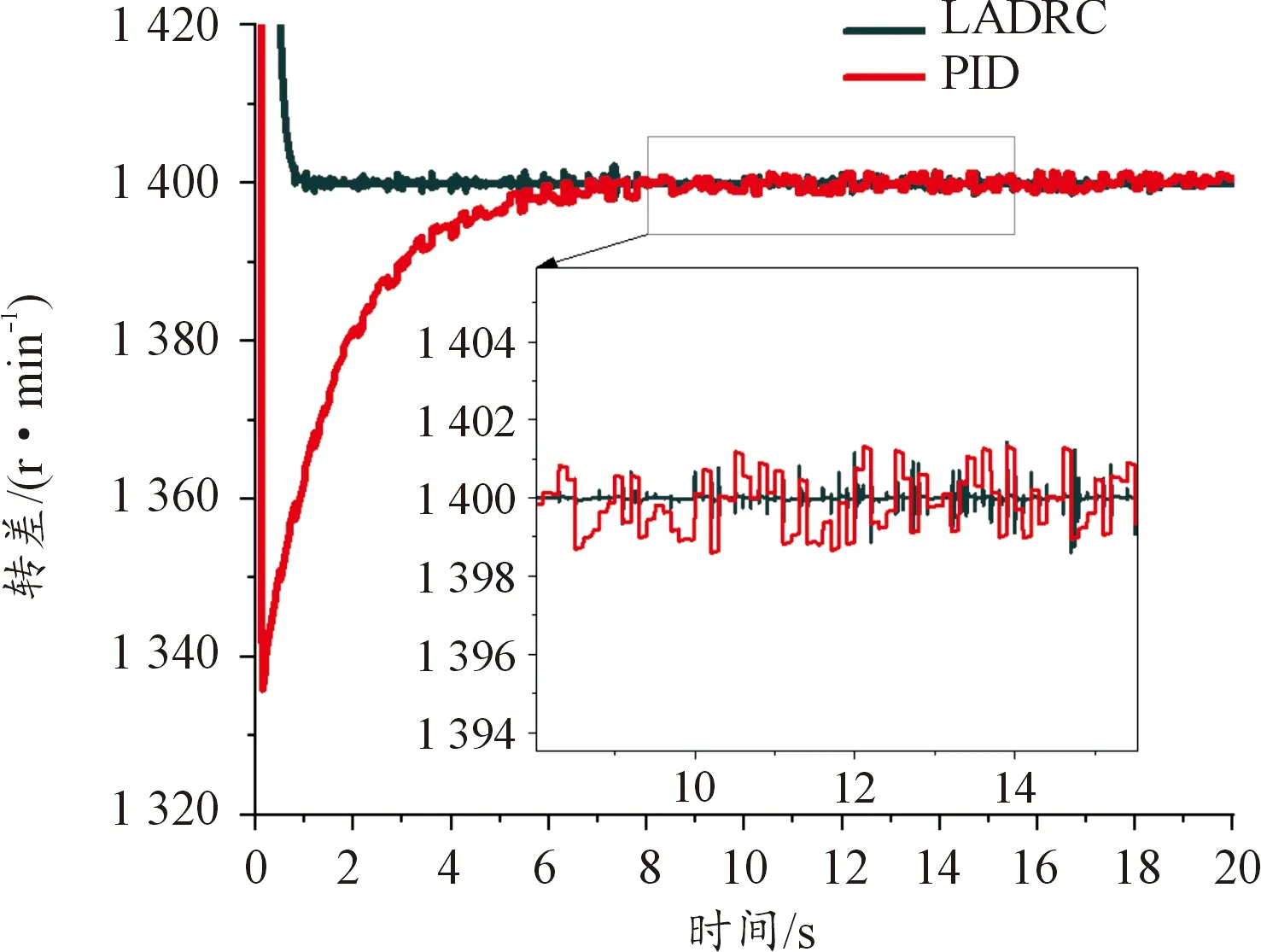
圖18 抗噪聲擾動能力仿真曲線
4.3 仿真控制效果分析
根據圖13、表5分析可得,LADRC的轉差控制效果要優于PID控制,能夠避免超調,大幅縮短穩定時間。根據圖14、圖15與表6分析可知,控制合理的轉差能夠有效地提高電磁扭矩的大小。根據圖16、圖18、圖19與表7分析可知,LADRC較于PID具有更好的魯棒性,在外界干擾下,能夠利用LESO的特性,將外界擾動與自身擾動相互抵消,提高了控制器的穩定性,在負載波動時保證了輸出轉速的穩定性。
5 結論
1) 仿真結果表明,電磁耦合的電樞與磁極之間的轉差與電磁轉矩存在非線性關系,當原動機輸入轉速一定時,合理控制其轉差能夠提高二者之間的電磁轉矩。
2) LADRC較于傳統PID控制具有更好的效果,提高了電磁耦合調速器轉差控制的響應速度與穩定性,在負載波動時保證了輸出轉速的穩定性,提高了電磁耦合調速器的轉速輸出性能。

