非等溫平行流下吹吸式通風系統流場的數值模擬

王 寅，趙福云, ，唐宇飛，文雅冰

（1. 武漢大學 動力與機械學院，湖北 武漢 430072；2. 湖南工業大學 土木工程學院，湖南 株洲 412007）

0 引言

21 世紀來，隨著“中國制造2025”與德國“工業4.0”[1]概念的提出，我國工業建筑數量不斷增加，而工業場所會排放出各種污染物，包括有毒有害氣態污染物和顆粒物等。因此工業建筑室內環境問題也引發研究者的關注，如何有效控制污染物擴散成為學者研究重點[2-3]。吹吸式通風系統作為常用的局部通風方式，主要結合吹吸氣流實現污染處理目標，是一種高效通風方式，對室內污染物清除有很大優勢。

目前有關室內有障礙物吹吸式通風的討論較多，在理論與模擬方面，孫一堅[4]對氣流罩合成理論進行分析，得出了不同參數設置下吹吸氣流特性。于航等[5]通過微積分進行分析，確定吹吸氣流動量變化情況，所得結果對明確吹吸氣流流場特性有重要意義。林愛暉[6]應用CFD（computational fluid dynamics）模擬了卸料斗中氣相及氣固兩相流場，總結含塵氣流流動特性，指出雙側吹吸通風能有效控制粉塵擴散。馬駿馳[7]研究了非等溫條件下吹吸式通風系統中流場和污染物的分布規律。實驗研究中，付海明等[8]建立了縮比例模型，分析模擬煙霧發生器污染氣流對粉塵等顆粒污染物的影響，通過調整風量、模型尺寸討論吹吸氣流對流場結構影響的最佳參數。Ojima J.等[9]在吹吸式通風系統流場內設置了人體模型，分析得出捕集效率不會發生顯著變化。Zhou Y.等[10]研究發現人體對該系統吸收污染物影響較小。對比文獻[9-10]和美國政府工業衛生家協會（ACGIH）的實驗可知，對該系統吸收污染物影響顯著的是風口尺寸。同時障礙物后形成的渦流區與污染物擴散有較大影響。R. T. Hughes[11]發現障礙物在射流區域2/3 后，相應影響明顯降低，通風系統清除性能也受到影響。

上述研究表明，在內有障礙物的吹吸式系統中，送風射流特性對流場有著顯著影響。本文擬基于非等溫射流情形下，分析吹吸式通風系統內存在障礙物的流場以及清除污染物性能的情況，以期為吹吸式通風系統優化設計提供參考。

1 數值計算模型

1.1 物理模型

本文模型為一個簡化的三維單體房間，參照文獻[12]建立物理模型，如圖1 所示。

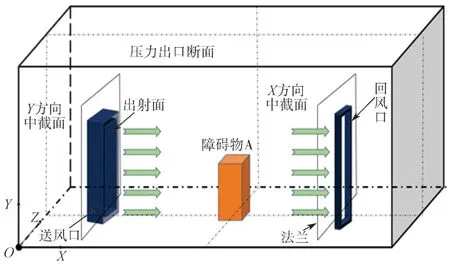
圖1 三維吹吸式通風系統示意圖Fig.1 Schematic diagram of the three-dimensional blow-suction ventilation system

實驗室尺寸為長5.64 m、寬14.01 m、高3.27 m。按照通風系統數值模擬方式，通風系統設置在離墻面（Y=0）3 m 處，為進行補風，在距離通風系統5.64 m 處的外墻上設置單獨一個窗口，尺寸為0.75 m×1 m。整個房間門窗全部保持關閉狀態。在模擬時由于小窗補風氣流比較微弱，故簡化處理時忽略其影響。設置坐標原點為頂點的O點。吹風口、排風口上下均設置了擋板，其寬度為2.0 m、長度為1.5 m，吹風口尺寸和排風口尺寸均為0.50 m×0.96 m×0.96 m。吹排風口間距3.8 m。吹排風口沿X軸間距3.8 m。同時，在吹排風口軸線中心的位置有一障礙物A，模型尺寸為0.64 m×0.64 m×0.64 m。

1.2 數學模型

吹吸式通風氣流流場為三維湍流場，基于三大守恒方程確定控制方程。研究過程中，為更好地滿足量化分析要求，需對流體進行如下計算分析：

RNGk–ε模型的湍流動能k和耗散率ε的方程為

式（4）～（5）中：v為運動黏度系數；vt為湍流動力擴散系數；σk和σε為湍流普朗特數；Pk和Gb分別為由慣性風作用和熱浮升力引起的湍流動能源項；C1ε、C2ε、C3ε為經驗常數，其中，C1ε=1.42，C2ε=1.68，C3ε=1.0。

用阿基米德數Ar[13]衡量溫度差對流體的影響，其計算公式如下：

式中：g為重力加速度，m/s2；do為當量直徑，m；Ts為射流出口溫度，K；Te為環境空氣溫度，K；u1為射流出口速度，m/s。

1.3 計算域與網格劃分

計算域整體尺寸為0.64 m×7.00 m×3.27 m，送風口出射斷面設為入口速度邊界（inlet），出風口設置為出口邊界（outlet），與Y軸垂直的兩個面設置為壓力邊界其余面邊界，設置為無滑移固體壁面邊界且設為定壁溫。考慮模擬對顆粒軌跡的計算將受湍流的隨機性影響，本模擬設置的顆粒性質為MgCO3，粒徑為1.5×10-5m，顆粒受湍流的影響較小。運動速度和入口風速一致。對于網格劃分，將三維吹吸式通風系統劃分為規則四邊形網格，而排風口周邊形狀不規則。選擇單元網格Tex/Hybird，運用此類型網格對整個計算區域進行劃分，分別為40 萬、50 萬、60萬和70 萬。為了驗證網格無關性，檢驗其獨立性，在非等溫工況下對比吹吸式流場軸心速度曲線，軸心速度在不同網格數下的變化趨勢如圖2 所示。

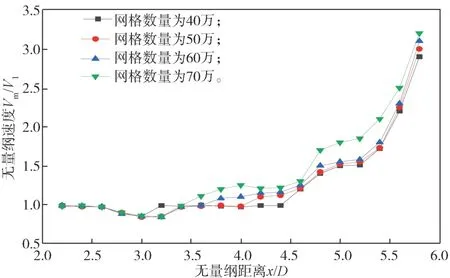
圖2 各網格數下的無量綱速度分布圖Fig. 2 Non-dimensional velocity distribution diagram for each grid number

由圖2 的對比結果可知，40 萬、50 萬、60 萬網格的無量綱速度趨勢基本一樣，而70 萬偏差較大，考慮計算準確可靠性和計算時間成本，將網格數量設置為60 萬最佳。

2 模型驗證

為了驗證非等溫工況下本通風系統數值模擬的準確性和可靠性，將RNGk-ε湍流模型的模擬計算結果與文獻[14]的實驗結果進行比較，其比較具體的測點分布如圖3 所示。

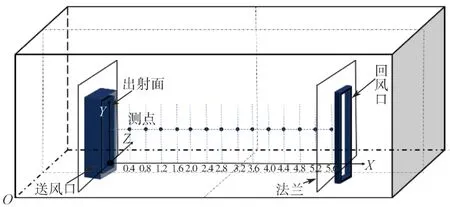
圖3 實驗測點分布圖Fig. 3 Distribution map of experimental points

實驗室規模大小為11.3 m×7.1 m×3.3 m，吹風口尺寸為0.5 m×0.5 m，風口與墻體間隔1 m。軸心測點沿著X軸方向，設置測點間隔0.4 m，測量軸心流速；Z軸上設置監測點，用于測量X截面上系統運行的最大速度。實驗通過送風口控制送風溫度為305.76 K，與室內空氣溫度293 K 形成溫差。在吹風口前端布置3 kW 的電熱絲加熱升溫，實際溫度可達32.6 ℃，阿基米德數為0.024。實驗工況具體參數如表1 所示。

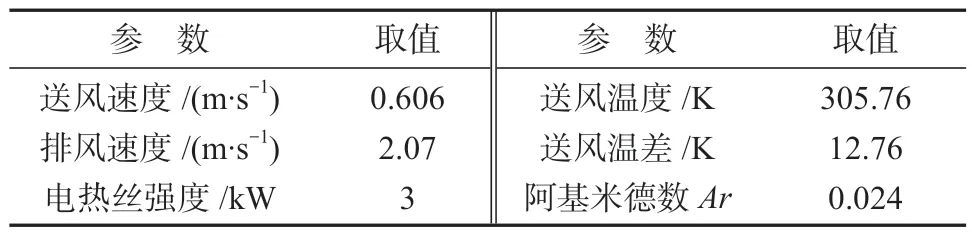
表1 實驗工況參數表Table 1 Test condition parameter table

將模擬結果與實驗數值進行擬合，結果如圖4 所示。A1為送風口尺寸，V為測點速度，V1為送風口速度，V2為排風口速度，Vmax為X截面上顯示的最大速度，H為最大速度所對應的高度，x為橫坐標，D為入風口到回風口距離，Tm為軸心溫度，To為室內環境溫度，T1為風口射流溫度，無量綱溫度。顯然，數值模擬結果與實驗結果變化趨勢基本吻合，故本文采用的數值模型在非等溫工況氣流流動的模擬計算是可行的。

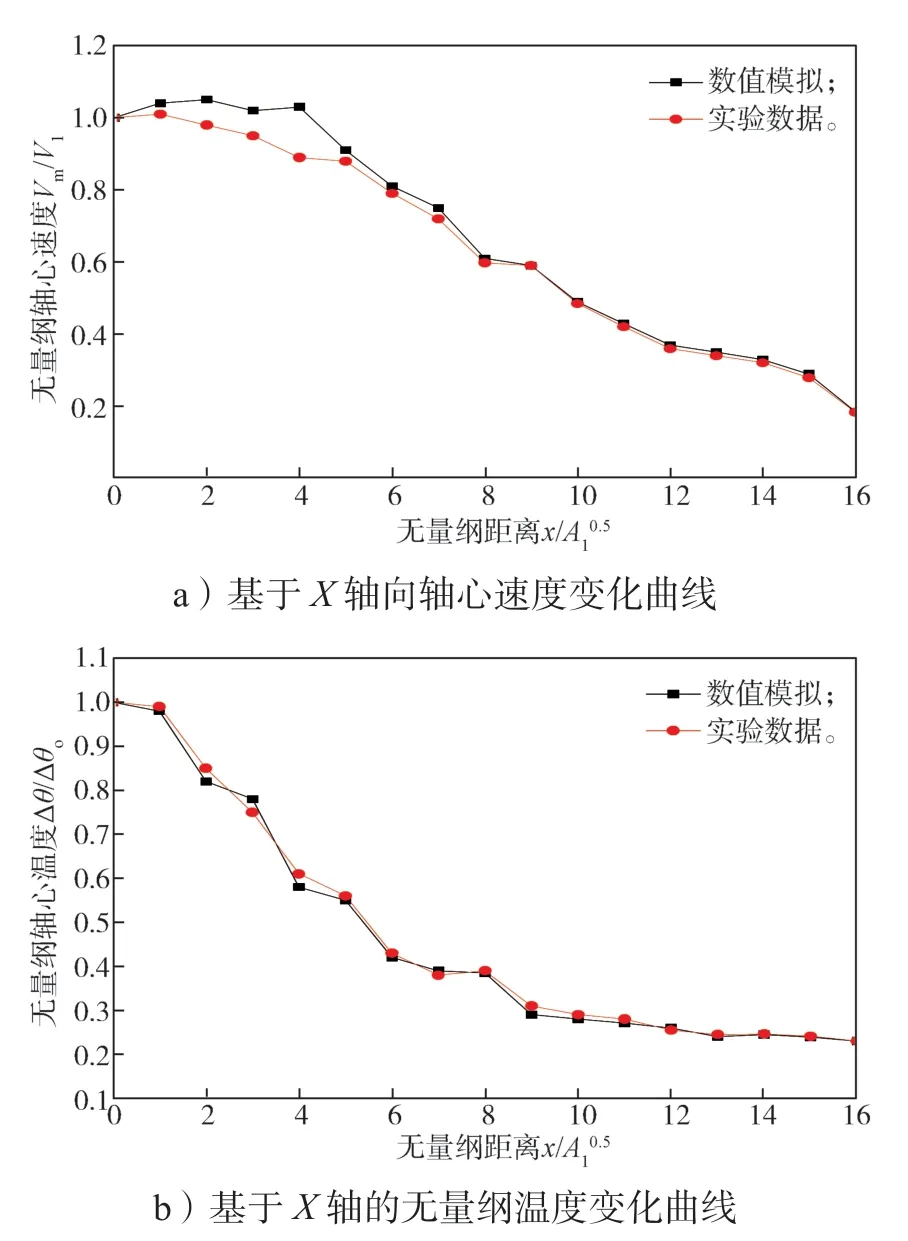
圖4 數值模擬與實驗結果對比Fig. 4 Comparison between numerical simulation and experimental results

3 結果與討論

本文分析了吹吸式通風流場的基本特性，討論兩方面（一是不同送風溫度，二是不同送風速度）條件下，對流場的軸心速度、溫度分布、示蹤粒子捕獲效率以及渦流中心高度變化的基本規律。

3.1 不同送風溫度下的吹吸式通風流場特性

3.1.1 送風溫差工況設置

本文參考了文獻[14]實驗設置條件，設置送風速度為0.606 m/s，排風速度為2.07 m/s，以保持模擬與實驗條件的一致性。而環境溫度設置為293 K,軸心速度為Vm，送風溫差采取等梯度（3 K）設置，分別設置為0, 3, -3, 6, -6, 9, -9, 12, -12, 15, 18 K 等11種工況，具體工況參數設置如表2 所示。

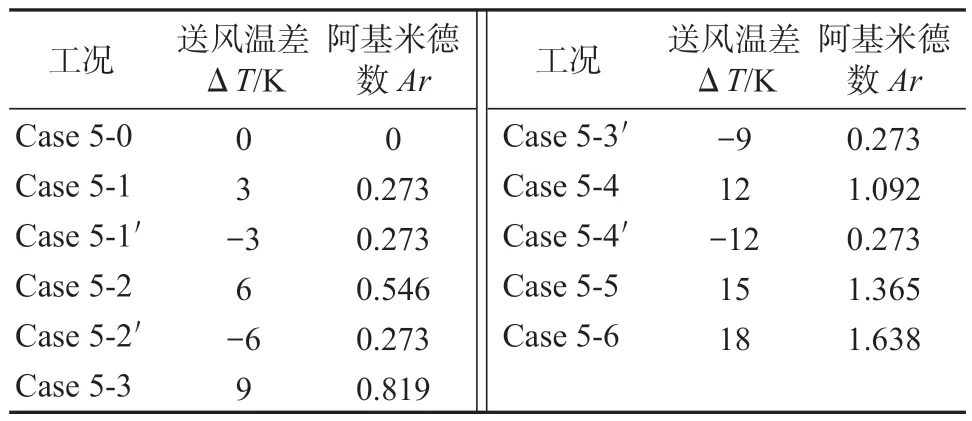
表2 變送風溫差工況表Table 2 Working condition table of variable supply air temperature differences

3.1.2 軸心速度變化規律

由前面模型驗證結果可知，在障礙物條件下，Case 5-0 軸心速度沿X方向是逐步遞減的。當送風口之間間隔4.7 m，由于匯流場的影響，軸心速度加快。當射流溫度高于室內環境溫度時，從圖5 可以發現，在送風溫差在6 K 內，障礙物前側速度變化放緩。然而當送風溫差大于6 K 時，軸心速度緩緩增加，之后下降。當靠近排風口時，速度會先增大后減小，之后速度急劇增大至接近排風速度。在上升期，隨著送風溫度增大，軸心速度也增大。

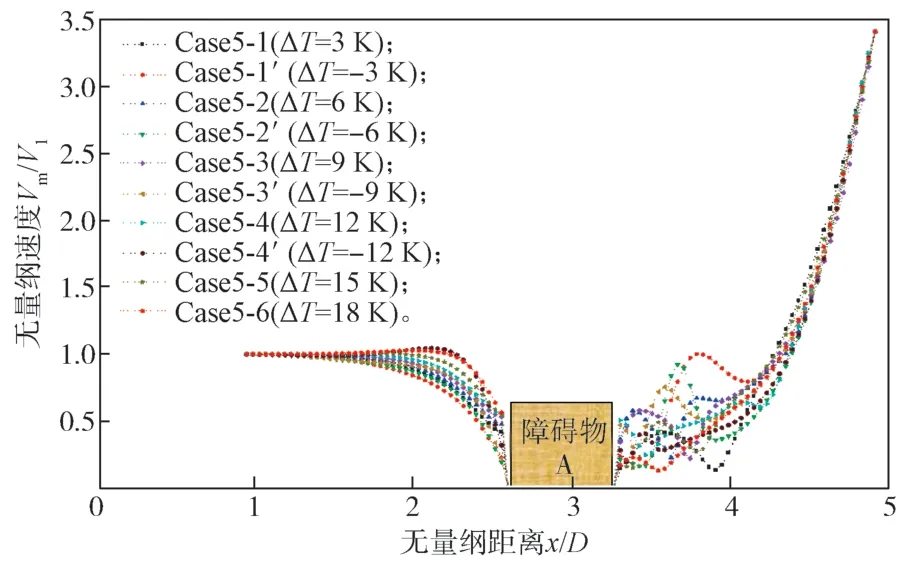
圖5 各送風溫差下的軸心速度-距離變化曲線Fig. 5 Axial velocity distance change curves with a temperature difference of variable air supply

3.1.3 軸心溫度變化規律

本文為了更清晰反映變化趨勢，將軸心溫度無量綱化，在多種送風溫度下，軸心溫度變化曲線見圖6。

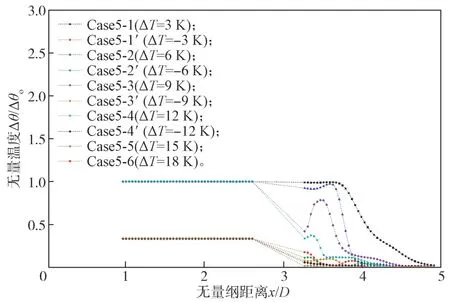
圖6 各送風溫差下的無量綱軸心溫度-距離變化曲線Fig. 6 Non-dimensional axis temperature distance change curves under variable air supply temperature differences

從圖6 中可看出，送風溫度增大情形下，軸心無量綱溫度會加快遞減。當溫差為3 K 時，無量綱溫度在x/D=3.67 處開始遞減，當溫差達9 K 時，在x/D=3.47 處開始遞減；溫差增大到18 K 時，其衰減點提前到x/D=3.2。遞減起點實質上和送風口的距離同時減小，軸心溫度沿著吹吸流場方向加快下降。

3.1.4 回流區渦流中心高度變化規律

為了研究回流區渦流中心向上偏移程度隨送風溫度的變化情形，對污染物累積的程度進行分析，主要討論Y=3.5 m 截面上的流體分離，渦流中心不同溫差條件下的偏移高度如圖7 所示。可以看出，在吹吸式流場內，當送風溫度增大，渦流中心偏移高度呈現類似周期性的先增大再減小，雖然渦流中心不斷升高，但基本維持1.1 m 左右。

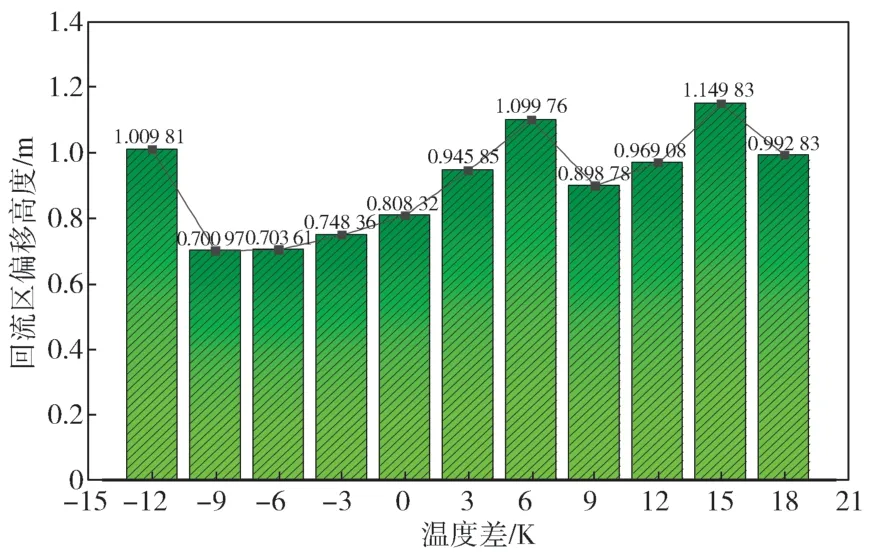
圖7 各溫度差下的回流區渦流中心偏移高度Fig. 7 Vortex center offset height in the recirculation zone under different temperature differences

3.1.5 捕集效率

本文在進行模擬時，假設對應的顆粒物為示蹤粒子，這種粒子的跟隨性高，計算分析并確定出排風口粒子數及比值，并計算出捕集效率η。

定義捕集效率η的表達式如下：

式中：m為排風口捕獲到的粒子數；n為吹風口釋放的粒子數。

即在吹風口加入的示蹤粒子，在不斷流動過程中，其中一部分進入排氣罩，有的則逃逸，然后模擬分析確定出排出的粒子數與釋放的粒子數之比，就可實現計算效率的目的。

引入示蹤粒子捕集效率這一指標，對比送風溫差擴大對示蹤粒子實際進入排風罩所占比例。如圖8所示，在非等溫射流情形下，送風溫差改變對示蹤粒子捕集效率有著顯著影響。在工況5-0（ΔT=0 K）下，示蹤粒子捕集效率達91.07%。溫差增大到3 K時，捕集效率增大到95.09%，當送風溫差繼續增大，捕集效率反而降低。隨著溫差繼續加大，捕集效率持續降低。這是由于送風溫度增大，阿基米德數Ar增大，熱浮升力加強，射流整體向上偏移。而過高的溫度導致偏移過大，流體不能被排風口流場引導，引起示蹤粒子逃逸。然而，當降溫送風時，阿基米德數Ar減小，氣流匯聚在障礙物之前，從而減小示蹤粒子的捕集效率。因此，適當調整送風溫度或者與環境溫度趨于一致時，污染物的捕集效率會較高，降低污染物逃逸能力。

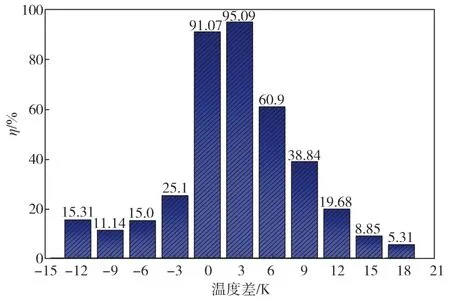
圖8 不同送風溫差下的示蹤粒子捕集效率Fig. 8 Tracing efficiency of tracer particles under different supply air temperature differences

3.2 不同送風速度下的吹吸式通風流場特性

3.2.1 送風速度工況設置

在升溫送風狀態下阿基米德數對污染物捕集效率影響顯著。在上述討論中，保持送風溫差為9 K，排風速度V2為2.07 m/s 時，污染物捕集效率僅為38.84%，具有較大余量可供優化分析。送風速度采用等梯度（0.3 m/s）設置，改變送風速度V1，設置6種等區間工況進行模擬。環境溫度保持To=293 K，不同送風速度工況如表3 所示。

表3 各送風速度下的工況Table 3 Working conditions under variable air supply speeds

3.2.2 軸心速度變化規律

圖9 為各送風速度之下軸心速度變化曲線。如圖9 所示，射流速度的改變對軸心速度影響顯著，對于工況6-0（V1=0.606 m/s）來說，風速較低，流體受熱浮升力與慣性力雙重影響，隨著距離x增大，軸心速度先增大后減小。當增大送風起始速度，降低熱浮升力與慣性力比例，隨著距離增大，軸心速度下降緩慢。隨著送風速度繼續增大，在射流范圍內軸心速度下降得更加顯著，也就是說送風速度增大，射流控制的區域范圍將會增加。當達到障礙物之后，距離的增大軸心速度受排風口射流速度的影響更加顯著。

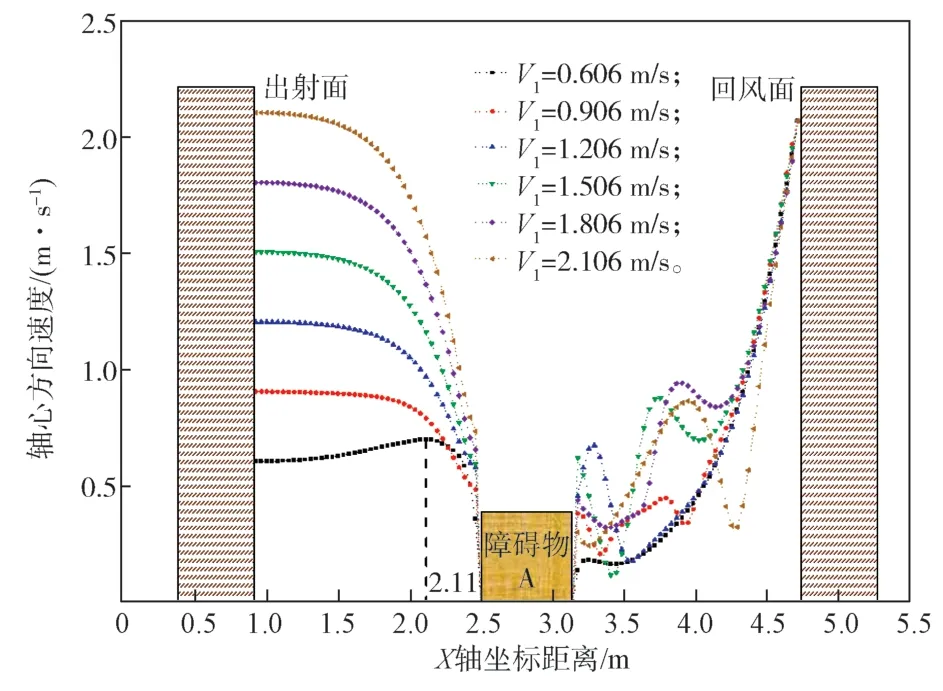
圖9 各送風速度下的軸心速度變化曲線Fig. 9 Axis speed change curves under variable air supply speeds

3.2.3 軸心溫度變化規律

圖10 為各初速度下軸心溫度變化曲線。從圖10的變化曲線中可以看出，在送風速度較低時，空氣受熱浮升力的影響較大，障礙物A 后的空氣受擾動較小，軸心溫度更接近環境空氣溫度。隨著送風速度增大，風壓產生的慣性力隨之增強，軸心溫度出現先增后減的情形，且速度越大，溫度衰減的起點越延后。然而，當送風速度增大到1.806 m/s 時，溫度衰減點為x/D=3.9。隨著風速繼續增大，溫度衰減緩慢，這是因為速度增大，Ar反而減小，在慣性力的主導作用下，氣流維持水平流動。

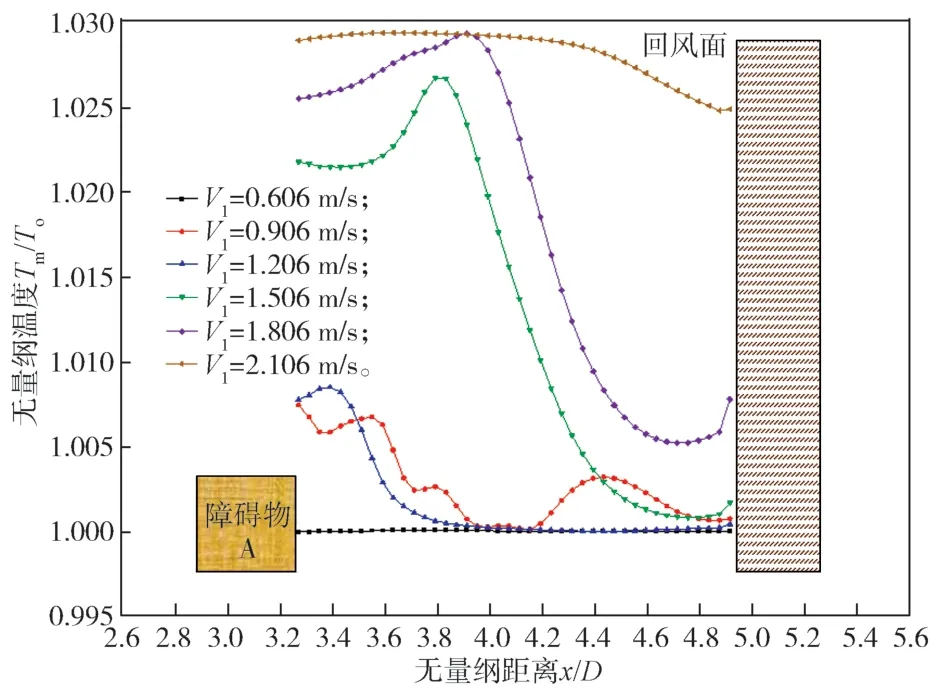
圖10 各初始速度下的軸心溫度變化曲線Fig. 10 Axle temperature change curves under each initial speed

3.2.4 回流區渦流中心高度變化規律

圖11 為各送風速度下回流區渦流中心偏移高度模擬結果。

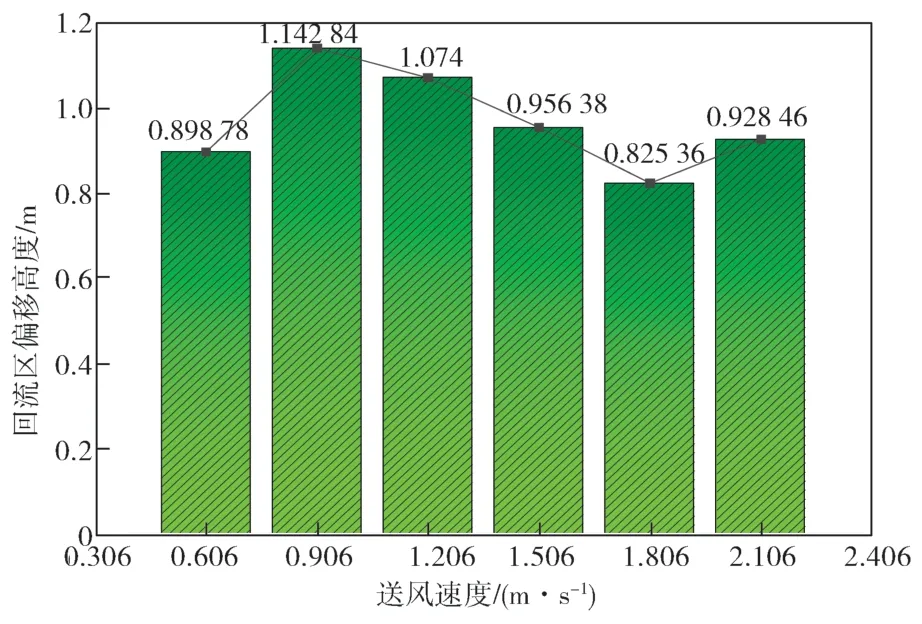
圖11 各送風速度下的回流區渦流中心偏移高度Fig.11 Vortex center offset height analysis in the recirculation zone under various air supply speeds

由圖11 的結果可知，在吹吸式通風流場內，隨著送風速度增大，回流區渦流中心渦流偏移高度呈現先增大后減小的趨勢，向上偏移程度下降。由于送風速度增大即阿基米德數減小，渦流中心不斷升高，然而基本維持在1.1 m 以下的范圍。然而，送風速度越大，Ar數遞減，熱浮升力與慣性力的比值下降，即慣性力占主導地位。送風射流沿著平行軸線的方向流動，從而控制整個流場。

3.2.5 捕集效率

為了直觀地反映出吹吸流場基于不同風速條件下對捕集效率帶來的影響，將初始速度不同的工況進行比較，如圖12 所示。

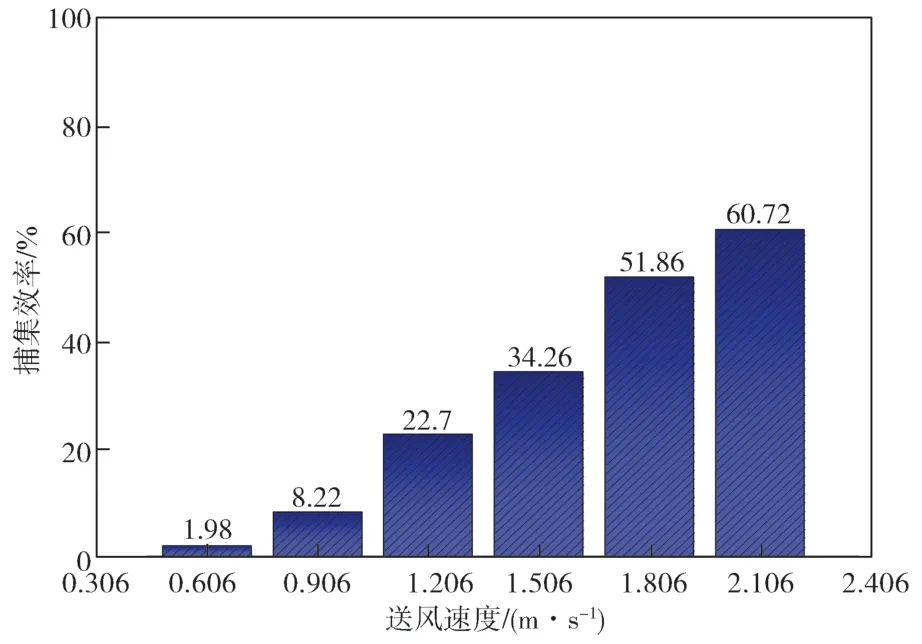
圖12 各送風速度下吹吸流場針對污染物捕集效率產生的影響分析Fig. 12 Analysis of the influence of the blow-suction flow field on the pollutant capture efficiency under variable air supply speeds

從圖12 中可以看出，對非等溫吹吸式通風系統而言，送風速度的改變顯著影響示蹤粒子實際的吸收性能。捕集效率隨著送風速度的增大而增大。當送風速度增大到1.806 m/s，捕集效率增大到51.86%。這是由于送風速度增大，阿基米德數Ar變小，即熱浮升力相較于慣性力減弱，空氣也漸漸地與軸線平行，送風射流能夠將示蹤粒子送到排風速度口中。故捕集效率隨著送風增大， 即合理地增大風速來增大污染物的捕集效率是可行的。

4 結論

本文主要針對非等溫射流條件下吹吸式通風系統流場規律進行了討論，基于送風溫差和送風速度，從軸心速度、溫度分布、渦流結構以及示蹤粒子的擴散等變化進行分析，主要有如下結論：1）采用RNGk-ε湍流模型模擬非等溫射流條件下吹吸式通風系統流場，模擬結果與實驗數據對比結果表明，兩者的趨勢基本一致，吻合較好。2）當射流與環境空氣存在溫差時，隨著溫差擴大，阿基米德數增大，軸心速度快速遞減；軸心溫度沿著吹吸流場方向加快下降。渦流中心偏移高度呈現出先增大后減小的趨勢。而對于污染物擴散方面，當送風溫差達6 K 時，即阿基米德數大于0.546，整個系統的捕集效率也顯著降低；當送風溫度接近環境溫度時，整個系統的捕集效率較大，吹吸式系統吸收污染物的能力最強。3）當射流與環境空氣溫度一定時，擴大射流速度，即阿基米德數減小，射流沿著流場軸心運動，軸心溫度先增大后減小，同時射流影響的區域范圍將會增加，有利于提高捕集效率。射流形成的渦流中心向上偏移程度下降。對污染物清除而言，合理地增加送風速度對于吹吸式系統的污染物清除是有利的。