基于風電場功率預測的數據價值研究

趙 越， 徐博涵， 王 聰， 高 鋒， 宋 潔

（1.北京大學 工學院，北京 100871；2.首都經濟貿易大學 統計學院，北京 100070；3.北京大學 光華管理學院，北京 100871）

1 引言

在國際上對節能減排日益重視的形勢下，風力發電作為一種新能源發電技術，因其資源豐富、污染小等特點備受矚目［1］。為了促進風電產業持續健康發展，國家能源局于2016年11月印發了《風電發展“十三五”規劃》，在規劃中提到，隨著世界各國對能源安全問題日益重視，加快發展風電已成為國際社會推動能源轉型發展、應對全球氣候變化的普遍共識和一致行動。

電力系統數據量龐大，是數據分析與應用的重要場景。風電相關數據常以時間序列的形式存在，通常將風速或風電的歷史數據與地理位置、氣象數據、機組參數整合分析。在風能資源評估場景中，有研究基于不同時刻風速數據，通過數值模擬降低保真度較低數據帶來的影響［2，3］，分析南海風能資源時空分布特征。在機組參數優化場景中，研究通過影響因子法篩選對參數影響較大的模態［4］，確定參數優選范圍。在風電預測場景中，研究使用K-means、DBSCAN等聚類方法檢測異常值、清洗數據［5］。上述研究都剔除了數據離群值，減少異常值對模型效果的影響，得到了顯著成效。由此看來，數據質量（價值）的提升是在應用中所需要的，針對數據價值的研究對模型效果的提升有著重要意義。但上述工作沒有把數據價值估算作為一種常態化機制，未從數據點的貢獻角度審視數據，存在遺漏重要數據點的可能性。并且海量數據中存在大量數據質量較低的部分，評估數據價值，根據數據重要程度高效選取數據有助于提高計算效率與預測精度。

為研究風電系統中數據價值，利用數據實現更精準的分析，本文以風電功率預測這一場景為例。考慮到電力的實時供需平衡和避免浪費等要求，預判能源的供應成為了必不可少的環節，準確預測風電功率能夠保證電網各個方面安全平穩的運行，改善風電企業的經濟效益。由于風電系統受風速、地形、氣壓、風機運行狀況等諸多不確定因素的影響，風電功率通常呈現非平穩性和隨機性［6］。現有的時間序列、機器學習，深度學習方法還無法實現對風力發電預測的精準預測。例如，Nfaoui等［7］利用ARMA對實際風電場出力預測的平均誤差為21.5%。丁志勇等［8］通過聚類和SVM模型進行預測，預測精度為83.96%。Zang等［9］利用遺傳算法優化長短期記憶網絡（LSTM）參數，準確率最高為87%。

電力系統數據資源極為豐富，蘊含著巨大的商業價值和支持科學決策的信息［10，11］，對數據價值的評估也尤為重要。數據交易與數據資產流通機制的建立，為綜合利用多方數據進行更為細粒度的預測提供了便捷條件［12］。然而，數據較于傳統要素具有非排他、非競爭等特性，導致目前數據價值評估尚沒有形成統一范式［13］。目前經濟學中的數據價值評估方法主要有成本法、市場法、收入法［14］。成本法通常低估數據價值［15］；而數據市場建設尚不完善為市場法評估帶來了困難，一些學者通過設計數據交易市場框架，探索數據市場中的均衡價格對數據定價［16，17］，這一類方法多會忽視數據本身的信息屬性。

收入視角是數據價值評估的重要思路：即加總全部收益中數據資產貢獻的現金流。由于從實際場景中拆分數據的回報較為困難，眾多學者選擇從數據挖掘角度，拆分數據的作用。例如，在供應鏈場景下，評估有無數據對報童模型優化結果的影響，量化數據的貢獻［18，19］；在醫療場景中，利用貝葉斯框架計算數據為決策目標減少的不確定性，如完全信息價值（expectedvaluewithperfectinformation，EVPPI）等指標，據此平衡數據獲取的成本與收益輔助決策［20，21］。能源系統數據資源豐富，獲取成本低，更重要的是探索系統內哪些數據在任務中更加重要。沙普利值（Shapleyvalue）是由諾貝爾經濟學獎得主勞埃德·沙普利［22］提出，是合作博弈論中經典的收益分配方法，其滿足了現實收益分配場景中一系列公平性原則，被用于評估平臺為多個利益相關者分配數據價值的應用［23］。有些學者指出在機器學習模型中，沙普利值的計算需要指數級別的時間［24］。為了應對計算復雜度過大的挑戰，一些學者提出了近似計算沙普利值的算法，例如k-近鄰近似沙普利值、蒙特卡洛近似沙普利值［25，26］。在機器學習的基礎上，一些學者提出使用強化學習（DVRL）進行數據評估，使用數據值估計器（DVE）計算數據點在模型訓練中使用的可能性，與預測器模型一起自適應地學習數據值［27］。然而，數據價值研究多基于理論與算法設計，與實際場景結合較少，在風電預測領域尚缺乏與數據實際價值結合的有效預測方法。

現有電力預測研究對數據的價值挖掘較少，沒有通過數據對預測工作帶來的經濟效益進行量化研究。本文基于數據—預測—決策—收益的框架，將系統中的實際收益與模型預測精度掛鉤，從而對數據的貢獻——其價值有更準確的估計。具體而言，首先，本文構建了考慮多種數據的風電功率預測模型，然后使用沙普利值對發電功率預測場景下的數據價值進行評估。其次，本文將從特征與樣本點兩個維度分析風電歷史數據的價值，并根據高／低價值數據分析各自數據特點，為事前的數據價值提供參考。進一步，本文使用數值實驗分析去除和添加不同價值數據對模型的影響，提出一種基于價值函數計算數據價值的框架，作為一項啟發性研究，本文可以為電力系統中的數據收集與動態管理提供策略參考。

2 預測—價值評估模型設計

2.1 問題描述

風電場的經濟收益與調度計劃息息相關，調度計劃取決于對次日發電功率預測的準確率和誤差，影響當天電力市場的出清。因此，本文對日前功率預測與接下來的經濟收益建立模型，表1展示了本文使用的變量列表。具體地，設t∈｛0，1，…｝為日期，h∈｛0，1，2，…，23｝為小時，電力系統在t日h時的風力發電功率為Pt，h。電力系統在第t天預測t+1天各小時風力發電功率，設預測值為P＾t+1，h，h=0，1，…，23。假設需求相對穩定，若預測發電功率大于實際，即電力供給不足，需要通過額外調度風電和火力發電保證電量供給。設火電發電每千瓦成本為w，針對額外調度的情況設定懲罰系數k，則預測不足情況下總成本可表示為（1+k）w。若預測發電功率小于實際：該時刻風電處于過剩狀態，此時火力發電機組根據預測值進行了額外發電，其成本為w。假設風電場每單位供電能獲得的收益為r，本文給出風電場每日的收益為

表1 參數說明

2.2 風電功率預測

本文構建以長短時記憶網絡（LSTM）為主體的神經網絡預測短期風電輸出。該網絡由多個記憶存儲單元連接而成，其對時間序列數據的處理過程如（2）～（7）式所示。LSTM 的主存儲單元基于輸入的風電序列［Pt-7，h，Pt-3，h，Pt-2，h，Pt-1，h］、上一單元的隱藏層輸出Ht-1、輸入權重w，以及偏置b。通過輸入門it了解當前網絡狀態，通過遺忘門ft記憶序列的重要信息，最終利用輸出門oi更新單元中的信息，得到當天風電預測數據

在建立多輸入—多輸出模型時，選取LSTM 作為主體，在此基礎上將氣象數據與風電數據輸入不同的結構中進行處理，模型結構如圖1所示。首先將歷史風電功率（歷史3天數據與一周前數據）輸入LSTM 層，抽取時間序列數據特征，再將LSTM層的輸出與氣象數據一起輸入全連接層，經過計算輸出未來24小時的預測結果。

圖1 改進的LSTM模型

2.3 價值評估

沙普利值為了解決公平分配合作博弈得到的收益的理論［26］。沙普利值計算每位參與者的邊際收益均值決定各個參與者的合作貢獻

其中S為全集，n=｜S｜，i∈S，v是合作博弈的效用函數，代表合作的收益，φz（v）表示元素z在效用函數v定義下的貢獻，也就是元素z的沙普利值。在數據挖掘場景中，v一般為模型目標函數或準確率，φz（v）則為每個數據點對挖掘任務的貢獻。沙普利值具備完備、公平、可加性等特性，適合在數據—模型—價值鏈條中拆分各個數據或特征的貢獻。

針對風電場預測場景，電力系統的收益與預測誤差高度相關，本文選取Rt-R*t作為效用函數v，即

數據沙普利值的計算復雜度較高，并且算例中數據集規模較大，每一次計算“邊際效用”v（D）-v（D／｛i｝）都需重新訓練模型，精確計算需要消耗大量計算資源。因此，本文采取沙普利值近似算法：截斷蒙特卡洛沙普利值法（truncatedmonte carloShapley，TMC-Shapley）估計價值［24］。該算法利用隨機排序抽樣估算每個數據點的邊際貢獻，當部分數據集的效用函數接近完整模型時，就停止該序列的邊際貢獻計算，進入下一次序列循環，從而節約計算成本。

3 算例分析

本節使用2017—2018年風電場發電功率數據建立功率預測模型，并使用沙普利值方法分別評估該場景下的數據樣本與特征的價值，進一步利用數值實驗驗證本文所選取數據價值評估方法的合理性，然后結合電力系統實際提出一個數據管理框架，以改善數據使用效率。

3.1 數據概述

本文數據包括來自歐洲的哥白尼氣候數據庫（ERA5），為無線電探測的氣象現場數據，采樣間隔為12小時，以及2017年與2018年中國各省風電發電量數據，共17520個數據點，采樣間隔為1小時。風速等氣象數據是影響風力發電的主要因素，因此本文將星期、歷史氣象數據（氣壓、溫度、風向、風速、風速南北方向分量）、前3天和一周前的歷史發電功率，總計共103個特征作為模型輸入，未來24小時的風電功率作為模型輸出。為了防止不同量綱對預測精度的影響，本文對數據進行歸一化處理。按照8∶2的比例劃分訓練集和測試集。

3.2 預測精度與收益

為了評估所提模型性能，本文將該模型與普通的LSTM模型、隨機森林（RF）和極限梯度提升樹（XGB）進行比較。同時采用均方誤差（MSE）、平均絕對誤差（MAE）分析模型的誤差，采用相關系數（cor）、擬合優度（R2）分析模型的精確度。各評價指標的計算公式如下

其中M表示樣本數量，表示第t天h小時的預測值，Pt，h表示第t天h小時的真實值。本文對數據集中的10個省份進行預測。為保證模型結果的魯棒性，本文選取40個隨機種子進行重復實驗，比較各模型在所有數據集上的表現，計算每個模型評價指標的均值等統計量。如表2所示，本文提出的改進的LSTM模型擬合優度和相關系數最高，MSE和MAE最小，說明本文所構建的模型具有較好的預測效果和穩健性。

表2 各省模型預測效果

為證明結果具備統計意義的顯著性，對實驗結果進行弗里德曼（Friedman）檢驗。設立原假設為不同模型的效果無顯著差異，顯著性水平α=0.05，對四種模型和各項平均值進行檢驗，得到χ2值和p值，如表2最后兩列所示。對于每一個評價指標，四種模型呈現出顯著性（p＜0.01），因此拒絕原假設，意味著模型效果之間呈現統計意義上的差異，說明改進的LSTM模型結果在統計意義上是較優的。

所有省份中，遼寧、吉林、新疆、云南四個地區效果最好，其擬合優度、相關性都處于0.90以上，預測誤差都處于0.1以下。湖北、江西、內蒙古、山西四個地區的擬合優度和相關性集中在［0.76，0.90］區間內，預測誤差在［0.1，0.5］范圍內。陜西的預測準確率最低僅達到0.58。西藏與其他地區相反，隨機森林和XGBoost模型取得了較好的結果，LSTM模型的準確率較低。

進一步，本文針對預測誤差與收益進行分析。根據公式（1），結合實際情況計算每日的誤差和收益。根據當年風電上網價格與成本確定收益r為367.08元／千瓦，火力發電運行成本w為287.30元／千瓦，懲罰系數k為0.1。

以2018年新疆為例，比較絕對誤差與收益的關系。如圖2展示了部分數據點，預測誤差與收益和成本的變化情況，發現隨著｜ΔPt+1，h｜的減小，收益總體呈上升趨勢，成本逐漸減小。證明了預測誤差小、精確度高的日前預測，能夠增加風電場的收益，對其運營調度產生積極作用。

圖2 預測誤差與電力系統成本與收益

本文希望打通數據—模型—價值這一鏈條，對不同數據的價值進行評估，從而得出在數據中重要的樣本或特征。由于各省數據分布、預測模型均不同，需要分別進行評估。本文選取新疆與遼寧兩省作為實例評估數據價值，兩個省份模型表現較好，且新疆作為風電大省代表西部的內陸城市，遼寧作為東部省份的代表。由于精確計算沙普利值復雜度非常高，本文采用TMC-Shapley方法［26］，使用隨機重抽樣的方式估算各點沙普利值。

3.3 特征的數據價值

本部分將使用沙普利值量化電力系統的數據價值，評估在預測任務中重要性較高的特征。同時本文選取信息熵（香農熵）這一經典統計量作為數據價值衡量的另一個角度，與沙普利值進行對比。在實驗中計算不同特征的沙普利值和Kozachenko和Leonenko［28］提出的估算連續特征信息熵。為了結果的真實性，每個特征至少隨機抽樣3000次，并將計算結果分別Z-score標準化以便于對比。遼寧和新疆兩省數據的計算結果如圖3所示。

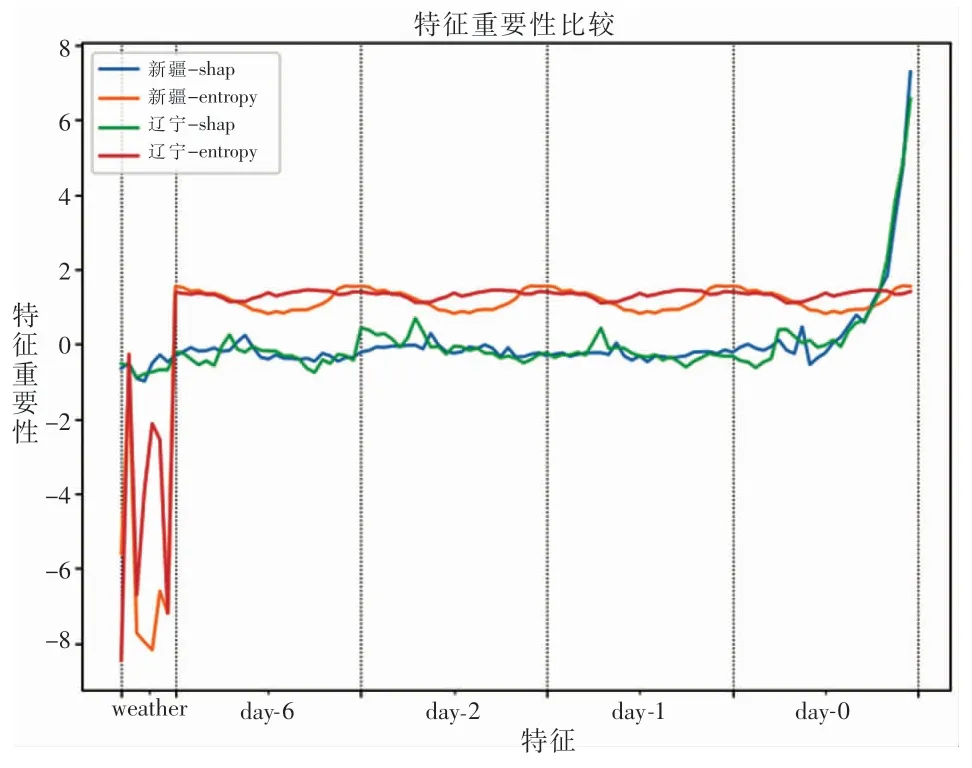
圖3 不同數據特征的價值評估

圖3 中分別列出兩個數據集中不同衡量特征價值的方法比較。橫軸為預測模型使用的特征從左到右可分為5個部分：天氣特征（weather）、一周前發電功率數據（day-6）、近3天發電功率數據（day-2，1，0），縱軸為數據特征價值。如圖所示，信息熵反映出數據一定的周期性，約為24小時，發電功率的波動具有相似性，且天氣數據的價值比較低；而使用沙普利值衡量的結果中，接近預測時間節點的歷史數據價值較高，較為久遠的歷史數據價值在0附近波動，天氣特征的數據價值同樣偏低。本文認為一方面是單一天氣站的數據較為片面，難以體現全省風力狀況，且天氣采樣時間粒度為12小時，對小時級的預測任務貢獻不足。

進一步，本文根據特征數據價值從高到低的順序逐步向模型中加入特征，觀察模型效果變化。如圖4所示，縱軸為電力系統收益損失R*t-Rt，橫軸為按順序加入模型的特征個數。可以看出根據沙普利值（shap）順序加入特征的模型表現強于隨機（random）、熵值（entropy）順序。對比沙普利值與信息熵兩種方法，沙普利值根據效用函數的邊際貢獻計算，受模型影響較大，其高價值特征表現更好。在實踐中，沙普利計算復雜度較高，但能有效提升數據挖掘任務效果，更適用于目的明確的數據特征選擇；而信息熵計算便捷，適合在事前描述數據特征的分散程度，輔助任務不明確的數據評估。

圖4 依次加入特征模型的效果比較

3.4 數據點的數據價值

對特征維度的數據價值進行分析后，本部分重點考察數據點的沙普利值。在風電預測場景下，本文使用TMC-Shapley算法給出參與訓練模型樣本點的數據價值，采取與特征價值相同的方法估算沙普利值，并使用Z-score方法進行標準化。

為了能直觀地展示“低價值”與“高價值”數據的特點，便于“事前”（規避訓練模型）篩選出高／低價值數據，方便電力系統的管理。圖5展示了數據價值處于分布兩極的數據點，左圖為低價值數據，右圖為高價值數據。發現低價值數據在待預測時間點前存在比較突然的趨勢轉折，而這一趨勢轉折很可能是LSTM模型無法捕捉的部分，但這部分數據所體現的特征并不典型，即無法反應數據上風電場功率大部分時間內的變化特點，對模型造成了干擾，這也是其價值較低的原因。而高價值數據則較為“平緩”，能夠對模型預測起到積極作用，幫助模型學習相對可預測的未來趨勢。

圖5 高／低價值時間序列數據比較

類似特征，利用這一順序，本文同樣選取新疆與遼寧的數據，將低價值數據從數據集中按順序去除，觀察模型的表現變化，實驗結果如圖6所示，其中橫軸為模型已經移除數據的比例，縱軸為模型預測導致的電力系統收益損失R*t-Rt。

圖6 依次去除低價值數據點的模型效果比較

對于三種不同的數據去除順序，在依照沙普利值去除低價值數據后，模型的效果反而能夠得到提升。與之相反，信息熵順序在這一實驗中的表現較差，原因可能為信息熵衡量的是“單一數據的信息量”，雖然數據的信息量大，但其信息可能與最終的預測任務不相關，因此不能對最后的預測任務做出正面貢獻。

為驗證沙普利值的有效性，利用遼寧、新疆數據的訓練集驗證沙普利值的噪聲數據檢測效果。通過隨機挑選20%數據，對y施加服從標準正態的白噪聲計算沙普利值識別噪聲數據，如圖7所示，根據計算出的沙普利值由低到高去除數據，在去除數據的比例中，噪聲數據比例顯著高于隨機順序的數據，由此說明沙普利值方法的有效性。

圖7 利用沙普利值識別噪聲數據

利用沙普利值的上述性質，電力系統可以對數據在使用之前進行初步“篩選”，保留“高價值”數據集，從而達到更高計算效率與精度。此外，沙普利值中的低價值數據可視作數據集中含有“噪聲”的數據，該噪聲并非人為添加，而是系統實際運行中的離群點，在數據挖掘中應將其去除。

3.5 電力系統中的數據管理機制設計

在電力系統中數據積累迅速，但數據的使用并非多多益善，從上文算例可以看出，部分低效數據會對模型造成負面影響。因此，有效管理系統內數據能夠提升數字化驅動模式的運行效率，更高效釋放數據中的價值。而具體到電力系統，結合數據價值與數據實時更新的特點，本文給出如圖8所示的高價值數據管理框架。

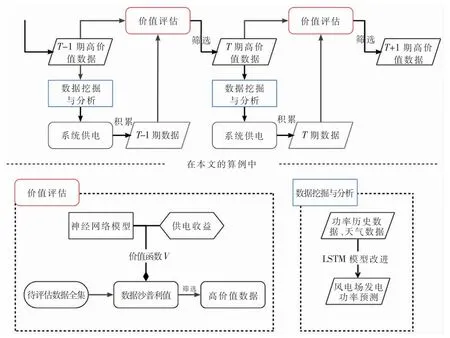
圖8 電力系統高價值數據管理框架

該框架可以使電力系統維護一個數據量較少的高價值數據集，該數據集以提高系統中的數據驅動任務為目標，并能保證數據的實效性，避免使用全量數據，降低數據計算成本。如上述流程圖所示，該框架考量離散時間下的數據更新，下面所屬期限以天為周期，具體步驟如下：

在T期時：

（1）系統擁有上一期留存的高價值數據集合（T期高價值數據），若為初始階段，無高價值數據積累，可以視為空集。

（2）系統根據上述高價值數據進行電力系統所需要的數據挖掘與分析，比如在本文中，使用高價值數據建立功率預測模型，預測T期風電場發電功率，降低平衡供需所付出的額外成本。

（3）系統根據事前功率預測結果完成T期供電與調度任務，獲得系統第T期的數據。

（4）將T期數據與上一期留存高價值數據混合。評估混合數據的價值，確定效用函數，利用數據沙普利值算法或其他方法評估價值，截取價值較高數據點積累本期高價值數據。

在步驟（4）中，并未說明保留數據的最優比例，實踐中可采取如圖6所示數值實驗確定最優數據保留比例。根據沙普利值順序依次去除低價值數據使效用損失先降低后增加，可以根據曲線中的最低點選擇高價值數據集的大小。此外，價值評估模塊中使用的方法并不局限于沙普利值，價值函數與模型預測也可針對不同場景進行遷移，能夠適應不同的應用場景。沙普利值在實際使用時，需要重復計算模型、且高度依賴當前數據集分布、無法泛化到不同的數據集。針對這一不足，本文提出幾點改進思路：

（1）分析算法使用模型結構，嘗試使用不需要計算模型的函數近似原有的效用函數V，降低計算復雜度［29］。

（2）建立數據與其沙普利值的機器學習模型，使沙普利值本身具有泛化能力［30］。

（3）在（2）的基礎上，考慮數據分布的差異，采用遷移學習的思想，將沙普利值泛化到不同分布的數據集中［31］。

4 結論與啟示

電力系統作為重要的數據提供者與應用者，有效評估系統中的數據價值有助于數據的高效利用與數據融通。本文基于各個省份的風力發電功率歷史數據建立各省的24小時風電場發電功率多輸入—多輸出預測模型，取得了良好的預測效果。進一步，結合電力系統背景，建立數據—模型—收益的鏈路聯系；使用TMC沙普利值方法評估電力系統的特征與數據價值，并通過實驗證明其有效性，提出了一種能夠在預測場景中確定數據價值的理論框架，且該框架能夠遷移到其他場景下。在電力系統預測場景下的實驗表明該框架能夠剔除低價值數據／特征有助于提升模型表現，降低計算成本。

隨著全球數字化轉型不斷推進，數據在推動經濟增長中起到的作用也將愈發明顯。電力系統擁有海量數據，數據管理是其關心的重要問題，本文在電力系統中對數據價值進行了有效評估，使數據價值評估方式的具體應用落地。本文通過數值實驗發現在功率預測場景下，將數據估值方式應用到場景中，適當對數據進行動態篩選和更新，能令電力系統維護一個較為高價值的“數據集”，節約數據的儲存、管理、計算成本，提升數據使用效率。此外，高／低價值數據雖仍屬于事后價值評價方法，但能從評估結果中提煉高／低價值數據的特點，對事前數據價值評估進行指導。在算例研究中，“平緩”可能為數據高價值的因素。在其他情況下，不同的數據類型與任務可能使數據的“高價值”特征不同，比如：回歸任務中因變量與自變量相關性更強的數據；圖片識別場景下更清晰的圖片；分類任務中更接近分類超平面的數據。總體而言，高價值數據點通常更能體現模型挖掘的知識。而且，通過建立數據點與其價值的預測模型也能進一步尋找數據的價值規律，有助于將評估事前價值、數據價值評估泛化。本文在3.5節中給出數據價值評估驅動下的電力系統數據管理機制設計，將數據估值與挖掘進行有機結合，為電力系統中的數據治理提供了新的思路。