一種基于改進布谷鳥算法的極值搜索控制方法及應用*

黃政雨 ， 白玉婷

（1.杭州電子科技大學經濟學院，浙江 杭州 310018；2.黔南民族師范學院計算機與信息學院，貴州 黔南州 558000）

0 引言

化石燃料的減少和環境污染的加劇是當今世界面臨的重要發展問題[1]。太陽能的利用具有成本低、環境友好、零碳排放和自然資源豐富等優點，受到廣大科研人員的青睞[2]。由于不確定的環境影響，太陽能電池功率-電壓（P-V）曲線是非線性的，需要一個最大功率點跟蹤（MPPT）控制器確保在任何環境下太陽能電池都保持最大功率工作[3]。

極值搜索控制方法（ESC）一般針對不確定復雜動力學模型，通過動態調整動力學參數和反饋控制實現這些系統的最優控制[4]。太陽能光伏系統所處外界環境復雜，最優穩態模型不確定，傳統最優控制難以應用，因此可采用極值搜索控制方法實現動態環境下的最大功率點跟蹤（MPPT）控制[5]。

傳統MPPT 控制技術，例如增量電導法（INC）、擾動和觀測方法（P&O）基于梯度下降原理，無法區分局部最優和全局最優值[6]。基于智能優化的MPPT控制技術，例如蟻群算法（ACO）、灰狼算法（GWO）等由于其隨機性的特點，動態性能參差不齊且系統振蕩過多，工業應用困難[7]。課題組研究了一種基于改進布谷鳥算法（CS）的極值搜索控制方法，并進行了仿真實驗以驗證方法性能。首先，介紹控制系統動力學模型；其次，介紹基于改進布谷鳥算法的極值搜索控制方法；再次，進行實驗測試；最后，對全文進行總結。

1 太陽能光伏系統動力學模型

一般的太陽能光伏系統由三個部分組成，即太陽能電池、DC-DC 轉換電路和MPPT 控制器。太陽能電池可以通過電流源、二極管和電阻進行建模[8]，數學模型如式（1）所示：

式中，Iph(t)為太陽能電池發電產生的動態電流，Is為二極管飽和電流，V(t)為太陽能電池輸出電壓，Rs為串聯電阻，A、Vt為電路理想系數，可視為常數。DC-DC 斬波電路數學模型已有研究人員研究，如式（2）所示[9]：

綜上，可得太陽能光伏系統動力學模型，如式（3）所示：

式中，f、J均為系統狀態變量、輸出變量的平滑映射函數，其中J為不確定函數。而且由于能量守恒定律限制，該系統為自穩定系統且對于任意的J皆存在u*，使得y=y*，y*≥y(t)。

2 基于改進布谷鳥算法的極值搜索控制方法（ICS）

布谷鳥搜索算法通過模擬布谷鳥的寄生育雛習性有效求解優化問題[10]。布谷鳥采用一種迭代方式由一個巢隨機飛向另一個巢，尋找安全孵化幼崽概率最高的巢穴。如果宿主發現了布谷鳥蛋，則會將其扔掉或者棄巢。布谷鳥算法利用Levy 飛行實現布谷鳥由一個巢飛向另一個巢的迭代，如式（4）所示：

式中，i是迭代次數，k=1,2,…,ss是當前搜尋群體中的個體排序，ss是搜索群體大小，α是搜索步長，u和v是基于均勻分布的隨機矩陣，如式（5）所示：

其中，u和v的方差如式（6）所示：

每一次迭代后布谷鳥蛋均有被宿主發現的危險，被發現概率為p。若被發現，則布谷鳥會飛向隨機巢并重新迭代。為加快算法收斂速度，改進布谷鳥蛋被發現后的迭代算法，布谷鳥不飛向隨機位置而繼續向當前全局最優dbest迭代，如式（7）所示：

這樣就使得算法向當前最優值更快速移動，提升了算法的收斂速度。假設系統擾動響應速度慢于系統控制器輸入調整速度，系統輸入調整速度慢于系統輸出響應速度，則在調節時間內，可認為系統外界擾動為常值，在該時間尺度下系統模型為定長確定模型。以該時間尺度為采樣和控制調節時間，在該時間尺度利用改進布谷鳥算法實現優化控制，則可得到系統離散控制率u(k)。

由于物理系統為連續系統，而改進布谷鳥算法為離散算法，因此需將離散的布谷鳥算法轉變為連續系統的控制器。基于零階保持器的原理，在采樣的兩個時刻之間，控制輸入保持不變，則可得離散-連續的極值搜索控制方法，如式（8）所示：

3 數值仿真

本文利用MATLAB 建立了太陽能光伏系統動力學模型，該模型模擬環境溫度為20 ℃，PWM 頻率設置為100 kHz，采樣頻率為0.001 s，模擬失配條件下的光伏發電系統輸入PWM 信號占空比到輸出功率的平滑映射函數。該函數呈現多峰特性，具有4 個極點且最大輸出功率為570 W。本文利用Runge-Kutta 方法求該仿真模型的數值解。

實驗測試了在相同情況下傳統CS 算法和本文提出的ICS 算法的性能，算法仿真結果如圖1 所示。傳統CS 算法和本文提出的ICS 算法均能找到全局最優值，但本文提出的ICS 算法找到的全局最優值為559.74 W，傳統CS 算法找到的全局最優值為522.04 W，且在穩定后傳統CS 算法存在小幅度振蕩，而本文提出的ICS 算法不存在穩態振蕩，因此本文提出的ICS 算法穩態性能遠優于傳統CS 算法。傳統CS 算法在0.078 3 s 后收斂，而本文提出的ICS 算法在0.025 5 s 處實現收斂，本文提出的ICS 算法調節時間三倍優于傳統CS 算法。傳統CS 算法存在大幅振蕩10 余次，小幅振蕩20 余次，而本文提出的ICS 算法僅存在大幅振蕩兩次，小幅振蕩一次，算法動態性能遠優于傳統CS算法。

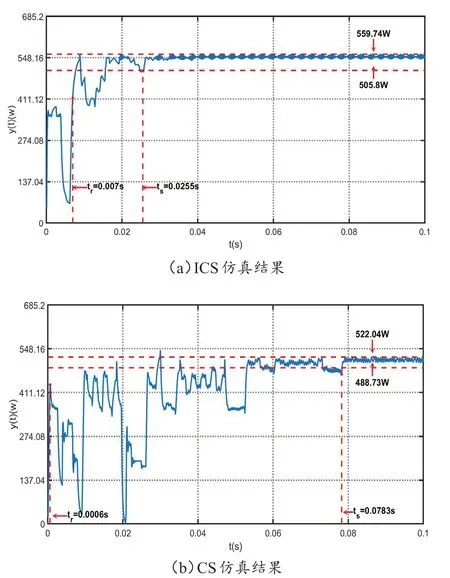
圖1 算法仿真結果

綜上所述，本文所提出的ICS 算法在仿真研究中動態性能和穩態性能遠優于傳統CS 算法，其在調節時間、振蕩水平和極值搜索能力等方面均性能優越。

4 結論

首先，基于太陽能光伏系統的物理機理和控制電路，課題組提出了一種動力學模型以解釋和概括太陽能光伏系統；基于極值搜索控制機理，課題組提出了基于時間尺度的假設，并驗證了太陽能光伏系統極值搜索的可能性。

其次，課題組提出了一種基于改進布谷鳥算法的極值搜索控制方法，在采樣時間內完成系統的最優控制，并基于離散-連續控制方法實現連續動態太陽能光伏系統的最優控制。該方法結構簡單，動態性能和穩態性能卓越，且實現了離散-連續控制轉換，可用于數字控制電路。

最后，課題組通過數值仿真將提出的算法在失配條件下與傳統CS 算法進行比較，以驗證算法追蹤全局最大功率點（GMPP）的能力。結果顯示，課題組提出的ICS 算法可以非常精準地找到和追蹤GMPP，其動態性能和穩態性能均遠優于傳統CS 算法，其中算法穩態振蕩全部消除，算法找到的極值輸出功率也大于傳統CS 算法，算法調節速度提升了約兩倍，算法振蕩水平大幅降低。