高功率脈沖對接地傳輸線耦合的FDTD方法

王一凡，田 煒*，王云康

（1.延安大學 物理與電子信息學院，陜西 延安 716000；2.榆林市生態環境局 固體廢物管理中心，陜西 榆林 719000）

隨著高功率電磁脈沖源在實際生活中日益廣泛地使用，電子設備面臨的電磁環境越來越復雜，電磁脈沖將會通過散熱孔、連接電纜、外部天線等對設備內的電子元件產生電磁干擾［1-5］。即使對電子設備進行了電磁兼容設計，但若用于連接電子設備的傳輸線并沒有防護措施，特別是直接暴露在外的傳輸線受到電磁脈沖照射時，就會在線路上產生電磁耦合，電磁能量將通過傳輸線進入設備內部進行電磁攻擊，進而損毀設備的敏感電子元件［6-9］。因此，開展電磁脈沖對傳輸線的瞬態耦合問題研究對于線路和設備的防護具有重要意義。

近年來，有關電磁波對傳輸線的耦合研究取得了一系列進展。AGERWAL等［10］采用時域有限差分（FDTD）法研究了不考慮背景的多導體傳輸線電磁耦合問題，并給出了計算中的穩定性條件；ERDIN等［11］采用SPICE等值電路法研究了電磁脈沖激勵多導體傳輸線的電磁耦合問題；SHINH 等［12］提出了一種快速的閉合SPICE 模型，計算了接地多導體傳輸線的瞬態電磁耦合，分析中忽略了背景的電磁貢獻。考慮接地背景反射的電磁耦合研究，近年來也取得了一系列進展，DIENDORFER［13］采用傳遞電流模型給出了雷達脈沖激勵場，根據鏡向原理解決了接地平面的電磁貢獻，并運用有限差分方案研究了傳輸線終端負載的電磁耦合問題；REN 等［14］運用FDTD方法研究了雷電脈沖對接地傳輸線的電磁耦合問題，其中，背景反射場采用電磁場FDTD 來計算，而電磁耦合通過傳輸線FDTD 來分析。本文針對接地傳輸線問題，采用了一種頻域反射與傅里葉變換相結合的方案來分析地面背景的電磁反射，再運用FDTD 方法計算了高功率電磁（HPEM）脈沖激勵多導體傳輸線的電磁耦合，數值計算得到了多導體傳輸線接地負載上的時域感應電壓，并分析了直接照射波參數、負載參數對電磁耦合的影響規律。

1 基本原理

1.1 入射波的引入

入射波激勵下的多導體傳輸線模型如圖1 所示，近地平面上的雙導體傳輸線沿著z軸放置，長度為L，傳輸線終端的接地電阻分別為RS1、RL1、RS2、RL2。

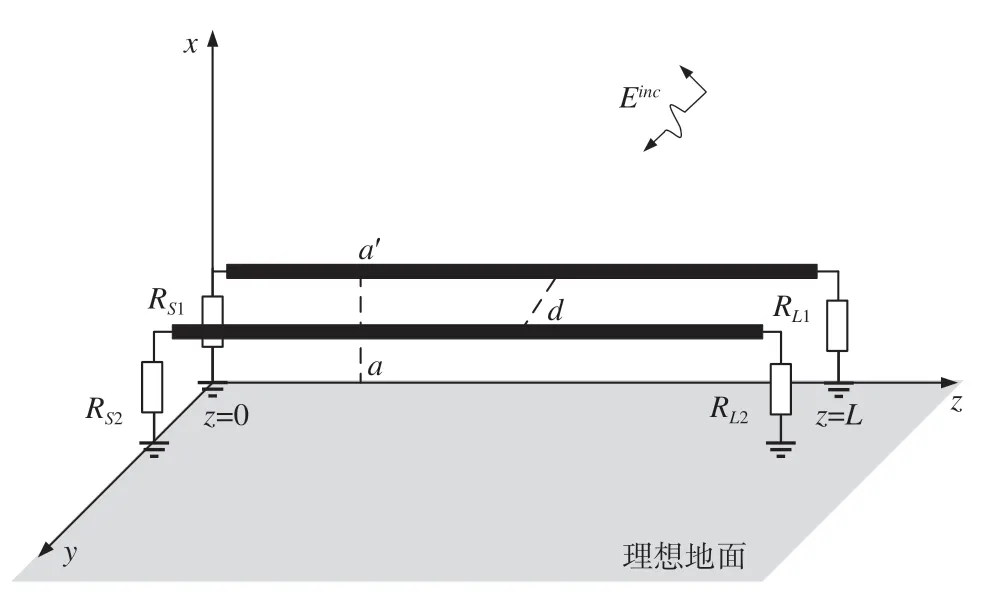
圖1 入射波激勵下的多導體傳輸線幾何示意

由于所研究的導體傳輸線長度很短，且傳輸線本身損耗極小，可將其視為無耗導體傳輸線。空間電磁場對雙導體傳輸線的電磁耦合可以通過傳輸線方程來描述。在入射場激勵下，多導體無耗傳輸線電報方程［15］可表示為

其中，電壓V(z，t)和I(z，t)分別為電壓矩陣和電流矩陣，L和C分別是單位長傳輸線的分布電感矩陣和電容矩陣，ET和EL分別是外場激勵分布的電壓源和電流源。

入射波矢量指向直角坐標系的坐標原點，它與x軸的夾角為θP，在yOz平面上的投影與y軸的夾角為φP，如圖2A 所示。入射波的極化采用a→θ和a→φ為單位矢量的局部坐標來顯示，具體見圖2B。

圖2 入射波的入射角和極化角圖解

根據上述規定，在時諧場情形，傳輸線直接照射平面波可表示為

其中，E0為照射場幅值分別為直角坐標系x、y和z方向上的單位向量，ex、ey、ez分別為單位入射場在三坐標軸上的分量，可表示為

考慮傳輸線置于理想導體接地平面上方，入射波不可透入理想導體接地平面內部，只在其表面上發生反射，根據菲涅耳反射定律［16］可知RTE=-1，RTM=1。因此，傳輸線的直接照射場和背景反射場分別為

本文僅考慮雙導體傳輸線問題，以下分析以y=0 面內的傳輸線為例進行。在式（1）中，等效激勵源ET可表示為

類似地，EL可表示為

其中，d為傳輸線相對地面的距離，對于近地傳輸線模型，有sin(βxd)/(βxd) ≈1。將其代入式（7）和（8）后，通過逆傅里葉變換可得

其中，vx、vy、vz表示沿各坐標軸的傳播速度，這里

1.2 傳輸線的離散

下面將基于FDTD 方法，對傳輸線方程進行離散。電壓節點和電流節點在空間分布相距1/2 網格，提取時刻相距1/2 時間步，其節點位置和時間取樣如表1所示［17］。

表1 FDTD中電流、電壓空間和時間取樣

將式（1）中的空間偏導和時間偏導均采用中心差分近似，通過時間步整理后，可得到電壓和電流的時間推進公式分別為

1.3 計算域的截斷

在傳輸線的FDTD 分析中，需在終端設置吸收邊界條件對計算區域進行截斷［17］。本文采用廣義戴維南定理結合前后向差分的方案來實現。用IS表示傳輸線左端(z=0)的電流，IL表示右端(z=L)電流，圖3 為傳輸線左右兩端的電壓和電流在空間和時間上的離散示意圖以及等效電路圖。

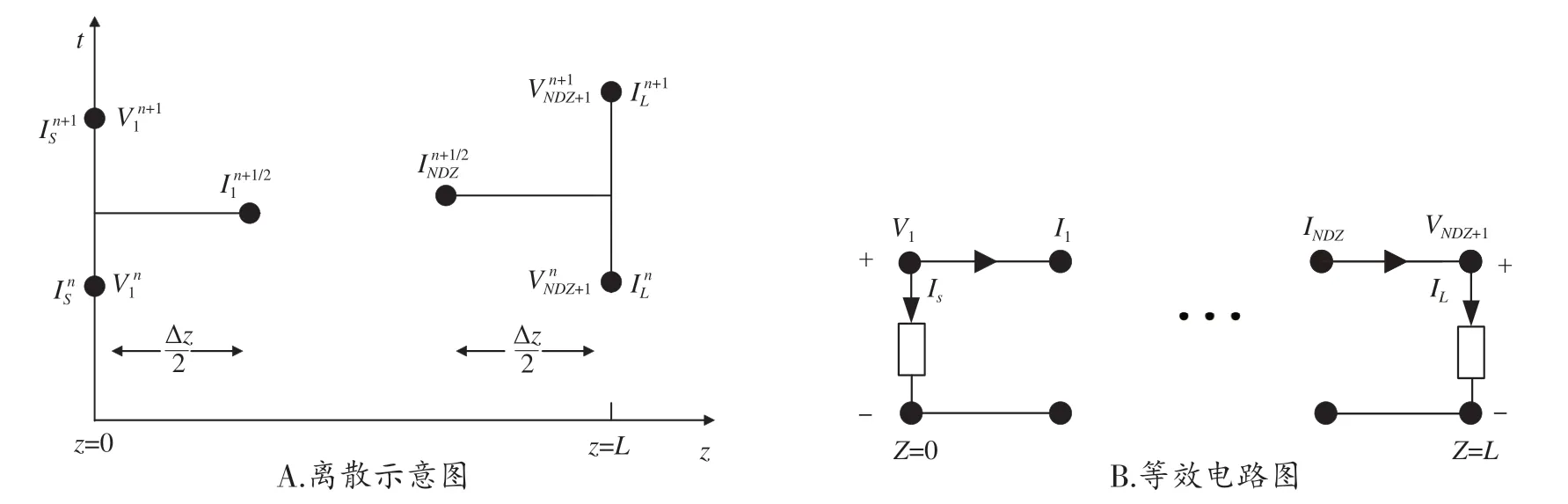
圖3 傳輸線在左右端口空間和時間的離散示意和等效電路圖

根據廣義戴維南定理［16］可得

將式（15）帶入式（14），可得終端吸收邊界條件為

其中，V1和I1是傳輸線左端口處的電壓和電流，VNDZ和INDZ是傳輸線右端口處的電壓和電流，RS和RL分別為傳輸線左右端口的負載阻抗，L=NDZΔz。

2 數值結果與討論

考慮到傳輸線模型受到以下HPEM 高斯脈沖激勵，

其中，E0=50 KV，t0=0.6 ns，T=0.48 ns。

在以下的計算中，若無特別說明，取傳輸線長度為10 m，半徑為0.38 mm，導線中心之間的距離為1.14 mm。傳輸線端口負載分別選取為RS1=50 Ω、RL1=1 000 Ω、RS2=10 000 Ω、RL2=100 Ω，單位長傳輸線分布L和C矩陣分別為

在矩陣L和C中，主對角線元素為傳輸線的自感和自容系數，其他元素為傳輸線的互感和互容系數，FDTD 法將空間離散為NDZ=1 000 個網格，每個等間距網格長度Δz=l/NDZ=1 cm（l為傳輸線的長度），總時間步為NDT=10 000，時間步長Δt=總計算時間/NDT=0.03 ns。

2.1 入射波極化角對傳輸線端口瞬態響應的影響

以線極化為例，保持其他參量設置不變，僅將入射波的極化角θe分別設置為30°、60°、90°，分析入射波不同極化方向對傳輸線端口響應的影響，其結果如圖4 所示（VL和VR分別表示傳輸線左端口和右端口的電壓瞬態響應）。可以看出，當改變入射波的極化角時，傳輸線端口的瞬態響應波形幾乎相同，只是峰值大小不同。這是由于隨著極化角度的減小，電場在傳輸線橫向方向上的分量逐漸減小，從而入射波的電磁場強度幅值不斷減小，最終使得線纜終端的響應峰值不斷減小。由此可見，傳輸線上的瞬態響應幅值隨著入射波極化角的減小而減小。

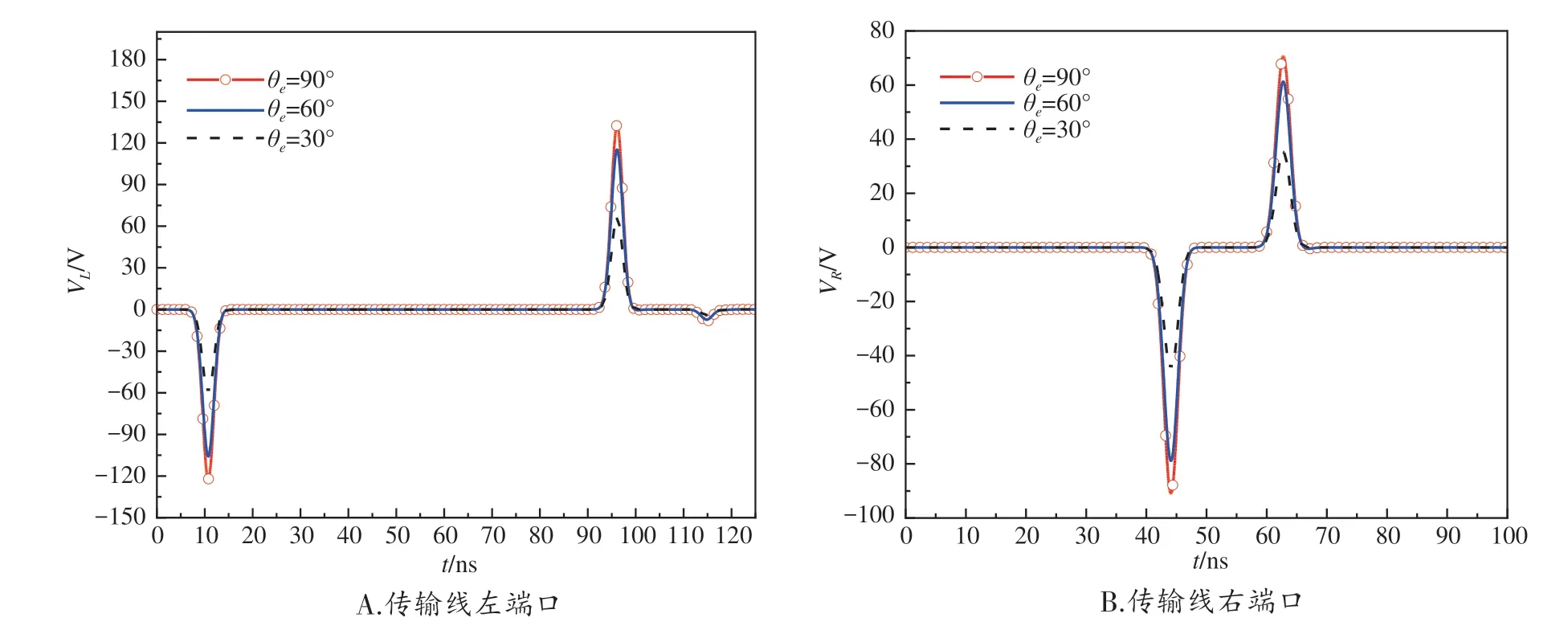
圖4 傳輸線端口在不同極化角下的瞬態響應

2.2 入射波入射角對傳輸線端口瞬態響應的影響

將入射角θp分別設置為30°、60°、90°，分析入射波的入射角對傳輸線端口的影響情況，其結果如圖5所示，其余參數取值與圖4相同。可以看出，傳輸線端口的電壓響應在不同入射角下的波動情況大致相同，只是峰值大小和位置有所不同。當入射角度逐漸增大時，響應峰值也有所增大，在入射角為90°時最大。這是由于隨著入射角度的增加，電場在傳輸線縱向方向上的分量逐漸增加，從而入射波的電磁場強度幅值不斷增加，最終使得線纜終端的響應峰值增加。因此，傳輸線上的瞬態響應幅值隨著入射角度的增加而增加。

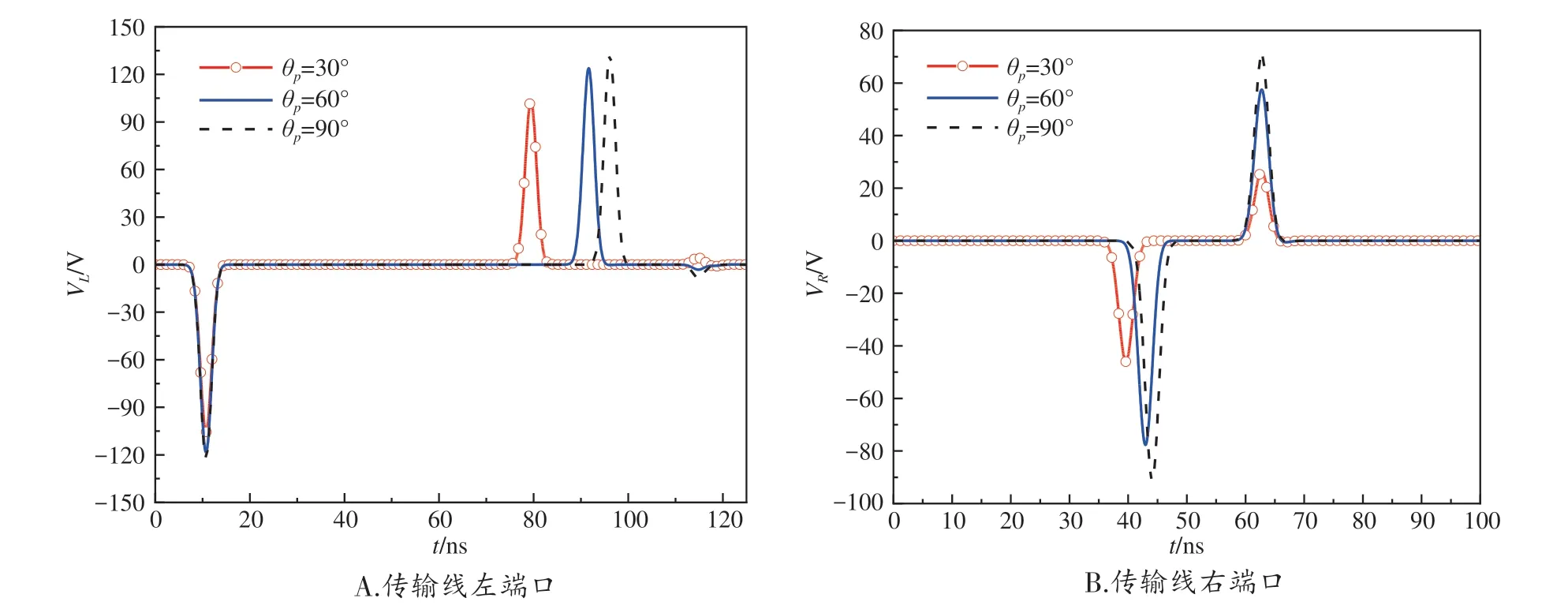
圖5 傳輸線端口在不同入射方向下的瞬態響應

2.3 不同電阻值對傳輸線端口瞬態響應的影響

由圖1 可知，傳輸線兩端的電阻值分別記為RS1、RL1、RS2、RL2。入射波參數設置為θe=60°，θp=60°，φp=-90°，取負載阻值分別為500 Ω、1 000 Ω、2 000 Ω，分析傳輸線在不同負載阻值下受到入射波激勵時，端口瞬態響應的情況，其結果如圖6 所示。可以看出，當改變傳輸線終端的負載阻值時，傳輸線端口的瞬態響應波形幾乎相同，只是峰值大小有所差異。隨著終端負載阻值的增大，端口的瞬態響應峰值也隨著增大。這是因為當傳輸線受到一定頻率的電磁波照射時，會在傳輸線上形成感應電流，并通過線纜的阻抗轉化為感應電壓。由此可以看出，傳輸線上的電壓響應幅值隨著終端負載阻值的增加而增加。

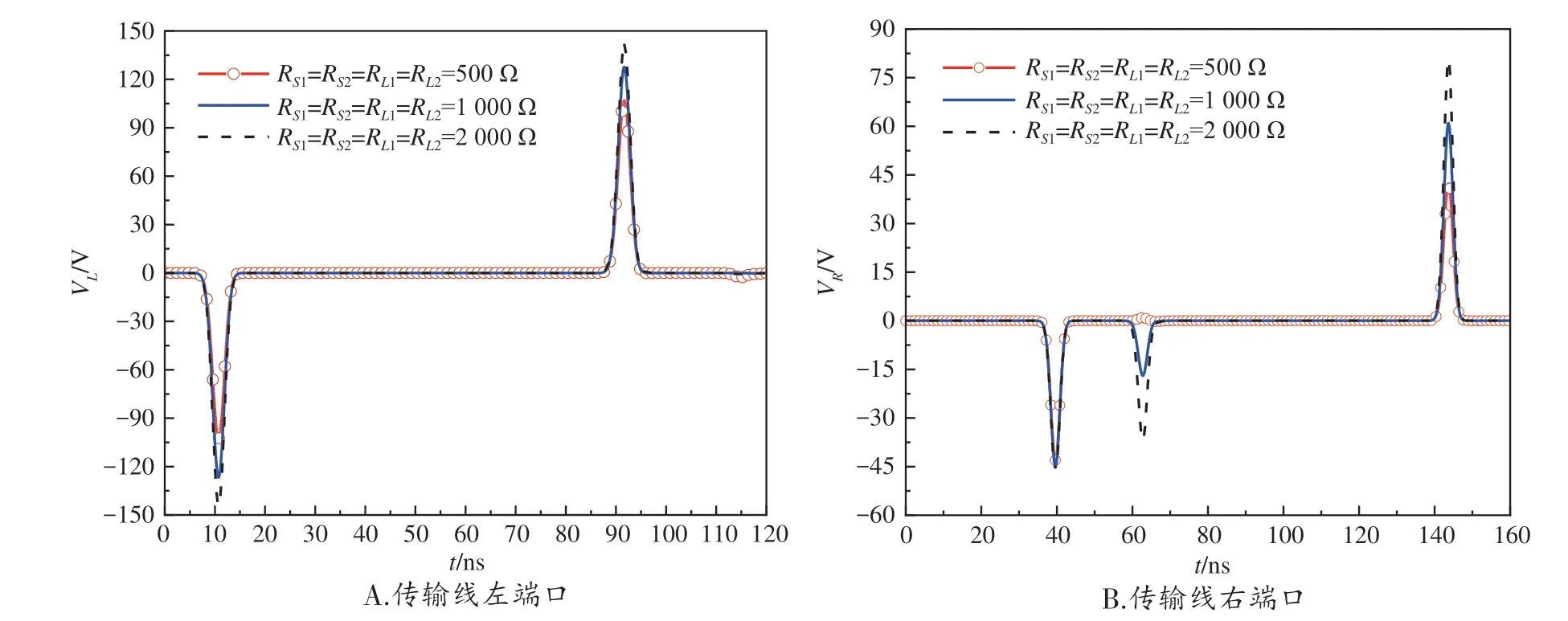
圖6 傳輸線端口在不同電阻值下的瞬態響應

3 結束語

本文在傳輸線方程的基礎上，采用FDTD 方法計算了HPEM 高斯脈沖對具有接地負載的多導體傳輸線的時域電壓響應。本方法在整個傳輸線上進行建模，能夠靈活地選取觀察點，對任意位置的耦合特征進行分析。在數值模擬過程中充分考慮了地面背景的反射問題，通過數值計算得到了端口電壓隨入射波照射方向及終端負載變化的基本特性。數值結果對在有外界電磁干擾下，分析設備連接線對終端設備的電磁攻擊提供了重要的參考價值。下一步將重點開展高功率電磁波對接地有耗傳輸線的電磁耦合研究。