具有非線性能量阱的雙層隔振系統抗沖擊分析

陳 森，朱 翔，3，*，李天勻，3，陳樹鑫

（1.華中科技大學 船舶與海洋工程學院，湖北 武漢 430074；2.華中科技大學 船舶和海洋水動力湖北省重點實驗室，湖北 武漢 430074；3.上海交通大學 高新船舶與深海開發裝備協同創新中心，上海 200240）

0 引言

近些年來，非線性能量阱（Nonlinear Energy Sink，NES）作為一種被動控制技術的減振裝置，以其構造簡單、減振頻帶寬、魯棒性好等優點逐漸在工程領域中得到廣泛關注[1]。非線性能量阱通過靶向能量傳遞（Target Energy Transfer，TET），能夠快速、單向不可逆地俘獲主體結構的振動能量，并通過自身的阻尼元件耗散能量。

目前，NES 技術正逐漸被應用到各個工程領域。LUO 等[2-3]通過爆炸試驗研究了具有NES 的九層建筑結構的抗沖擊性能，結果表明：NES 可以快速減低結構的整體響應。樓京俊等[4-5]針對艦船垂向振動減振需求，設計了一種可垂向承載的柔性鉸鏈型NES 裝置，試驗結果表明：該裝置具有較好的寬頻減振效果。此外，該技術還廣泛應用于機械工程[6]、能量采集[7]等領域，但目前該技術在船舶領域相關的工作相對較少。

隨著導彈、水中兵器的快速發展，爆炸當量與沖擊持續時間顯著增加，導致艦船面臨著嚴峻的沖擊環境。對于艦船隔振裝置沖擊防護，許多學者開展了大量的研究工作。蘇智偉等[8]提出了一種含負剛度動力吸振的混合隔振系統，為高傳遞損失抗沖器的設計有著借鑒意義。LEDEZMA-RAMIREZ 等[9]通過切換隔振器的剛度，提出了一種半主動開關控制策略，這種半主動控制系統優于線性被動系統。FRANCISCO 等[10]提出了一種具有低動態剛度的隔振系統，與線性系統相比，該系統有利于改善沖擊隔離。

本文旨在探索NES 技術對艦船設備抗沖擊防護效果。首先建立了具有NES 的雙層隔振系統動力學模型，利用三折線沖擊譜來模擬基座受到水下爆破時的沖擊波，并通過Runge-Kutta 法計算系統的瞬態響應，通過能量分析法討論了非線性剛度、阻尼、附加質量對設備的抗沖擊效果的影響。

1 理論模型

雙層隔振系統的隔振效果優于單層隔振系統，被廣泛作為艦船機電設備的隔振裝置。本文研究的非線性能量阱雙層隔振系統模型示意圖如圖1所示。圖1（b）中，基座的質量為M，通過線性剛度k1，阻尼c1與中間質量m1相連；中間質量m1通過線性剛度k2，阻尼c2與設備m2相連。NES 裝置通過立方非線性剛度kN及阻尼cN與附加質量m3耦合連接。在基座上施加雙峰正弦加速度沖擊波a。

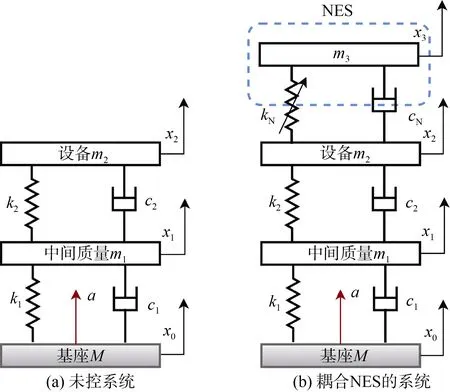
圖1 雙層隔振系統計算模型Fig.1 Calculation model of two-stage vibration isolation

根據牛頓第二定律，具有非線性能量阱的雙層隔振系統動力學方程為：

式中，x0、x1、x2、x3分別為系統的位移。

圖1（a）中的未控雙層隔振系統動力學方程與圖1（b）描述的方程類似。本文采用Runge-Kutta法求解系統的瞬態響應。

當艦船受到水下爆破沖擊時，傳遞到設備的響應在頻域上表現為三折線沖擊譜（位移–速度–加速度）。通過各種波形的組合才能得到三折線沖擊譜，這與一般的機械沖擊不同。其中最大譜位移、最大譜速度、最大譜加速度分別為d0、V0、A0。考慮到系統在受沖擊時的譜跌效應，需要將實際沖擊響應譜轉化為雙峰正弦波信號，可表述為

其中雙峰正弦波的參數為

給定沖擊譜d0=0.03 m，V0=2 m/s，A0=1 000 m/s2下的雙峰正弦加速度沖擊波如圖2所示，本文以該沖擊波分析非線性能量阱對雙層隔振系統的抗沖擊影響。

圖2 雙峰正弦加速度沖擊波Fig.2 Double peak sine acceleration shock wave

2 系統抗沖擊特性分析

雙層隔振系統的參數分別取為：基礎M=100 kg，m1=0.4 kg，m2=1 kg，k1=7 000 N/m，k2=5 000 N/m，c1=3 N·s/m，c2=5 N·s/m。非線性能量阱參數為：kN=1×106N/m3、cN=5 N·s/m、μ=10%，其中μ=m3/（m1+m2）。

本文首先對比了機械設備在雙峰正弦加速度沖擊波下的相對位移與絕對加速度，如圖3所示。從圖3中可見，在沖擊后的100 ms 內，NES 對設備抗沖擊性能的改善作用有限；但隨著時間的增長，附加在設備上的NES 有效控制了其相對位移與絕對加速度。

圖3 機械設備的沖擊響應對比Fig.3 Comparison of shock response of equipment

本文進一步采用能量分析法來討論分析NES 非線性剛度kN、阻尼cN和質量比μ對設備的抗沖擊性能的影響。設備的瞬時機械能可以寫為

在時間t內存儲在設備的總能量可以寫為

下面定義了2 個評價參數來評估NES 的抗沖擊效果，即

式中：Eu為未控系統設備的瞬時機械能；En為耦合NES 系統設備的瞬時機械能；Wu為未控系統設備在時間t內的總能量；Wn為耦合NES 系統設備在時間t內的總能量。

通過NES 阻尼耗散的總能量可以寫為

上文定義了3 個評價參數η1、η2、Wd來評估NES 的抗沖擊效果，其中η1、η2越小，Wd越大，說明NES 抗沖擊效果越好。

保持NES 的參數不變，機械設備的瞬時機械能如圖4所示。從圖4可見，未控系統的瞬時機械能先是快速增大，沖擊結束后，則是在震蕩中緩慢下降；耦合NES 設備的瞬時機械能則可以快速下降，在500 ms 左右幾乎為0。

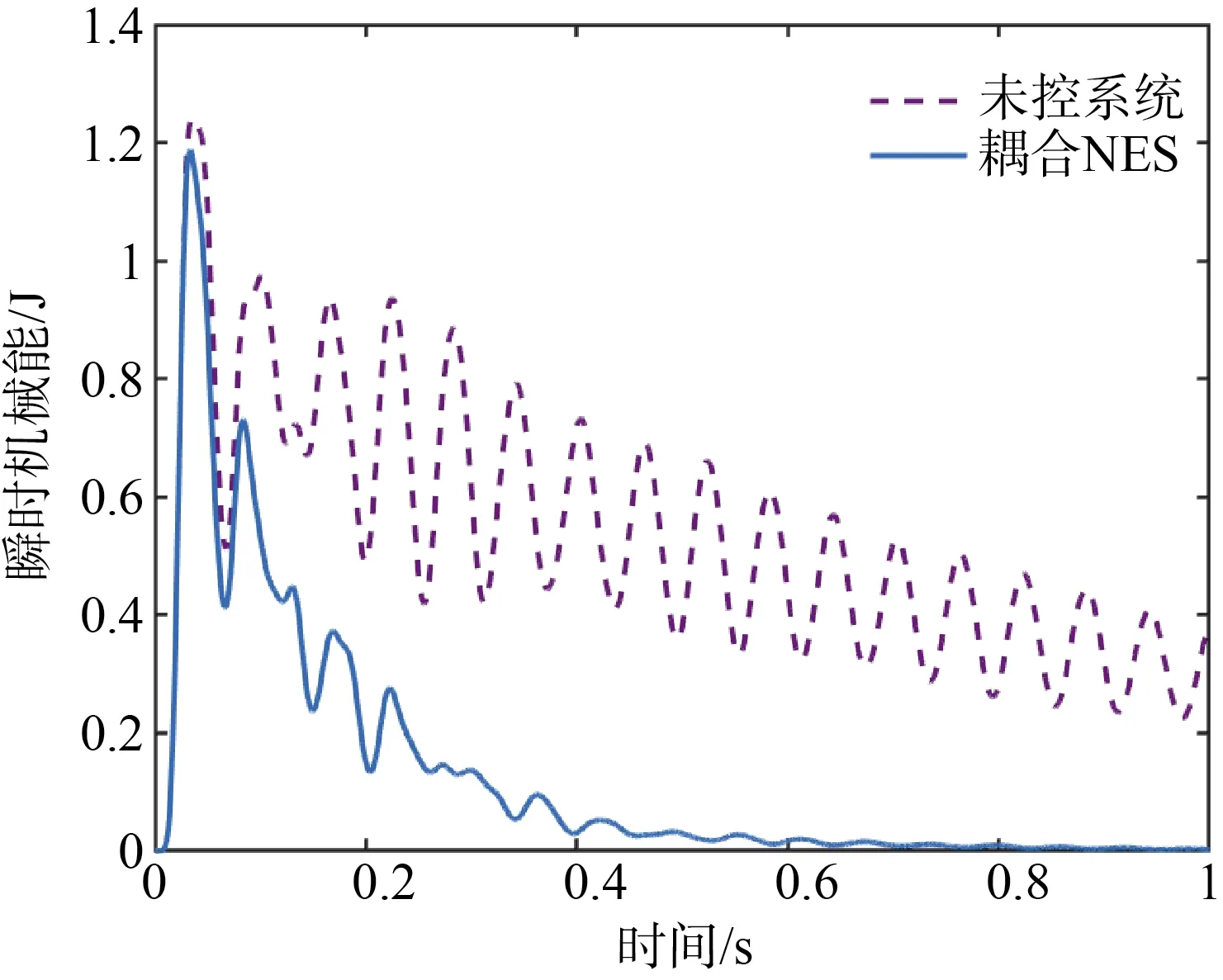
圖4 機械設備的瞬時機械能對比Fig.4 Instantaneous mechanical energy of equipment

保持NES 非線性剛度kN、阻尼cN不變，研究質量比μ對評價參數η1、Wd的影響，如圖5所示。從圖5（a）中可見，在沖擊后的100 ms 內，增大質量比μ對設備抗沖擊性能的改善作用有限；當質量比μ較小時，在沖擊后的較長時間內，η1依然很大；當質量比μ較大時，η2可以快速下降10%以下。從圖5（b）中可見，選取適當的質量比μ可以使得NES 阻尼耗散的能量Wd快速增大。

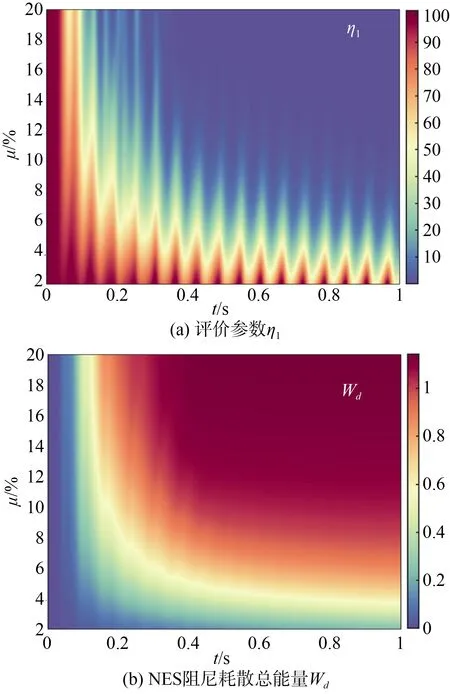
圖5 質量比μ 對抗沖擊效果的影響Fig.5 Effect of mass ratio μ on the impact resistance effect

保持NES 質量比μ、阻尼cN不變，研究非線性剛度kN對評價參數η1、Wd的影響，如圖6所示。從圖6中可見，非線性剛度kN存在著一個最優值，使得η1最小、Wd最大；當非線性剛度kN較大時，會惡化NES 的抗沖擊效果（η1>100%）。保持NES質量比μ、非線性剛度kN不變，研究阻尼cN對評價參數η1、Wd的影響，如圖7所示。從圖7中可見，阻尼cN也存在著一個最優值，使得η1最小、Wd最大；當阻尼cN較小時，在沖擊后的400 ms 內，此時的η1較大，不利于改善設備的抗沖擊性能。

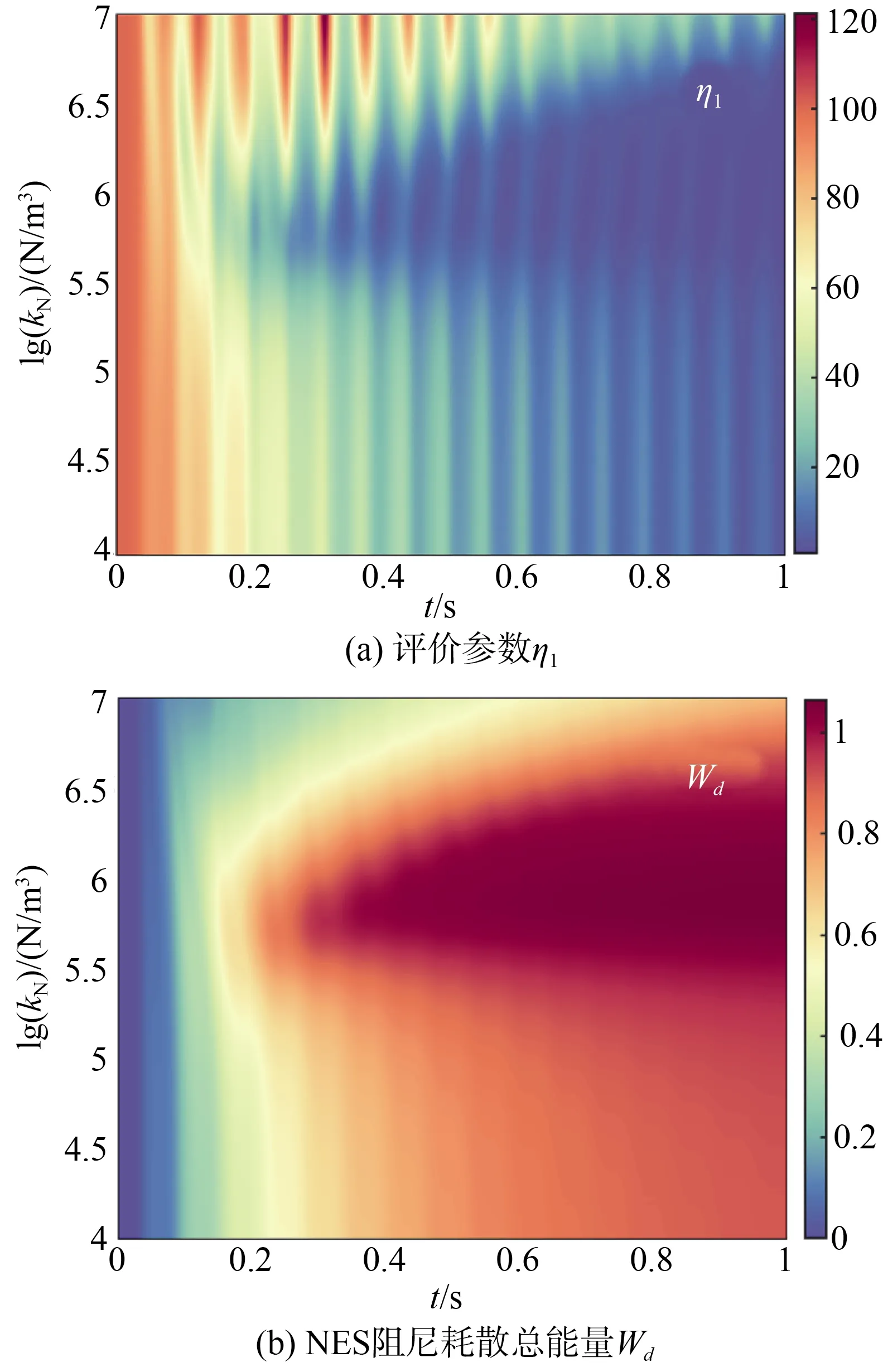
圖6 非線性剛度kN 對抗沖擊效果的影響Fig.6 Effect of nonlinear stiffness kN on the impact resistance effect

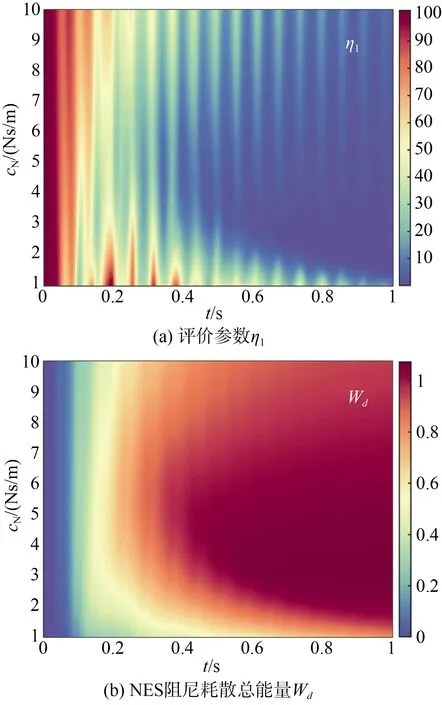
圖7 阻尼cN 對抗沖擊效果的影響Fig.7 Effect of damping cN on the impact resistance effect

下面進一步研究NES 質量比μ、非線性剛度kN、阻尼cN同時對抗沖擊效果的影響。為此，本文分別計算了沖擊后100 ms、500 ms 內的η2與Wd，來評估其對抗沖擊效果的影響，二維等高線圖分別如圖8、圖9所示。

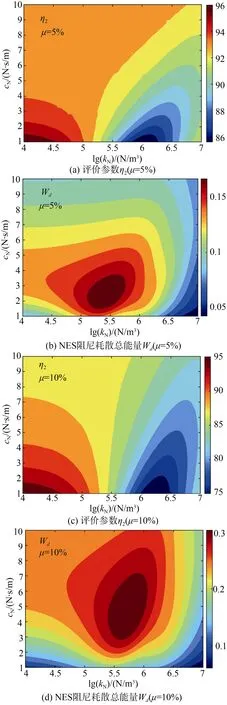
圖8 沖擊后100 ms 內NES 參數對抗沖擊效果的影響Fig.8 Effect of NES parameters on the impact resistance effect within 100 ms after the impact

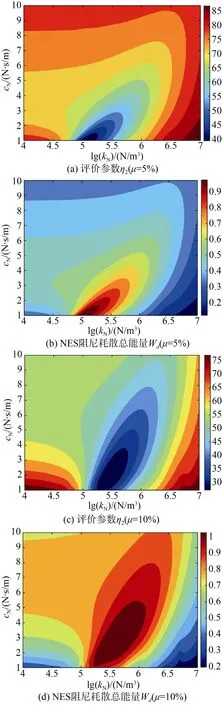
圖9 沖擊后500 ms 內NES 參數對抗沖擊效果的影響Fig.9 Effect of NES parameters on the impact resistance effect within 500 ms after the impact

從圖8中可見，NES 非線性剛度kN、阻尼cN對η2、Wd的影響規律不同，其對應的最優參數范圍不同。從圖8（a）、（b）中可見，當質量比μ較小時（5%），在最優參數范圍內，η2約為86%，Wd僅約為0.15 J，抗沖擊效果不佳；從圖8（c）、（d）中可見，增大質量比μ（10%），在最優參數范圍內，η2約為75%，Wd約為0.3 J，抗沖擊效果得到了一定的改善。從圖9中可見，隨著時間的增長，NES 非線性剛度kN、阻尼cN對η2、Wd的影響規律相似。從圖9（a）、（b）中可見，當質量比μ較小時（5%），在最優參數范圍內，η2約為40%，抗沖擊效果良好；從圖9（c）、（d）中可見，增大質量比μ（10%），在最優參數范圍內，η2下降到了30%以下，Wd約為1 J，且最優參數范圍更大，其魯棒性較好。

3 結束語

本文分析了具有非線性能量阱的雙層隔振系統抗沖擊效果。通過能量分析法討論了非線性能量阱參數對其抗沖擊性能的影響。針對本文給出的計算模型，得到了以下結論：

1）NES 非線性剛度kN、阻尼cN存在著最優參數，適當的質量比μ就可以顯著提升NES 的性能。

2）在設備受到沖擊波作用后的0～100 ms 內，即使在最優參數范圍內，NES 對設備抗沖擊性能的改善作用有限；在沖擊后500 ms 內，NES 顯著降低了設備的沖擊能量，抗沖擊效果好。

3）本文研究的內容，可對艦船隔振裝置沖擊防護提供參考。