基于多項式混沌法的翼型不確定性分析及梯度優化設計

陳藝夫，馬宇航，藍慶生，孫衛平，史亞云，楊體浩，*，白俊強

1．西北工業大學 航空學院，西安 710072

2．中國空氣動力研究與發展中心 計算空氣動力研究所，綿陽 621000

3．中航通飛華南飛機工業有限公司，珠海 519000

4．西安交通大學 航空學院，西安 710049

所有工程系統的性能都會受到某種程度不確定性的影響。由于受到加工制造或飛行條件及環境等諸多不確定性因素的影響，飛行器的性能容易出現較大變化。傳統的氣動設計屬于確定性設計，有可能導致氣動性能對不確定因素異常敏感，甚至會帶來一定的安全隱患。因此，在飛行器設計階段，關注不確定因素對飛行器性能的影響顯得尤為重要。

美國NASA 于1998年對工程上多學科設計領域的需求進行了調查［1］，調查結果表明，需要提高飛機在多種不確定性因素下的不確定性能。2002年，NASA 又推出了有關航空航天領域不確定性下多學科優化設計的規劃［2］，規劃中明確指出了飛行器不確定性下設計的難點和挑戰，為未來一段時間內的研究奠定了基礎。規劃推出后，NASA 蘭利研究中心致力于對跨聲速翼型進行不確定性優化設計。從Huyse［3］和Walters［4］等對二維翼型考慮馬赫數不確定性的優化設計研究中，可以看出確定性優化和不確定性優化之間存在較大差異，進一步說明了在翼型設計中考慮不確定性影響的重要性。

為開展考慮不確定性的魯棒優化設計，首先需要建立高效精確的不確定性分析方法。在不確定性分析中，很重要的一步是將不確定源的特征轉化為輸出變量（Quantity of Interest，QoI）不確定性估計的過程，稱之為不確定性的傳播。不確定性傳播方法可分為4 大類：解析法［5］、取樣法［6］、隨機響應面模型法和代理模型法。

現代氣動設計大量依賴于使用CFD 工具來預測所考慮的氣動外形的性能，在減少了昂貴的風洞試驗的同時，效率因此得到顯著提升，設計周期進一步縮短。Pelletier［7］和Luckring［8］等在其研究中闡述了CFD 模擬中不確定性的來源和分類。Walters 等［4］總結了針對CFD 中不確定性的分析方法。Schaefer 等［9］在其最新的綜述類文章中對當前航空航天領域CFD 模擬的不確定性分析方法進行了總結。Roelofs等［10］在其文章中總結了在不確定性條件下所進行的優化設計研究工作，重點關注的是分配和量化這些不確定性的方法和建模方法。研究發現，概率方法仍然是表示不確定性的最流行理論。多項式混沌展開法和隨機配置方法越來越受歡迎，但蒙特卡洛模擬仍被廣泛使用。

近年來，多項式混沌法在CFD 氣動設計不確定性分析中的應用最為廣泛。Knio 等［11］和Najm［12］在其綜述中總結了多項式混沌法在CFD不確定性分析中的發展和應用現狀。國內外學者采用多項式混沌法對CFD 氣動設計中的不確定性問題開展了大量研究工作。基于非嵌入式多項式混沌法，Loeven 等［13］研究了一維活塞問題和二維亞聲速翼型的不確定性問題。Simon［14］和Chassaing［15］等對二維翼型跨聲速下馬赫數和迎角的不確定影響進行研究，敏感性分析表明，不確定參數之間存在很強的非線性耦合。Yamazaki［16］則利用阻力分解方法分析了二維翼型的不確定性量化問題。在Suga 等［17］的研究中，多項式混沌方法被用于二維超聲速雙翼飛機翼型的氣動不確定性量化。Hosder 等［18］分別對膨脹波拐角角度的幾何不確定性和跨聲速三維機翼的馬赫數、迎角不確定性開展了研究。West 等［19］開發了一種多保真多項式混沌法，并將其成功應用于超聲速客機的不確定性分析問題中。

在內流研究中該方法也已得到了廣泛應用。Ghisu［20］、Abraham［21］和Li［22］等利用非嵌入式多項式混沌法研究了燃氣渦輪壓縮機在不確定工作條件下的響應。Liu 等［23］對渦輪葉片在風速不確定下的總體性能進行了討論。di Stefano 等［24］研究了湍流模型閉合系數不確定性對超燃沖壓發動機流場解的影響。Guo 等［25］通過任意多項式混沌的稀疏近似來評估制造可變性對壓縮機葉片氣動性能的影響。Huang等［26］提出了一種結合非嵌入式多項式混沌法和Smolyak 稀疏網格的不確定性量化方法，對轉子葉尖的氣動和傳熱性能不確定性進行量化。

國內方面，王曉東等采用嵌入式多項式混沌方法分別研究了Burgers 方程的隨機響應［27］和隨機方腔流動中不確定性因素的影響［28］。鄔曉敬等［29］采用非嵌入式多項式混沌法對翼型跨聲速隨機氣動特性進行不確定性及全局敏感性分析。另外，對多項式混沌法的改進也在持續進行。Zhao等［30］提出了一種高效且新穎的自適應多保真稀疏多項式混沌耦合Kriging 方法，該方法具有靈活性高，非線性建模能力強的優點。在Schaefer的最新研究［31］中提出了一種空間精確多項式混沌的新統計方法，該方法可以在整個飛行包線或設計空間內插補或外推偶然和認知不確定性。盡管已經有大量學者利用多項式混沌法開展不確定性分析研究，但不確定性分析中所需的計算成本仍然較高，尤其是當不確定性變量維度和多項式階數增大時。

除了以上所述對不確定性進行分析和量化的研究，降低氣動特性對不確定性變量的敏感性也是氣動優化設計領域的一大挑戰，這需要開展基于不確定性下的魯棒優化設計。

大量研究工作已經基于多項式混沌法展開。根據魯棒優化設計中是否使用梯度，可分為 PCE非梯度類魯棒優化設計、PCE 梯度類魯棒優化設計。基于非梯度類優化方法，Zein［32］結合多項式混沌法提出了一種信任區域優化方法，在信任區域上建立代理模型以完成魯棒優化設計。Wang等［33］耦合了非嵌入式多項式混沌法與多目標遺傳算法，并將其應用于壓縮機轉子葉片的魯棒優化設計中。Palar 等［34］將進化算法和非嵌入式多項式混沌法結合，開展了跨聲速翼型的魯棒優化設計，目標為降低不確定性并最大化升阻比。國內方面，鄔曉敬［35］耦合非嵌入式多項式混沌法和Kriging 代理模型發展了自適應魯棒優化設計方法，對二維翼型進行了考慮不確定性的優化設計。

使用梯度優化算法仍然是解決大規模設計變量氣動優化設計問題最有效的途徑之一，對于考慮不確定性的優化設計其收益將更為明顯。Padulo 等［36］提出了一種簡化正交技術，可在不顯著增加計算成本的條件下用于考慮較少設計變量的翼型氣動優化設計中。Shankaran 等［37］提出了一個魯棒優化框架，結合多項式混沌法和伴隨理論來有效地獲得梯度，以實現考慮馬赫數不確定性的魯棒優化設計。Schillings 等［38］基于多項式混沌和梯度算法對二維歐拉流動不確定性下的氣動外形開展魯棒優化設計研究，目標函數定義為均值和方差的組合。Rallabhandi 等［39］使用PCE方法將伴隨導出的梯度與不確定度量化相耦合來同時對音爆進行魯棒優化，同時降低音爆響度的均值和標準差。Boopathy 等［40］提出了一種半嵌入式隨機Galerkin 方法，該方法可以將確定性導數用于伴隨方法，從而產生隨機的Galerkin 伴隨解。Sabater 等［41］通過耦合非嵌入式高斯過程模型和伴隨方程法搭建了魯棒優化設計框架，為了適應更多的不確定性輸入使用了梯度增強型的Kriging 模型，并成功應用于考慮了馬赫數和迎角不確定性的跨聲速二維翼型的優化設計，所提出的方法可以同時減少阻力的平均值和標準差。

結合以上總結和討論，目前基于多項式混沌法的不確定性分析和梯度優化設計相關研究存在的不足為不確定性分析過程中計算成本較高，優化設計并未包含多種設計狀態或輸入不確定性，且對優化結果的分析不足。因此，本文的研究內容為首先利用伴隨方程法求解目標函數對不確定性變量的導數，發展一種梯度增強型多項式混沌法，以降低優化設計中不確定性分析模塊的計算成本，采用亞聲速和跨聲速二維翼型算例對該方法進行驗證，并量化不確定性變量的全局敏感性。其次，建立不確定性分析模塊統計矩梯度求解方法并搭建優化設計系統。最后，對低亞聲速和跨聲速二維翼型進行考慮馬赫數和迎角不確定性的梯度優化設計，并對優化結果進行分析討論。

1 數值模擬方法和伴隨理論

1.1 數值模擬方法

采用有限體積法求解三維可壓縮雷諾平均Navier-Stokes（RANS）方程，其積分形式如式（1）所示。湍流模型使用Spalart-Allmaras（SA）方程模型。

式中：V為控制體的體積邊界；Q為流場守恒變量；FI和FV分別是無黏通量和有黏通量，在直角坐標系下可分解為3 個方向的分量。

空間離散采用基于有限體積法的JST 空間離散方法。時間推進上采用廣義最小殘差（Generalized Minimal Residual，GMRES）方法，該方法作為一種Newton-Krylov 子空間方法的分支，是目前較為先進的線性系統迭代求解方法之一。

1.2 求解器驗證

驗證模型為ONERA-M6 機翼。計算狀態為Ma=0.84，Re=11.72×106，α=3.06°，該狀態具有較為完備的試驗數據［42］。利用商業軟件ICEM 劃分多塊結構O-H 型網格，網格量為158 萬，邊界層第1 層高度為1×10-6。物面和對稱面網格如圖1 所示。

圖1 M6 機翼網格Fig.1 M6 wing mesh

沿機翼展向分別截取20%展長、44%半展長和65%半展長3 個剖面，將求解器的計算結果和實驗數據進行對比，如圖2 所示。圖中，圓形、方形和菱形數據點為實驗數據（Exp），實線為計算得到的截面壓力分布，可以看出計算結果和實驗數據在各個機翼展向截面吻合均較好，說明采用的CFD 求解器滿足優化設計的精度要求。

圖2 M6 機翼計算結果與實驗數據對比Fig.2 Comparison of M6 wing calculation results with experimental data

1.3 伴隨方程

在梯度優化設計中，高效精確地獲得目標函數對設計變量的導數成為關鍵一環。伴隨方程法求解梯度的效率幾乎不受設計變量個數的影響，對于具有高維特性的氣動優化設計問題具有顯著優勢。

給定目標函數J和設計變量X。計算網格是設計變量的函數G(X)。對于RANS 方程，流場解是計算網格和設計變量的函數Q(G(X)，X)。

目標函數通過對收斂的流場解Q進行積分得到，有

對于收斂的流場解殘差R為0，即

當給定流場解Q時，根據鏈式求導法則得到目標函數對設計變量的Jacobian矩陣：

為了避免求解計算最為耗時的dQ/dX一項，引入伴隨方程：

式中：ψ為伴隨向量。可表示為

從伴隨方程的組成上看，求解伴隨方程并不依賴于設計變量。盡管氣動優化問題具有明顯的高維特性，然而求解伴隨方程需要的時間與單次CFD計算所需的時間大體相當，大大提升了計算目標函數對設計變量梯度的效率。通過求解伴隨方程，可以得到伴隨向量，將式（6）代入式（4）中得到：

式中：?J/?G的計算使用收斂的流場解，對網格變量求一次偏導數即可；dG/dX可根據參數化方法和網格變形算法計算得到。

1.4 梯度驗證

使用有限差分法對伴隨方程求解所得梯度進行驗證。為保證梯度驗證的普適性，隨機挑選某翼型進行梯度驗證，如圖3 所示，在翼型四周布置FFD 控制框。FFD 控制框弦向共12 個控制點，控制點移動方向為y向。在翼型前后緣施加FFD 控制點的移動約束，上下表面FFD 控制點在y方向的移動大小相等，方向相反，以保證前后緣位置不變。由此總的設計變量個數為10×2+2（翼型前后緣設計變量）=22。

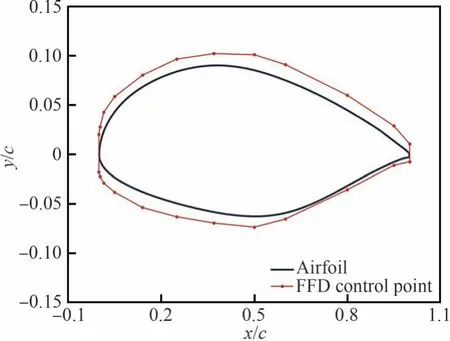
圖3 梯度驗證翼型幾何和FFD 控制框Fig.3 Airfoil geometry and FFD control frame for gradient validation

該翼型計算狀態為Ma=0.69，α=-0.39°，Re=11.7×106，對應于Honda 飛機巡航狀態［43］。表1 和表2 分別展示了針對目標函數CL和CD利用有限差分方法和耦合伴隨方程計算得到的導數值。從對比結果上看，伴隨方程法求解得到的梯度與有限差分法吻合較好，相對誤差在10-3以下，符合有限差分截斷誤差精度。

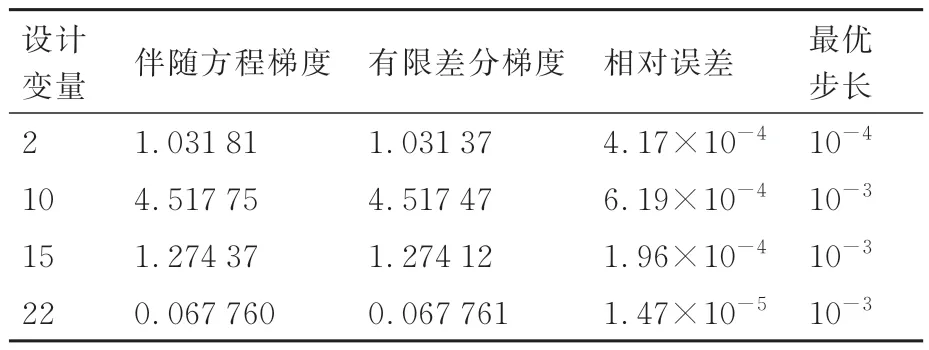
表1 升力系數關于設計變量的梯度驗證Table 1 Gradient verification of lift coefficients with respect to design variables

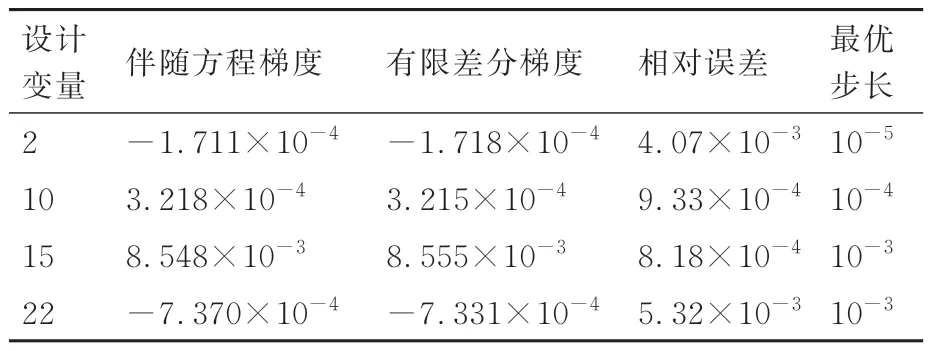
表2 阻力系數關于設計變量的梯度驗證Table 2 Gradient verification of drag coefficients with respect to design variables

2 不確定性分析方法

2.1 多項式混沌法原理

考慮一個可由確定性映射表示的物理模型系統Q=M(X)，這里X=[X1，X2，…，XN]T，N≥1 是輸入變量向量（包括幾何設計變量和來流條件變量等）。Q=[Q1，Q2，…，QM]T，M≥1 是系統提供的一組輸出變量向量。

由于假設輸入向量X中部分n個變量受不確定性影響，因此這一部分的變量可由具有指定概率密度函數（Probability Density Function， PDF）的隨機向量x表示。另一部分的輸入變量為確定性變量，用D表示。這里x為真實隨機變量，其可看作標準隨機變量ξ的函數：

式中：μ和σ分別是該隨機變量的均值和方差。通過不確定性傳播，導致該系統的輸出響應Q也是隨機變量。

多項式混沌法（Polynomial Chaos Expansion， PCE）的核心思想是通過含有獨立隨機變量的正交多項式基尋找隨機變量ξ（輸入參數）與感興趣量Q（QoI）之間的函數依賴關系。將隨機函數Q分解成確定和隨機兩部分，得到式（9）所示的無窮級數表達形式：

在實際使用中，取前P階有限模態截斷，如式（10）所示。在氣動優化設計中D為確定性設計變量向量，ξ為隨機設計變量向量（如迎角、馬赫數、來流湍流度等）。那么αj(D)為該多項式混沌展開第j階的確定性部分，而Ψj(ξ)則為該多項式混沌展開第j階的隨機部分。

采樣總數Ns為P+1，由3 個參數確定：隨機變量的數量p，獨立基函數多項式的階數p和過采樣率np，如式（11）所示。

經過文獻中的研究，過采樣率一般為2，即可在滿足多項式混沌法精度的情況下，最大限度地減少采樣點的個數。

多項式混沌法的關鍵在于求解正交多項式的權重系數αj(D)，采用點配置回歸法進行求解。回歸方法即采用最小二乘方法求解通過確定性抽樣構建的線性方程組。

在隨機空間中選擇Ns個樣本，并在這些點評估確定性問題。最后，針對隨機變量的頻譜模式，建立了一個由Ns個方程組成的線性系統并求解。該線性系統由式（12）給出：

式中：矩陣中的ξ0代表該標準隨機變量矢量ξ在第一個采樣點處的值，同理ξNs-1為標準隨機變量矢量ξ在第Ns個采樣點處的值。最終待求系數矩陣寫成緊致格式為

多項式混沌法的最大優點是可解析表達輸出隨機變量的均值和方差。根據對均值（數學期望）和方差的統計定義，由多項式混沌法得到的輸出隨機變量的均值和方差可表示為式（14）和式（15）：

2.2 梯度增強型多項式混沌法

多項式混沌法的精度和基函數的階數有關，為提高精度需要增加基函數的階數。由式（11）可知階數的增加會導致采樣點數的成倍增加，即需要調用成倍數量的CFD 數值模擬，需要大量的計算資源。

考慮到多項式混沌法精度和采樣點數的矛盾，采用伴隨方程法獲取梯度信息，進而對多項式混沌法進行增強。梯度增強型多項式混沌法（Gradient-enhanced Polynomial Chaos Expansion， GPCE）可以在保證不增加基函數階數的情況下顯著提高多項式混沌法的精度。簡而言之，梯度增強型多項式混沌法可在保證相同的模擬精度下，大幅減少采樣點的個數。

使用這種梯度增強型多項式混沌法，可以構建基于二階回歸的全局敏感性分析，其成本僅隨著維度的增加而線性增加。因此，這種方法甚至可以應用于大維數問題。

梯度增強型多項式混沌法可通過對式（10）所示的PCE 核心公式微分得到。等式的左右兩邊同時對歸一化的標準隨機變量求導數可以得到：

式（16）展開寫成矩陣形式，如式（17）所示：

對于Ns個樣本ξ0，ξ1，…，ξNs-1，n個標準隨機變量ξi，ξi+1，…，ξn，n個真實隨機變量xi，xi+1，…，xn，左端項P+1 個多元聯合基函數Ψj分別對n個歸一化標準隨機變量ξi求導數?Ψj/?ξi。

式（17）右端項中?Q/?x為在每個確定性采樣點處感興趣的輸出變量Q對n個真實隨機輸入變量的確定性梯度，其可以由伴隨方程法直接得到。

由于真實隨機變量x又是標準隨機變量ξ的函數，那么?xj/?ξj可以基于不確定性變量的已知分布獲得。例如，一個均值為μ和標準差為σ的正態分布，單位化形式為

該導數為

如圖4 所示，通過在式（10）左右兩端增加梯度信息對線性系統進行增廣處理。最終得到的基函數梯度增廣矩陣（17）大小為Ns(n+1)×Nb，右端項輸出矩陣大小為Ns(n+1)×Nq，PCE 待求系數矩陣的大小不變，仍然為Nb×Nq。采用梯度增強型PCE，需要的采樣點數仍為Ns，相比于同等精度的PCE 可減少nNs個采樣點。換言之，利用Ns個樣本點可構建與Ns(n+1)個樣本點具有相同精度的多項式混沌響應面。

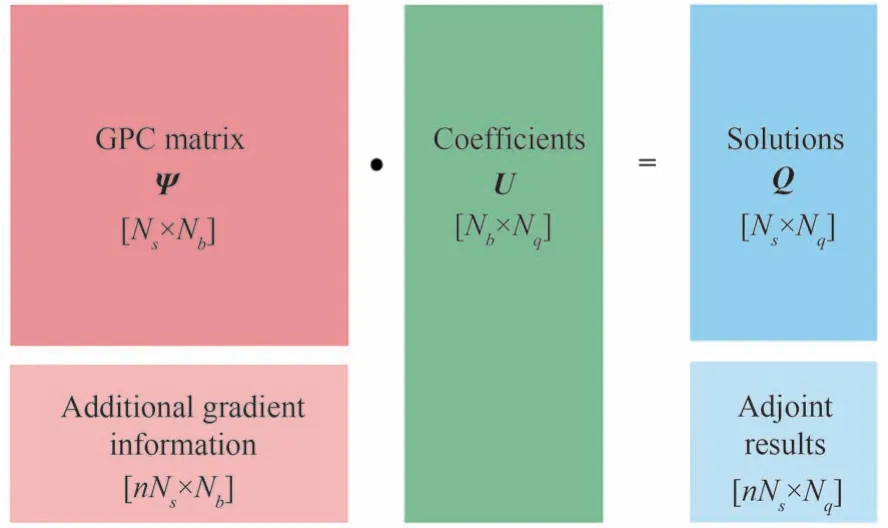
圖4 梯度增強型多項式混沌法Fig.4 Gradient-enhanced polynomial chaos expansion method

2.3 基于方差分解的全局敏感性分析方法

通過不確定性分析，可以得到不確定性因素對輸出的影響，但是要確認每一個不確定性變量對這一影響的貢獻程度，還需要進行敏感性分析。敏感性分析分為全局敏感性分析和局部敏感性分析。全局敏感性分析可以克服局部敏感性分析的局限性，不僅考慮了各因素概率密度函數的分布和形態的影響，而且在分析時所有因素可同時變化，還可以不受模型限制并考察輸入參數在整個參數變化范圍內對輸出的貢獻程度。本文采用基于方差分解的全局敏感性分析方法。

由方差降維分析，總方差可以表示為

式中：

方差分解顯示了如何將模型輸出的方差分解為可歸因于每個輸入的項，以及它們之間的交互作用。所有項加在一起就是模型輸出的總方差。根據以上的數學推導，定義一種基于直接方差分解的敏感性度量Sobol 指數，如式（22）所示。

式中：Si稱為“一階敏感性指標”或“主效應指標”，其反映的是Xi對輸出方差的貢獻，由總方差進行歸一化。同理，可以通過將方差分解中的其他項除以Var(Q) 來形成高階交互的Sobol 指數Sij，Sijk等：

基于多項式混沌法的Sobol 指數可以方便地表示為式（24）和式（25），詳細推導見文獻［44］。

2.4 統計矩梯度求解

基于梯度的不確定性優化設計需要求解不確定性分析模塊的梯度信息，即包括隨機輸出變量均值對設計變量的梯度dμQ/dD和標準差對設計變量的梯度dσQ/dD。

由PCE 方法可知，隨機輸出變量Q的均值和方差可以解析地表達為式（14）和式（15）。將均值對設計變量進行微分，得到式（26）。

式中：dQ/dD是每個確定性采樣點處輸出變量Q對設計變量的梯度，該項由伴隨方程法直接獲得。那么該式可以簡單地理解為輸出變量均值對設計變量的梯度等于輸出變量對設計變量梯度的均值。

輸出變量方差對設計變量的梯度可以表示為

為了求式（27）的梯度值，需要確定多項式系數對設計變量的梯度dαj/dD。對于第個設計變量，可以通過對PCE 核心公式微分來構造第二個多項式混沌展開。式（10）的多項式混沌法核心公式左右兩端同時對設計變量求導可得

式中：左端項?Y(D，ξ)/?Dj可由伴隨方法求得；右端項中Ψi(ξ)為在構建PCE 時選定的多項式基函數，那么待求項只剩這個新構造的多項式展開的新系數dαi(D)/dDj，同樣可利用回歸方法求解。

對于nDV個設計變量，需要構建nDV個線性系統，如式（29）所示：

通過求解這nDV個線性系統，可得到輸出變量Q對nDV個設計變量的導數dQ/dD。

3 優化設計框架

3.1 優化設計輔助技術

采用FFD 參數化方法。FFD 參數化方法基于彈性體變形思想來表示幾何變形問題。其核心公式為

式中：Xs為設計外形上任意一點的全局坐標向量，(u，v，w)為其參數坐標向量，u，v，w的取值范圍為(0，1)；Pi，j，k是控制框中每個控制點的全局坐標向量。

選擇逆距離權重插值算法（Inverse Distance Weighting， IDW）作為本文的網格變形算法，以建立網格變形方法的實質是建立空間網格與表面網格的映射關系。IDW 算法的核心公式為

式中：N是選為插值基點的個數；u(xv)為空間網格待插值點；uj為表面網格插值基點；wj為第j個位置的權重系數，與空間網格插值點到表面網格插值基點的距離成反比。

經大量實踐發現，序列二次規劃算法是目前針對高維度大規模設計變量光滑非線性規劃問題表現最優的算法之一。本文使用基于序列二次規劃算法的SNOPT 作為優化算法。

3.2 確定性優化設計框架

結合3.1 節介紹的優化設計輔助技術，可最終搭建如圖5 所示的確定性優化設計系統。具體優化步驟如下：

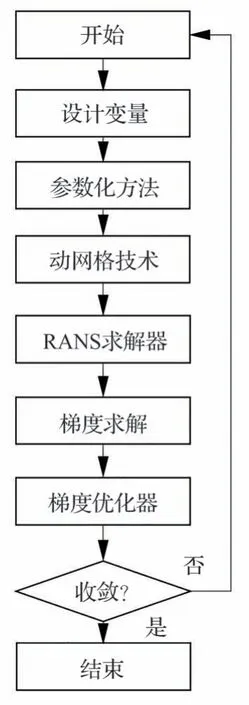
圖5 確定性優化設計框架Fig.5 Deterministic optimization design frame

1）建立初始模型和網格，給定設計變量的初值X0。

2）通過FFD 方法對表面網格xs進行參數化變形。

3）基于第2）步變形后的表面網格，通過IDW 動網格技術得到變形后的空間網格xv。

4）求解器求解RANS 方程，計算流場結果Q。

5）基于流場結果，計算伴隨方程并求解目標函數對設計變量的梯度信息dJ/dX。

6）結合第4）步中流場計算結果和第5）步中的梯度信息，使用SNOPT 優化算法對設計變量進行更新。

7）重復第2）步～第6）步，直至優化設計收斂。

3.3 不確定性優化設計框架

考慮不確定性后，修改目標函數為輸出變量的 均 值 和 方 差 的 線 性 組 合J=K1×μq+K2×σq，優化設計系統中需引入多項式混沌法分析模塊來計算不確定性的傳播過程，并得到輸出變量的均值和方差及兩者對設計變量的梯度信息。最終可搭建如圖6 所示的不確定性優化設計系統。具體優化步驟如下：

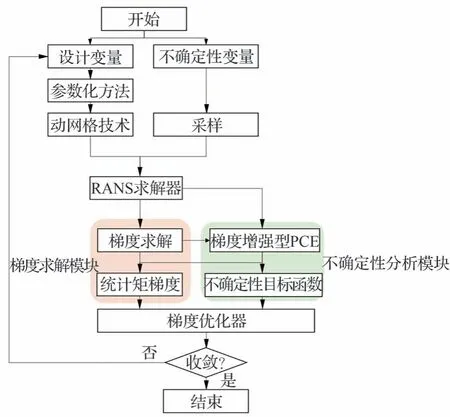
圖6 不確定性優化設計框架Fig.6 Uncertain optimization design frame

1）建立初始模型和網格，給定設計變量的初值X0。

2）通過FFD 方法對表面網格xs進行參數化變形。

3）基于第2）步變形后的表面網格，通過IDW 動網格技術得到變形后的空間網格xv。

4）設定不確定性變量，例如馬赫數M或迎角α等。根據不確定性變量在隨機空間進行采樣，采樣數為Ns。

5）求解器在每個采樣點進行確定性分析，求解RANS 方程，計算流場結果Q。

6）基于流場結果，在每個采樣點進行確定性分析計算伴隨方程，得到不確定性輸出變量q對設計變量的導數dq/dX。

7）基于確定性分析結果，構建梯度增強型多項式混沌線性方程組ΨC=Q，求解系數矩陣C，得到輸出變量的均值μq和方差σq。

8）利用確定性分析所得梯度耦合多項式混沌系統的梯度，求解輸出變量均值及方差對設計變量的導數dμq/dX，dσq/dX。那么目標函數的梯度可由兩者進行線性表示：

9）根據第8）步中的梯度信息，使用SNOPT優化算法對設計變量進行更新。

10）重復第2）步～第9）步，直至優化設計收斂。

4 考慮飛行條件不確定性的翼型不確定性分析

本節將以亞聲速及跨聲速翼型算例進行不確定性分析，同時可驗證梯度增強型多項式混沌法的計算精度。

4.1 亞聲速翼型

選擇NACA0012 翼型進行亞聲速狀態全湍流下多項式混沌法不確定性分析的精度測試。假設馬赫數滿足Ma～N(0.5，(0.02)2)的正態分布，迎角滿足α～N(1.5，(0.2)2)的正態分布。

計算高度為10 km，計算網格如圖7 所示，采用全湍流計算。為驗證多項式混沌法的精度，分別進行5 000、10 000 次蒙特卡洛法作為驗證標準。蒙特卡洛法在采樣點總數足夠多時，其所得結果趨近于真實值。計算結果如表3 所示。2 次采樣的結果在均值上基本一致，方差上有較小的不同，數值上基本收斂，因此可作為驗證多項式混沌法的標準。

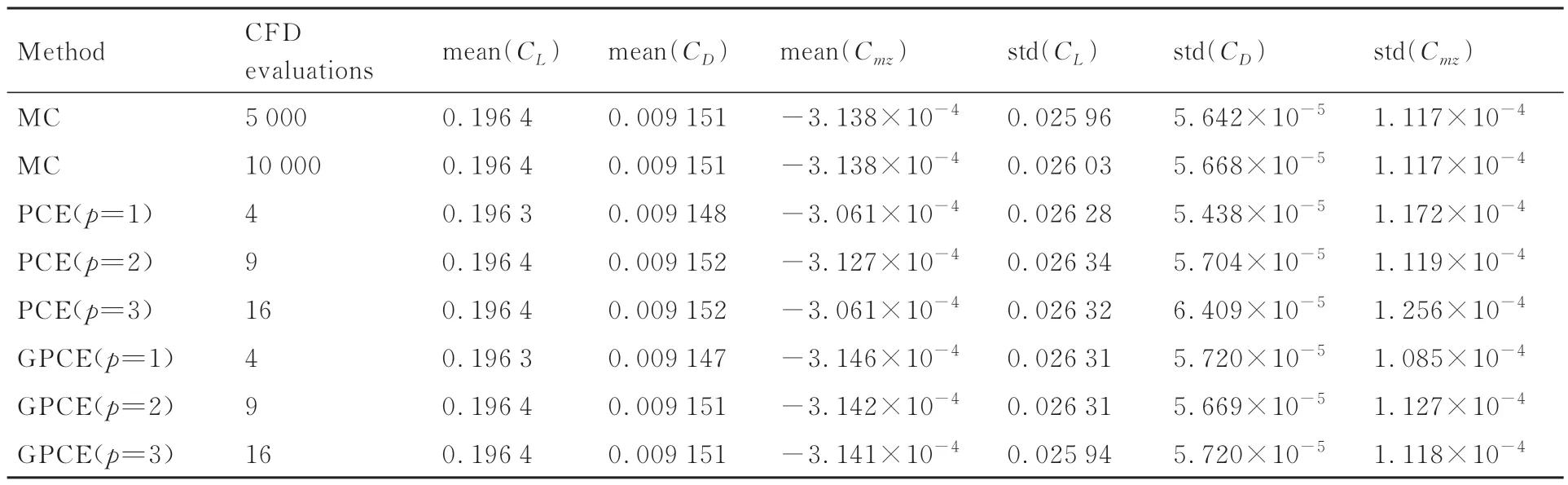
表3 亞聲速翼型：蒙特卡洛法和PCE 法計算結果Table 3 Subsonic airfoil： Monte Carlo and PCE calculation results

圖7 NACA0012 網格Fig.7 NACA0012 mesh

為檢驗PCE 方法的精度，定義PCE 方法的相對誤差為

式中：J=mean(CL)，mean(CD)，mean(Cmz)，std(CL)，std(CD)，std(Cmz)。

使用1～4 階的獨立基函數多項式，采樣點數從10～70 個不等，分別采用傳統PCE 方法和梯度增強型PCE 方法得到誤差在階數和采樣點數空間內的分布，如圖8 所示。圖中顯示的是3 個力系數均值和方差的相對誤差總和，即

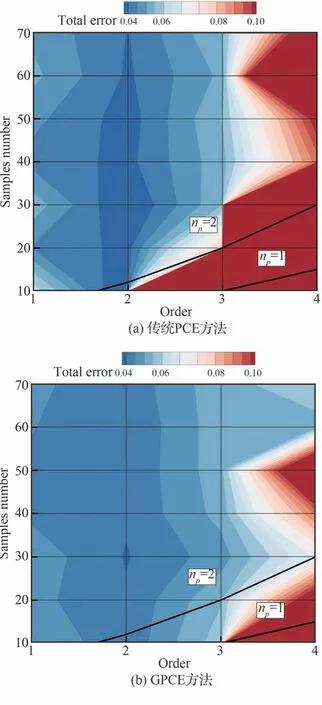
圖8 亞聲速翼型：傳統PCE 和梯度增強型PCE 的精度對比Fig.8 Subsonic airfoils： Accuracy comparison of conventional PCE and gradient-enhanced PCE

從表3 中可以看出和蒙特卡洛法的結果對比，GPCE 方法在預測力系數標準差的精度上具有明顯優勢。同時，梯度信息的引入對低階多項式混沌法的精度增強效果較弱，但能在一定程度上減輕高階多項式混沌法的過擬合現象，從而提高精度。這一點從圖8 中也能看出，梯度增強型的PCE 方法大幅增加了采用3 階或4 階基函數時多項式混沌法的擬合精度。對于亞聲速全湍流狀態，采用1 階或2 階的多項式混沌法已經可以滿足預測精度的要求，更高階的基函數不僅會增加采樣點的個數和計算成本，還會導致精度降低。

分別使用蒙特卡洛法和梯度增強型PCE 法計算得到的亞聲速翼型表面平均壓力分布系數沿弦向的分布如圖9 所示。圖中實線表示在不確定輸入的影響下壓力系數的均值，陰影部分表示壓力系數均值上下正負3 倍標準差區間。從圖中可以看出，受輸入不確定性影響最大的是翼型頭部，梯度增強型PCE 法模擬的均值和標準差與蒙特卡洛法幾乎完全重合，具有較高的精度。

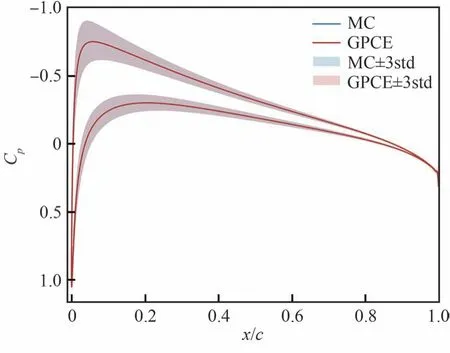
圖9 亞聲速：表面壓力系數不確定性響應對比Fig.9 Subsonic： Comparison of surface pressure coefficient uncertainty response

圖10 和圖11 分別展示了蒙特卡洛法和梯度增強型多項式混沌法計算得到的流場平均壓力系數分布和壓力系數在流場中的標準差云圖。從標準差云圖上看，NACA0012 翼型在給定的馬赫數和迎角輸入不確定性條件下，空間流場的不確定性主要集中在翼型的前50%弦長，尤其是上表面的負壓峰處，受不確定性影響最為顯著。對比蒙特卡洛法得到的流場結果和多項式混沌法得到的流場結果，兩者高度相似。

圖10 亞聲速翼型：2 種方法流場壓力系數均值對比Fig.10 Subsonic airfoils： comparison of mean values of flow field pressure coefficients between two methods Subsonic airfoils

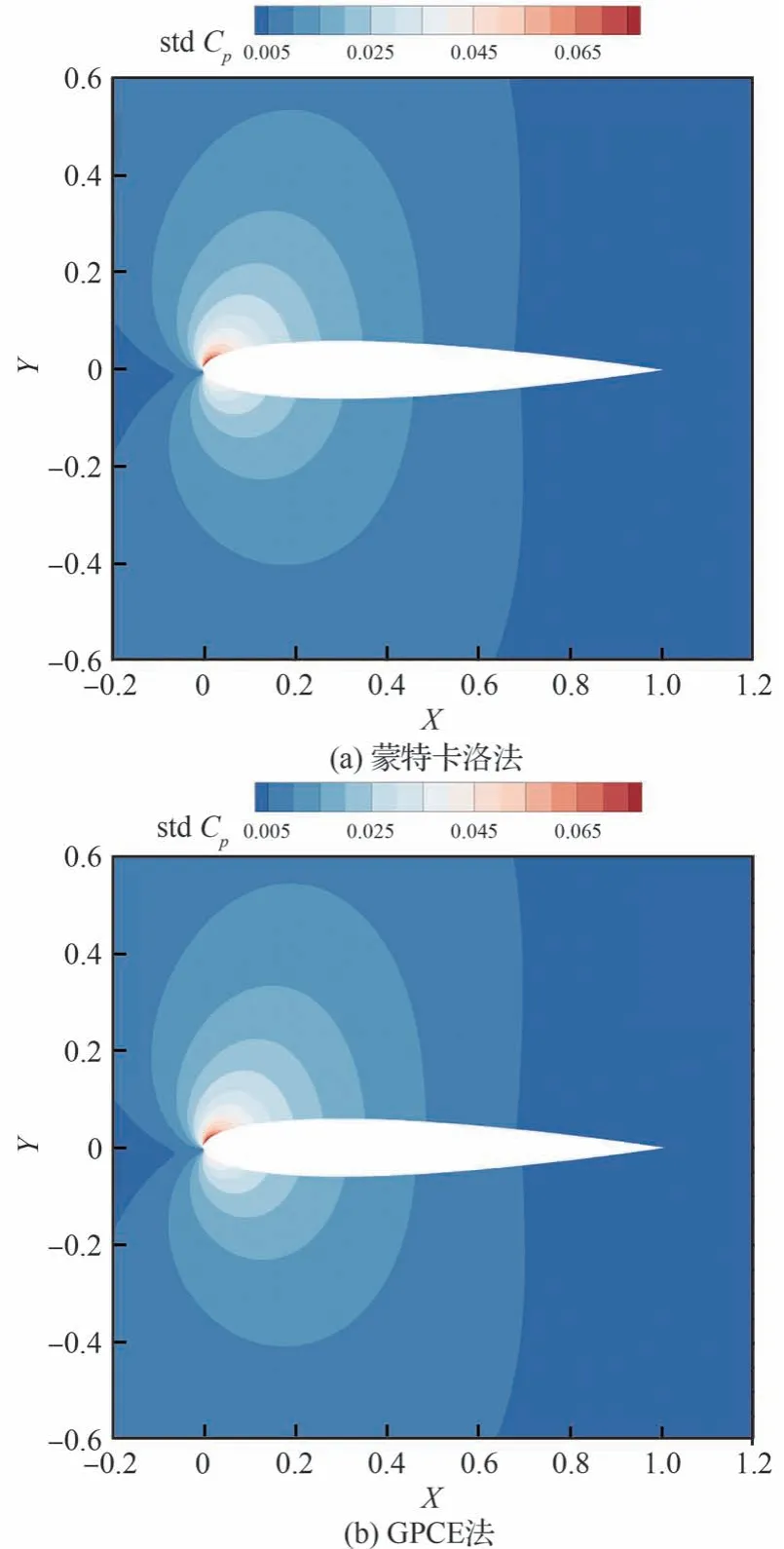
圖11 亞聲速翼型：2 種方法流場壓力系數標準差對比Fig.11 Subsonic airfoils： Comparison of standard deviation of flow field pressure coefficient between two methods

圖12 所示為翼型表面歸一化Sobol 指數沿弦向的分布。圖中［-1，0］為下表面，［0，1］為上表面。Sobol指數在上下表面近似呈對稱分布，在上下表面前90%弦長范圍內都由迎角的不確定性主導，而在前后緣的10%范圍內受馬赫數不確定性影響較大。2個不確定性參數之間基本不存在耦合效應。

圖12 亞聲速表面 Sobol 指數弦向變化Fig.12 Subsonic surface Sobol exponent chordwise variation

受馬赫數和迎角2 種不確定性影響的翼型空間流場歸一化Sobol 指數云圖如圖13 和圖14 所示。圖中顯示出在亞聲速全湍流狀態下，馬赫數不確定性主要影響翼型頭部和尾部的流場方差，而其他空間流域內的不確定性主要由迎角的不確定性支配。兩種不確定性因素之間的耦合作用較小。

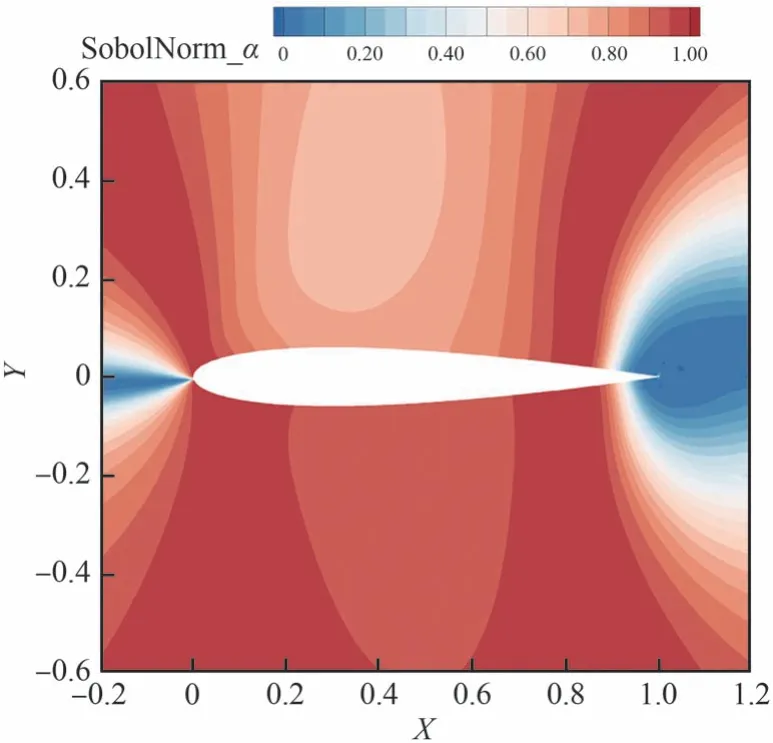
圖13 亞聲速Sobol 指數：迎角Fig.13 Subsonic sobol index： Angle of attack

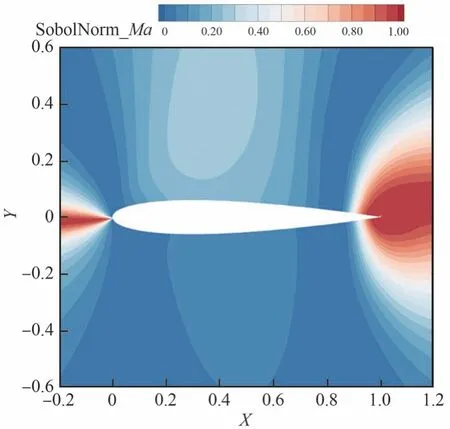
圖14 亞聲速Sobol 指數：馬赫數Fig.14 Subsonic sobol index： Mach number

4.2 跨聲速翼型

選擇RAE2822 翼型進行跨聲速狀態全湍流下多項式混沌法不確定性的精度測試，并對該狀態進行不確定性分析和全局敏感性分析。

計算網格如圖15 所示，弦向布置281 個網格點，法向121 個網格點，附面層第1 層高度1×10-6。計算狀態為Re= 6.5×106，馬赫數滿足Ma～N(0.734，(0.02)2)的正態分布，迎角滿足α～N(2.79，(0.2)2)。選取的狀態流場中具有強激波，呈現高度非線性效應，對驗證工作有益［45］。分別進行了5 000、10 000 次蒙特卡洛分析，得到力系數的計算結果如表4 所示。表中顯示5 000、10 000 次蒙特卡洛法的結果，2 次結果較為接近，可認為蒙特卡洛法收斂，將其作為檢驗多項式混沌法精度的標準。

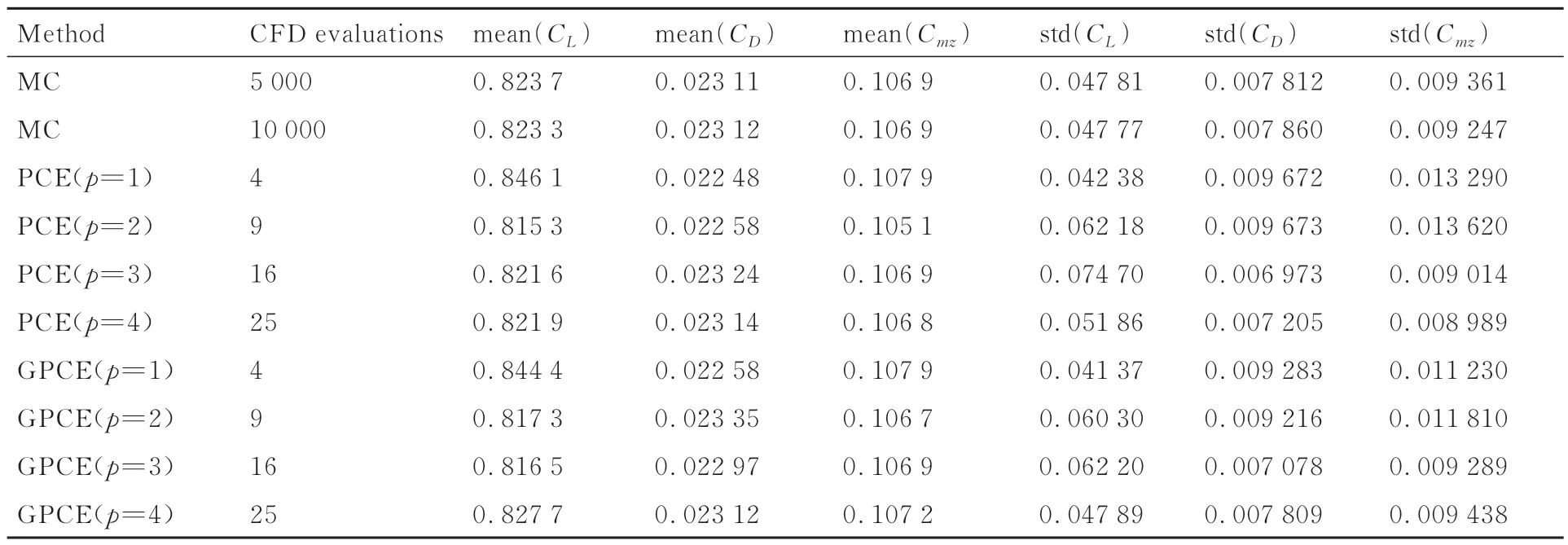
表4 跨聲速翼型：蒙特卡洛法和PCE 法計算結果Table 4 Transonic airfoils： Monte Carlo and PCE calculation results

圖15 RAE2822 翼型計算網格Fig.15 RAE2822 airfoil mesh

分別使用1～4 階傳統PCE 方法和梯度增強型PCE 方法進行該問題的不確定性傳播，結果如表4 所示。在跨聲速條件下，流場非線性效應大幅增加，從而增加了PCE 方法的預測難度。從表中可以看出，傳統PCE 方法和蒙特卡洛法在各個力系數均值的結果上差異較小，而在力系數標準差的預測上兩者誤差有所增大。梯度增強型PCE 方法的模擬精度較傳統PCE 方法具有一定提升，其主要體現在對力系數標準差的預測上，例如對比PCE（p=4）和GPCE（p=4）。

同樣，利用亞聲速下的精度驗證方法，即式（33），選取采樣點數從6～50 個不等，分別采用傳統PCE 方法和GPCE 方法得到誤差在階數和采樣點數空間內的分布，如圖16 所示。圖中顯示，在跨聲速狀態下GPCE 方法仍能在一定程度上減輕高階多項式混沌法的過擬合現象，例如4階和5 階。盡管GPCE 方法相比于傳統PCE 方法的優勢在跨聲速狀態下整體上有所減弱，然而需要注意到其重點改善了低階、小樣本數情況下的擬合精度，這對于減少計算成本是有利的。

圖16 跨聲速翼型：傳統PCE 和梯度增強型PCE 的精度對比Fig.16 Transonic airfoils： Accuracy comparison of conventional PCE and gradient-enhanced PCE

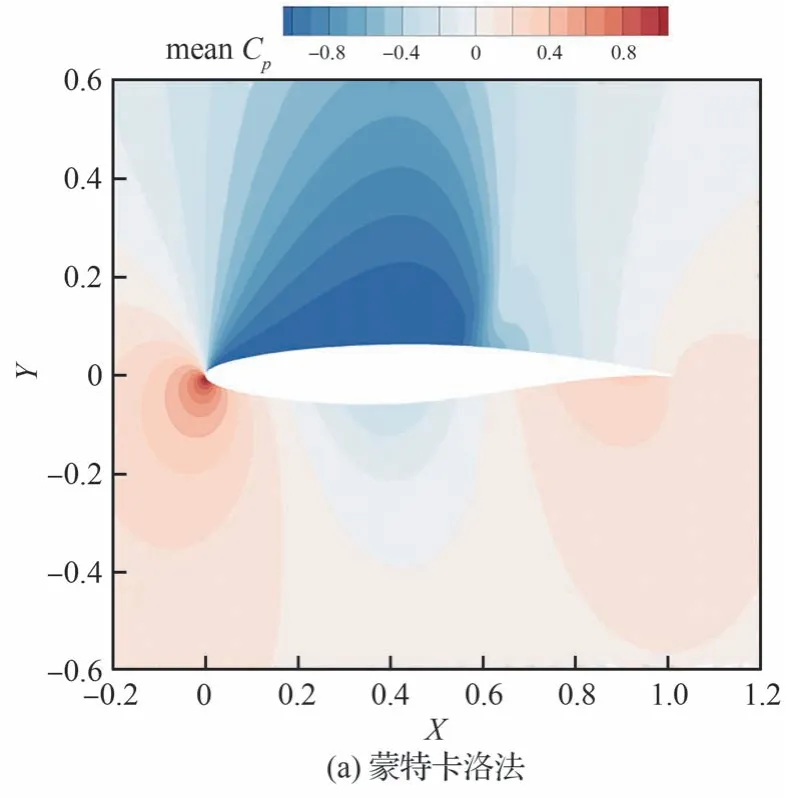
使用蒙特卡洛法和GPCE 法計算得到的流場中壓力系數均值和標準差云圖如圖17 和圖18所示。對比2 種方法的結果可以看到，GPCE 法能夠較為精確地模擬不確定性在跨聲速流場中的傳播，包括流場中具有較強非線性的激波區域。從壓力分布均值上看，在該狀態下翼型上表面 60%弦長處存在一道強激波。相應的，標準差云圖中顯示出該位置受不確定性影響最明顯，標準差最大。

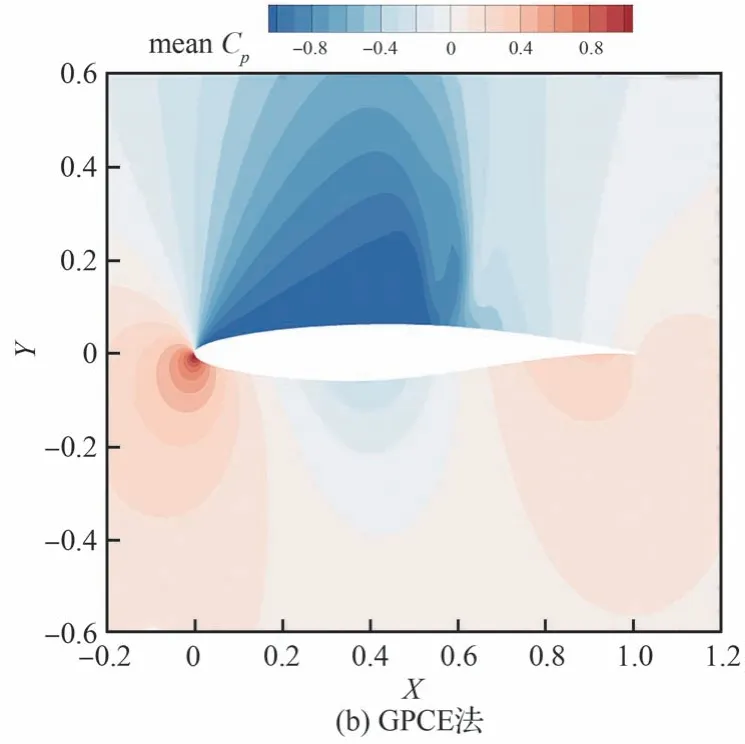
圖17 跨聲速翼型：2 種方法壓力系數均值對比Fig.17 Transonic airfoils： Comparison of mean values of flow field pressure coefficients between two methods

圖19 所示為翼型表面 Sobol 指數沿弦向的分布，在跨聲速狀態下，占主導地位的是馬赫數，在激波位置附近馬赫數、迎角及其耦合作用存在競爭。

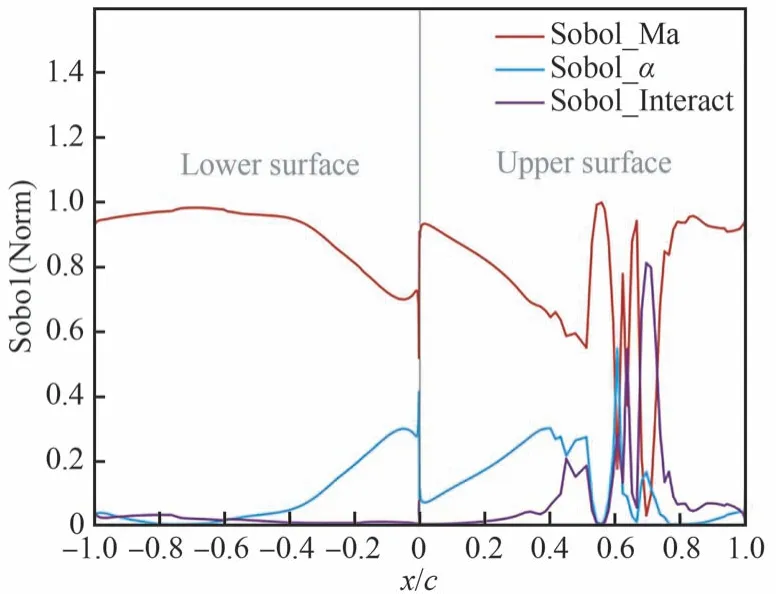
圖19 跨聲速表面 Sobol 指數弦向變化Fig.19 Transonic surface Sobol exponent chordwise variation

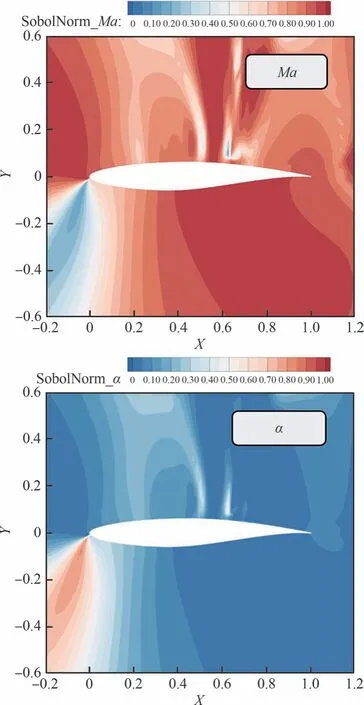
通過梯度增強型多項式混沌法求解的歸一化Sobol 指數云圖如圖20 所示。從圖中可以看出，在跨聲速全湍流流場中，馬赫數不確定性占主導地位，其影響流場中的大部分區域，尤其是激波位置處，但對下表面前緣區域影響較小，由于本例為正迎角工況，因此該處主要受迎角不確定性的影響。馬赫數和迎角的交互作用主要集中在翼型上表面激波前后區域。

圖20 跨聲速全局敏感性分析結果Fig.20 Transonic global sensitivity analysis results

5 考慮飛行條件不確定性的翼型確定性及不確定性優化設計

5.1 低亞聲速翼型優化設計

初始翼型選擇RAE2822，參考Cessna 狀態，Ma= 0.19，Re= 5×106，CL= 0.3。FFD 控制框如圖21 所示。控制框在翼型頭部加密以更好地控制翼型前緣的型面。定義式（35）所示的確定性和不確定性優化問題。

圖21 翼型優化FFD 控制框Fig.21 Airfoil optimization FFD control frame

優化過程中設計變量總數為16 個，均為幾何設計變量。不確定性優化中假設馬赫數和迎角分別滿足Ma～N(0.19，(0.05)2)的正態分布和α～N(0.45，(1.0)2)的正態分布，此時均值狀態下翼型升力系數為0.3。優化過程中使用3 階梯度增強型多項式混沌法，預測誤差可保持在0.1%左右。

表5 給出了低亞聲速翼型優化的確定性和不確定性力系數結果，其中各確定性的力系數為基準流場結果，即Ma=μ(Ma)，α=μ(α)。確定性優化設計結果命名為DeOpt （Deterministic Optimization）；不確定性優化設計結果命名為UMOpt （Uncertainty Multiple factor Optimization）。從表5 中的確定性力系數可以看到，確定性優化最終減阻10.03 counts，約為10.15%。其中主要減少的是壓差阻力，而摩擦阻力幾乎保持不變。不確定性優化總減阻量為9.33 counts，略小于確定性優化。另一方面，從阻力系數的不確定性統計響應結果上看，不確定性優化無論是均值還是標準差均要小于初始構型和確定性優化結果。相比于初始構型，不確定性優化結果阻力系數均值減少約17%，阻力系數標準差減少約80%。綜合以上兩個方面，可以得出結論：不確定性優化在確定性基準場的性能上有所犧牲，以換取在擾動范圍內性能的魯棒性。

表5 低亞聲速翼型優化結果（阻力系數單位為counts）Table 5 Low subsonic airfoil optimization results （Drag coefficient in counts）

對比確定性和不確定性的結果，如圖22 和圖23 所示。UMOpt 翼型上表面前緣厚度較DeOpt 翼型有所增大，下表面前緣的前加載現象消失，厚度增大在壓力分布上體現為上下表面的順壓梯度相比于DeOpt 翼型增大，吸力峰位置前移。

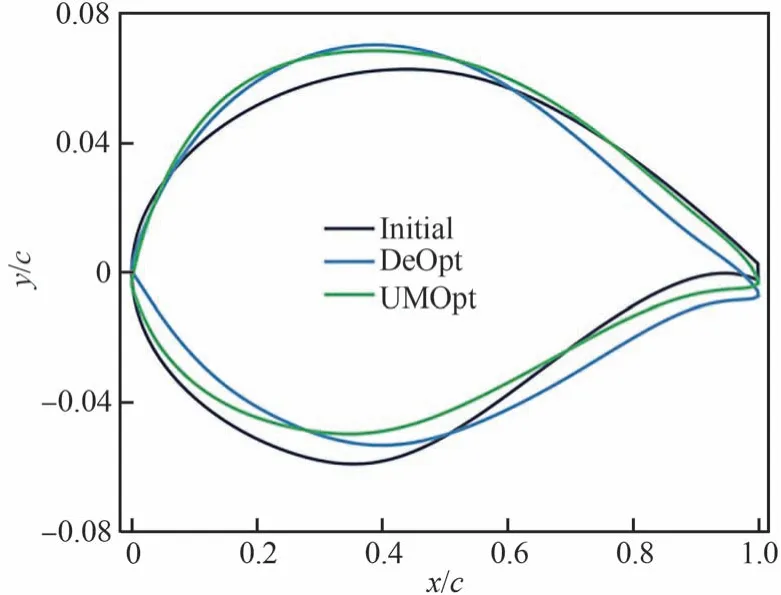
圖22 低亞聲速確定性及不確定性優化翼型對比Fig.22 Comparison of low subsonic deterministic and uncertain optimized airfoils

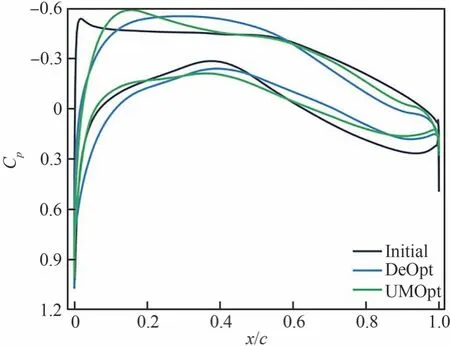
圖23 低亞聲速確定性及不確定性優化壓力分布對比Fig.23 Comparison of low subsonic deterministic and uncertain optimal pressure distributions

采用蒙特卡洛法在隨機空間內采樣并進行確定性分析，得到的隨機樣本點阻力系數分布如圖24 所示。小提琴圖代表樣本點阻力系數的分布特性，圖中越飽滿的部分其概率密度越大，樣本點落在該區間的個數越多。每個小提琴圖中心的黑色粗實線代表上下四分位數的區間，中間點代表整體數據的中位數。因此直觀上看，小提琴圖的上下位置可近似代表阻力系數平均值的高低，越靠下的代表平均阻力系數更低；小提琴圖的形狀代表了阻力性能的魯棒性，越細長的小提琴圖說明阻力系數標準差更大魯棒性更差，越短粗的說明阻力系數標準差更小，性能更加集中，魯棒性更好。對比3 種翼型的小提琴圖結果發現，UMOpt 翼型具有明顯優勢。初始構型無論是平均性能還是性能的魯棒性都較差，DeOpt翼型和UMOpt 翼型均大幅降低了阻力系數的平均值，但相比來講UMOpt 的性能更加向平均值集中。

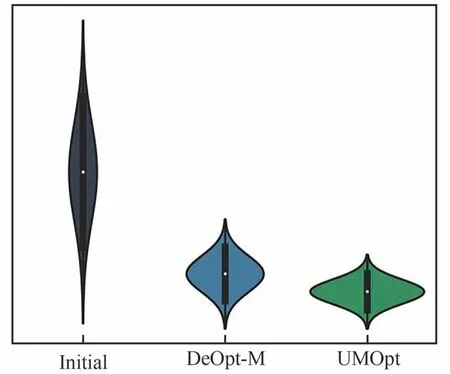
圖24 低亞聲速確定性及不確定性優化阻力系數的隨機分布Fig.24 Random distribution of drag coefficients for low subsonic deterministic and uncertain optimization

將初始構型、DeOpt 翼型、UMOpt 翼型受馬赫數和迎角不確定性影響的空間流場壓力系數標準差云圖進行對比。從圖25 中可以看出在上表面前緣位置處流場壓力系數標準差大小排序為UMOpt＜DeOpt＜Initial。因此，全湍流下考慮不確定性的優化設計相比于確定性優化設計更能有效降低空間流場內壓力系數的不確定性，體現了不確定性優化設計的優勢。

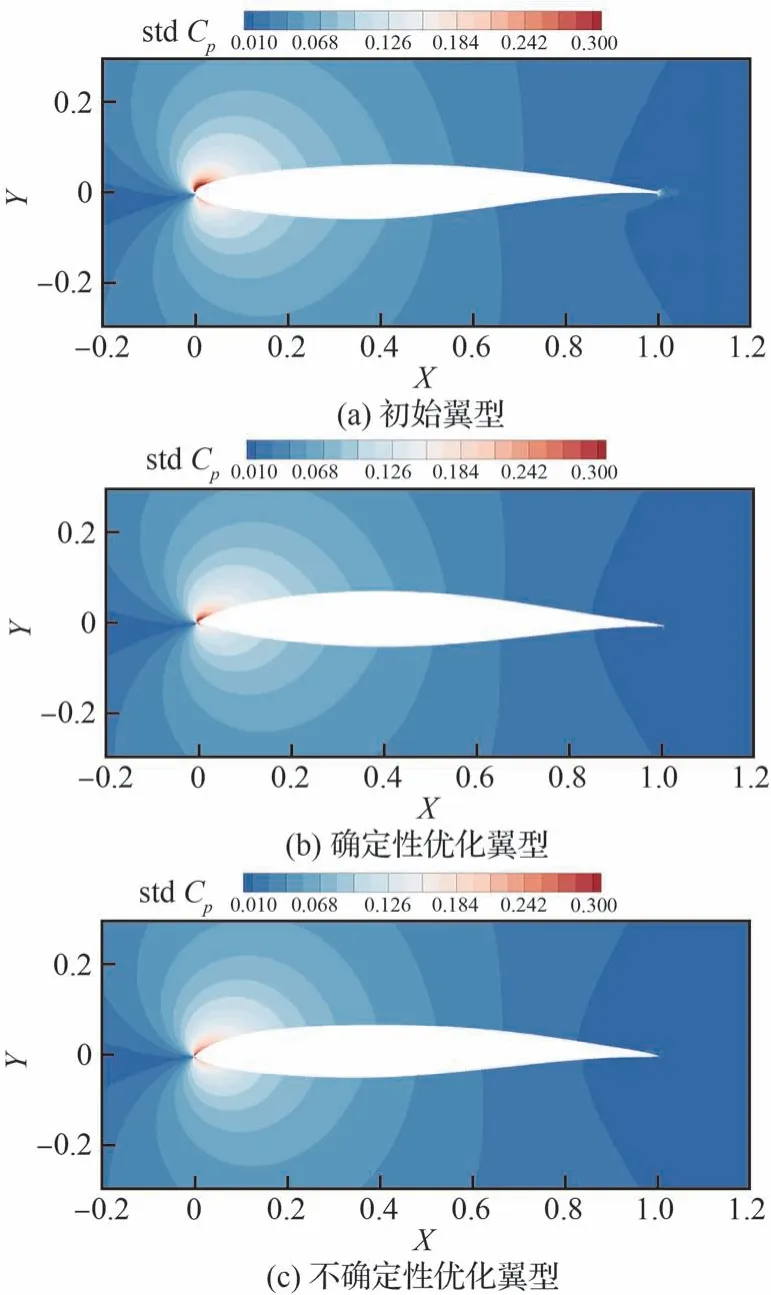
圖25 考慮馬赫數和迎角不確定性下初始、確定性及不確定性優化結果空間流場壓力系數標準差云圖Fig.25 Standard deviation contour of pressure coefficient of initial， deterministic and uncertain optimization results considering uncertainty of Mach number and angle of attack

確定性和不確定性優化歷程如圖26 所示。各個圖中確定性優化歷程以三角形在線中標示，不確定性優化歷程以圓形在線中標示，不確定性優化過程中確定性基準場阻力系數以灰色線表示。由于不確定性優化中的目標函數為J=μ(CD)+σ(CD)，因此灰色圓形標注線和黑色圓形標準線之間的差可近似表示標準差的大小。圖中分別用不同顏色標注了不確定性優化過程中的關鍵節點位置，并在其旁邊展示了壓力分布的均值和標準差響應結果以及翼型的變化。壓力分布圖中每一個關鍵迭代步除了可以和上一關鍵步對比壓力分布均值外，還可以始終與初始翼型對比壓力分布均值和標準差響應范圍。

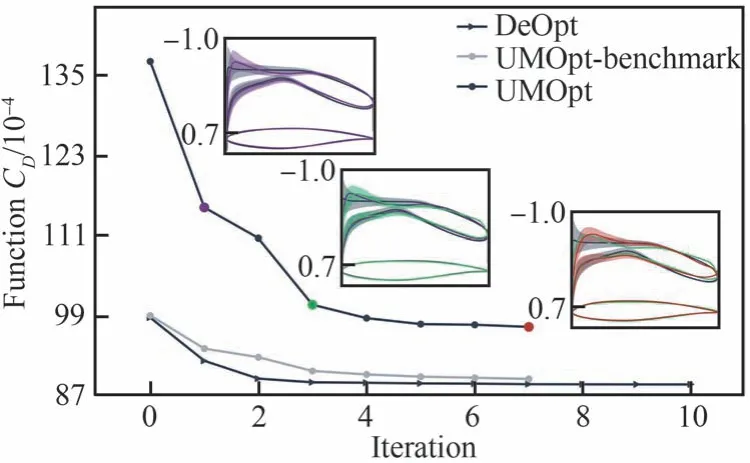
圖26 低亞聲速確定性及不確定性優化歷程（黑色圓形線：DeOpt，確定性優化目標函數變化；黑色三角線：UMOpt，不確定性優化目標函數變化；灰色圓形線：UMOpt，不確定性優化中基準流場的阻力系數變化）Fig.26 Low subsonic deterministic and uncertain optimization history（Black circle line： DeOpt，change of objective function in deterministic optimization； black triangle line： UMOpt，change of objective function in uncertainty optimization； gray circle line： UMOpt， change of drag coefficient of mean flow field in uncertainty optimization）

不確定性優化歷經主迭代8 次，最終滿足約束和目標函數收斂條件。優化過程中前幾步主迭代目標函數下降明顯，而最后幾步目標函數變化較小，主要完成的是對壓力分布的調整和光順，優化過程中阻力系數標準差大幅減小。不確定性優化設計主要的優化方向為小幅提高上表面頭部吸力峰峰值，并不斷推遲吸力峰出現的位置；降低下表面的順壓梯度。優化的最終結果UMOpt 翼型基準場阻力系數略大于DeOpt 翼型，但在翼型頭部附近的標準差響應明顯小于DeOpt 翼型。

5.2 跨聲速翼型優化設計

初始翼型選擇RAE2822，設計狀態參考Honda Jet，Ma= 0.70，Re= 7.93×106，CL=0.38。FFD 控制框與低亞聲速狀態下保持一致，即圖21 所示。對于該翼型分別進行單點確定性優化設計和考慮馬赫數和迎角不確定性的優化設計。定義如式（36）所示的優化問題。相比于低亞聲速優化增加力矩約束以控制低頭力矩。

在考慮馬赫數和迎角不確定性的優化中假設馬赫數和迎角分別滿足Ma～N(0.70，(0.05)2)和α～N(0.387，(1.0)2)的正態分布，此時均值狀態下翼型升力系數為0.38。根據PCE 驗證結果，在跨聲速優化設計中選擇使用3 階梯度增強型多項式混沌法，可將誤差控制在1%以下。

表6 給出了跨聲速翼型優化的確定性和不確定性力系數結果，其中各確定性的力系數為基準流場結果，即Ma=μ(Ma)，α=μ(α)。UMOpt翼型確定性基準場阻力略大于DeOpt 翼型，但從不確定性結果上看UMOpt 翼型的阻力系數均值（89.19 counts）相比于初始翼型減少約6%，略小于DeOpt 翼型的阻力系數均值（91.44 counts）。在阻力系數標準差響應上，差異更加明顯，UMOpt 翼型僅為1.6 counts，與初始翼型相當。而DeOpt 翼型的阻力系數標準差為5.11 counts，甚至高于初始翼型，表明僅考慮確定性性能的優化結果有可能導致性能魯棒性變差。

表6 跨聲速翼型優化結果（阻力系數單位為counts）Table 6 Transonic airfoil optimization results （Drag coefficient in counts）

圖27 和圖28 分別為確定性優化和不確定性優化的翼型結果對比和壓力分布對比。DeOpt翼型頭部半徑變大，上表面最大厚度位置前移，下表面前緣厚度變小。相應的壓力分布上表面吸力峰增大。為了滿足力矩約束，后緣被卸載，原本的后加載被消除，升力載荷向頭部移動。

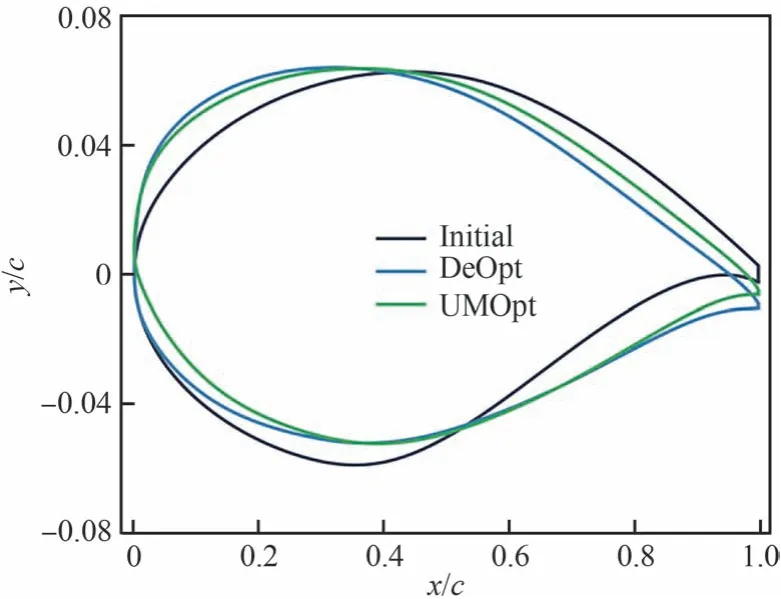
圖27 跨聲速確定性及不確定性優化翼型對比Fig.27 Comparison of transonic deterministic and uncertain optimal airfoils

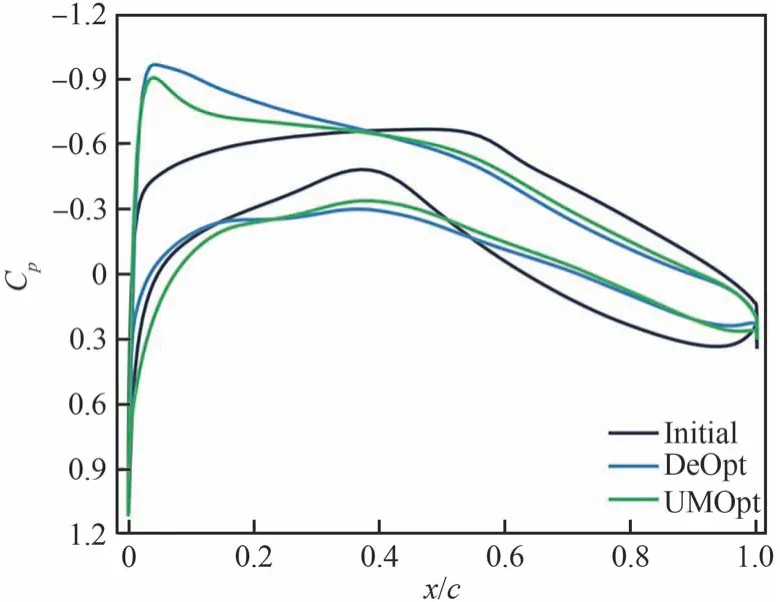
圖28 跨聲速確定性及不確定性優化壓力分布對比Fig.28 Comparison of transonic deterministic and uncertain optimal pressure distribution

從圖29 所示的小提琴圖中可以看出，UMOpt 翼型具有明顯優勢。DeOpt 翼型在馬赫數和迎角的不確定性擾動下具有比初始翼型更差的阻力性能魯棒性。相比之下，UMOpt 翼型在保持初始構型魯棒性基本不變的情況下進一步降低了阻力系數的平均值。

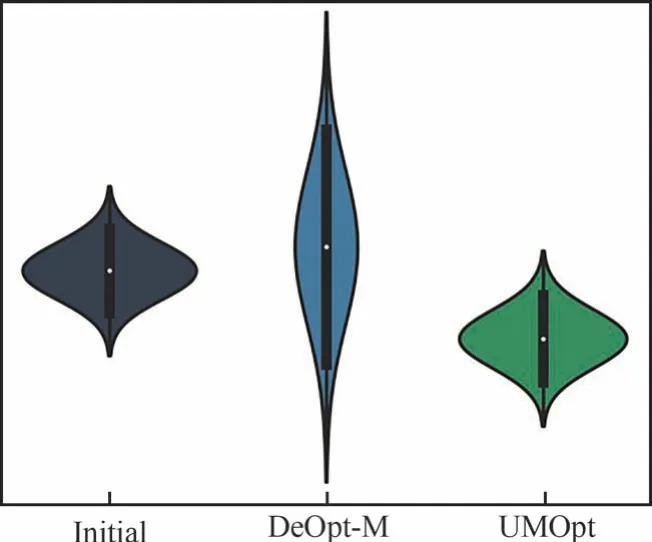
圖29 跨聲速確定性及不確定性優化Fig.29 Random distribution of drag coefficients for transonic deterministic and uncertain optimization

跨聲速確定性和不確定性優化歷程如圖30所示，不確定性優化歷經主迭代8 次，最終滿足約束和目標函數收斂條件。優化歷程中前半程目標函數下降較快，后半程目標函數變化較小，主要完成的是對壓力分布的調整和光順，優化過程中阻力系數標準差變化較小，說明全湍流考慮馬赫數和迎角不確定性的優化僅降低了平均阻力性能，未明顯優化魯棒性。不確定性優化設計主要的優化方向是不斷提高頭部吸力峰值，減小后部的升力載荷，將載荷向前緣移動。

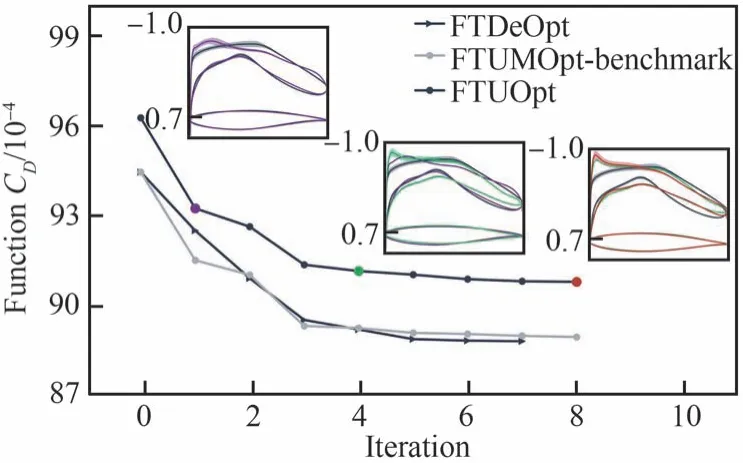
圖30 跨聲速確定性及不確定性優化歷程（黑色圓形線：DeOpt，確定性優化目標函數變化；黑色三角線：UMOpt，不確定性優化目標函數變化；灰色圓形線：UMOpt，不確定性優化中基準流場的阻力系數變化）Fig.30 Transonic deterministic and uncertain optimization history（Black circle line： DeOpt， change of objective function in deterministic optimization；black triangle line： UMOpt， change of objective function in uncertainty optimization； gray circle line： UMOpt， change of drag coefficient of mean flow field in uncertainty optimization）

6 結 論

基于非嵌入式多項式混沌法并結合伴隨方程法建立了高效、可靠的基于梯度算法的不確定性優化設計方法，相關研究總結如下：

1）利用伴隨方程法求得的導數信息發展了一種梯度增強型多項式混沌法，實現了高效精確的不確定性分析。通過亞聲速和跨聲速二維翼型的不確定性分析算例驗證了所使用的梯度增強型多項式混沌法的精度。其可對力系數、空間流場壓力分布的不確定性響應進行較為全面而準確的預測。

2）利用基于方差分解的全局敏感性分析方法對亞聲速和跨聲速二維翼型不確定性分析算例中不確定性變量的敏感性進行量化。結果表明，前后緣的條狀區域常受到馬赫數不確定性的影響，駐點附近的流場壓力系數常受到迎角不確定性的影響。亞聲速狀態下對流場不確定性響應產生主要影響的是迎角；對于存在激波的跨聲速流場，對流場壓力系數標準差貢獻最大的是馬赫數。

3）基于梯度增強型多項式混沌法、FFD 參數化方法、IDW 動網格方法和SNOPT 優化算法搭建了不確定性梯度優化設計框架。利用該框架分別對低亞聲速二維翼型、跨聲速二維翼型進行考慮馬赫數和迎角不確定性的優化設計。

4）優化結果表明，只考慮確定性性能的優化設計有可能導致不確定性條件下性能的降低，而考慮不確定性的優化設計相比于確定性優化設計能夠顯著提高翼型抵抗馬赫數和迎角擾動的能力，同時減小阻力均值和標準差，分別可達到約17%和80%。

研究結論表明，所建立的梯度增強型多項式混沌法以及與伴隨理論耦合的不確定性梯度優化設計系統可以應用于具有大規模確定性設計變量和少量不確定性變量的氣動魯棒優化設計。